隨機(jī)搜索算法在護(hù)理實(shí)習(xí)生排班問(wèn)題中的研究與應(yīng)用

張立，忻凌，王麗，馬忻（.安徽中醫(yī)藥大學(xué)第一附屬醫(yī)院，安徽　3003；.安徽財(cái)貿(mào)職業(yè)學(xué)院，安徽　3007）

隨機(jī)搜索算法在護(hù)理實(shí)習(xí)生排班問(wèn)題中的研究與應(yīng)用

張立1，忻凌1，王麗2，馬忻1
（1.安徽中醫(yī)藥大學(xué)第一附屬醫(yī)院，安徽230031；2.安徽財(cái)貿(mào)職業(yè)學(xué)院，安徽230071）

0　引言

護(hù)理實(shí)習(xí)生排班問(wèn)題是一種典型的組合優(yōu)化問(wèn)題，其目的是對(duì)護(hù)理實(shí)習(xí)生的實(shí)習(xí)期進(jìn)行合理的安排［1］。該問(wèn)題的解決一方面需要滿足實(shí)習(xí)生的要求，安排他們進(jìn)入需要學(xué)習(xí)的科室，實(shí)現(xiàn)實(shí)習(xí)目標(biāo)；另一方面需要滿足實(shí)習(xí)科室的要求，使各科室的實(shí)習(xí)生數(shù)量在周期內(nèi)相對(duì)均衡。高質(zhì)量的排班方案不僅能夠滿足護(hù)理實(shí)習(xí)生的實(shí)習(xí)需求，還能夠保證醫(yī)院各科室正常運(yùn)作。

護(hù)理實(shí)習(xí)生排班問(wèn)題是一種關(guān)于人員日程自動(dòng)編排的問(wèn)題［2］。單個(gè)實(shí)習(xí)生的排班問(wèn)題相對(duì)比較簡(jiǎn)單，但面對(duì)實(shí)習(xí)生數(shù)量相對(duì)龐大，而實(shí)習(xí)科室的承受能力極其有限的實(shí)際情況，實(shí)習(xí)生排班問(wèn)題的求解就變得非常困難。對(duì)于護(hù)理實(shí)習(xí)排班問(wèn)題的研究目前在國(guó)內(nèi)并不廣泛，主要集中在排班方法對(duì)于教學(xué)效果的影響［3-4］上。

傳統(tǒng)的人員日程編排問(wèn)題是將人員的時(shí)間順序看作一條路徑，利用不用長(zhǎng)度的日程進(jìn)行填充，使路徑中的空閑時(shí)長(zhǎng)最短。目前，國(guó)內(nèi)研究者對(duì)人員日程編排問(wèn)題進(jìn)行了廣泛的研究：文獻(xiàn)［5-7］提出了帶約束的護(hù)士排班模型，并使用一系列變換規(guī)則來(lái)求解護(hù)士排班問(wèn)題；王超等［8］對(duì)變領(lǐng)域搜索算法進(jìn)行改進(jìn)，來(lái)解決排班問(wèn)題。此外，一些研究者從管理角度對(duì)人員排班工作進(jìn)行優(yōu)化，陸蕊君等［9-10］通過(guò)調(diào)整班次，重新制定和完善崗位職責(zé)，改進(jìn)排班模式，實(shí)行彈性工作制，在一定程度上解決了人力資源與病人期望不平衡的矛盾及護(hù)士編制不足、護(hù)士班次變換頻繁的問(wèn)題。

護(hù)理實(shí)習(xí)生的排班工作目前仍主要由人工方式完成，工作量很大，而且容易出錯(cuò)，各科室不同時(shí)間人員分布也極不均衡。搜索算法利用計(jì)算機(jī)的高性能窮舉一個(gè)問(wèn)題部分的或所有的可能情況，從而求解出問(wèn)題的解。隨機(jī)搜索算法實(shí)際上是根據(jù)初始條件和擴(kuò)展規(guī)則構(gòu)建一個(gè)解答樹(shù)，解答樹(shù)上的各解結(jié)點(diǎn)隨機(jī)獲得，最終獲得一個(gè)日程編排問(wèn)題的解。隨機(jī)搜索算法能夠有效提高工作效率，避免人工方式產(chǎn)生的錯(cuò)誤，并通過(guò)隨機(jī)過(guò)程在大數(shù)據(jù)的環(huán)境下平衡科室人數(shù)。

本文提出一個(gè)求解護(hù)理實(shí)習(xí)排班的隨機(jī)搜索算法，利用隨機(jī)算法在海量數(shù)據(jù)分配中的優(yōu)勢(shì)，解決排班方案不均衡的問(wèn)題。

1　護(hù)理實(shí)習(xí)生排班模型

1.1模型約束條件

護(hù)理實(shí)習(xí)排班問(wèn)題是指為不同院校的學(xué)生在給定的實(shí)習(xí)時(shí)間段內(nèi)安排實(shí)習(xí)科室，并使該排班方案滿足各種硬性約束條件，同時(shí)盡量滿足各種軟性約束條件。硬性約束條件是指在整個(gè)排班方案中必須要滿足的條件，任何違反硬性約束條件的排班方案都是不可行的；軟性約束條件是在排班方案中希望能夠得到最大滿足的約束。主要的約束條件如下：

（1）硬性約束條件：

①學(xué)生的每個(gè)周次有必須有安排；

②必去科室必須在實(shí)習(xí)期內(nèi)出現(xiàn)；

③回避科室在實(shí)習(xí)期內(nèi)不能出現(xiàn)；

④學(xué)生進(jìn)入非單周實(shí)習(xí)科室實(shí)習(xí)，必須在指定時(shí)間；

⑤同類(lèi)型科室只能去一個(gè)；

⑥各科室的人員安排不得超過(guò)其最大承受人數(shù)；

（2）軟性約束條件：

①實(shí)習(xí)科室的安排每周人數(shù)盡量平穩(wěn)；

②優(yōu)先科室盡量靠前安排；

③某大類(lèi)科室（如內(nèi)科科室或外科科室）可規(guī)定數(shù)量選取（最少去1個(gè)，最多去N個(gè)）；

④科室安排盡量齊整，避免出現(xiàn)斷檔。

上述約束條件是測(cè)試數(shù)據(jù)集中可能出現(xiàn)的約束。對(duì)于某一特定院校的數(shù)據(jù)集來(lái)說(shuō)，并不一定全部出現(xiàn)。因此，這些約束條件能夠較好地反映實(shí)際應(yīng)用的不同要求。

1.2護(hù)理實(shí)習(xí)生排版模型

在本文中，我們將單個(gè)實(shí)習(xí)生的排班模型描述為：從某一個(gè)時(shí)間點(diǎn)開(kāi)始 （實(shí)習(xí)生實(shí)習(xí)期的開(kāi)始時(shí)間），按照一定規(guī)則隨機(jī)選取科室對(duì)時(shí)間序列進(jìn)行填充。其中，各實(shí)習(xí)科室有一下特點(diǎn)：①科室分為1周科室、2周科室和3周科室，實(shí)習(xí)生在其中的實(shí)習(xí)時(shí)間分別為1周、2周和3周，為了便于管理，2周科室和3周科室分別必須在指定的統(tǒng)一時(shí)間安排進(jìn)入；②同類(lèi)科室需要回避，同一實(shí)習(xí)生不能重復(fù)去2個(gè)同類(lèi)型科室，例如手術(shù)室與介入手術(shù)室屬于同類(lèi)科室，腦病1科與腦病2科屬于同類(lèi)科室；③各科室還可分為大類(lèi)科室，如心內(nèi)科、內(nèi)分泌科、消化內(nèi)科等屬于內(nèi)科科室，普外科、骨科、腦外科等屬于外科科室。

下面我們給出一些重要的決策變量和參數(shù)：

我們考慮科室的集合D、實(shí)習(xí)生的集合S和科室負(fù)擔(dān)的集合B。其中科室Di定義為Di（IDi，ki，class1i，class2i，Ni），其中IDi代表科室唯一ID，表示科室屬于幾周科室，class1i表示科室小類(lèi)，用于區(qū)分同類(lèi)型科室，class2i表示科室大類(lèi)，用于區(qū)分大類(lèi)科室，Ni表示科室Di最多可以同時(shí)容納的人數(shù)；實(shí)習(xí)生Si定義為Si（starti，endi，ti），其中starti和endi分別表示實(shí)習(xí)生實(shí)習(xí)的起止時(shí)間，ti表示實(shí)習(xí)生當(dāng)前的時(shí)間戳；科室負(fù)擔(dān)Bij定義為Bij（IDi，tj，mij），其中IDi代表科室唯一ID，tj表示科室當(dāng)前的時(shí)間戳，mij表示科室i在時(shí)間tj的實(shí)際人數(shù)，mij必須滿足約束條件mij≤Ni，即科室的實(shí)際安排人數(shù)不得超過(guò)最大人數(shù)上限。

2　隨機(jī)搜索算法與流程

隨機(jī)搜索算法是指每次從科室的集合中隨機(jī)搜索一個(gè)合適的科室填入實(shí)習(xí)生的時(shí)間序列中，直到所有時(shí)間填滿為止。下面詳細(xì)描述我們給出的隨機(jī)算法：

（1）從實(shí)習(xí)生集合中獲取一個(gè)學(xué)生Si（starti，endi，ti），初始ti=starti。針對(duì)實(shí)習(xí)生的實(shí)習(xí)要求，將科室集合D劃分成必去科室子集D1、回避科室子集D2和其他科室子集D3；

（2）從科室集合中按要求隨機(jī)搜索一個(gè)科室，并驗(yàn)證其是否合適。如果合適，則填入實(shí)習(xí)序列，具體約束如下：

①如果ti%6=0時(shí)，首先從必去科室子集D1中以ki∈｛2，3｝為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從必去科室子集D1中以ki=1為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以ki=1為條件進(jìn)行隨機(jī)抽取；如果仍然無(wú)法滿足，則當(dāng)前時(shí)間戳ti=ti+1，空閑時(shí)間Ti=Ti+1；

②如果ti%3=0時(shí)，首先從必去科室子集D1中以ki=3為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以ki=3為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從必去科室子集D1中以ki=1為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以ki=1為條件進(jìn)行隨機(jī)抽取；如果仍然無(wú)法滿足，則當(dāng)前時(shí)間戳ti=ti+1，空閑時(shí)間Ti=Ti+1；

③如果ti%2=0時(shí)，首先從必去科室子集D1中以ki=2為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其他科室子集D3中以ki=2為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從必去科室子集D1中以ki=1為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以ki=1為條件進(jìn)行隨機(jī)抽取；如果仍然無(wú)法滿足，則當(dāng)前時(shí)間戳ti=ti+1，空閑時(shí)間Ti=Ti+1；

如果ti%3！=0且ti%2！=0時(shí)，首先從必去科室子集D1中以ki=1為條件進(jìn)行隨機(jī)抽取；如果所有科室都無(wú)法滿足硬性約束的要求，則從其它科室子集D3中以ki=1為條件進(jìn)行隨機(jī)抽取；如果仍然無(wú)法滿足，則當(dāng)前時(shí)間戳ti=ti+1，空閑時(shí)間Ti=Ti+1；

⑤插入3周科室時(shí)，必須遵循條件endi-ti+1＞=3；插入2周科室時(shí)，必須遵循條件endi-ti+1＞=2；插入1周科室時(shí)，必須遵循條件endi-ti+1＞=1。

（3）安排科室成功后，則重復(fù)步驟（2），繼續(xù)安排科室，如果ti＞endi，則排班成功，退出循環(huán)。

3　實(shí)驗(yàn)結(jié)果與分析

針對(duì)護(hù)理實(shí)習(xí)生排班問(wèn)題，本文提出了一個(gè)隨機(jī)搜索算法。該算法不僅能夠?qū)崿F(xiàn)護(hù)理實(shí)習(xí)生排班的自動(dòng)化，而且能夠解決科室人數(shù)分布不均衡的問(wèn)題。下一步將對(duì)該算法進(jìn)行實(shí)現(xiàn)，并使用數(shù)據(jù)對(duì)進(jìn)行檢驗(yàn)。

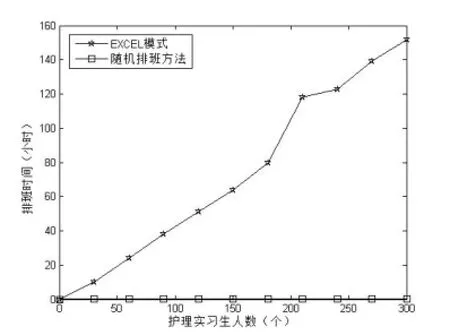
圖1　排班時(shí)間對(duì)比圖

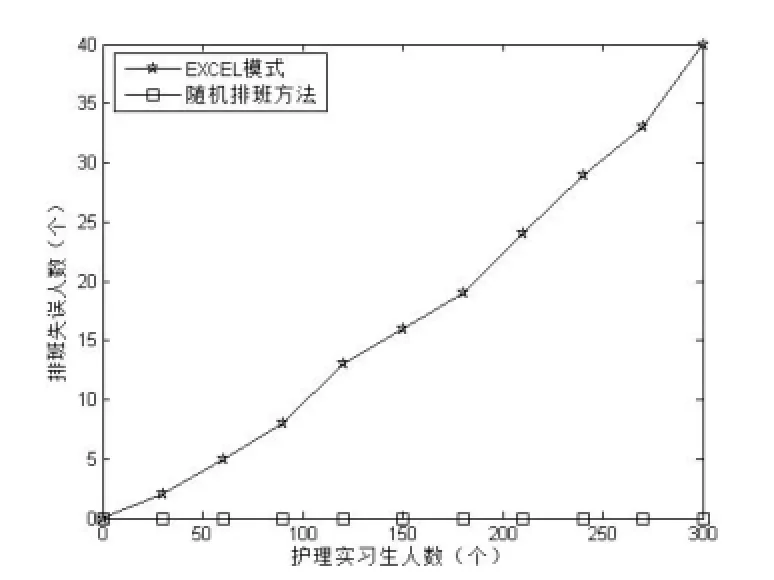
圖2　排班正確率對(duì)比圖

（1）排班效率

本文在人工模式排班累計(jì)統(tǒng)計(jì)了300名護(hù)理實(shí)習(xí)生所消耗的時(shí)間，并對(duì)比了本文實(shí)現(xiàn)同樣人數(shù)的排班所消耗的時(shí)間，對(duì)比結(jié)果如圖1所示。

由圖1，發(fā)現(xiàn)傳統(tǒng)的排班方式在處理這么大人數(shù)的排班消耗的時(shí)間遠(yuǎn)遠(yuǎn)大于本文實(shí)現(xiàn)方法，本文的實(shí)現(xiàn)方法只需要數(shù)分鐘就能一次完成數(shù)百名護(hù)理實(shí)習(xí)生的排班。因此，本文的實(shí)現(xiàn)方法大大地提高了護(hù)理實(shí)習(xí)生排班的效率。

（2）排班正確率

本文搜集了利用傳統(tǒng)的方式排班300名護(hù)理實(shí)習(xí)生的失誤人數(shù)，并對(duì)比了本文的實(shí)現(xiàn)方法，如圖2所示。

由圖2可知，本文的實(shí)現(xiàn)方法的正確率遠(yuǎn)遠(yuǎn)高于傳統(tǒng)的排班方式。同樣，證明了本文的實(shí)現(xiàn)方法的穩(wěn)定性。

（3）排班均衡問(wèn)題

關(guān)于排班均衡的問(wèn)題，并沒(méi)有一個(gè)嚴(yán)格的標(biāo)準(zhǔn)來(lái)衡量，但從本文方法實(shí)施之后的反饋來(lái)說(shuō)，科室的護(hù)理實(shí)習(xí)生基本上達(dá)到均衡，護(hù)理實(shí)習(xí)生實(shí)習(xí)的科室也比以前豐富，而且實(shí)習(xí)的效果也比以前好。這側(cè)面反映了本文實(shí)現(xiàn)方法基本上解決了排班不均衡的問(wèn)題。

4　結(jié)語(yǔ)

本文根據(jù)護(hù)理實(shí)習(xí)的約束條件提出了護(hù)理實(shí)習(xí)生的排班模型，并將隨機(jī)搜索算法應(yīng)用到護(hù)理實(shí)習(xí)生的排班中，實(shí)驗(yàn)結(jié)果表明本文的護(hù)理實(shí)習(xí)生的排班相比較于傳統(tǒng)的排班模式，在排班效率、排班的準(zhǔn)確率上都有很明顯的提升，并解決了排班的均衡問(wèn)題。但本文的方案是針對(duì)于護(hù)理實(shí)習(xí)生的排班，對(duì)于其他護(hù)士的排班是否有同樣的效果并沒(méi)有驗(yàn)證，因此，本文的下一步研究方向是提出針對(duì)所有護(hù)理人員的排班實(shí)現(xiàn)與改進(jìn)。

［1］謝屹紅.護(hù)士排班方式與護(hù)理人力資源的合理利用［J］.中國(guó)實(shí)用護(hù)理雜志，2004，20（4）：65-65.

［2］BRUCKER P，QU R，BURKE E.Personnel scheduling：models and complexity［J］.European Journal of Operational Research，2011.467-473.

［3］黎建敏，林婉萍.APN排班工作職責(zé)作為實(shí)習(xí)目標(biāo)的臨床護(hù)理教學(xué)效果初探［J］.國(guó)際醫(yī)藥衛(wèi)生導(dǎo)報(bào)，2011，17（1）：120-122.

［4］史愛(ài)玲等.一對(duì)一帶教與排班制帶教在護(hù)理實(shí)習(xí)生中的教學(xué)效果比較［J］.齊魯護(hù)理雜志，2014，（8）：12-13.

［5］沈吟東，陳名暉，鄧婕.利用矩陣向量化變換求解護(hù)士排班問(wèn)題［C］.中國(guó)控制與決策會(huì)議論文集，2008：1019-1022.

［6］柯彩霞，謝文，劉曉華，等.護(hù)士排班模式改革與效果［J］.中國(guó)護(hù)理管理，2008，8（11）：38-40.

［7］馮艮嬌，盧海濤.護(hù)理排班模式改革探討［J］.南方護(hù)理學(xué)報(bào)，2002，9（4）：67-68.

［8］王超，董興業(yè).求解護(hù)士排班問(wèn)題的變領(lǐng)域搜索算法［J］.計(jì)算機(jī)應(yīng)用，2013，33（2）：338-341，352.

［9］陸蕊君，鮑學(xué)英，王惠芬.護(hù)士排班方法的改進(jìn)與實(shí)踐［J］.當(dāng)代護(hù)士：綜合版，2007（2）：23-23.

［10］唐富琴，張琳.人性化管理在護(hù)士排班中的運(yùn)用［J］.護(hù)理學(xué)報(bào)，2009，16（16）：18-19.

張立，男，安徽合肥人，初級(jí)工程師，研究方向?yàn)橛?jì)算機(jī)技術(shù)

忻凌，男，安徽合肥人，工程師，研究方向?yàn)槿斯ぶ悄?/p>

馬忻，女，安徽合肥人，副教授，研究方向?yàn)樽o(hù)理學(xué)及其管理

王麗，女，安徽合肥人，講師，研究方向?yàn)樾畔⒐芾?/p>

Nursing Practice；Random Algorithm；Scheduling

Research and Application of Stochastic Search Algorithm in the Scheduling Problem of Nursing Interns

ZHANG Li1，XIN Ling1，WANG Li2，MA Xin1
（1.The First Afflicted Hospital of Anhui University of TCM，Anhui 230031；2.Anhui Finance&Trade Vocational College，Anhui 230071）

1007-1423（2015）23-0035-04

10.3969/j.issn.1007-1423.2015.23.008

2015-05-12

2015-08-05

臨床護(hù)理教學(xué)是各教學(xué)醫(yī)院的一項(xiàng)重要工作。目前，各醫(yī)院多采用人工方式完成護(hù)理實(shí)習(xí)生排班工作，但由于實(shí)習(xí)生數(shù)量較大、進(jìn)崗時(shí)間不一、實(shí)習(xí)大綱要求復(fù)雜等原因，使實(shí)習(xí)生排班工作出現(xiàn)工作量大、易出錯(cuò)、科室分配不均衡等問(wèn)題。提出將隨機(jī)搜索算法應(yīng)用在護(hù)理實(shí)習(xí)生排班中，并從排班效率、排班正確率以及排班均衡問(wèn)題上對(duì)比傳統(tǒng)的排班方式。實(shí)驗(yàn)結(jié)果表明：將隨機(jī)搜索算法應(yīng)用于護(hù)理實(shí)習(xí)生排班中，發(fā)現(xiàn)排班效率、排班準(zhǔn)確率高，而且可避免排班不均衡的問(wèn)題。

護(hù)理實(shí)習(xí)；隨機(jī)算法；排班

安徽中醫(yī)藥大學(xué)臨床科研基金（No.2012LC1-026B）

The clinical nursing teaching is an important task in the teaching hospitals.At present，most hospitals manually finish scheduling work of nursing interns，but with large quantities of interns，different time of punching in the post，complex requirements of guideline for internship and other reasons，there are many problems existed in the scheduling work，such as heavy workload，error-prone problems，and the uneven distribution of the department.Presents the random search algorithm applied in nursing interns scheduling，and makes comparison with traditional scheduling methods in view of the efficiency，accuracy and equilibrium of scheduling.The experimental results show that，when the random search algorithms is applied to the nursing trainee scheduling，efficiency and accuracy rate are higher，and the problem of unbalanced scheduling are avoided as well.