基于滑窗置信傳播算法的聯合信源信道編碼
鹿增輝,方 勇,霍迎秋
(西北農林科技大學 信息工程學院,陜西 楊凌 712100)
基于滑窗置信傳播算法的聯合信源信道編碼
鹿增輝,方 勇,霍迎秋
(西北農林科技大學 信息工程學院,陜西 楊凌 712100)
針對聯合信源信道編碼中信源統計特性和信道噪聲參數未知情況下,解碼算法性能急劇下降的問題,提出一種基于滑窗置信傳播算法(SWBP)的聯合信源信道編碼,簡稱滑窗算法。研究采用不規則重復累積(IRA)碼來實現基于滑窗置信傳播算法的聯合信源信道編碼,IRA碼可以取得與低密度奇偶校驗(LDPC)碼同樣優越的性能,但編碼復雜度遠遠低于LDPC碼。在解碼端引入滑動窗口,通過實時地估計不斷變化的信源統計特性和信道噪聲參數,從而提高解碼速率。實驗結果表明該算法具有接近相關參數已知情況下的理想性能、不依賴于初始參數、復雜度低且易于實現等優點。
聯合信源信道編碼;不規則重復累積碼;置信傳播;相關參數估計;低密度奇偶校驗碼
通信的目的是實現消息從信源到信宿的可靠傳輸,該過程一般需要進行信源編碼和信道編碼。信源編碼的主要目的是提高碼字序列中碼元的平均信息量,即去除消息中的冗余,提高傳輸效率。信道編碼的目的在于提高系統的可靠性,通過增加冗余位和校驗信息,使系統具有一定的糾錯能力和抗干擾能力,從而極大地避免碼流傳送中誤碼的發生[1]。在香農信源信道分離理論的指導下,通常信源編碼和信道編碼分離開來進行獨立地編解碼[2]。然而,在許多場景下,獨立編碼已經不能滿足實際的需求,例如:受資源限制的系統、時變系統和多用戶系統等,因此聯合信源信道編碼逐漸成為當前的研究熱點之一。通常聯合信源信道編碼有如下幾種實現方案:分層編碼[3]、基于低密度奇偶校驗(Low Density Parity Check, LDPC)碼的聯合譯碼[4]、Turbo碼[5]和多描述編碼[6]。不規則重復累積碼(Irregular Repeat Accumulate, IRA)是一種特殊的LDPC碼,不僅可以實現對信源的壓縮,而且可以進行信道容錯,因此本文中采用IRA碼來實現聯合信源信道編碼[7]。
在IRA碼譯碼算法中,對信源統計特性和信道噪聲相關參數的估計,仍是影響解碼算法性能的重要因素[8]。為了提高解碼效率,學者們提出了許多參數估計方法。鄭思明等人提出基于粒子濾波的置信傳播算法[9],該方法在標準置信傳播算法基礎上引入粒子濾波的過程,通過為每個變量節點賦予不同權重的隨機粒子,然后在每次標準置信傳播譯碼之后,重新計算粒子的置信和權重,舍棄權重較小的粒子,保留權重大的粒子,以實現對信源后驗概率的估計。方勇提出基于滑窗的置信傳播(Belief Propagation,BP)算法[10],該算法的主要思想是在解碼端引入滑動窗口,在每輪置信傳播算法迭代之后,不斷地對信源參數進行估計和更新,從而提高譯碼算法性能。
鑒于上述研究是基于理想信道進行的缺點,本文在IRA聯合譯碼算法的基礎上提出一種改進的IRA聯合譯碼算法,即基于滑窗置信傳播算法的聯合信源信道編碼。改進的IRA聯合譯碼算法基于標準聯合譯碼算法基礎上引入滑動窗口,解碼的同時對信源似然概率信息和信道噪聲似然信息進行實時估計,從而極大地提高解碼速率。改進的IRA聯合譯碼算法具有時間復雜度低,對初始值不敏感等優點。
1 基于IRA碼的聯合信源信道編碼
傳統的聯合信源信道編碼,首先使用信源碼對信源進行壓縮,再串連一個信道碼以實現信道容錯。本文采用一種特殊的LDPC碼,即IRA碼。它既可以實現信源壓縮,又可以實現信道容錯,非常適合聯合信源信道編碼的應用場景。
1.1 系統模型與描述
如圖1所示,利用在解碼器中引入一個內嵌編碼器的方法可以將分布式編碼轉化為傳統編碼[11],如圖1所示。具體轉換過程如下:sx=Hx,其中sx為x的伴隨式,H為奇偶校驗矩陣。在解碼端,首先計算邊信息y的伴隨式sy=Hy,則s=sx⊕sy=H(x⊕y)=Hz。此時,可以將信源x和邊信息y之間交叉概率的估計問題轉換為求z統計特性參數。

圖1 解碼器中引入內嵌編碼器模型
1.2 基于IRA的編碼器和解碼器
圖2所示為IRA碼的二分圖表示,IRA碼有變量節點和校驗節點[12]。[x1,x2,…,xn]和[u1,u2,…,um]代表變量節點,[s1,s2,…,sm]表示校驗節點。

圖2 IRA碼二分圖表示
基于IRA碼的聯合信源信道編碼的原理可描述如下[13]:
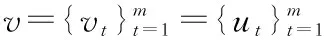

(1)
再通過IRA譯碼算法進行解碼,就可以恢復信源x和u。
上述過程可以總結為:兩邊的變量節點,將置信度傳遞給中間校驗節點。然后中間的校驗節點,再將自身置的信度分別傳遞給兩邊的變量節點。此過程不斷迭代,直至譯碼成功或達到最大迭代次數。實際上,x到s的過程為壓縮,從s到u是一個容錯過程。
2 改進的IRA聯合譯碼算法
在信源統計特性和信道噪聲參數未知的情況下,為了解決IRA聯合譯碼算法性能急劇下降的問題,本文基于滑窗置信傳播算法提出改進的IRA聯合譯碼算法,以下簡稱滑窗置信傳播算法。下面分別從滑窗置信傳播算法的流程、改進后的譯碼算法和參數估計三方面對改進后的算法進行介紹。
2.1 符號說明



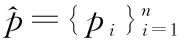

Li:與變量節點xi相連的所有校驗節點的索引集合;
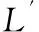
Mj:與校驗節點sj相連的變量節點xi的索引集合;
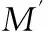
αij:xi傳遞給sj的消息;
αkj:uk傳遞給sj的消息;
βji:sj傳遞給xi的消息;
βjk:sj傳遞給uk的消息。
2.2 算法流程圖
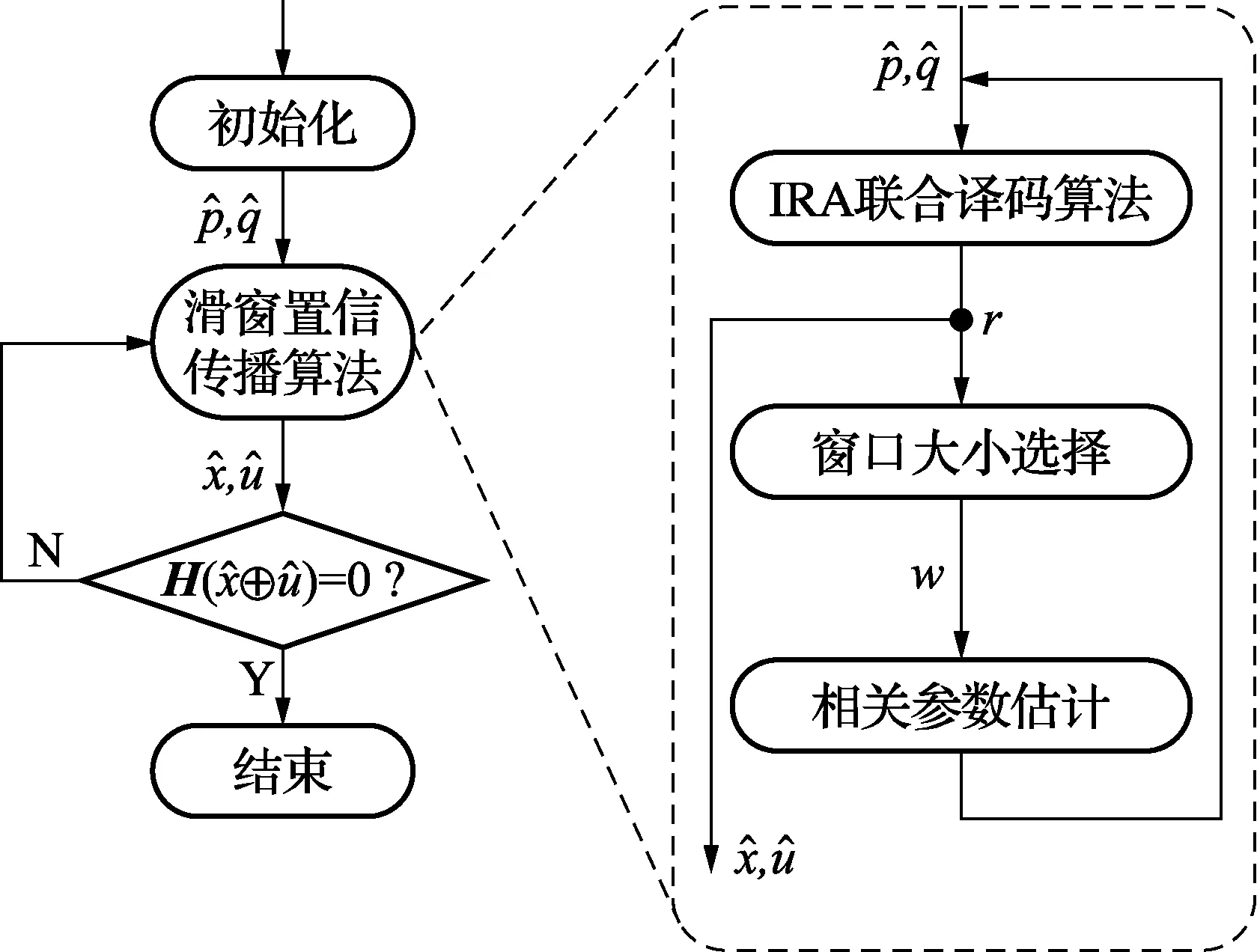
圖3 SWBP算法流程圖
2.3 IRA聯合譯碼算法
標準的IRA聯合譯碼算法,包含如下4步:
1) 變量節點向校驗節點傳遞消息
(2)
2) 校驗節點向變量節點傳遞消息
(3)
3) 計算后驗概率
(4)
4) 硬判決譯碼
(5)
2.4 參數估計
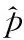
1)信源統計特性的估計
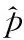
(6)
(7)
2)信道噪聲參數的估計
類似于對信源統計特性的估計,對于信道噪聲參數的估計,同樣使用滑窗技術。估計公式如下
(8)
3 窗口大小的確定
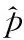
3.1 自適應窗口大小算法描述
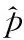
(9)
(10)
則該問題可轉化為
(11)
(12)
3.2 搜索策略
在尋找最優窗口大小時,不需要從1到n搜索每個奇數。一方面,窗口太大或太小時該算法的性能都不會太好。另一方面,相鄰兩個窗口的大小對算法性能影響差別不大。因此,可采取間隔一個距離的方法進行搜索,假設間隔為20,則分別搜索大小為21、41、61等窗口。
4 實驗結果
實驗采用IRA碼仿真滑窗算法的譯碼性能及其參數估計能力。對實驗中的參數做如下說明:假設信源的統計特性取值為正弦函數,即pi=p+(p-0.01)×sin(2πi/n)。假設信道的噪聲參數也取值正弦函數,即qk=q+(q-0.01)×sin(2πk/m)。使用碼長為6 336的規則碼,交叉測試6種不同的速率,即q取值0.05時,p分別取值0.02,0.03,0.04,0.05,0.06,0.07;p取值0.04時,q分別取值0.02,0.03,0.04,0.05,0.06,0.07。
表1描述了碼長為6 336的規則IRA碼,當q取0.05時,信源統計特性p在6種不同速率下的譯碼性能。其中ideal列表示在已知非平穩信源的統計特性的條件下,IRA碼獲得的實際編碼速率;static列表示將非平穩信源看成平穩信源,且使用p來初始化變量節點的置信度,獲得的實際編碼速率;swbp-p列表示在不知道平穩信源的統計特性條件下,使用p來初始化變量節點置信度,運行SWBP算法獲得的編碼速率。同理swbp-2p、swbp-0.5p列是分別使用2p和0.5p初始化置信度獲得的編碼速率。

表1 q為0.05時、p在6種不同碼率下的譯碼性能
從表1的實驗結果可以看出,在信源統計特性未知的前提下,SWBP算法的性能接近于已知信源統計特性的理論性能,即ideal列與swbp-p列非常接近。主要是因為SWBP算法在迭代譯碼的過程中不斷地對非平穩信源的統計特性和噪音參數進行估計與更新。swbp-p列、swbp-2p列和swbp-0.5p列實驗結果非常接近,這說明對于不同初始化參數p、2p和0.5p對SWBP算法影響不大,因此,該算法具有魯棒性,其性能曲線如圖4所示。
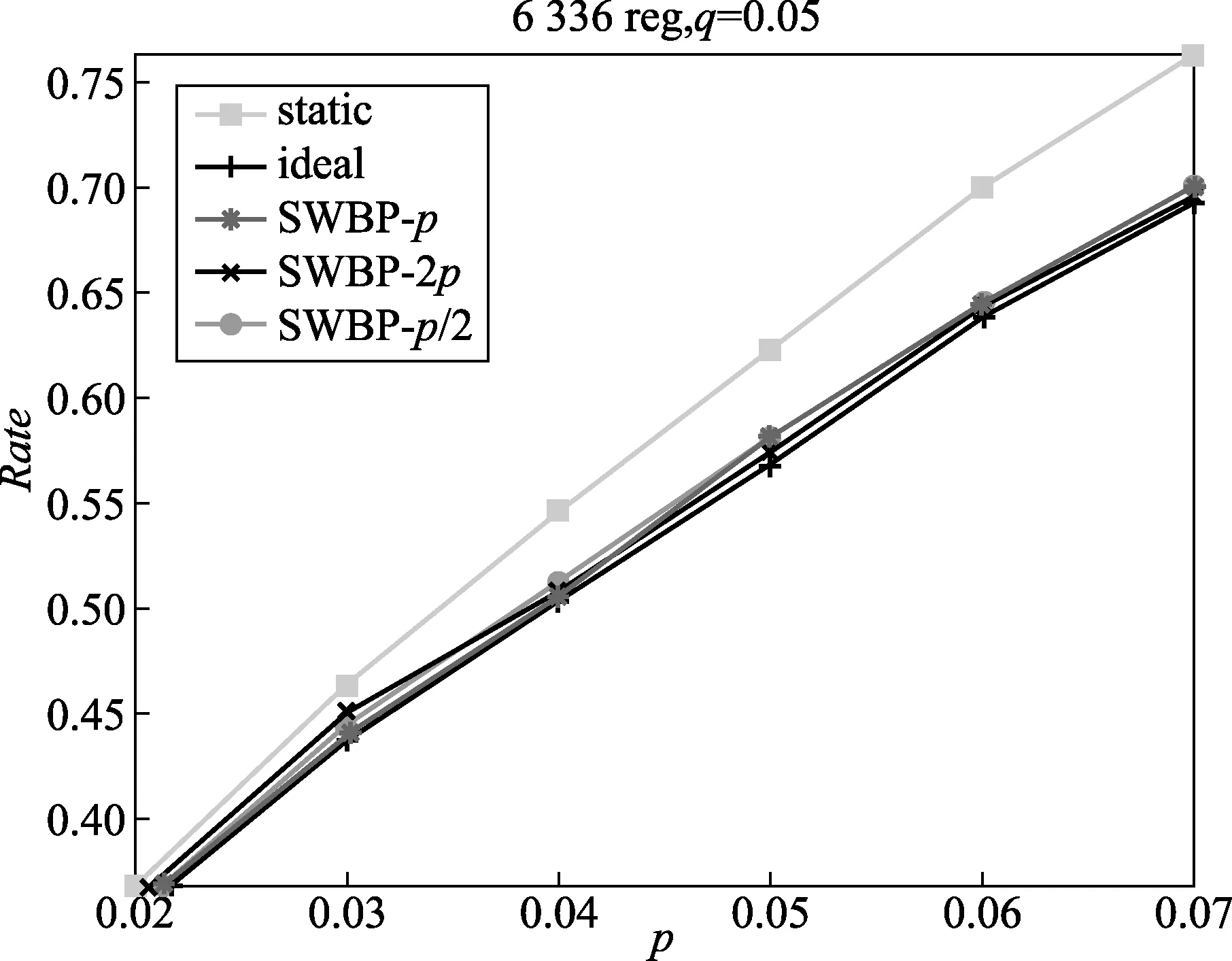
圖4 p在6種不同速率下的譯碼性能
表2描述了碼長為6 336的規則IRA碼,當p取0.04時,信道噪聲參數q在6種不同速率下的譯碼性能。其中ideal列表示在已知信道噪聲參數的條件下,IRA碼獲得的實際編碼速率;static列表示將信道噪聲看成平穩變化的,且使用q來初始化置信度,所獲得的實際編碼速率;swbp-q列表示在未知信道噪聲參數條件下,使用q來初始化置信度,運行SWBP算法獲得的編碼速率。同理swbp-2q、swbp-0.5q列分別表示使用2q和0.5q初始化置信度獲得的編碼速率。
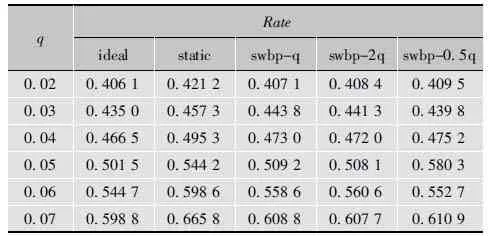
表2 p為0.04時q在6種不同碼率下的譯碼性能
從表2的實驗結果可以看出,在信道噪聲參數未知的前提下,SWBP算法的性能接近于已知信道噪音參數的理論性能,即ideal列與swbp-q列非常接近。這主要是因為SWBP算法在迭代譯碼的過程中不僅可以估計信源的統計特性還可以估計信道的噪聲參數。swbp-q列、swbp-2q列和swbp-0.5q列實驗結果非常接近,這說明SWBP算法對于不同初始化參數q、2q和0.5q不敏感,具有魯棒性,其性能曲線如圖5所示。
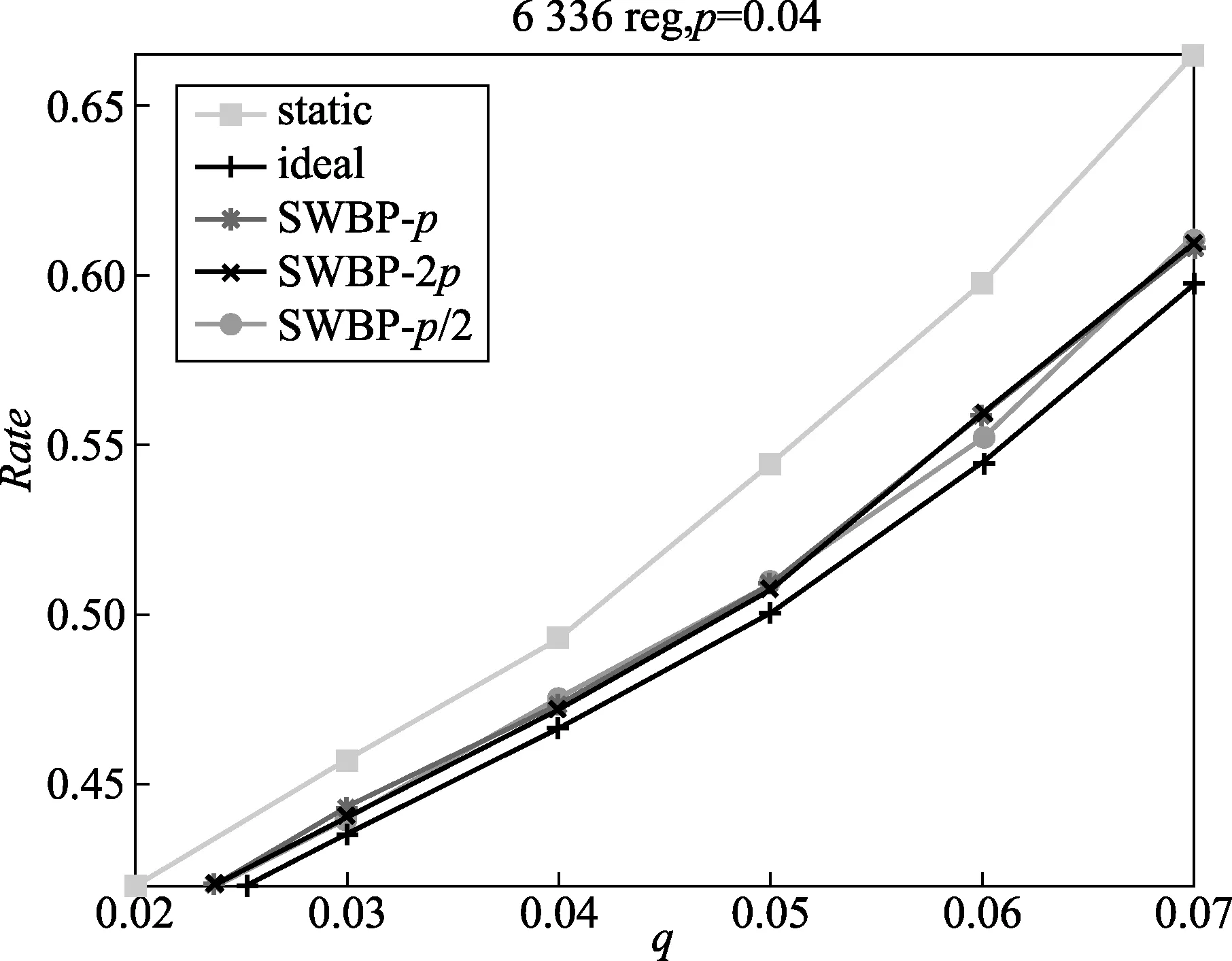
圖5 q在6種不同速率下的譯碼性能
5 結束語
本文提出了一種基于SWBP的聯合信源信道編碼方法,其主要思想是在譯碼階段引入滑窗算法,不斷對信源統計特性和信道噪聲參數進行估計和更新,從而提高了譯碼性能。該方法有效地解決了在譯碼階段信源統計特性和信道噪聲參數未知的情況下,譯碼性能急劇下降的問題。本實驗采用的信源統計特性服從正弦函數,由于滑窗算法對當前變量節點局部統計特性的估計依賴于其周圍變量節點的置信度,因此該方法對其他連續非平穩信源同樣適用。實驗結果表明,該方法的性能接近于理想情況下的性能,具有簡單易實現、時間復雜度低和不依賴于初始值等優點。
[1] 陳運. 信息論與編碼[M]. 2版.北京:電子工業出版社,2011.
[2] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal,1948(27):379-423.
[3] 席志紅,肖春麗,劉曉慧. 基于ROI圖像傳輸的聯合信源信道編碼的研究[J]. 應用科技,2008,35(11):11-14.
[4] 趙旦峰,王詩力,周相超. 基于隱馬爾科夫模型的多元LDPC聯合譯碼[J]. 電子科學,2013,26(8):4-6.
[5] 賈鎮澤,馬林華,張嵩,等. RS碼與LDPC碼的聯合迭代譯碼[J].電視技術,2013,37(17):200-203.
[6] 張丹,李曉峰,簡沖,等. 一種多參數優化的聯合信源信道編碼方法[J].計算機應用研究,2010,27(4):1530-1533.
[7] 袁基睿,陳賀新,趙巖. 基于H.264和Turbo碼的信源信道聯合解碼[J].吉林大學學報:工學版,2007,37(5):1187-1191.
[8] 余華,曹維娜,趙力,等. 信源信道聯合編碼技術用于AVS傳輸的研究[J]. 電視技術,2007,31(8):9-10.
[9] XU Q, STANKOVIC V, XIONG Z. Layered Wyner-Ziv video coding for transmission over unreliable channels[J]. Signal Processing,2006,86(11): 3212-3225.
[10] FANF Yong. Analysis on crossover probability estimation using LDPC syndrome[J]. Science China: Information Sciences,2011,54(9):1895-1904.
[11] WANG S,CUI L,CHENG S,et al. Noise adaptive LDPC decoding using particle filtering[J]. IEEE Trans. Commun.,2011,59(4):913-916.
[12] FANG Yong. LDPC-based lossless compression of nonstationary binary sources using sliding-window belief propagation[J]. IEEE Trans. Communications,2012,60(11):3161-3166.
[13] FANG Yong. Crossover probability estimation using mean-intrinsic- LLR of LDPC syndrome[J]. IEEE Commun. Lett.,2009,13(9): 679-681.
[14] 周勝源,曹治政,臧嵐,等.不規則LDPC碼度分布的優化設計研究[J]. 電視技術,2012,36(15):90-93.
[15] FANG Yong. Joint source-channel estimation using accumulated LDPC syndrome[J]. IEEE Commun. Lett. 2010,14(11):1044-1046.
鹿增輝(1990— ),碩士生,主研信源信道編碼方向的研究;
方 勇(1979— ),教授,博士生導師,主要從事編碼理論、網絡信息論、圖像壓縮與傳輸、并行計算等方向的研究,為本文通訊作者。
責任編輯:時 雯
Joint Source-channel Coding Based on Sliding-window Belief Propagation
LU Zenghui,FANG Yong, HUO Yingqiu
(CollegeofInformationEngineering,NorthwestA&FUniversity,ShaanxiYangling712100,China)
To solve the problem of unknown source statistical properties and channel noise parameters and that of the decoding performance degradation, a new joint source-channel coding scheme based on the Sliding-Window Belief Propagation (SWBP) algorithm is proposed. In this paper, irregular repeat accumulate (IRA) is adopted to achieve the SWBP algorithm in joint source-channel coding. IRA coding can obtain the same superior performance with low density parity check (LDPC) coding, but less than complexity. A sliding-window is introduced in the decoder, and the decoding rate is improved by estimating the changing source statistical properties and channel noise parameters real-timely. The experiment results show that the performance of the proposed algorithm is close to the ideal curve when correlation parameters have been given. While the algorithm shows other advantages, including the robustness to initial parameters, the low linear time complexity, and easy to implement.
joint source-channel coding; irregular repeat accumulate coding; belief propagation; correlation estimation; low density parity check coding
【本文獻信息】鹿增輝,方勇,霍迎秋.基于滑窗置信傳播算法的聯合信源信道編碼[J].電視技術,2015,39(11).
國家自然科學基金項目(61271280);中央高校基本科研業務項目(QN2013086)
TN911.2
A
10.16280/j.videoe.2015.11.023
2015-01-19

