模糊集對分析在礦山采空區穩定性評價中的應用

劉浪，陳忠強

?

模糊集對分析在礦山采空區穩定性評價中的應用

劉浪1, 2，陳忠強3

(1. 西安科技大學能源學院，陜西西安，710054；2. 西部礦井開采及災害防治教育部重點實驗室，陜西西安，710054；3. 北京礦冶研究總院，北京，100070)

針對地下礦山采空區失穩易造成人員傷亡與財產損失而采空區穩定性難以預判的情況，利用模糊集對分析對采空區進行穩定性評價。綜合考慮采空區面積、地應力、支護方式、圍巖質量4種采空區穩定性影響因素，將12個樣本采空區穩定性分為3級，利用模糊隸屬關系計算采空區對應于各指標因素的聯系度，并結合各指標權重，得到各采空區綜合聯系度，利用置信度準則對各采空區穩定性進行評價。研究結果表明：該方法可對采空區穩定性進行預判，并提出相應的維穩對策，采空區穩定性破壞率降低50%左右，同時采空區維穩成本降低約30%。

采空區；穩定性；模糊；集對分析

采空區是地下礦山直接開采原礦的工作面，采空區失穩破壞可能會造成資源損失、損壞暴露在空區之下的機械設備材料，傷害在采場中工作的人員，進而影響礦山的安全生產與經濟效益。一直以來，對礦山采空區的防范與處理都是采礦工作者們研究的重點。然而，采空區失穩的影響因素較多，既有采空區圍巖不穩和臨近區域的擾動干擾等外部因素，又有采空區面積過大和采空區埋深過深等內部因素，影響機制復雜，且各因素量綱也不同，因而難以利用這些因素對采空區穩定性進行量化分析，這也是現階段采空區穩定性研究的一大難點。現階段用來對采空區穩定性評價的手段主要有計算機軟件的數值模擬分析以及以系統工程等數學理論為基礎的系統建模分析[1?3]。計算機數值模擬分析依靠數值模擬軟件對采空區穩定或失穩過程進行動態分析模擬，其優點在于可從時空關系上揭示采空區穩定或失穩變形的過程，直觀甚至動態地演示各影響因素對采空區穩定性的影響情況。但數值模擬分析往往以諸多假定條件為前提，這些假定條件雖然給采空區數值模擬分析帶來了方便，卻也造成數值模擬分析與采空區現場環境的較大差異，而數值模擬恰恰要客觀真實地模擬采空區穩定或失穩的真實情形，因此，數值模擬分析方法一直難以在現場實踐中得到應用。而數學建模分析方法雖無法動態直觀地反映采空區變形乃至失穩破壞的過程，但該方法邏輯嚴謹，計算準確，過程科學合理，結果也較可靠，最重要的是數學建模分析方法能夠對采空區穩定性最終狀態進行判定即預判，因此，可以對采空區失穩進行及早防范，從而能夠減輕礦山的資源損失和經濟損失。基于模糊集對分析的采空區穩定性評價，正是對采空區穩定性進行預判的一種數學分析方法。普通集對分析[4?5]的核心思想是對不確定性系統中2個彼此關聯的集合的特性進行同一性、差異性與對立性分析，然后建立聯系度，通過聯系度對集合間的關系進行最終判定。相對于相關系數，隸屬度及灰色關聯度等靜態分析方法，集對分析的聯系度是一種動態分析方法，能清晰地反映現實集合間的關系結構，且能形象定量對比和揭示集合復雜關系中3種及3種以上的不同秉性。模糊集對分析[6]是針對一般集對分析只能處理邊界確定的分級標準及無法對邊界模糊問題進行處理的缺點而提出的方法，引入模糊數學對邊界模糊問題進行分析。相對于一般的集對分析方法，模糊集對分析考慮了等級邊界的模糊性以及各指標因素的權重，有效避免了差異不確定分量系數的取值，評價結論也更加穩定、合理[7?9]。因此，模糊集對分析比一般集對分析考慮得更加全面，應用范圍也更廣泛。

1 系統建模

1.1 集對分析基本理論

集對分析是以集對及其聯系度的基本概念，刻畫和研究系統中廣泛存在的確定性與不確定性及其轉化規律的一種系統分析技術，它先對不確定系統中2個有關聯的集合與構造集對(如物質與能源、信息與智能等)構成集對(,)，用μ表示其聯系度。

或

(2)

式中：為集合和的表征特性數；為集合和所共同具有的表征特性數；為集合和中相對立的表征特性數；為集合和既不共同具有、又不相互對立的表征特性數；++=；，和為非負實數，且，和需滿足歸一化條件++=1；=/，為同一度，表示集對的同一程度；=/，為差異度，表示集對差異的不確定程度；=/，為對立度，表示集對的對立程度；為差異不確定系數，在[?1,1]內取值，有時也僅起標記作用；為對立度系數，=?1。與對聯系度的作用正好相反。

當在[?1,1]變化時，反映了和2個集合的同一和對立度。當聯系度= 1時，說明和2個集合完全同一，意味著被評價對象與理想狀態完全一致，具備達標條件；當聯系度=?1，說明和2個集合完全對立，不能滿足目標要求。

1.2 模糊集對分析模型

1.2.1 采空區穩定性評價體系

考慮到影響采空區穩定性的外部因素與自身因素[10?13]，并結合礦山的具體實際情況加以歸納，本模型選取以下因素作為采空區穩定性的主要影響因素。

1) 采空區暴露面積。采空區開挖為采空區頂板產生位移，進而破壞提供了空間。采空區暴露面積越大，頂板位移也越大，采空區越容易失穩破壞。

2) 地應力。地應力是造成采空區失穩破壞的主要外部因素，也是采空區產生空間變形及破壞的根本原因。地應力主要由構造應力與自重應力構成，采空區所受的地應力越大，空間變形也越大，就越容易失穩破壞。

3) 支護方式。采空區支護方式對采空區穩定性有重要影響，由于支護方式合理性無法得到直接量化分析，因此，對支護方式采用專家評分法進行評價，評分越高，支護方式越合理，采空區的穩定性越好。

4) 圍巖質量。圍巖質量是對工程巖體諸多因素的1個綜合評價，它綜合了巖石單軸抗壓強度、巖體節理情況、巖體風化情況以及其他水文地質情況等對采空區穩定性有影響的水文地質評價指標。在礦山實際工程中，通常采用BQ分級法、Q系統分級法或南非RMR分級法等對礦山圍巖質量進行分級評價，顯然，圍巖質量越差，采空區頂板位移也就越大，采空區也就越趨向失穩破壞。

1.2.2 聯系度構建

對于穩定性待評價的采空區作為樣本集，將影響采空區穩定的第個影響指標x(=1, 2, …,；為評價指標數，此處=4)看成是1個集合A，將該指標的第級評價標準看成另1個集合B(=1, 2, …,，為評價等級數)，則A與B構成1個集對(A,B)，將指標=1時的第1級評價標準1選取為同、異、反的聯系度計算參照標準，集對(A,B)變為集對(A,1)，其元聯系度為

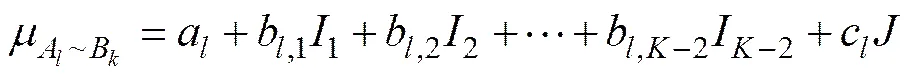
式中：a為x隸屬于1級標準的可能性；b1為x隸屬于2級標準的可能性；b2為x隸屬于3級標準的可能性；b?2為x隸屬于?1級標準的可能性；c為x隸屬于級標準的可能性。

對于越小越優指標(即反向指標)，當＞2時，集對(A,1)的元聯系度為：

(4)

或

(5)

對于式(4)，1≤2≤…≤S?1。當=2時，則集對(A,1)的2元聯系度為

對于式(5)，0≤1≤2，當0與2無確定值時，0=0，2=+∞。針對越大越優指標(即正向指標)，當＞2時，集對(A,1)的元聯系度為

(7)

式中：0≥1≥2。當0與2無確定值時，0=+∞，2=0。

模糊隸屬關系確定聯系度的示意圖如圖1(以5元聯系度為例)所示。

圖1 基于模糊隸屬關系的聯系度計算

1.2.3 指標權重計算

對于模糊集對分析法而言，各指標權重的計算是1項重要工作，它直接關系到最終的各采空區穩定性的評級。確定指標權重的方法有很多，在實際工作中較常見的有統計平均法、變異系數法和層次分析法。變異系數法是直接利用各項指標所包含的信息，通過計算得指標的權重，是一種客觀賦權的方法，完全擺脫了人為因素的干擾。

變異系數法根據各指標的作用大小不同來確定權重，在該評價指標體系中，指標取值差異越大的指標，也就是越難以實現的指標，這樣的指標更能反映被評價單位(影響比重)的差距[14?16]，其計算公式為

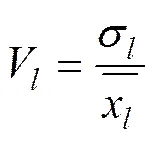
式中：V為第項指標的變異系數，也稱為標準差系數；是第項指標的標準差；為第項指標的平均數。

各項指標的權重w為

1.2.4 綜合聯系度計算

以各指標的1級評價等級標準作為參照，計算綜合聯系度的計算過程如下：對于采空區穩定性評價樣本集合，所有指標l級評價等級標準為，則集對(,)的元聯系度可定義為

(10)

其中：1可理解為采空區穩定性隸屬于1級的可能性；2為采空區穩定性隸屬于2級的可能性；3為采空區穩定性隸屬于3級的可能性；f?1為采空區穩定性隸屬于?1級的可能性；f為采空區穩定性隸屬于級的可能性。

1.2.5 采空區穩定性判定

采空區穩定性的判定可采用最大可能性準則及置信度準則。由于利用最大可能性準則進行采空區穩定性判定時，其最大隸屬值有可能小于0.5，此時隸屬于其他等級的可能性反而比最大隸屬值所屬的等級高。因此，為科學地對采空區穩定性進行判定，采用置信度準則進行采空區穩定性的判定。

先確定置信度，當有某一等級，使

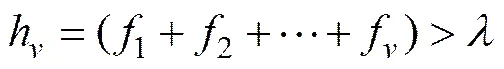
據此，可判定采空區穩定性屬于級。對于置信度的取值，若取值過大則評價結果趨于保守，若取值過小則可能使評價結果的可靠性降低，一般而言∈[0.50，0.70]。基于模糊集對方法的采空區穩定性評價流程如圖2所示。

圖2 系統建模流程

Fig. 2 Flowchart of system model

2 系統建模

2.1 背景簡介

某市位于某一成礦帶上，有十幾家地下礦山，由于水文地質條件復雜，圍巖質量不佳，導致該市礦山在開采過程中，采空區冒落、垮塌等事故時常發生，造成人員傷亡和較嚴重的經濟損失。為避免類似事故的再次發生，以減少人員傷亡和資源經濟損失，礦山安全監管部門聯合相關部門決定建立采空區穩定性預警機制，在對礦區礦山現有采空區進行穩定性評價后，再針對穩定性不佳的采空區采取措施進行處理。經統計分析，采用分層抽樣的方法抽取部分礦山采空區作為樣本采空區，樣本采空區的基本情況如表1所示。

表1 樣本采空區基本參數

注：地應力及圍巖質量評分數均為該采空區的平均值或綜合評價值。

2.2 采空區穩定性分級標準

經統計，該市礦山深部礦床采空區暴露面積一般為50~170 m2，采空區所受的地應力(包括自重應力及構造應力)范圍為40~100 MPa，根據專家評分法，對采空區的臨時支護方式評分范圍為30~90分，該礦山的圍巖質量評價采用南非RMR法進行評價，巖體質量評分范圍為20~80分。對礦區礦山采空區的穩定性按照穩定、一般穩定及不穩定進行3級分類。對采空區穩定性而言，采空區暴露面積越小越穩定，地應力越小越穩定，支護方式及圍巖質量評分越高越穩定，據此得分級標準如表2所示。

表2 采空區穩定性分級

2.3 聯系度計算

將樣本采空區各指標因素歸集為采空區暴露面積集合1、地應力集合2、支護方式評分集合3和圍巖質量評分集合4。將各指標對應的穩定性等級為Ⅰ級(穩定級別)的評價標準歸集為集合1-。構建集對(A,1)(=1，2，3，4)。根據式(4)和(6)的模糊隸屬關系計算出集對(A,1)的3元聯系度，各指標因素的模糊隸屬關系聯系度如圖3所示。

(a) 采空區暴露面積；(b) 地應力；(c) 支護方式評分；(d) 圍巖質量評分

各采空區指標因素對應于等級Ⅰ(穩定級別)的聯系度計算結果如表3所示。

表3 各集合對H(Al,B1)的聯系度

2.4 指標權重計算

以樣本數據為基礎，利用變異系數法計算各指標權重，根據表1 中的樣本數據，得采空區暴露面積的標準差1=38.18，平均值=96.92；地應力的標準差2=15.94，平均值=67.46；支護方式評分的標準差3=17.43，平均值=62.10；圍巖質量評分的標準差4=13.62，平均值=51.93。根據式(8)，得采空區暴露面積的變異系數1=0.393 9，地應力的變異系數2=0.236 3，支護方式評分的變異系數3=0.280 6，圍巖質量評分的變異系數4=0.262 2。

根據式(9)，對各指標變異系數進行歸一化處理，得各指標因素權重為：采空區暴露面積權重1=0.34，地應力權重2=0.20，支護方式評分權重3=0.24，圍巖質量評分權重4=0.22。

2.5 綜合聯系度計算

根據式(10)，以表3中的數據及各指標因素權重為基礎，計算得各樣本采空區對于所有指標Ⅰ級(穩定級別)評價等級標準的3元聯系度(,)如表4所示。

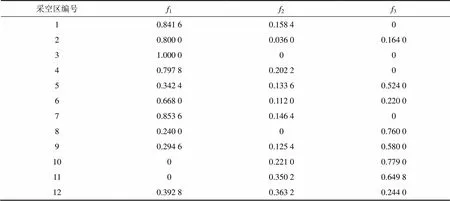
表4 樣本采空區集對H(A,B)的聯系度

2.6 置信度準則判定

由于采空區穩定性分析關系礦山正常生產與人員設備安全，因此，采用的置信度應該偏大，取置信度=0.6。

據式(12)，得各采空區的置信度準則判定結果如表5所示。

表5 采空區穩定性置信度準則判定結果

由表5可見：以12號采空區為例，Ⅰ級(穩定)的聯系度(0.392 8)與Ⅱ級(一般穩定)的聯系度(0.363 2)相差并不大，且各級別中最大聯系度小于0.500 0，若按照最大隸屬度原則判定為穩定，則屬于非穩定級別的聯系度值遠大于穩定級別，因此是不科學的，容易造成事故。而按照置信度原則判定法判定為Ⅱ級(一般穩定)，相對于判定為Ⅰ級(穩定)采取了更為嚴格的采空區維穩措施，有效保證了采空區的穩定，避免了潛在安全事故的發生。

2.7 采空區維穩對策擬定

根據置信度準則對樣本采空區穩定性的判定，對采空區穩定性評價為Ⅲ級即不穩定的5號、8號、9號、10號和11號采空區，應采取嚴格的應對支護措施，除留不規則礦柱外，還采用加密錨桿及加厚噴漿的方式以維持采場的穩定性；對采空區穩定性評價為Ⅱ級即一般穩定的12號采空區，留4 m×4 m的不規則礦柱以維持采場的穩定性；對采空區穩定性評價為Ⅰ級即穩定的1號、2號、3號、4號、6號和7號采空區，可以考慮不予處理或用臨時支護手段進行處理。經統計，采用上述穩維措施后，采空區穩定性破壞率降低了50%左右，而采空區維穩成本也降低了約30%。

3 結論

1) 以模糊集對分析理論建立模型對采空區穩定性進行了評價，通過對樣本采空區的穩定性的分析評價與相應的對策措施證明，模糊集對分析可實現對采空區穩定性的預判，從而對采空區的維穩進行指導，其過程科學，結果可靠，是依靠數學理論對采空區穩定性分析評價的一種新方法。

2) 利用變異系數法對各指標權重進行了計算，相對于傳統的層次分析法等權重指標計算方法，變異系數法完全以樣本數據為依據，不以人的主觀偏好為轉移，相對科學，計算的指標權重更可信。

3) 采用置信度準則對采空區穩定性等級進行判定，有效避免了采用最大隸屬度原則時由于可能存在的多種屬性的隸屬度差別不大，或最大隸屬度小于0.500 0，而造成不合理判定的問題。同時，提出相應的維穩對策，使采空區穩定性破壞率降低約50%，成本降低約30%。

參考文獻：

[1] HU Yuxi, LI Xibing. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 425?431.

[2] 舒服華. 基于改進灰色關聯分析的鑄鐵綜合性能評價[J]. 鑄造, 2007, 56(2): 162?164. SHU Fuhua. Evaluation of iron casting overall performance based on improved grey relational grade[J]. Foundry, 2007, 56(2): 162?164.

[3] 楊松林, 王夢恕, 周曉敏. 灰色關聯分析在豎井凍結壁“窗口”事故處理中的應用[J]. 煤炭學報, 2005, 30(4): 467?471. YANG Songlin, WANG Mengshu, ZHOU Xiaomin. Application of grey correlative analysis for disposal of the freezing wall “window” accident[J]. Journal of China Coal Society, 2005, 30(4): 467?471.

[4] SU Meirong, YANG Zhifeng, CHEN Bin. Set pair analysis for urban ecosystem health assessment[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(4): 1773?1780.

[5] 李連祥, 馮玉國. 基于集對分析聯系數的區間型基坑支護方案綜合評價方法及其應用[J]. 數學的實踐與認識, 2015, 45(1): 132?138.LI Lianxiang, FENG Yuguo. A comprehensive evaluation of method of interval supporting schemes for foundation pit based on connection number of set pair analysis and its application[J]. Mathematics in Practice and Theory, 2015, 45(1): 132?138.

[6] 王文圣, 李躍清, 金菊良, 等. 水文水資源集對分析[M]. 北京: 科學出版社, 2010: 85?99. WANG Wensheng, LI Yueqing, JIN Juliang, et al. Set pair analysis for hydrology and water resources systems[M]. Beijing: Science Press, 2010: 85?99.

[7] 張志鎮, 高峰, 許愛斌, 等. 沖擊地壓危險性的集對分析評價模型[J]. 中國礦業大學學報, 2011, 40(3): 379?384. ZHANG Zhizhen, GAO Feng, XU Aibin, et al. Model for estimating rock burst risk in a coal mine based on set pair analysis[J]. Journal of China University of Mining & Technology, 2011, 40(3): 379?384.

[8] 劉亞群, 李海波, 裴啟濤, 等.基于灰色關聯分析的遺傳神經網絡在水下爆破中質點峰值振動速度預測研究[J].巖土工程, 2013, 34(S1): 259?264. LIU Yaqun, LI Haibo, PEI Qitao, et al. Prediction of peak particle velocity induced by underwater blasting based on the combination of grey relational analysis and genetic neural network[J]. Rock and Soil Mechanics, 2013, 34(S1): 259?264.

[9] HU Junhua, YANG Liu. Dynamic stochastic multi-criteria decision making method based on cumulative prospect theory and set pair analysis[J]. Systems Engineering Procedia, 2011, 1(1): 432?439.

[10] 劉棟, 史秀志, 張舒, 等.基于集對分析的非煤礦山緊急避險能力評價[J]. 安全與環境學報, 2014, 4(2): 85?89. LIU Dong, SHI Xiuzhi, ZHANG Shu, et al. An improved evaluation model for non-coal mine emergency rescue capability based on the set pair analysis theory[J]. Journal of Safety and Environment, 2014, 4(2): 85?89.

[11] XIE Naiming, LIU Sifeng. Research on evaluations of several grey relational models adapt to grey relational axioms[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 304?309.

[12] 菅利榮. 面向不確定性決策的雜合粗糙集方法及其應用[M]. 北京: 科學出版社, 2008: 82?94. JIAN Lirong. Facing the heterozygous uncertainty decision- making rough set method and its application[M]. Beijing: Science Press, 2008: 82?94.

[13] 謝正文, 吳超, 李孜軍, 等. 基于信息熵和集對分析理論的硫化礦石自燃傾向性判定[J]. 中南大學學報(自然科學版), 2012, 43(5): 1858?1863. XIE Zhengwen, WU Chao, LI Zijun, et al. Evaluation on spontaneous combustion tendency of sulfide ores based on entropy and set pair analysis theory[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1858?1863.

[14] 張文修, 仇國芳. 基于粗糙集的不確定決策[M]. 北京: 清華大學出版社, 2005: 13?27. ZHANG Wenxiu, QIU Guofang. Based on rough sets of uncertain decision[M]. Beijing: Tsinghua University Press, 2005: 13?27.

[15] 劉同明. 數據挖掘技術及其應用[M]. 北京: 國防工業出版社, 2001: 156?188. LIU Tongming. Data mining technology and its application[M]. Beijing: National Defense Industry Press, 2001: 156?188.

[16] 王國胤. Rough集理論與知識獲取[M]. 西安: 西安交通大學出版社, 2001: 117?138. WANG Guoyin. Rough sets theory and knowledge acquisition[M]. Xi’an: Xi’an Jiaotong University Press, 2001: 117?138.

Application of fuzzy set pair in stability evaluation of mining goaf

LIU Lang1, 2, CHEN Zhongqiang3

(1. Energy School, Xi’an University of Science and Technology, Xi’an 710054, China;2. Key Laboratory of Western Mines and Hazards Prevention, Ministry of Education of China, Xi’an 710054, China;3. Beijing General Research Institute of Mining and Metallurgy, Beijing 100070, China)

Considering that the underground mine goaf instability can easily cause high casualties and property damage, and that the stability of mine goaf is hard to prejudge, fuzzy set pair analysis was carried out on goaf stability evaluation. Four influential indicators of goaf stability such as goaf area, stress, support method and surrounding rock quality were considered. Stability degree was divided into 3 grades on 12 sample goafs, and fuzzy membership relation was used to calculate connection degree of goaf factors corresponding to each index. Combined with the weight of each indicator, comprehensive connection degree of each goaf was obtained, and the stability of each goaf was evaluated based on confidence criterion. The results show that the proposed method can be used for mining goafs stability evaluation, and the corresponding strategies used for golfs supporting can reduce failure rate by 50%, while the cost reduce by 30%.

goaf; stability; fuzzy; set pair analysis

10.11817/j.issn.1672-7207.2015.07.038

TD05

A

1672?7207(2015)07?2665?08

2014?11?15；

2015?01?20

陜西省自然科學基金資助項目(2015JQ5187) (Project(2015JQ5187) supported by the Natural Science Foundation of Shanxi Province)

劉浪，博士，從事采礦與安全系統工程方面的研究；E-mail: csuliulang@163.com

(編輯 劉錦偉)