淺析鐵板輸送機構設計原理

張哲暢　+張俐

摘要:針對鐵板輸送機的規定長度并執行剪切工藝的要求，對整個輸送機的結構特點做了分析，同時對整體進行了結構方案的對比分析，針對給出方案重點設計了四連桿部位，實現了鐵板輸送機的整體功能，證明該方案的可行性。

關鍵詞：鐵板輸送機；結構設計；四連桿設計

1簡介

鐵板輸送機又叫“開卷機”。屬于通用機械。鐵板輸送機是集項目設計與制作各類光機電一體化物流輸送設備，它包括夾持和輸送鐵板，并在停歇時保搶救無效鐵板的待剪位置；能夠實現間歇送進，并能使鐵板停歇時，運送鐵板的構件的速度的加速度曲線仍然連續，使整個機構的運轉比較平穩。

其結構一般具有以下特點：

（1）它每次輸送鐵板長度一般為為1900mm、2000mm或2200mm[1]。

（2）剪斷工藝所需時間約為鐵板輸送周期的1/15．要求鐵板停歇時間不超過剪斷工藝時間的1.5倍，以保證能有較高的生產率[1]。

（3）輸送機[2]構運轉應平穩，振動和沖擊應盡量小(即要求輸送機構從動件的加速度曲線連續無突變)。

（4）自動化按鈕控制,安全,便當。

（5）安全標識和安全標簽,確保使用安全。

（6）可以配備輸送帶加料。

鐵板輸送機的工藝流程較為固定：鐵板夾持→鐵板輸送→剪切鐵板→工件成形，其中，本次設計主要為鐵板的輸送。

為了實現鐵板的輸送，主要需要針對運動機構進行分析。 由于鐵板輸送機工作和停頓的工作特點，可以考慮用間歇傳動機構，本文對比分析了兩種間歇傳動機構（不完全齒輪機構和齒輪連桿間歇運動機構），同時對運動機構做了詳細設計，得出符合要求的四連桿設計尺寸。

2間歇傳動機構的選擇

由于鐵板輸送機工作和停頓的工作特點，可以考慮用間歇傳動機構[3]。間歇傳動機構的方式有很多，主要有通過不完全齒輪機構和齒輪—連桿機構兩種方式。

2.1不完全齒輪機構

常用的間歇傳動機構選擇采用的是不完全齒輪機構的形式，該形式主要具有結構簡便的優點。不完全齒輪是由一般的全齒輪機構演變而來，與一般的的全齒輪相比，最大的區別在于齒輪的整個圓周上沒有布滿輪齒[4]。

要求“剪斷工藝所需時間約為鐵板輸送周期的十五分之一”，反映到主動齒輪上要求有齒部分與無齒部分之比為14:1，根據實際生產過程中所要求，每次進給2200mm,所以我們假設輪轂直徑D=900mm。

解得θ=280°，即當主動齒輪旋轉一個周期T的過程中，從動齒輪旋轉280°。主動齒輪有齒部分為336°，無齒部分角度為24°，這樣即可滿足1/15的比列,利用solidworks的toolbox中的齒輪插件我們先選定從動齒輪z2=82,m2=5mm,如圖1，給齒輪d=385mm,這個尺寸可以滿足傳送強度要求，并且接近整數。

2.2齒輪—連桿間歇運動機構

齒輪—連桿間歇運動機構相對前者有運轉平穩，振動沖擊都比較小的優點，能更好的控制每次運動的時間[5]。

4極電機額定轉速為1440r/min，我們將電動機與渦輪先用傳送帶連接，減小轉速，再通過渦輪蝸桿連接，進一步減小轉速。運動方案簡圖如圖２所示。

2.3優缺點對比

兩種方式各有優缺點，兩種方案對比如表1。

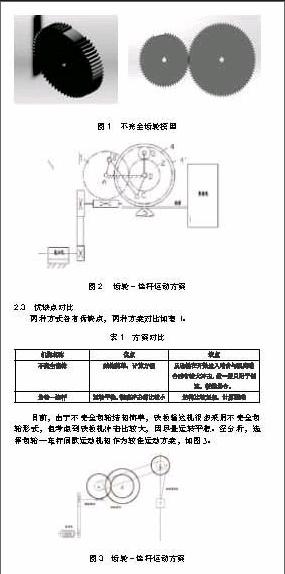
目前，由于不完全齒輪結構簡單，鐵板輸送機很多采用不完全齒輪形式，但考慮到鐵板機沖擊比較大，因盡量運轉平穩。經分析，選擇齒輪—連桿間歇運動機構作為較佳運動方案，如圖3。

3四連桿尺寸確定

結合前面方案的選定，需要對四連桿的尺寸做設計。由上面的分析可知，曲柄搖桿機構應該滿足三個條件[6]：

（1）曲柄AB轉過30度（約為1/15，計算簡單）時每一瞬間主動件跟從動件要滿足關系：

（2）桿長應滿足曲柄存在條件，保證主動件能作整周回轉；

（3）傳動角。（圖４）用反轉法[7]確定各桿長度，先假設AB=100mm,初始角度為60°，根據上面的公式確定：

當時，；。

可得：BC=687.49mm,CD=321.06mm。

因為BC+CD>AB＋AD，所以滿足桿長條件，最小壓力角：

滿足最小傳動比關系。

所以各桿長度分別為：

AB=100mm,BC=687.49mm,CD=321.08mm,AD=600mm。

根據以上計算，四連桿的尺寸是可以確定的，同時，結合四連桿的設計尺寸和傳動要求能夠確定周轉輪系的齒輪參數。經過尺寸設計，模擬裝配模型如圖5。

4結論

本文重點分析鐵板輸送機的傳動機構的方案選擇和針對特定情況下工況的四連桿的設計，從設計結果來看，該方案的設計計算并不是特別復雜，具有很強的可行性，能夠通過計算得出傳動機構的尺寸，同時能夠穩定的實現鐵板輸送機傳動的特點。

參考文獻：

[1]曾小惠,王玉丹,路桂英.機械原理課程設計指導書[S].中國地質大學機電學院,2012(05).

[2]成大先.機械設計手冊[S].北京:化學工業出版社,2010.

[3]關玉明,張文雅.間歇機構—不完全齒輪的設計及應用[J].機械工程與自動化,2009,07(07).

[4]王猛.不完全齒輪自動換向機構傳動性能的研究[D].濟南:濟南大學,2010.

[5]陳璟.齒輪連桿機構的分析與綜合[D].福建:福州大學,2004.

[6]富廣祥,陳書慶,魏燕生.四連桿機構運動分析簡便方法[J].機械工程師,1988(03).

[7]孫恒,陳作模,葛文杰.機械原理[M].北京:高等教育出版社,2006(05).endprint