基于小生境遺傳算法的兩棲車輛車輪收放裝置的優化

包振明，王琪，徐一新，唐蘇

（1.江蘇科技大學能動學院，江蘇 鎮江 212003；2.江蘇科技大學機械學院，江蘇 鎮江 212003）

基于小生境遺傳算法的兩棲車輛車輪收放裝置的優化

包振明1，王琪2，徐一新2，唐蘇2

（1.江蘇科技大學能動學院，江蘇 鎮江 212003；2.江蘇科技大學機械學院，江蘇 鎮江 212003）

文章根據水陸兩棲車輛的車輪收放裝置的特點, 建立改進型雙橫臂獨立懸架的靜力學和運動學模型，運用小生境遺傳算法，在MATLAB中開發了多目標的優化程序，通過高次迭代排除干涉項，求取到了全局最優解。并進一步在 ADAMS中建立懸架的運動學模型，驗證其優化設計的可行性，仿真分析表明，優化后的結果達到懸架設計的性能指標，是一種水陸兩棲車輛車輪收放裝置中懸架系統的有效設計新方法。

兩棲車輛；雙橫臂獨立懸架；車輪收放裝置；小生境遺傳算法

10.16638/j.cnki.1671-7988.2015.09.015

CLC NO.: U463 Document Code: A Article ID: 1671-7988(2015)09-41-05

引言

兩棲車輛的發展中，水阻力一直是影響車輛水中行駛速度的主要因素之一。而車輪在水中形成的附著阻力占總的水阻力比率相對較大。因此，如何在水中將車輪收起以實現減阻增速是兩棲車輛研究的關鍵之一[1-2]。現有的車輪收放裝置有兩種，一種為垂直升降車輪，另一種是翻轉式收放車輪[3-4]。這兩種都是通過對懸架導向機構進行改進，從而達到收放車輪的目的。其中翻轉式車輪收放裝置結構操作較為穩定，且對垂直方向的空間要求相對較低，更能符合懸架的空間布置。

兩棲車輛中車輪收放對懸架的結構產生了影響，而懸架的運動特性直接與車輛在陸地行駛過程中的操縱穩定性、行駛平順性和輪胎使用壽命等因素相關。故建立、求解懸架的運動學模型，確定懸架的空間幾何參數、變化規律對整車性能有重要意義。由于雙橫臂獨立懸架具有輪距變化小、車輪相對車身跳動時車輪定位參數變化小、結構緊湊等優點，在輪式車輛上得到廣泛應用，同時也適應于兩棲車輛。因此，針對雙橫臂獨立懸架一些學者運用多體動力學、矢量法等不同的數學方法求解運動特性，并進行優化設計[5-9]。還有學者結合采用權重值系數變換法將多目標轉化為單目標的遺傳算法，求解不同側重問題的最優解，以改善懸架某方面的運動特性[10-12]。還有一些學者基于 ADAMS，通過建立虛擬樣機模型，通過隨機的改變模型參數，以提高導向機構的運動特性[13-15]。

本文針對改進的兩棲車雙橫臂獨立懸架，結合有限轉動張量，建立了懸架的數學模型，通過小生境遺傳算法（NGA），設立多目標的優化算法，以求得高次迭代后的最優解。并于ADAMS中建立車輛模型，用以驗證所求解收放裝置的合理性。

1、數學模型的建立

1.1簡化車輪收放裝置的空間幾何模型

雙橫臂獨立懸架的結構示意如圖1所示。為了實現車輪的主動收放，設計一種主動控制的油氣彈簧懸架，并對雙橫臂獨立懸架進行改進，將傳統A字橫臂拆開，得到收放裝置的機構模型，如圖2所示。圖2中和A′′ H為下擺臂，繞軸線GH轉動，取GH中點為D；EB′和B′′ F為上擺臂，繞軸線EF轉動，取EF中點為C。A、B點分別為上下球節點，即AB表示主銷軸線；W點為車輪中心，車輪軸線WN交AB于N點；K點為輪胎接地點，且WN⊥WK；M、P點分別為橫拉桿內外球節點，轉向節臂MJ交AB于J點，且MN⊥AB。為了分析導向機構的運動，動坐標系的原點O選在車輪中心和車輛中心平面的交點上，過O點的平行于車輛前進方向（平行于汽車的縱向軸線）為X軸的正向，Z軸為垂直向上。Y軸通過O點并與X軸與Z軸正交，指向車輪。

1.2收放裝置的靜力學模型

由于 B′ B′和A′ A′相對整體導向機構的長度較小，所以在設計計算中可以忽略。故收放裝置在橫向和縱向平面投影，如圖3和4所示。并由懸架的空間布置，知K點坐標（0,T/2,-r）和車輪外傾角α，得W點坐標：

B點坐標為

C點坐標為：

同理可求得D點坐標。

機構于水平面的投影，如圖5。根據已求得的C、D的坐標，EF在縱向平面上的投影與X軸的夾角，EF在縱向平面上的投影與X軸的夾角 θ3，可以求得E、F點的坐標。E點的坐標為：

同理可得，F、G、H點的坐標。則可知機構的瞬時中心IC的坐標，IC的坐標為：

側傾中心高度可得：

及車輪側偏量

1.3收放裝置的運動學模型

設車輪激振過程中，下橫臂和上橫臂分別繞各自的方向矢量轉動σ和ω角，則根據系統動力學中的有限轉動張量原理，求取轉角σ和ω之間的關系為：

A′為A點繞方向軸線 EF旋轉某一角度σ后得到的。根據空間運動學的空間坐標變換原理，A′的坐標為：

而

由于E、F、G、H、P點的坐標沒有變化，根據空間幾何解析，有M點到A、B、P的距離不變，則

瞬時主銷內傾角

瞬時主銷后傾角

車輪前束量

2、小生境遺傳算法（NGA）

2.1小生境遺傳算法原理

小生境思想源于一種奇特的生物現象：在一定的生存空間下，相似的生物必須通過相互競爭以取得各自有限的生存資源，而相異的個體由于生活習性的較大差異很少競爭；從而物種生活在各自的特定的環境下。此種生存環境，被稱為小生境（Niche）［16］。

小生境的基本思想是：在多元多峰值函數的優化過程中，首先將解空間劃分為多個小生境域，再讓相似個體在特定的小生境域中不斷進化，以達到該生境域內的峰值，最后在全生境的峰值間尋求最優解。小生境遺傳算法可以有效提高傳統遺傳算法的優化效率；并避免陷入局部最優解。

2.2設計變量

根據上述表達式及懸架導向機構的空間情況，確定設計變量為：

1）下擺臂球銷轉動中心點A（xa,ya,za）；

2）下擺臂長度 lAD；

3）上下擺臂長的比值 c1；

4）主銷與下擺臂的比值 c2；

5）靜平衡狀態時，上下擺臂于橫向平面中的傾角θ1、θ2；

6）上下擺臂轉軸的斜置角θ3、θ4；

7）上下擺臂與X軸的夾角θ5、θ6；

8）轉向節臂球外鉸點M（xm,ym,zm）；

10）主銷內傾角β、主銷后傾角δ、車輪外傾角α。

因此設計變量為21個，即：

2.3 目標函數

根據懸架的設計要求，可確定車輪收放裝置在優化設計中的目標函數如下。

1）前輪各定位參數特性。表達式為：

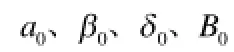
2）為減小輪胎的磨損，盡量減小輪胎側滑量的表達式為：

3）為減小汽車在制動和加速行駛時因慣性力產生的載荷轉移而導致的制動時的“點頭”和驅動加速時的“抬頭”現象，懸架系統應具有足夠的抗點頭效果。抗點頭率的表達式為：

其中h為汽車質心高度；L為軸距；r為制動力分配系數；e為點IC′的高點；d為點IC′在X軸上的絕對值。當車輛整體參數確定時，h、L、r都為固定值，則抗點頭率的表達式為：

根據設計要求，此懸架具有收放功能，故導向機構運動空間所占體積應該盡量最小，以減少運動干涉及輪艙體積，則體積的表達式為：

2.4約束條件

本文根據車輪收放導向機構的設計要求，確定如下約束條件：

2）下擺臂長度0≤lAD≤maxlAD；

3）上下擺臂長的比值0.6≤c1≤1；

4）主銷與下擺臂長的比值0.6≤c2≤1；

2.5算法的實施

本文采用并列選擇法來求解多目標優化問題的最優解，即先將群體中的全部個體按子目標函數的數目均等地劃分四份，對每個子群體分配一個子目標函數，各子目標函數在各自的群體中進行運算，從而選擇出一些適應度高的個體，并將這些個體組成一個新的子群體，然后再將所有新群體組成一個完整的群體，在新的群體中進行交叉和變異運算，如此不斷地“分割—并列選擇—合并”，以求得最優解。

3、車輪收放裝置的仿真模型

根據所得解和車體結構， 利用ADAMS軟件， 建立如圖6所示的收放裝置的運動學仿真模型， 并確定各點參數如表 1所示。

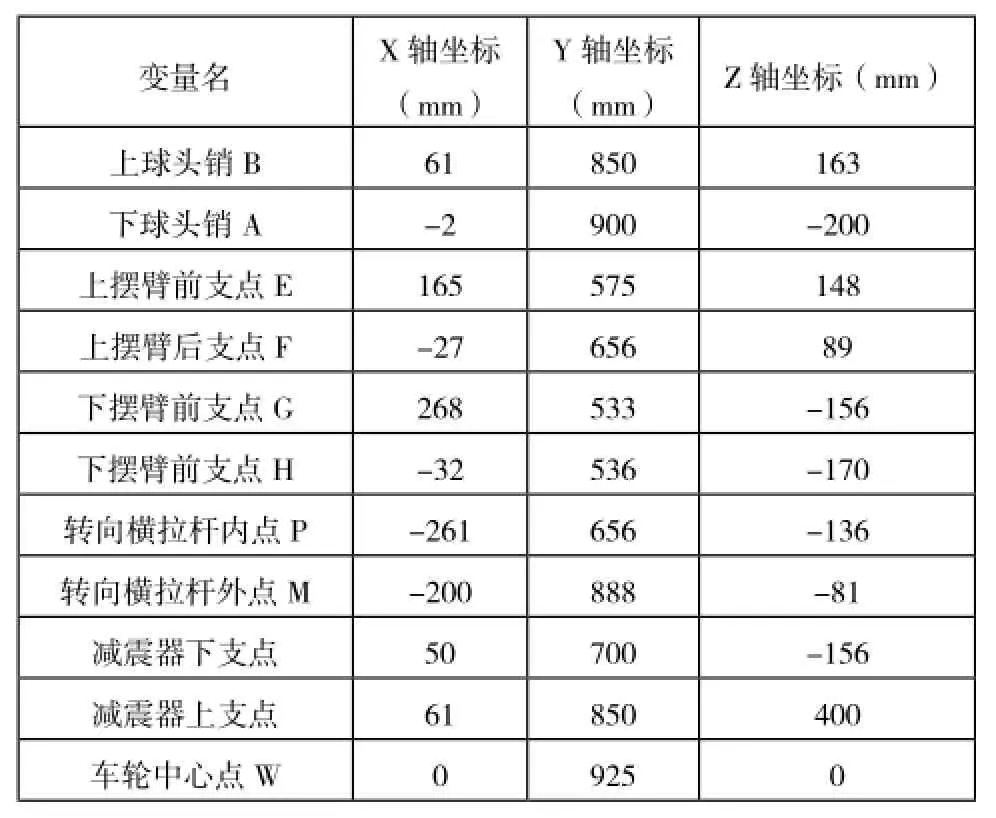
表1 前懸架各定位點的坐標

由于ADMAS模型中沒有油氣彈簧模型，故使用螺旋彈簧，來代替，而將彈簧特性設為油氣彈簧特性。其一端連接于下橫臂上，另一端連接車身。由于使用了特殊的油氣彈簧結構，可以將車輪位置根據行駛需要來主動調節，實現輪胎的收放。其前減震器的安裝角為15.1o。

4、仿真分析

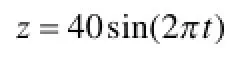
、變異概率Pm =0.01時，懸架性能較好。因ADAMS軟件內部不存在程序設計及優化輔助分析的設置，故本文采用MATLAB語言編寫了小生境遺傳算法優化程序, 建立數學模型，通過約30代迭代，得最優的10組解，并分析各解的機構模型，排除運動干涉解，從而得到最優解。模型的仿真分析結果如圖7-10所示。

從優化后的結果可以看出，主銷內傾角實際設計時，大致范圍為：7°～13°，希望取較小的數值，本文所得角度為7.5°。主銷后傾角一般認為0°～ 10°是合理的范圍，本文取 9.7°。當車輪跳動過程中，外傾角變化為-2°～-0.5° /50mm。而且前輪的前束角變化范圍為0～1°/50mm，變化范圍合理且幅度較小，滿足設計要求。故優化后的各參數值的變化范圍較為理想，且在滿足兩棲車收放功能的前提下，機構有良好的運動特性。

5、結論

本文利用小生境遺傳算法和并列選擇法，結合兩者優點對某水陸兩棲車的車輪收放裝置，即改進型雙橫臂獨立懸架進行了運動學多目標優化設計計算，通過高次迭代后，排除干涉解，取得了全局最優解，并結合多體系統動力學，利用ADAMS軟件，通過仿真，驗證兩棲車收放裝置的運動特性。結果表明，利用小生境遺傳算法可以進行復雜空間系統的結構參數優化設計，并獲得懸架系統的有效設計方法。

[1] 徐一新,李書偉王琪等.基于組合建模法的兩棲車輛車體優化分析[J].計算機仿真，2013（03）：173-176，183.

[2] 劇冬梅,李軍.輪式兩棲車輛關鍵技術研究[J].汽車運用，2013（05）：5-6.

[3] Gary M Gere,Russell L Holder,Louis J Musetti,Ray Ramsey.Amphi -bious vehicle:USA, 444829 [P].1995-05-18.

[4] Alan Timothy Gibbs.Amphibious vehicle:GB,134953.11[P].2005 (05)：23.

[5] 丁飛,韓旭,劉桂萍等.懸架導向機構硬點靈敏度分析及多目標優化設計[J].汽車工程,2010，32(2):137-142.

[6] 施睿,趙春霞.雙橫臂獨立懸架運動學分析與優化設計[J].車輛與動力技術,2014（03）:35-41.

[7] 楊波,左曙光,覃霍,韓樂.雙橫臂獨立懸架導向機構硬點匹配設計[J].機械設計與制造,2010（10）：65-67.

[8] 陳加國,宗亞平.雙橫臂獨立懸架運動特性仿真與分析[J].汽車零部件,2013（ 8）：86-88.

[9] 潘國昌,黃虎,劉新田,劉長虹.雙橫臂獨立懸架運動學仿真分析[J].機械設計與制造,2009（11）：200-202.

[10] 陳黎卿，陳無畏，何欽章.雙橫臂扭桿獨立懸架多目標遺傳優化設計[J].中國機械工程學報，2007，18(17)：2022-2025.

[11] 陳羽,劉江南,韓旭等.雙橫臂式前獨立懸架的改進遺傳算法優化[J].中國機械工程學報,2007，18(22)：2756-2759.

[12] JASZKIEWICZ A. Genetic local search for multi-objective combin -atorial optimization [J]. European Journal of Operational Research, 2002(01):50-71.

[13] 舒勇.ADAMS在汽車雙橫臂獨立懸架運動特性分析中的應用[J].汽車實用技術,2013（05）:16-19.

[14] 張亮亮,裴永生,吳丹丹.基于 ADAMS的雙橫臂獨立懸架的仿真分析及優化設計[J].現代機械,2010(04):27-29.

[15] Cavicchio D J.Reproductive Adaptive Search Using Simulated Evolution [D].Ann Arbor,USA:University of Michigan,1970.

[16] 武興亮,丁根宏.改進小生境遺傳算法求解多峰函數優化問題[J].信息技術,2013（1）：73-76.

The Optimization Design of the Wheel’s Retracted and Amphibious Vehicle Using Niche Genetic Algorithm

Bao Zhenming1, Wang Qi2, Xu Yixin2, Tang Su2
( 1. Dynamic, Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003;
2. Mechanical Engineering, Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003 )

The statics model and dynamics model for the improved-double-wishbone independent suspension guide mechanism and deployed for the amphibious vehicle are established, according to the characteristics of device’s retracted. Using the niche genetic algorithm, a multi-objective optimization program in MATLAB to verify the feasibility of the solution after the high iteration. Tthe global optimal solution was obtained. A kinematics model in ADAMS is made. The results achieved the design performance index of the suspension. An effective method to design the suspension system obtained.

Amphibious vehicle; Double-wishbone independent suspension; Retracted and deployed Device; NGA

U463

A

1671-7988（2015）09-41-05

包振明，就職于江蘇科技大學，研究方向為輪機工程。

國家自然科學基金項目（61105071）和江蘇省產學研前瞻性聯合研究項目（BY2012179）的資助。