證據理論在Bayes可靠性評估中的應用

馬麗娜（西安財經學院 行知學院信息系，陜西 西安 710038）

證據理論在Bayes可靠性評估中的應用

馬麗娜
（西安財經學院 行知學院信息系，陜西 西安 710038）

提出了一種基于D-S證據理論的 Bayes可靠性評估方案，很好地表達和利用了Bayes方法中的“不確定的”先驗信息。在無替換定數截尾試驗樣本下，研究了指數壽命型產品的可靠性指標的估計問題，提出了可靠性評估的兩種方法：通過融合可靠性指標的后驗分布進行綜合評估和通過融合可靠性指標的后驗置信區間進行綜合評估。數值實例表明，利用所提出的方法得到的評估結果是“謹慎的”和合理的。

D-S證據理論；Bayes方法；可靠性；LC準則；Pignistic概率

0　引言

在大型復雜產品的可靠性評估過程中，由于時間、經費、保密等因素的限制，客觀可靠性信息往往難以獲取或者獲取的成本較高，每次試驗的樣本量較少，因此利用經典統計方法很難對復雜產品可靠性參數做出精確的估計。而Bayes統計方法能夠把工程技術人員對產品的了解、經驗、類似產品的可靠性信息綜合起來，對小樣本也有比較好的統計推斷效果。因此，Bayes方法在復雜產品的可靠性評估中得到了廣泛的應用。

在Bayes統計中，驗前分布的獲取和表示是一個關鍵的問題。在產品的可靠性評估中，特別是對新型復雜產品，往往會遇到“無信息”或先驗信息難以表示的情況。此時，通常會采用Jeffreys原則或“共軛分布法”來確定先驗分布。利用這些形式的先驗信息再結合樣本和總體信息進行統計推斷具有一定的主觀性和不確定性。D-S證據理論作為一種重要的不確定推理的方法，可以很好地表達和處理這種不確定信息，從而為復雜產品的可靠性評估提供了一種新的途徑。

1　相關理論分析

1.1證據理論

［1］詳細介紹了證據理論的基礎知識，現簡述如下。

定義1 設Θ是X的識別框架，則函數m［0，1］稱為 2Θ上的基本信度分配（BBA）函數，如果滿足：

其中，m （A）是對命題x∈A的精確信任程度的一種度量，表示了對A的直接支持，通常稱為A的mass值。對空集Φ分配的基本信度m（Φ）代表了識別框架的不一致性和不完整性。

D-S證據理論提供了一個有用的合成公式，使人們能融合多個證據源提供的證據。

定義2設m1和m2是同一識別框Θ上的兩個BBA，焦元分別為 A1，…，Ak和B1，…，Br，則：

其中，N=ΣAi∩Bj=Φm1（Ai）m2（Bj）＜1。式（2）給出的組合規則稱為Dempster證據組合規則。

1.2Pignistic概率

在D-S證據理論中，可用Pignistic概率轉換公式將BBA轉換成一種概率度量。最常用的轉換方法是平均分配法（Smets法），認為每一個元素出現的概率一樣，因此把多元素命題的BBA值平均分配給所包含的元素［2］。

其中，|A|為集合A的勢；m（Φ）是對空集的BBA，代表了證據的不一致性。

1.3最小特異性原則

如果已知目標識別框架上的Pignistic概率，如何從滿足此不確定性描述的證據中選擇最合理的一條呢？有學者提出，利用最小特異性（Least Committed）原則選出“最謹慎”的一條證據［3］。在這個準則下的最優證據攜帶的確定性信息最少。

RISTIC B和SMETS P等人［4］研究了連續空間上的證據理論和LC原則，并指出如果Pignistic概率是單峰的，那么在LC原則下滿足此Pignistic概率的最優BBA由式（4）決定：

其中，Bet f（s）=Bet f（Φ（s））。

2　指數壽命模型可靠性分析

在Bayes可靠性評估中，如果遇到對參數先驗信息不足的情況，常采用 Jeffreys原則或“共軛分布法”來確定先驗分布。利用這些形式的先驗信息再結合樣本和總體信息進行統計推斷具有一定的主觀性和不確定性。根據證據理論的思想，此時可把得到的參數后驗分布當作Pignistic概率，再由證據理論處理這些不確定信息。

指數分布是最簡單的失效分布，但是在可靠性試驗及其統計分析中占有相當重要的地位。現在考慮指數壽命型產品的可靠度的評估。

方案1通過融合可靠度的后驗分布進行綜合評估

根據Bayes公式，可得Jeffreys原則和“共軛分布”思想下，可靠度的后驗密度函數分別為：

把它們當作Pignistic概率密度，由式（4）可得其對應的LC準則下最優BBA分別為：

由證據組合規則融合上面兩個BBA可得一個綜合的BBA：

按照平均分配法的思想進行Pignistic概率轉換：

其中，ρ是一個與x無關的常數，使得 Bet f（y）成為一種概率度量。Bet f（y）是對可靠度進行評估的依據。

下面看一個具體實例。設某電子設備的壽命服從指數分布。任取15臺進行無替換定數截尾壽命試驗，事先規定失效數 r=7，試驗結果為（單位：h）：t1=500，t2= 1 350，t3=2 130，t4=2 500，t5=3 120，t6=3 500，t7=3 800。現在要對該電子設備的t0=500 h時的可靠度進行評估。利用上述評估方案，可得在t0=500 h時該電子設備的可靠度的Pignistic概率密度函數如圖1所示。將所得結果與在 Jeffreys準則和“共軛分布”思想下得到的 t0=500 h時的可靠度的概率密度函數進行對比，如圖2所示。

圖1　Pignistic概率密度函數

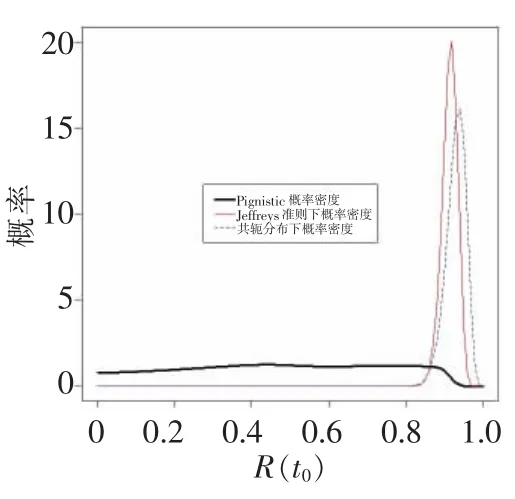
圖2　t0=500 h時指數分布可靠度的三種概率密度函數

方案2通過融合可靠度的后驗置信區間進行綜合評估

從上面可以看出，直接從后驗分布出發構建 Pignistic概率計算上較為復雜，本文提出一種從可靠度的置信區間出發進行綜合評估的簡單方法。此時，目標識別框為［0，1］上的區間集合。

設已經得到了可靠度的n個不同置信水平的置信區間 A1，…，An，置信度分別為 1-α1，…，1-αn，把其當作Θ上的 Pignistic概率，根據 LC原則選擇滿足條件的最優證據的線性規則問題可表示為：

其中，f（|A|）是|A|的增函數，度量了 A的不精確度；XA= m（A）表示決策變量。

定理1對LP問題如式（7）所示，當n=1時，最優解對應的非零決策變量只有兩個XA1和XΘ。

證明不妨設f（|A|）=|A|。設另一可行解包含不同于XA1和XΘ的非零決策變量 XB。若B?A1，則令（B）=0，（A1）=m（A1）+m（B），而 f（|A1|）（A1）+f（|B|（B）-（f（|A1|）m（A1）+f（|B|）m（B））=m（B）（|A1|-|B|）＞0，因此，該可行解不是最優解。若 B∩A1=Φ，則令（B）=0，，容易驗證這也是一組可行解，而 f（|A1|）（A1）+f（|B|）（B）+ f（|Θ|）（Θ）-（f（|A1|）m（A1）+f（|B|）m（B）+f（|Θ|）m（Θ））=m（B）（1+|A|-|B|）＞0，因此，該可行解不是最優解。對于B∩A1≠Φ、BA1的情形可類似證明。

下面結合數值實例說明這個方法的應用步驟。仍然考慮上面提到的例子。由樣本數據和 Bayes公式可得Jeffreys準則下參數λ的后驗概率密度為：

這是伽馬分布Ga（7，47 300）的核，即λ～Ga（r，Tr）= Ga（7，47 300），因此：

再由χ2分布的分位數，可得λ的1-α等尾置信區間為：

記此區間為［A（Tr），B（Tr）］，再由單調性，容易得可靠度 R（t0）=e-λt0的 1-α置信區間為：

取 α=0.1，當 r=7，Tr=47 300時，易查得（14）= 6.571，（14）=23.685，因此，參數 λ的0.90等尾置信區間為［6.946 089×10-5，2.503 700×10-4］；進而得到t0=500 h時的可靠度R（500）的0.90置信區間為［0.88，0.97］。

類似地，可推得在“共軛分布”思想下，t0=500 h時的可靠度R（500）的0.95置信區間為［0.87，0.95］。把由 Jeffreys準則下得到的可靠度置信區間［0.88，0.97］的置信度看作是 Pignistic概率，即 Bet P（［0.88，0.97］）=0.85。根據定理 1，滿足此 Pignistic概率的 LC-BBA的焦元區間只有［0.88，0.97］和［0，1］。因此，得方程組：

解得：

m1（［0，1］）=0.109 9，m1（［0.88，0.97］）=0.890 1

同理，把在“共軛分布”思想建立的可靠度置信區間［0.87，0.95］的置信度看作是Pignistic概率，即Bet P（［0.87，0.95］）=0.95。根據定理1，滿足此Pignistic概率的LCBBA的焦元區間只有［0.87，0.95］和［0，1］。因此，得方程組：

解得：

m2（［0，1］）=0.054 3，m2（［0.87，0.95］）=0.945 7

采用 Dempster證據組合規則對上面兩條證據進行融合，得到一個綜合的BBA：

m（［0.88，0.95］）=0.841 8，m（［0.87，0.95］）=0.103 9，m（［0.88，0.97］）=0.048 3，m（［0，1］）=0.006 0

利用Pignistic概率轉換公式可得可靠度的一個概率分布為：

在該方案下得到的 t0=500 h時該電子設備的可靠度的Pignistic概率密度函數如圖3所示。

將所得結果與在 Jeffreys準則下和“共軛分布”思想下得到的 t0=500 h時的可靠度的概率密度函數進行對比，如圖4所示。

圖3　Pignistic概率分布函數

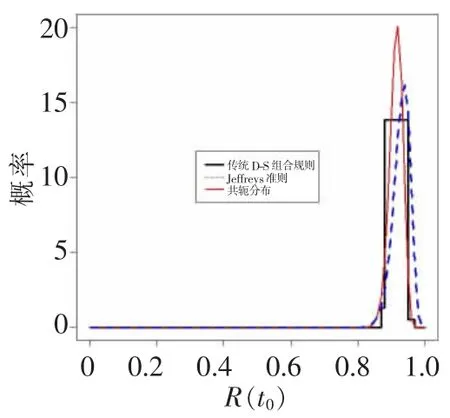
圖4　t0=500 h時指數分布可靠度的三種概率

3　結論

本文研究了 D-S證據理論在 Bayes可靠性評估中的應用方法。文中提出了兩種方法：（1）通過融合可靠性指標的后驗分布進行綜合評估；（2）通過融合可靠性指標的后驗置信區間進行綜合評估。數值實例表明，D-S證據理論在可靠性評估中會給出一個“謹慎”和“保守”的結論，這在對產品沒有足夠的先驗信息是有意義的。例如在大型客機、衛星、導彈等進行可靠性評估時，如果不能及時地檢測并避免故障，造成的損失是不可估量的。此時就需要對這些產品的可靠性進行一個“謹慎”的估計。因此，本文提出的評估方法適用于“對產品沒有充分的試驗信息”而“產品的故障能造成大的風險”的情況。

參考文獻

［1］楊露菁，余華.多源信息融合理論與應用［M］.北京：北京郵電大學出版社，2006.

［2］潘巍，王陽生，楊宏戟.Pignistic概率轉換算法設計［J］.計算機工程，2005，31（4）：20-22.

［3］DUBOISD，PRADEH.Theprincipleof minimum specificity as a basis for evidential reasoning［J］.Uncertainty in Knowledge-Based Systems，Lecture Notes in Computer Science，New York：Springer-Verlag，1987，286：75-84.

［4］RISTIC B，SMETS P.Target classification approach based on the belief function theory［J］.IEEE Transactions on Aerospace and Electronic Systems，2005，41（2）：574-583.

App lication of evidence theory in Bayes reliability assessment

Ma Lina
（Department of Information，College of Xingzhi，Xi′an University of Finance and Economics，Xi′an 710038，China）

In order to express and apply better the uncertain prior information，this paper presents a new Bayesian reliability assessment scheme based on the D-S evidence theory.The estimation for reliability index of exponential distributions is studied for the non-replacement fixed failure number test samples.It proposes two reliability assessment methods.One is a comprehensive evaluation by integrating the posterior distributions of reliability indices.The other is one by integrating the posterior confidence intervals.Numerical examples show that the proposed method is prudent and reasonable.

D-S evidence theory；Bayesian methods；reliability；LC guideline；Pignistic probability

O213.2

A

1674-7720（2015）06-0062-03

2014-11-30）

馬麗娜（1986-），女，碩士研究生，主要研究方向：圖像處理與信息整合。