基于LS-SVM的織物烘干含水率模型的應用

趙迪, 金福江, 葉斌

(華僑大學信息科學與工程學院,福建廈門361021)

基于LS-SVM的織物烘干含水率模型的應用

趙迪, 金福江*, 葉斌

(華僑大學信息科學與工程學院,福建廈門361021)

針對織物烘干過程中工藝參數設定把握不準,導致織物過烘或未烘透造成能源浪費或織物質量下降的問題,分別采用多元非線性回歸、擴展的GM(1,1)、最小二乘支持向量機建立織物干燥過程中的含水率預測模型,并通過實驗驗證方法的有效性。實驗結果表明,相對于其他兩種模型,基于最小二乘支持向量機的含水率預測模型可以準確學習織物干燥過程中的非線性關系,預測值平均誤差低至1.8%。因此,該模型是準確的,可以為烘干環節生產工藝的選取提供依據。

織物烘干;含水率;預測;建模;最小二乘支持向量機

作為印染過程的重要一環,織物烘干的目的是使高溫固色織物的濕度低于纖維臨界含水率[1]。傳統印染企業通常依靠經驗對織物烘燥過程工藝參數進行人為設定,但這樣往往造成織物過度烘燥或者未烘透,容易導致浪費能源或對織物手感、懸垂性產生影響。因此,研究烘干工藝參數與織物下機含水率之間關系的數學模型,并建立含水率變化的預測模型以及工藝參數優化模型,成為印染企業亟待解決的問題。

在干燥模型方面,諸愛士[2]、劉顯茜等[3]及高波等[4]分別研究了熱風干燥時茭白、胡蘿卜、紅棗等的水分比隨時間變化的關系模型,但都只針對溫度固定時含水率隨時間變化的情形,并未考慮烘干溫度、初始含水率及生產實踐中超喂率對烘干過程的影響。為此,文中將初始含水率、溫度、超喂率及烘干時間作為系統輸入,將最終含水率作為系統輸出,利用多元非線性回歸、擴展的GM(1,1)灰色預測、最小二乘支持向量機(LS-SVM)建立織物烘干過程中多種工況下的含水率預測模型,利用不同模型間對比以及同模型不同優化參數的對比給出最優模型,并通過實驗驗證模型的有效性。

1 織物烘干過程簡述

烘干過程中,將織物通過軋車、拉幅架等機械裝置平鋪于網帶上,由傳動裝置帶動織物進入烘燥機并在循環熱風上下交錯的噴吹下無張力波曲狀前進,最終達到烘干的目的。可見,影響織物干燥狀態的主要因素為循環熱風的溫度、噴風速度[5-6]以及網帶的行進速度(等價干燥時間)。由于噴風速度受限于烘干機,故不予考慮。另外,為保證織物經緯向充分收縮以降低縮水率,一般會使織物以一定超喂進入烘燥機,超喂影響水分轉移速度以及表面水分汽化速度。因此,選取

輸入特征向量 X=(x1,x2,x3,x4),

輸出特征向量 Y=(y)。

其中,x1,x2,x3分別為實驗條件中的初始干基含水率、溫度、超喂率;x4為采樣時間;y為下機含水率。織物烘干的工作原理如圖1所示。

圖1 織物烘干的工作原理示意Fig.1 W orking princip le of fabric drying

2 織物含水率預測模型建立

在Rapid烘干定型機上,以純棉雙面布為實驗對象,以初始干基含水率0.6～1.5,烘干溫度80～160℃,超喂率-0.2～0.6為實驗條件,通過控制變量法共設計27大組實驗,實驗條件取值的空間分布如圖2所示。根據GB/T9995—1997含水率測定法取20 s(織物失重為最終失重98%時所需時間的20%,實驗條件不同應取間隔不同,為統一選擇各個條件下應取的最短間隔20 s)為時間間隔,當相鄰兩次烘干質量變化小于0.1%時,停止烘干。將測得的含水率作為輸出,每測一次作為一組數據,共計得290組數據。所有數據中選200組用于模型的擬合或者訓練,其余90組用于模型測試。

圖2 實驗條件取值的空間分布Fig.2 Distribution of the experim ental condition in the space

2.1 多元非線性模型建立

首先建立輸出與各輸入的單元非線性回歸模型,再依次選擇合適的多元非線性回歸模型(Multiple Non-linear Regression,MNLR),模型如下:

2.2 GM(1,1)預測模型

由于GM(1,1)為輸出關于時間的1階單變量模型,因此對于多變量系統需要擴展后使用,將擴展后的GM(1,1)模型稱為EGM(Extending Grey Model)。

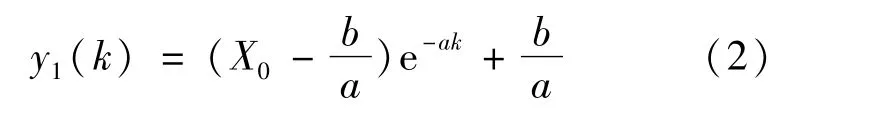
2.3 基于LS-SVM的預測模型

建立LS-SVM模型,首先對原始數據進行預處理,消除不同變量取值范圍間的巨大懸殊;構建數據樣本,選擇合適的核函數,將學習樣本輸入支持向量機訓練;采用交叉驗證法優化參數,獲得輸入輸出的精確映射關系;最后輸入測試樣本獲取模型誤差[7-10]。具體建模流程如圖3所示。

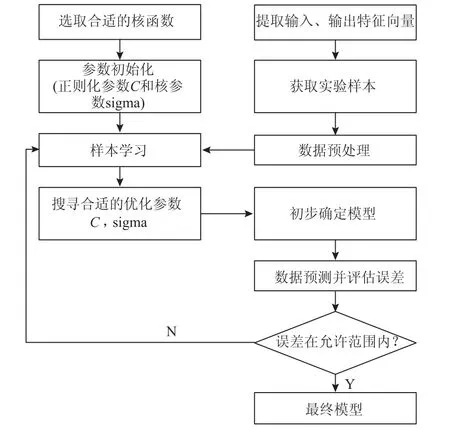
圖3 LS-SVM建模流程Fig.3 Flow chart of the LS-SVM m odeling

最終確立模型如下:

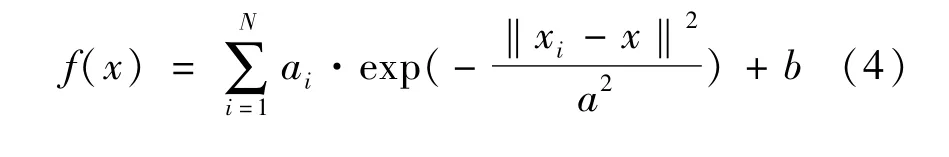
3 模型有效性分析及驗證

3.1 3種模型預測效果對比

將290組數據全部納入考查范圍,以擬合優度R2和均方根誤差RMSE(Root Mean Square Error)為評價指標,對比多元非線性模型、GM(1,1)預測模型和基于LS-SVM的預測模型的整體擬合效果。3種不同模型的性能對比見表1。其中

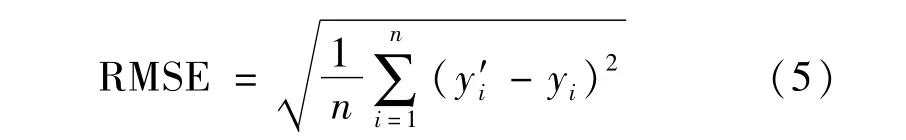
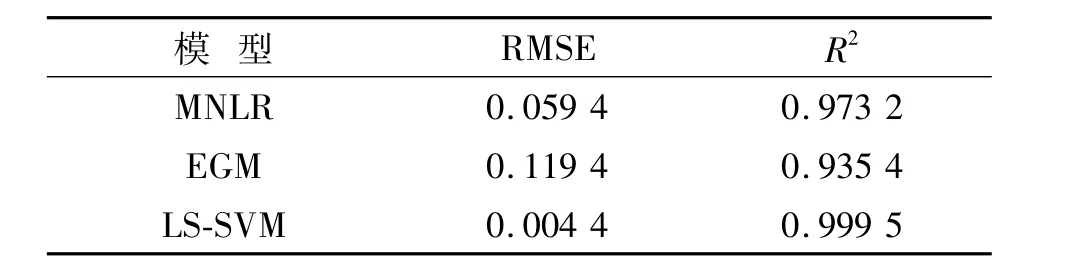
表1 3種模型性能對比Tab.1 Com parison o f them odels’p roperty

由表1可以看出,基于LS-SVM的預測模型的擬合優度最接近1,且均方根誤差最接近0。由此可見, LS-SVM模型的回歸效果明顯好于其他兩種,MNLR次之,EGM預測模型整體效果最差。為更具體對比3種模型預測效果,隨機選擇一種實驗條件,以初始含水率x1=1.027,溫度x2=80℃,超喂率x3=0.6為例,觀察隨著烘干過程的進行3種模型的跟蹤效果,并利用下式計算相對誤差。

3種模型的跟蹤效果如圖4所示。

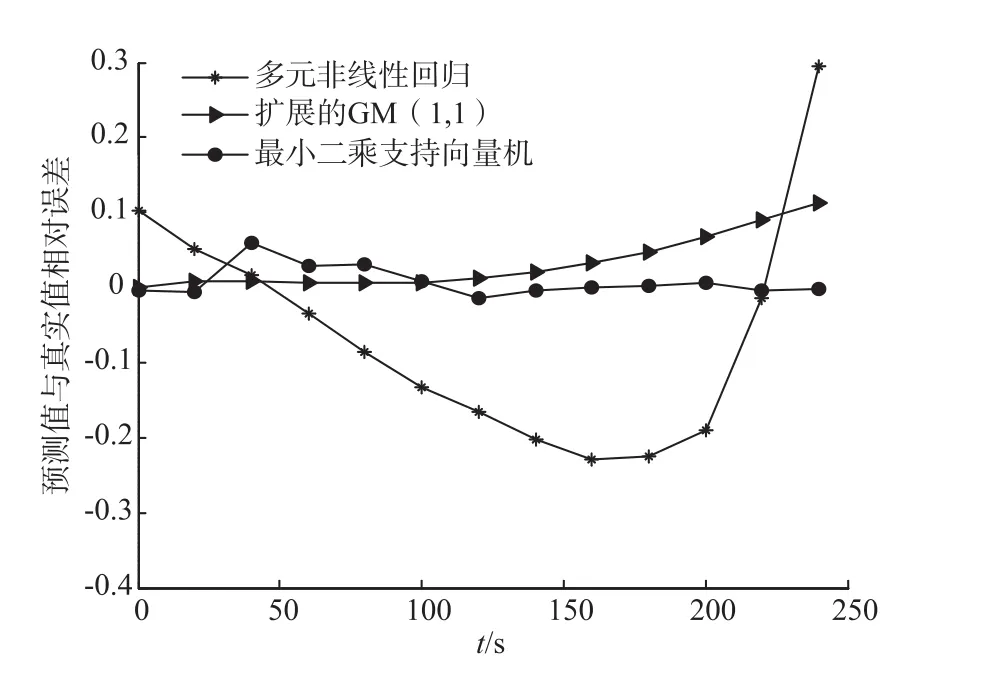
圖4 3種模型跟蹤效果對比Fig.4 Com parison of threemodels’tracking effects

由圖4可見,LS-SVM預測模型表現出良好的預測效果,相對誤差一直穩定于0附近;而擴展的GM(1,1)模型在烘干開始之初表現良好,但隨著烘干過程的推進,預測值逐漸漂移,越來越偏離真值。這與EGM模型本身的建模方法有關,因它是根據幾個初始時間序列預測后續時間序列取值,故當預測點與已知的建模數據時間點靠近時預測較精準,后續時間點預測誤差很大;而多元分線性模型的預測誤差表現出較強的隨機性,無規律可言。

3.2 不同核函數的LS-SVM性能對比

為選擇合適的LS-SVM核函數,分別采用高斯徑向基(RBF)、多項式、線性函數為核函數,輸入模型進行訓練,并采用交叉驗證法優化模型參數,將得到的測試樣本的預測值分別與實驗值比較,得到圖5所示的對比圖。

由圖5可以看出,采用RBF和多項式核函數的LS-SVM模型獲得良好的預測效果,線性核函數的實驗模型出現明顯偏差。為進一步對比3種模型整體的擬合效果,給出模型擬合優度和均方誤差,具體見表2。

由表2可見,在參數選擇合適的前提下,采用RBF核函數和多項式核函數可以達到相似的擬合效果;采用RBF核函數模型性能略好;以線性函數為核函數的模型泛化能力較差。對于文中含水率預測模型系統內存在的復雜的非線性關系,采用線性函數的LS-SVM模型明顯不適用。

3.3 參數優化前后模型性能對比

采用交叉驗證法為模型選擇合適的優化參數,以均方根誤差RMSE、擬合優度R2、平均誤差為指標對比參數優化前后模型的預測效果(見表3所示)。其中,平均誤差按下式計算。

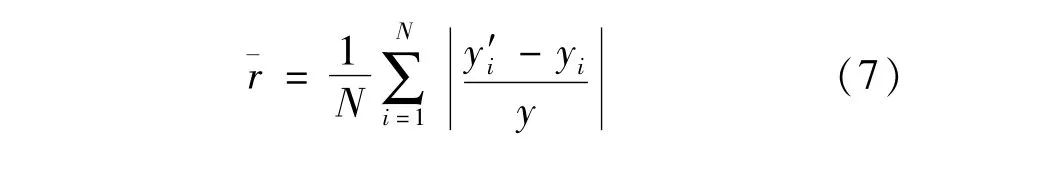
圖5 3個不同核函數的LS-SVM模型預測值與實驗值對比Fig.5 Com parison between predictive values and experimental ones of three LS-SVM models for different kernel functions

表2 3個不同核函數的LS-SVM模型性能對比Tab.2 Com parison of the LS-SVM m odel perform ance for d ifferent kernel functions

表3 LS-SVM模型參數優化前后效果對比Tab.3 Com parison of the model parameters optim ization effect

由表3可見,平均預測誤差減少4.9%,優化效果明顯,也彰顯參數(C,σ2)取值對于模型回歸效果的重要作用。

4 結 語

通過MNLR,EGM,LS-SVM 3種模型的性能對比以及LS-SVM不同核函數、參數的模型性能對比,可得出以下結論:

1)相比MNLR和EGM,LS-SVM方法有較強的非線性關系學習能力和良好的泛化能力;

2)在LS-SVM模型核函數的選擇上,只要參數優化得當,采用RBF和多項式核函數模型可以達到相似的性能;

3)對于文中的含水率預測模型,以RBF為核函數的LS-SVM預測模型為最佳選擇;

4)基于LS-SVM的含水率預測模型,擬合優度99.95%,平均預測誤差1.8%,可以用于生產實踐中的含水率預測,并為烘干過程中的工藝參數設計提供有效參考。

另外,文中仍有諸多欠缺之處,如未能給出SVM正則化參數和核參數的選定方法,只能是逐點搜索尋找最優;只是給出織物含水率的預測模型,未繼續探究如何根據含水率變化情況逆向求解烘干過程工藝參數。對以上問題的彌補可成為今后的努力方向。

[1]陳立秋.連續軋染設備的技術進步[J].印染,2004(10):35-38.

CHEN Liqiu.Progresses in continuous pad dyeing equipment[J].Dyeing and Finishing,2004(10):35-38.(in Chinese)

[2]諸愛士.茭白片熱風對流干燥模型與傳質性能[J].高校化學工程學報,2012,26(3):541-546.

ZHU Aishi.Themodel and mass transfer performance of convective hot air drying of water-oat slices[J].Journal of Chemical Engineering of Chinese Universities,2012,26(3):541-546.(in Chinese)

[3]劉顯茜,陳君若,劉美紅,等.胡蘿卜對流干燥過程理論分析——臨界水分質量比[J].化學工程,2012,40(9):34-37,47.

LIU Xianxi,CHEN Junruo,LIU Meihong,et al.Theoretical analysis of convective drying process of carrot-critical:moisturemass ratio[J].Chemical Engineering,2012,40(9):34-37,47.(in Chinese)

[4]高波,吳文福,楊永海.一種薄層干燥新模型的建立[J].農業機械學報,2003,34(3):55-57.

GAO Bo,WUWenfu,YANG Yonghai.Development of a new thin-layer drying model[J].Transactions of the Chinese Society of Agricultural Machinery,2003,34(3):55-57.(in Chinese)

[5]朱冬林,王磊.合成纖維織物和棉織物熱風干燥特性的實驗研究[J].東華大學學報:自然科學版,2003,29(1):81-84.

ZHU Donglin,WANG Lei.Experimental research on convection drying characteristics of synthetic fibre and cotton fabrics[J]. Journal of Donghua University:Natural Science,2003,29(1):81-84.(in Chinese)

[6]凌群民,譚磊.織物干燥機理及干燥速率的探討[J].紡織學報,2006,27(8):22-24.

LING Qunmin,TAN Lei.Investigation on the principle and the rate of fabric drying[J].Journal of Textile Research,2006,27 (8):22-24.(in Chinese)

[7]鐘麗瑩,金福江.基于LS-SVM的棉/氨彈力布熱定型效率[J].武漢理工大學學報:信息與管理工程版,2010,32(1)88-90,95.

ZHONG Liying,JIN Fujiang.Heat-setting efficiencymodel of cotton-spandex knitgoods based on LS-SVM[J].Journal ofWuhan University of Technology:Information and Management Engineering,2010,32(1)88-90,95.(in Chinese)

[8]葉蔚,王時龍,雷松.支持向量機刀具磨損預測模型及Matlab仿真[J].工具技術,2009,43(10):42-45.

YEWei,WANG Shilong,LEI Song.Predicting model of cutting tool wear based on least squares support vector machine and Matlab simulation[J].Tool Engineering,2009,43(10):42-45.(in Chinese)

[9]孫涵,楊普容,成金華.基于Matlab支持向量回歸機的能源需求預測模型[J].系統工程理論與實踐,2011,31(10): 2001-2007.

SUN Han,YANG Purong,CHENG Jinhua.Forecastingmodel of energy demand based on Matlab support vector regression[J]. Systems Engineering Theory and Practice,2011,31(10):2001-2007.(in Chinese)

[10]閻威武,邵惠鶴.支持向量機和最小二乘支持向量機的比較及應用研究[J].控制與決策,2003,18(3):358-360.

YANWeiwu,SHAO Huihe.Application of support vector machines and least squares support vector machines to heart disease diagnoses[J].Control and Decision,2003,18(3):358-360.(in Chinese)

(責任編輯:邢寶妹)

Research and App lication of Fabric M oisture Content M odel Based on LS-SVM

ZHAO Di, JIN Fujiang*, YE Bin
(College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China)

It is hard to grasp the parameter setting in the fabric drying process,which will cause over-drying or under-drying,and lead to energy waste or the decreasing of the quality.To solve this problem,this paper,uses the multivariate non-linear regression,extended GM(1,1)and the least squares support vector machines(LS-SVM)to establish the prediction model of moisture content(dry base)during the drying process,then draws the conclusion through experiments that compared with other twomodels,the least squares based support vectormachinemodel could effectively learn the non-linear relationship in the drying process for predicting moisture content,and the average prediction accuracy is as low as 1.8%.As a result,LS-SVM could effectively predictmoisture content and provide theoretical basis for the selection of production parameters in the actual drying process.

fabric drying,moisture content,prediction,modeling,LS-SVM

TP 18;TS 115.1

A

1671-7147(2015)01-0006-05

2014-08-01;

2014-09-16。

國家自然科學基金項目(61143005);福建省產學研重大專項項目(2011H5019);福建省泉州市科技計劃重點項目(2011G8)。

趙迪(1991—),女,河南商丘人,電氣工程專業碩士研究生。

*通信作者:金福江(1965—),男,新疆烏魯木齊人,教授,博士生導師。主要從事復雜系統建模、優化與控制等研究。

Email:jinfujiang@163.com