非自治二階哈密頓系統周期解的存在性

石璐, 安天慶

(河海大學理學院,江蘇南京210098)

非自治二階哈密頓系統周期解的存在性

石璐, 安天慶*

(河海大學理學院,江蘇南京210098)

用最小作用原理和臨界點理論研究了一類非自治二階哈密頓系統周期解的存在性問題。首先假設F(t,x)=F1(t,x)+F2(t,x)滿足假設(A),再使F1滿足次凸條件,并且在[0,T]上的積分趨于無窮,運用最小作用原理,得到一個解的新的存在性結果。另外,將F1在[0,T]上的積分趨于無窮這一條件減弱為F1在[0,T]的一個正測度子集E上的積分趨于無窮,運用最小作用原理,也能得到同樣的結果。

次凸位勢;周期解;臨界點;最小作用原理

考慮非自治二階哈密頓系統

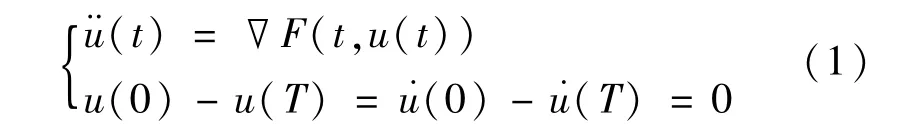
周期解的存在性問題。其中T＞0,且F:[0,T]× RN→R滿足下述假設:(A)對每個x∈RN,F(t,x)關于t可測,對a.e.t∈[0,T],F(t,x)關于x連續可微,且存在a∈C[R+,R+],b∈L1([0,T];R+),使得

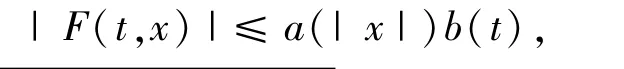
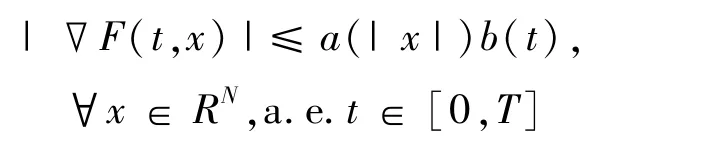
很多學者已經用最小作用原理證明了問題(1)至少有一個解,且為φ在上的最小值。文中受到文獻[1-4]中結果與文獻[5-7]中條件的激發,考慮了問題(1)中的次凸問題,同樣通過運用最小作用原理,得到問題(1)的解的新結果。文中假設F(t,x)=F1(t,x)+F2(t,x)滿足假設(A)。

1 主要結果

定理1 假設F1,F2滿足假設(A),且

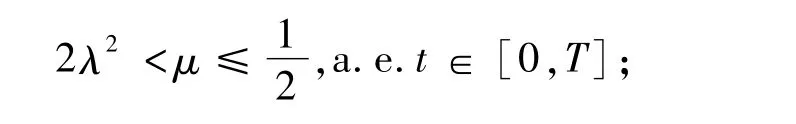
(2)?r∈L1(0,T;R+),α∈[0,2),且

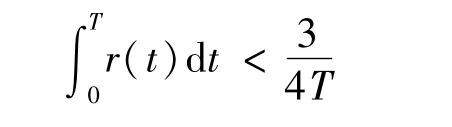
使得

注[2]若對于λ,μ＞0,x,y∈RN,有

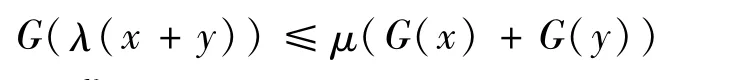
稱函數F:RN→R為(λ,μ)次凸。

定理2 假設F1,F2滿足假設(A),且

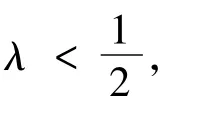
(2)?r∈L1(0,T;R+),α∈[0,2),且

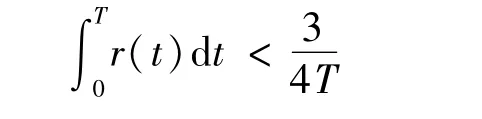
使得

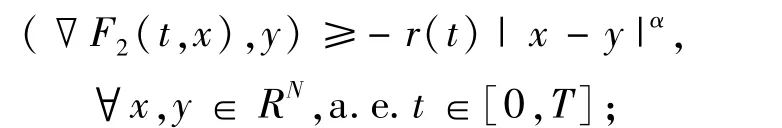
(3)?E?[0,T],且meas(E)＞0,使得

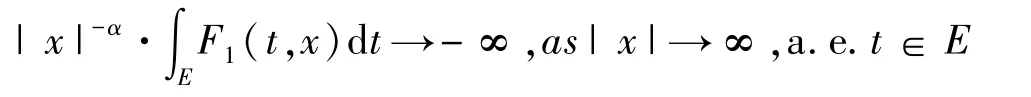
并且?γ∈L1(0,T),使得

則問題(1)至少有一個解,且為φ在H1T(Ω)上的最小值。

2 定理的證明

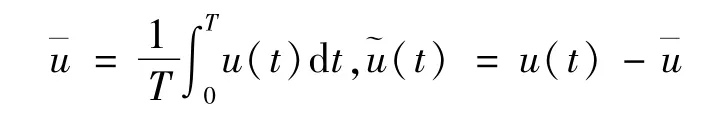
從而有Sobolev不等式和Wirtinger不等式:

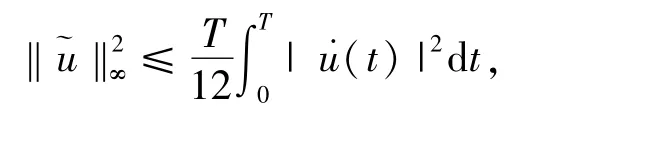
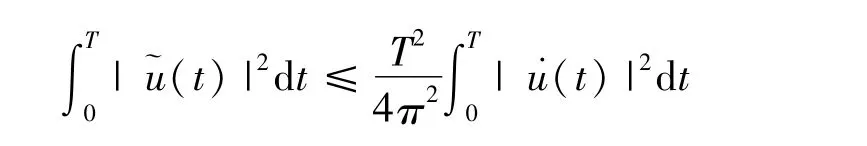
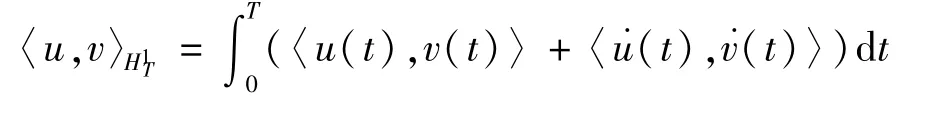
則對應的范數為

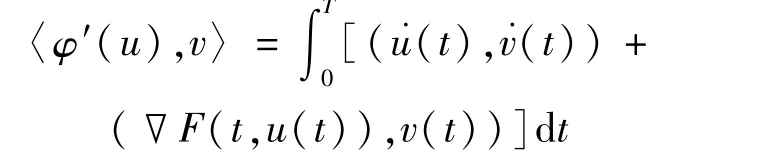
易知問題(1)的解即為φ的臨界點。

由文獻[1]可知,該泛函是下半弱連續的,因為強制的下半弱連續泛函必有最小值點,所以證明定理1和定理2時,只考慮泛函的強制性。

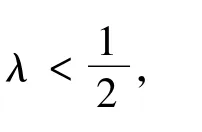
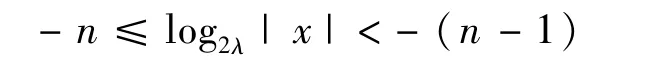
則由(2λ)-(n-1)＜|x|≤(2λ)-n,有

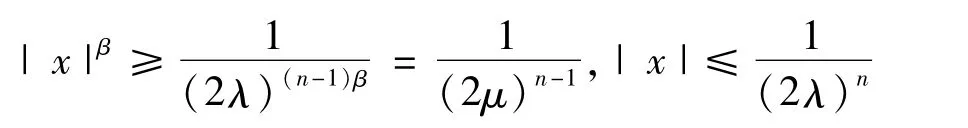
所以由條件(1)和假設(A),對于a.e.t∈[0,T]和所有的|x|≥1,有

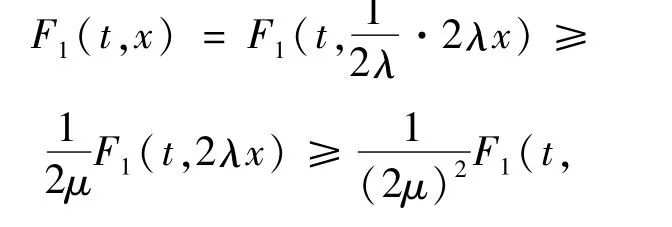
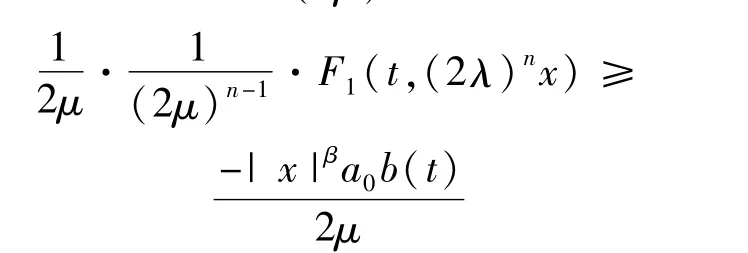
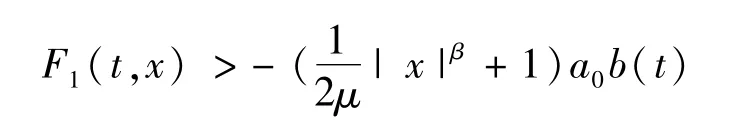
其中β＜2。

又F1(t,·)是(λ,μ)次凸,則

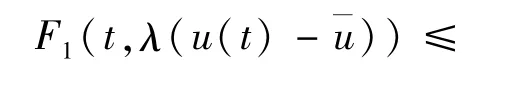
其中a0=max0≤s≤la(s)。

進一步,知道對于a.e.t∈[0,T]和所有的x∈RN,有

即

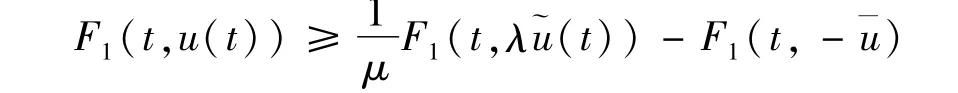
由條件(1)和Sobolev不等式,有

其中c1,c2均為正常數。

由條件(2),知道

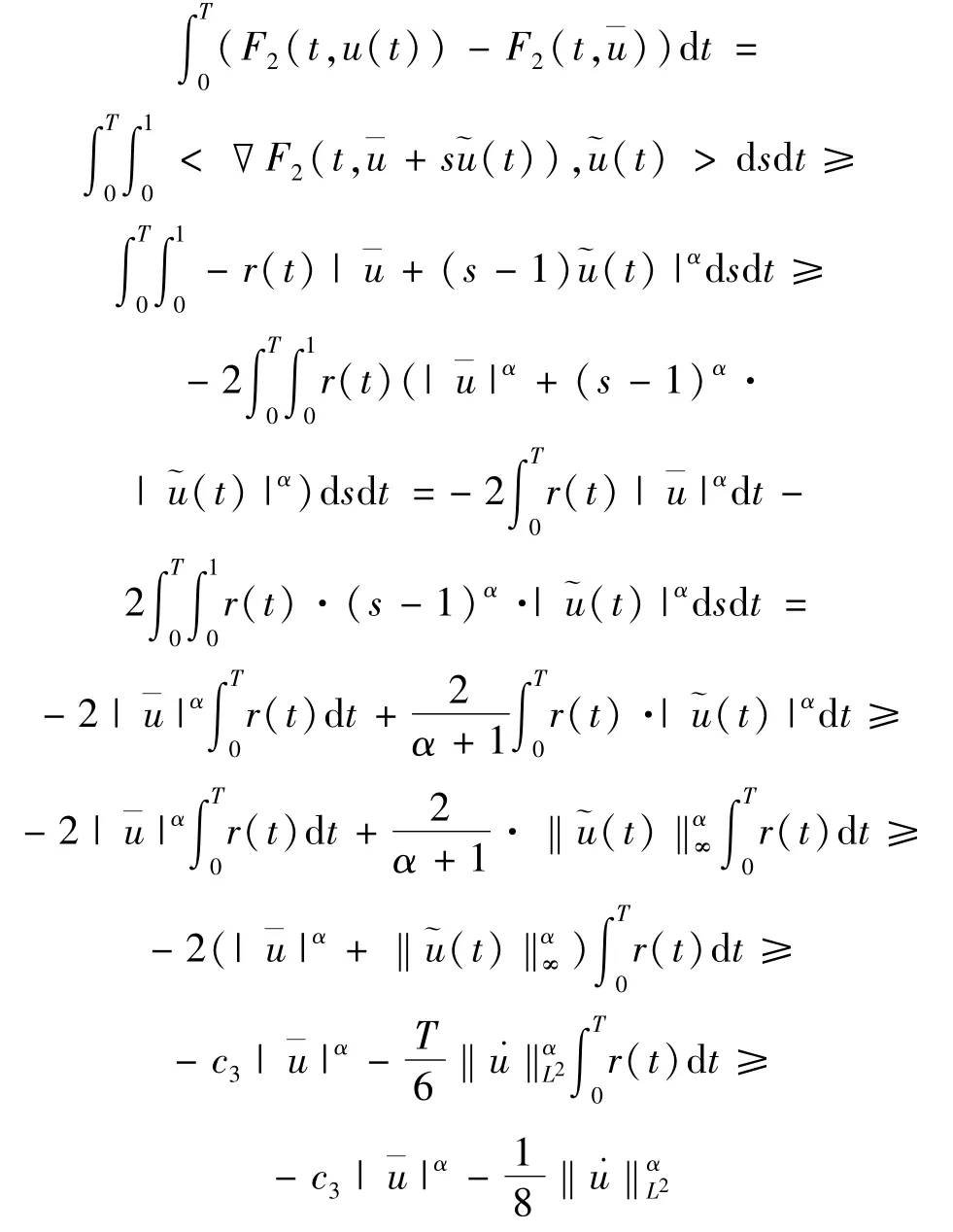
所以

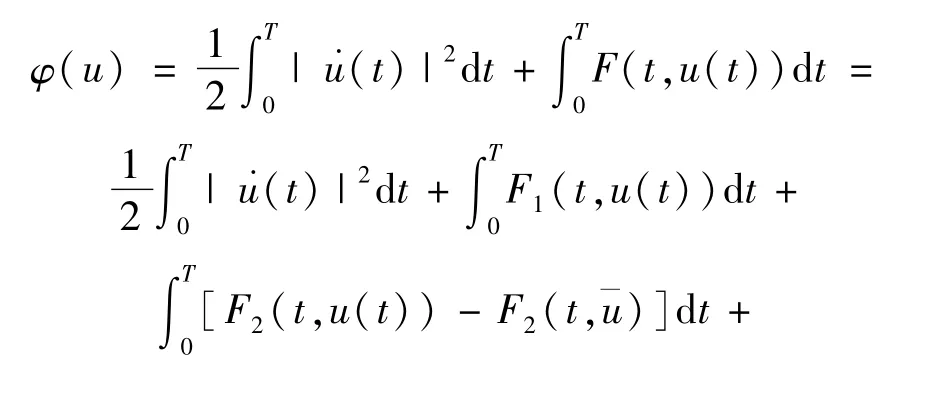
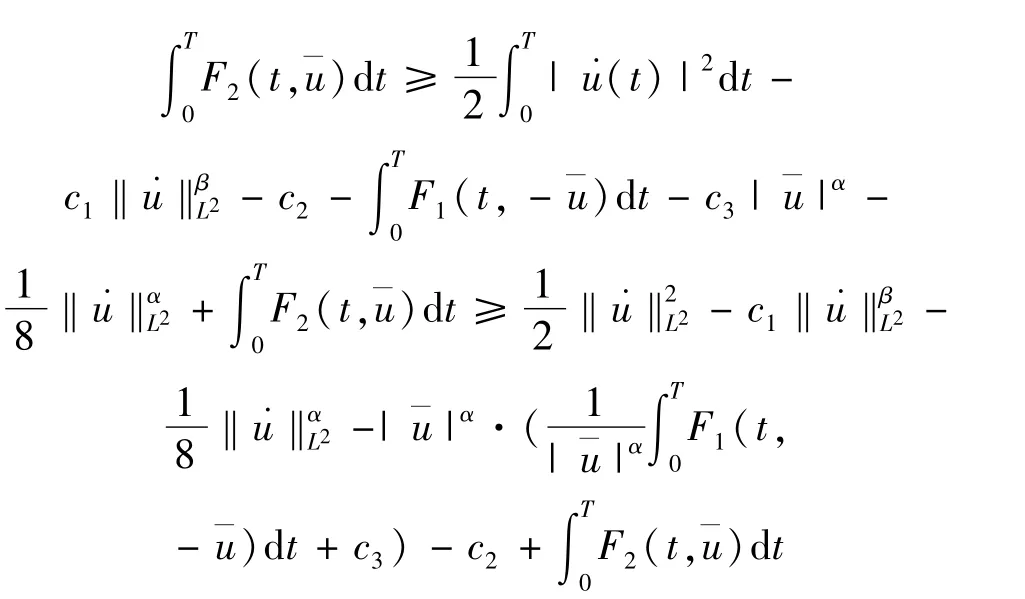
由于

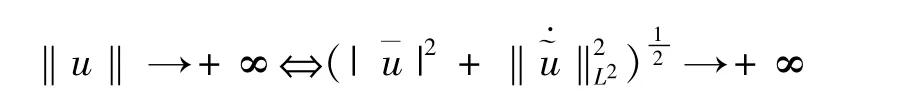
則由條件(3),β＜2,α∈[0,2),知道

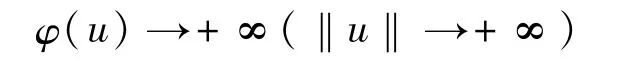
證畢。

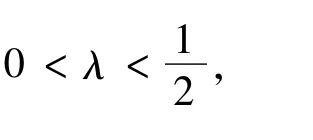
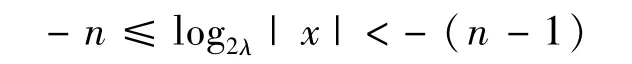
則由(2λ)-(n-1)＜|x|≤(2λ)-n,有

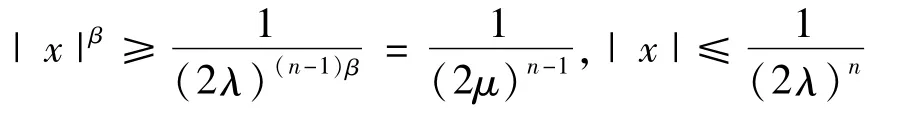
所以由條件(1)和假設(A),對于a.e.t∈[0,T]和所有的|x|≥1,有

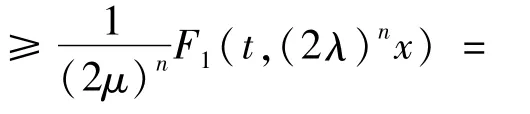
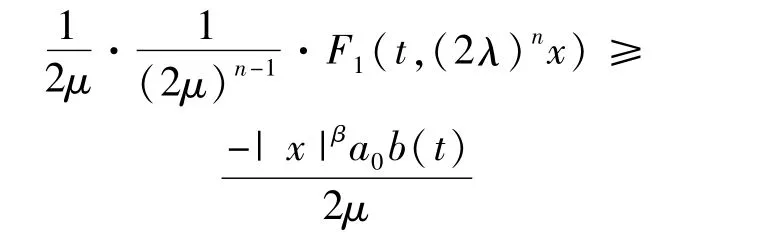
其中a0=max0≤s≤la(s)。

進一步,知道對于a.e.t∈[0,T]和所有的x∈RN,有

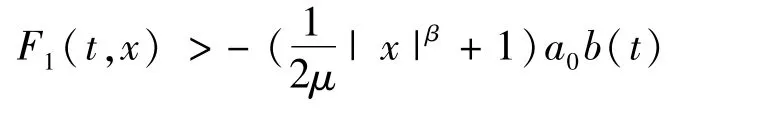
其中β＜2。

又F1(t,·)是(λ,μ)次凸,則

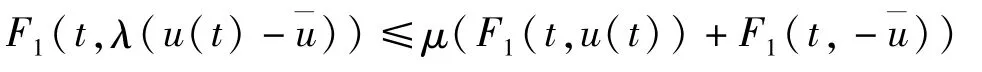
即

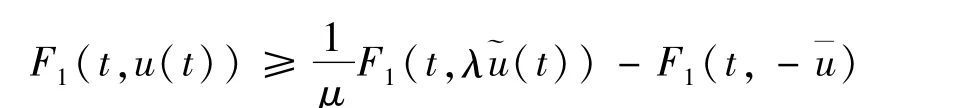
由條件(1)和Sobolev不等式,有

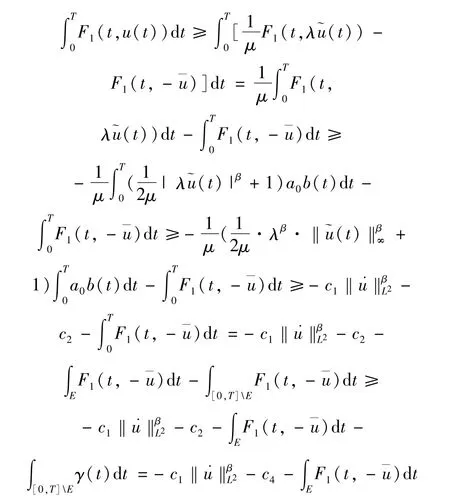
其中c1,c2,c4均為正常數。

由條件(2),知道

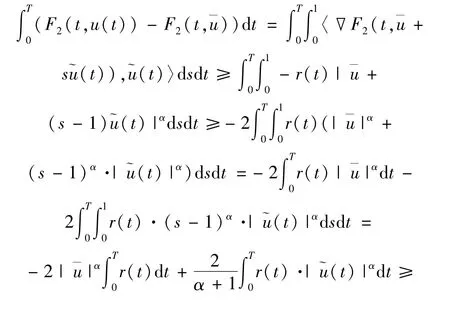
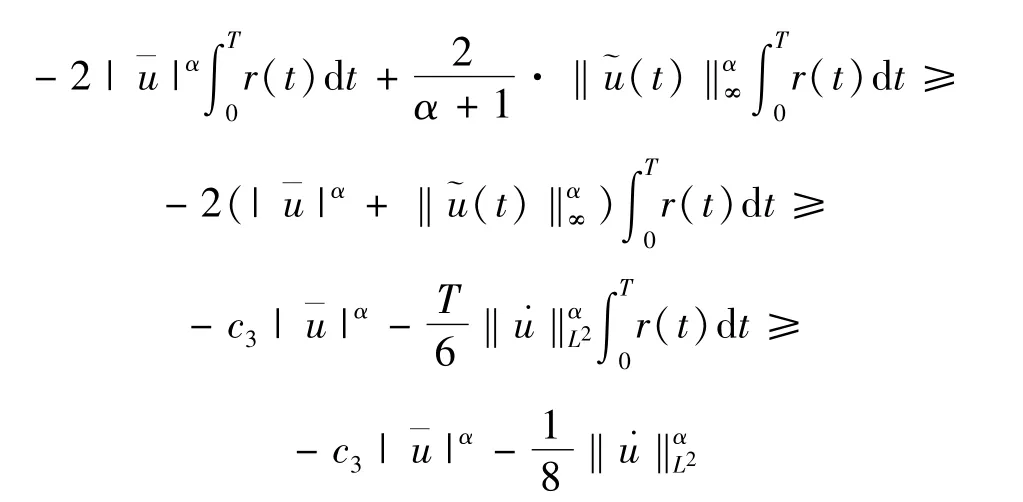
從而

由于

則由條件(3),β＜2,α∈[0,2),知道

證畢。

[1]Mawhin J,Willem M.Critical Points Theory and Hamiltonian Systems[M].New York:Springer-Verlag,1989.

[2]WU Xingping,TANG Chunlei.Periodic solutions of a class of nonautonomous second order systems[J].JMath Anal Appl,1999, 236:227-235.

[3]孟鳳娟.一類二階哈密頓系統周期解的存在性[J].河南科學,2010,28(1):21-24.

MENG Fengjuan.Existence of periodic solutions for a class of second order Hamiltonian systems[J].Henan Science,2010,28 (1):21-24.(in Chinese)

[4]ZHAO Fukun,WU Xian.Periodic solutions of a class of nonautonomous second order systems[J].JMath Anal Appl,2004,296: 422-434.

[5]Nurbek Aizmahin,AN Tianqing.The existence of periodic solutions of nonautonomous second order Hamiltonian systems[J]. Nonlinear Analysis,2011,74:4862-4867.

[6]MA Jian,TANG Chunlei.Periodic solutions for some nonautonomous second order systems[J].JMath Anal Appl,2002,275:482-494.

[7]TANG Chunlei.Periodic solution of nonautonomous second order systems[J].JMath Anal Appl,1996,202:465-469.

(責任編輯:楊 勇)

Existence of Periodic Solutions for Nonautonom ous Second O rder Ham iltonian System

SHILu, AN Tianqing*
(College of Science,Hohai University,Nanjing 210098,China)

By using the least action principle and the critical point theory,this paper studies the existence of the periodic solutions for a class of non-autonomous second-order Hamiltonian systems.First,assuming that F(t,x)= F1(t,x)+F2(t,x)satisfies hypothesis(A),then F1meets the subconvex condition,and the integration tends to infinity in[0,T],we can obtain a new existence theorem by using the leastaction principle.Moreover,weweaken the condition that the integration of F1tends to infinity in[0,T]to the case that the integration of F1tends to infinity in a positive measure subset E of[0,T],we can get the same result by using the least action principle.

subconvex potential,periodic solutions,critical points,the least action principle

O 177

A

1671-7147(2015)01-0117-04

2014-09-12;

2014-09-25。

河海大學中央高校業務費項目(B12020128)。

石璐(1990—),女,江蘇淮安人,基礎數學專業碩士研究生。

*通信作者:安天慶(1963—),男,甘肅古浪人,教授,博士生導師。主要從事非線性泛函分析等研究。

Email:antq@hhu.edu.cn