三角形截面鋼管桁架人行橋人致振動舒適度評價

朱高波 童金虎

摘 要：結構輕柔的人行橋受行人激振后會產(chǎn)生不同程度的振動，當振動響應達到一定程度時，就可能使橋上行人感到不適甚至引發(fā)恐慌。如何評估這種振動并將其控制在可接受的范圍之內(nèi)，是人行橋設計過程中需要考慮的一個問題，但國內(nèi)規(guī)范對人行橋的人致振動舒適度尚無明確的評價標準。文章以一座結構新穎的鋼桁架人行橋為例，介紹了《德國人行橋設計指南》對人行橋舒適度進行評價的方法，并提出了成橋?qū)嶒灲ㄗh。

關鍵詞：人行橋；振動；時程分析法；舒適度

中圖分類號：U441.3 文獻標識碼：A 文章編號：1006-8937（2015）08-0146-02

隨著我國橋梁技術的進步，各種結構新穎的大跨徑人行橋不斷涌現(xiàn)，而隨著橋梁跨徑的逐步增加，結構剛度隨之降低，人行橋的人致振動問題也日漸突出。人行橋的人致振動雖然會在一定程度上增加結構的荷載效應，但總的來說基本上還是一個舒適性的問題。關于人行橋的振動及舒適性問題，我國相關規(guī)范有“天橋上部結構豎向自振頻率≥3 Hz”的規(guī)定。一般來說，將橋梁剛度提高到4倍才能使自振頻率提高一倍，因此大跨度人行橋的自振頻率要達到“≥3 Hz”這一標準是比較困難且很不經(jīng)濟的。我國現(xiàn)行人行橋設計規(guī)范在人致振動響應及行人舒適性的規(guī)定方面還有待完善。隨著2000年英國千禧橋在開通當日發(fā)生的過度橫向振動事件引起廣泛關注，一些西方發(fā)達國家對大跨人行橋的人致振動理論及工程應用的研究已經(jīng)走在了前列。德國人行橋設計指南（EN03，2007）（下文簡稱“德國指南”）在人行橋的舒適性評價方面已有較完整的規(guī)定。本文結合工程實際，依據(jù)德國指南，對一座較大跨徑的三角形截面鋼桁架人行橋的人致振動舒適度進行分析評價。

1 工程概述

1.1 總體布置

本橋由計算跨徑為68.4 m的簡支鋼桁架主橋及兩側(cè)坡比為1？誜8的推行坡道引橋組成，橋面全寬5 m，橋梁全長164.83 m。橋型總體布置如圖1所示。

主橋桁架的橫斷面呈三角形，如圖2所示。該結構是在常規(guī)下承式鋼桁架的基礎上將兩片主桁的上弦桿退化成一根上弦桿，取消了上平縱聯(lián)，并將下弦桿間距適當拉開，在增強了桁架橫向剛度的同時使橋面凈空滿足設計要求。該結構在縱向及橫向均采用穩(wěn)定的“三角形”構造，造型簡潔，力學概念清晰，自重較輕而結構剛度相對較大。

1.2 主橋上部結構

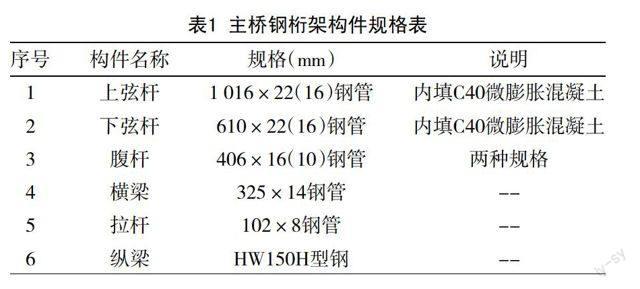
主橋桁架結構由上弦桿、下弦桿、腹桿、橫梁、縱梁、下弦平面拉桿等組成，桁架計算高度為8.2 m，寬度為8.2 m，縱向節(jié)點間距7.6 m。上、下弦桿內(nèi)灌填混凝土以提高橋梁整體剛度及鋼管節(jié)點承載力。鋼筋混凝土橋面板通過剪力鍵與桁架縱梁結合，結構厚度為12 cm，鋪裝厚度2.75～5 cm。主橋桁架主要構件均采用Q345C材質(zhì)，構件規(guī)格詳見表1。

2 動力特性分析

2.1 建模及假定

采用MIDASCIVIL2013有限元程序建模進行動力特性分析。上下弦桿內(nèi)填充混凝土對提高結構剛度有一定效果，當完全計入上、下弦桿內(nèi)所填充混凝土的剛度時，結構的基頻可提高到2.4 Hz以上。考慮到鋼管混凝土施工質(zhì)量的不確定性，本次結構建模時偏安全的將上、下弦桿內(nèi)填充的混凝土僅作為荷載考慮，不計結構剛度；12 cm厚的混凝土橋面板考慮結構剛度，而其上的鋪裝及欄桿僅作為荷載考慮，不計結構剛度。本橋結構自重較小，活載與恒載的比值相對較大，因此動力特性分析時，按照1.5人/ m2的分布密度（單人體重按80 kg計）考慮了行人荷載。上述荷載在動力特性分析時均轉(zhuǎn)化為質(zhì)量考慮。

2.2 動力特性分析結果

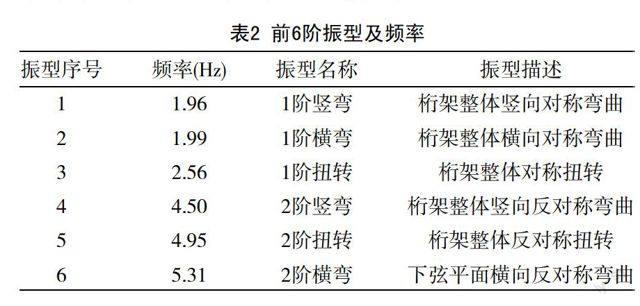
根據(jù)上述假定，對主橋上部結構進行動力特性分析，得到結構前6階模態(tài)的頻率及振型描述，見表2。

3 振動舒適性評價

當人行橋的固有頻率范圍在臨界范圍之內(nèi)時，需要對人行橋的舒適性進行評價。德國指南采用人致振動最大加速度響應來評價人行橋的舒適度。最大加速度的計算可采用單自由度法、響應普法及有限元法等，本文采用有限元法進行計算。

3.1 舒適度驗算的臨界范圍

人行橋豎向及縱向振動的敏感頻率范圍為1.25～2.3 Hz，橫向振動的敏感頻率范圍為0.5～1.2 Hz。

另外，二階行人諧波荷載也可能激發(fā)人行橋豎向振動（橫向振動則不受影響）。因此人行橋舒適度驗算的頻率范圍擴展為：豎向及縱向振動1.25～4.6 Hz，橫向振動0.5～1.2 Hz。當人行橋的自振頻率不在上述敏感頻率范圍時，一般可認為人行橋的人致振動問題自然滿足要求。結合表2的動力特性分析結果，本橋第1、4階振型主要表現(xiàn)為豎向振動，頻率分別為1.96/4.5 Hz，應進行豎向振動的舒適度驗算；第2、6階振型主要表現(xiàn)為橫向振動，頻率分別為1.99/5.31 Hz，已不在橫向振動敏感頻率范圍內(nèi)，不需要進行橫向振動的舒適度驗算。

3.2 設計工況及等效諧波荷載

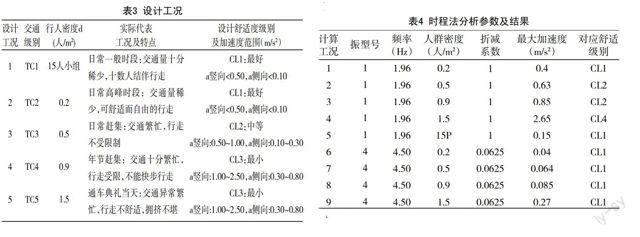
每個設計工況由一個預期的交通級別和一個選定的舒適度等級來確定，交通級別主要由橋上行人密度來表示。顯然，重現(xiàn)率高的交通級別必須滿足較高的舒適性水平，而重現(xiàn)率較低的交通級別可以采用較低的舒適度水平。根據(jù)德國指南并結合本橋的實際情況，本橋取用如下幾種具有代表性的設計工況進行驗證，見表3。

當行人密度超過1.5人/ m2時，行人基本不能行走，動力作用也會明顯減小，因此可不考慮行人密度>1.5人/ m2的工況。對于有意識的以齊步隊列行走的人群，設計不做驗證，而是在交通安全設計時以禁令標志牌的形式予以禁止。

對于n個隨機行人組成的行人流，可以用n'個完全同步的理想行人流來等效模擬。理想行人流按照下式（1）轉(zhuǎn)換為均布諧波荷載p（t）[N/m2]：

p（t）=P×cos（2πfst）×n'×？追（1）

其中：

P為單人荷載幅值，橫向取280 N，縱向取140 N，側(cè)向取35 N；

fs為步頻，假設它等于所考慮的人行橋某階固有頻率；

n'為加載面積為S時的等效行人密度：

TC1～TC3（人流密度d<1.0人/m2=：（1/ m2）（2）

TC4～TC5（人流密度d≥1.0人/m2）：（1/ m2）（3）

T為結構的阻尼比；

n為加載面積為S時的行人數(shù)，n=S×d；

？追是考慮到步頻接近基頻變化范圍臨界值的概率而引入的折減系數(shù)。

3.3 結構阻尼

結構阻尼的大小對評估行人激振是十分重要的，但想要準確的估計系統(tǒng)阻尼卻比較困難。系統(tǒng)阻尼的大小不僅與結構材料有關，而且還與振動水平有關，振幅較大時系統(tǒng)的阻尼一般也越大。

德國指南給出了不同材料類型的構造物在正常使用情況和較大振動情況下的平均阻尼比：正常使用狀態(tài)下鋼結構的阻尼比平均值為0.004，鋼筋混凝土結構的平均阻尼比為0.013。

本橋上部結構由鋼桁架及鋼筋混凝土橋面系組成，計算時阻尼比取為：小幅振動時=0.005，振幅較大時=0.02。

3.4 時程法求解最大振動加速度及舒適度驗證

時程法求解人行橋的最大振動加速度，就是將等效諧波荷載施加到結構的某一特定振型上，諧波荷載的加載方向與結構振動位移增大的方向一致，這樣每個行人的作用都是使橋梁產(chǎn)生最大加速度。

根據(jù)動力特性分析結果，本橋需就第1、4階振型對各種設計工況下的豎向振動逐一進行驗證。各計算工況參數(shù)及結果見表4。

根據(jù)上表的計算結果，計算工況4，第1階振型下當人群密度為1.5人/ m2時，人行橋振動最大加速度為2.65>2.5 m/s2（舒適度級別CL3的上限），不滿足設計舒適度要求；其余計算工況可滿足設計舒適度要求。

本橋橫向剛度較大，固有頻率在橫向振動的敏感頻率范圍之外，一般不易觸發(fā)橫向鎖定現(xiàn)象。

4 結 語

結構的阻尼比對人行橋人致振動分析結果的影響是非常顯著的，而要精確預估人行橋的阻尼比卻比較困難；另外，在進行有限元分析時，完全不計桁架上、下弦桿鋼管內(nèi)的混凝土剛度，這種有意識的削弱結構剛度的假設雖然趨于安全，但也會使有限元分析的結果與實際情況產(chǎn)生偏差。分析結果表明本橋在某些特定工況下的舒適度水平可能不滿足設計要求，因此在橋梁建成后，用實驗來測定人行橋的固有頻率、振動模態(tài)及阻尼比等動力特性是必要的。在橋梁建成后，可根據(jù)實橋?qū)嶒灉y定的動力特性來重新評估人行橋的振動響應，當確有必要時，可采取安裝TMD（調(diào)諧質(zhì)量阻尼）的方法增加結構阻尼，將人行橋振動響應控制在可接受的范圍內(nèi)。值得指出的是，本橋所采用的三角形截面鋼桁架結構由于橫向剛度相對較大，能在一定程度上減弱橫向人致振動的不利影響。

參考文獻：

[1] 陳政清，華旭剛.人行橋的振動與動力設計[M].北京：人民交通出版社，2009.

[2] CCJJ 69-95，城市人行天橋與人行地道技術規(guī)范[S].

[3] GB 50017-2003，鋼結構設計規(guī)范[S].