基于iGMAS的北斗導航衛星原子鐘性能評估

廉吉慶，張文璽，張金海，王世偉，陸 昉，翟 浩，崔敬忠，劉志棟

（蘭州空間技術物理研究所 真空技術與物理重點實驗室，蘭州 730000）

0 引言

近年來衛星導航技術發展迅速，多個國家或組織開展了全球衛星導航系統（Global Navigation Satellite System，GNSS）的建設。美國是最早建設衛星導航系統的國家，經過近半個世紀的發展，目前美國的全球定位系統（Global Positioning System，GPS）已進入GPS III階段。2020年6月我國自主建設、獨立運行的北斗三號衛星導航系統全面建設完成，并向全球提供導航定位授時服務。衛星導航系統是以時間測量為基礎的系統，導航衛星通過測量衛星與接收機之間信號發送與接收的時間，解算位置信息，因此時間系統是衛星導航系統運行的基礎。星載原子鐘作為衛星導航系統上的時間基準，是導航衛星的關鍵核心部件。根據北斗衛星導航系統星座信息[1]，北斗二號衛星搭載了高精度銣原子鐘，北斗三號搭載了性能更好的銣原子鐘和氫原子鐘，另外，北斗三號試驗星還搭載了國產銫原子鐘進行性能驗證[2-3]。本文介紹了星載原子鐘性能評估的主要參數，并利用全球連續監測評估系統（International GNSS Monitoring and Assessment System，iGMAS）提供的2019年12月到2021年2月期間鐘差數據，分析和比較目前在軌應用的北斗二號衛星銣原子鐘、北斗三號衛星銣原子鐘和氫原子鐘的各項性能，為原子鐘研制人員提供參考數據。

1 星載原子鐘的性能參數

評估星載原子鐘性能的參數有三個，分別為頻率準確度、頻率穩定度和頻率漂移率。

頻率準確度表征原子鐘輸出信號頻率與標稱頻率的吻合程度，是被測原子鐘輸出頻率偏離標稱頻率的相對數值，由式（1）表示。從式中可以看出，頻率準確度是有正負的。由于輸出頻率有短期的波動，實際頻率準確度通常取采樣時間1 h以上的數據計算平均值[4]。

頻率漂移率表征原子鐘輸出頻率隨時間變化的程度，是衡量原子鐘自主守時能力的重要參數，工程使用中通常以1天為單位對原子鐘的頻率漂移率進行測算，即天漂移。影響原子鐘頻率漂移的因素是多方面的，如控制電路元器件的老化、物理部分內部狀態的穩定程度以及外部電磁和熱環境的變化等。部分文獻認為原子鐘的頻率變化是單調的，即頻率漂移率的正負是不變的，但在實際應用中，原子鐘的頻率漂移可能呈現波動特性。基于頻率準確度數據的漂移率D估計如式（2）所示[5]：

式中：fi(τ)為ti時刻原子鐘的頻率準確度，i=1，2，3…，M；M是取樣時間為τ的總樣本數；τ為取樣時間；(τ)為頻率準確度平均值

頻率穩定度是衡量原子鐘性能的另一個重要參數，它表示了一定時間內原子鐘輸出頻率的平均波動或變化情況，通常用阿倫方差或哈達瑪方差表示。阿倫方差反映了原子鐘輸出頻率的全部變化情況，哈達瑪方差采用3點采樣計算，是針對頻率漂移率較大的原子鐘提出的方差分析方法[6]。銣原子鐘通常采用哈達瑪方差計算穩定度，以消除線性漂移的影響；氫原子鐘和銫鐘直接采用阿倫方差表示穩定度。阿倫方差和哈達瑪方差可以用鐘差或頻差數據表示[5，7-8]，由于相位是頻率的積分，因此兩種表述本質上相同。以頻差為輸入的阿倫方差σ2y(τ)和哈達瑪方差Hσ2y(τ)計算式分別如式（3）和式（4）所示：

式中：yi是第i次取樣時間τ內的平均頻率準確度。

2 北斗導航衛星原子鐘數據分析

2.1 數據來源與說明

iGMAS對用戶提供8種產品，其中鐘差數據反映了導航衛星在軌運行時間與地面標準時間的差值，可用于導航原子鐘評估，包括最終鐘差、快速鐘差、超快速鐘差和實時鐘差四種類型，其中最終鐘差精度最高。根據產品文件格式標準，iGMAS鐘差產品的內容包括版本類型、文件類型、衛星標識符、衛星系統、參考鐘數、鐘差數據等，使用時主要關注的是鐘差數據。鐘差數據文件主要包含鐘差數據類型、衛星PRN編號或接收機編號、歷元時刻、數據個數及相應的數據，如表1所列。表中AS表示該行數據為衛星數據，最后兩列數據分別為系統解算的原子鐘在軌鐘差數據和鐘差標準差[9]。

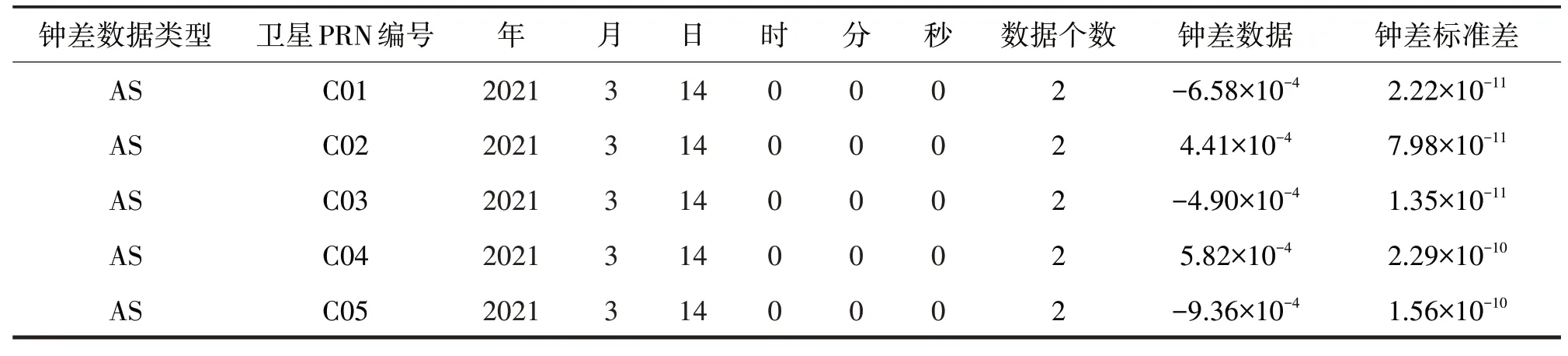
表1 鐘差數據文件Tab.1 Data format of iGMAS clock product

本文采用iGMAS提供的2019年12月至2021年2月共13個月北斗衛星的最終鐘差數據進行分析，其中2020年7月5日至2020年7月18日的最終鐘差（isc）數據缺失，計算時用同時期的快速鐘差（isr）數據代替。

北斗衛星導航系統的部分星歷如表2所列，使用的iGMAS鐘差文件中包含PRN編號為1~40的36顆衛星，包括15顆北斗二號衛星和21顆北斗三號衛星，其中北斗二號衛星與10顆北斗三號衛星使用銣原子鐘，11顆北斗三號衛星使用氫原子鐘。

表2 北斗衛星導航系統部分星歷Tab.2 Partial constellation information of BeiDou System

2.2 頻率準確度評估

本文星載原子鐘的頻率準確度以月為單位進行評估。必須說明的是，C40衛星由于發射時間較晚，準確度和漂移率評估時并未被納入，在用于分析計算的數據中，2020年7月5日至2020年7月18日的快速鐘差文件中C38和C39鐘差數據不全，對它們的準確度與漂移率評估僅利用了17天的數據。

2019年12月至2021年2月期間，北斗二號衛星銣原子鐘的頻率準確度如圖1所示，圖中的頻率準確度按月平均計算。大部分星載銣鐘準確度在±5×10-11范圍內，2020年6月后，15臺北斗二號衛星銣原子鐘的準確度絕對值均保持在1.0×10-10以內。從圖1可以看到，銣鐘在軌運行時具有較明顯的頻率漂移，并且多臺銣鐘頻率準確度出現了較大數值的跳變。星載原子鐘的頻率跳變并不意味著原子鐘的狀態異常，特別是大幅度或者有規律的頻率跳變，通常是系統操作的結果，以保證原子鐘的準確度在系統要求的范圍內。圖中C03和C04衛星的銣鐘頻率準確度跳變量最大，分別達到1.5×10-10和1.2×10-10；C08、C09、C10、C11和C16頻率準確度跳變量級相同，約為4.9×10-11；C01衛星銣鐘頻率準確度跳變量級較小，約為8.0×10-12；其余衛星的原子鐘雖然沒有明顯的頻率調整，但C02、C05和C13等衛星有小于5.0×10-12的頻率臺階或變化。

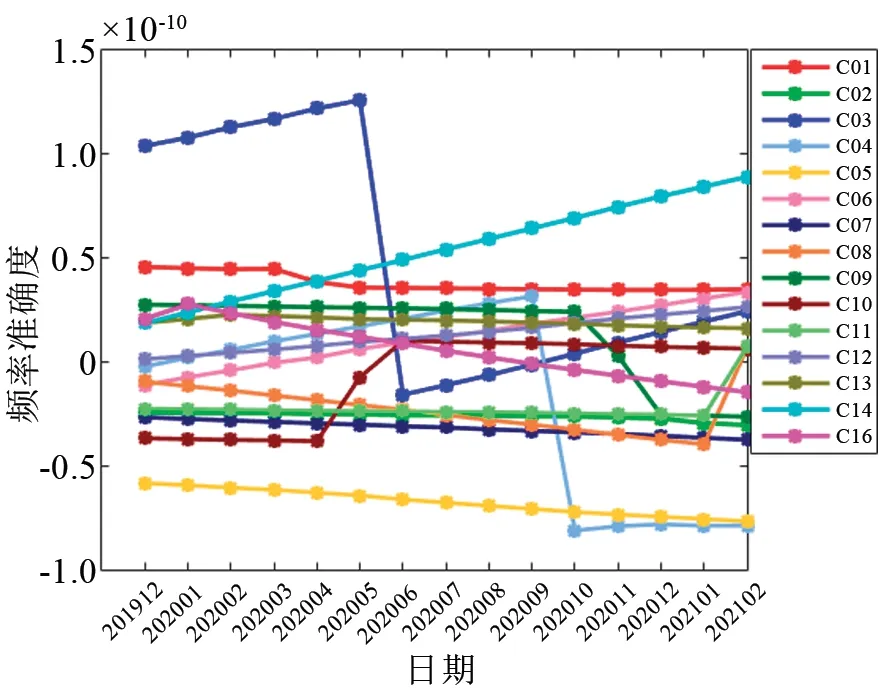
圖1 北斗二號衛星銣原子鐘準確度Fig.1 Frequency accuracy of BDS-2 RAFS

2019年12月至2021年2月期間，北斗三號衛星銣原子鐘的頻率準確度如圖2所示，準確度均在±7×10-11以內，5臺北斗三號衛星銣原子鐘的準確度保持在2×10-11以內，另外5臺的準確度在2020年8月后也保持在±2×10-11以內。總體來看，北斗三號衛星銣原子鐘的頻率準確度比北斗二號衛星銣鐘的更高。

圖2 北斗三號衛星銣原子鐘準確度Fig.2 Frequency accuracy of BDS-3 RAFS

對比圖2和圖1的準確度變化曲線可以看到，同時期內北斗三號衛星銣原子鐘的頻率準確度跳變更頻繁，可能的原因包括兩個方面：（1）北斗三號銣原子鐘的準確度要求更高，增加了頻率準確度的調整次數；（2）北斗三號衛星多數為2018年以后發射，銣原子鐘運行時間較短，根據銣原子鐘輸出信號的經驗模型，銣原子鐘運行初期頻率漂移率通常較大，導致頻率準確度調整間隔較短，但隨著運行時間的增加，銣原子鐘頻率漂移率會降低并趨于穩定。

2019年12月至2021年2月期間，北斗三號衛星氫原子鐘的頻率準確度如圖3所示。2020年4月后，北斗系統氫原子鐘的準確度普遍在±2×10-11以內，且大部分氫原子鐘的準確度優于1×10-11。與銣原子鐘相比，多臺氫原子鐘的頻率準確度不變，只有C26衛星和C35衛星搭載的氫原子鐘出現了頻率跳變，量級分別約為2×10-11和5.9×10-11。

圖3 北斗三號衛星氫原子鐘準確度Fig.3 Frequency accuracy of BDS-3 PHM

2.3 頻率漂移率評估

將鐘差數據轉換為頻差數據后，以月為單位進行天漂移率的計算，若當月出現頻率跳動的情況，分別計算頻率跳動前后的天漂移率，并按照所占時間比例加權。

圖4為北斗二號衛星銣原子鐘頻率漂移率的統計情況，C01、C02、C07、C09、C10、C11和C13衛星的銣原子鐘天漂移率絕對值均小于5×10-14，C05和C12衛星銣鐘的天漂移率絕對值在5×10-14左右，其余衛星銣鐘的天漂移率絕對值在5×10-14~2×10-13范圍內，其中C04和C16衛星銣鐘的天漂移率在2020年初較大，絕對值為1.5×10-13左右，但隨著時間的推移，這兩臺銣鐘的天漂移率呈明顯的下降趨勢，于2021年2月分別達到-4×10-14和-9×10-14左右。

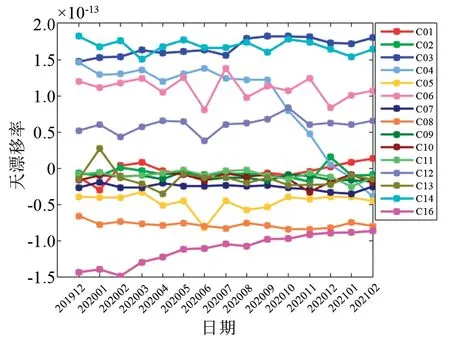
圖4 北斗二號衛星銣原子鐘頻率漂移率Fig.4 Frequency drift of BDS-2 RAFS

2019年12月至2021年2月期間，北斗三號衛星銣原子鐘輸出頻率的天漂移率如圖5所示，其中C19衛星銣鐘的漂移率很小，達到10-15量級，其余銣原子鐘的天漂移率大多在10-13量級，但這些銣原子鐘的天漂移率明顯呈減小趨勢，到2021年2月時已有5臺銣原子鐘的天漂移率進入10-14量級，這與GPS銣鐘天漂移率變化的經典模型趨勢一致[10]。

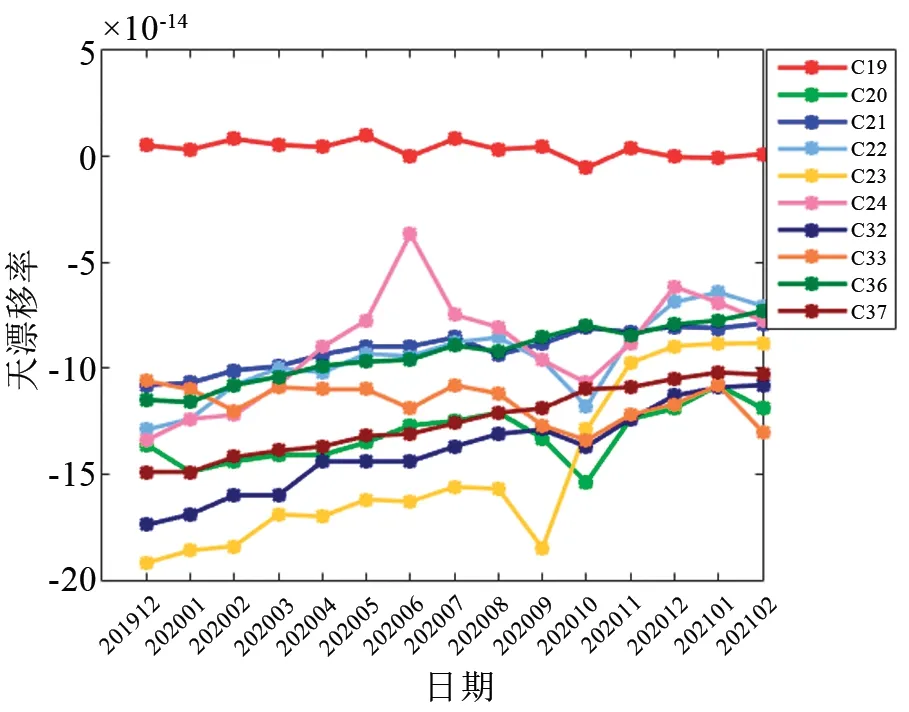
圖5 北斗三號衛星銣原子鐘頻率漂移率Fig.5 Frequency drift of BDS-3 RAFS

圖6為北斗三號衛星氫原子鐘天漂移率的計算統計情況。

圖6 北斗三號衛星氫原子鐘天漂移率Fig.6 Frequency drift of BDS-3 PHM

由圖6可以看出，所有氫原子鐘的天漂移率絕對值均達到10-15量級，且大部分時間能夠達到5×10-15以內，多臺氫原子鐘的天漂移率甚至達到10-16量級。另外，雖然氫原子鐘的漂移率仍有波動，但是多數氫原子鐘的天漂移率波動趨勢比較一致，如2020年1月、2020年6月 和2020年10月 多臺氫原子鐘出現了天漂移率負向增加的情況，可能與其他原因引入的噪聲有關。對比能夠看出，北斗系統氫原子鐘的天漂移率明顯小于銣原子鐘。

2.4 頻率穩定度評估

根據2.2節對原子鐘頻率準確度的分析，導航原子鐘的輸出頻率存在跳變和波動，并且無法根據鐘差數據直接判斷異常波動是來自于原子鐘自身、地面控制段的控制命令還是鐘差測量系統。為了更好地評估原子鐘的頻率穩定度，本文選取連續100天無異常波動和頻率跳動的數據進行穩定度計算，其中銣原子鐘采用哈達瑪方差計算，氫原子鐘采用阿倫方差計算。由于iGMAS鐘差數據的時間間隔為300 s，穩定度評估從300 s開始。

北斗二號衛星銣原子鐘穩定度趨勢如圖7所示，9 600 s以前穩定度曲線的斜率整體為τ-1/2，即輸出信號噪聲以銣原子鐘的調頻白噪聲為主。C06衛星銣原子鐘的穩定度在10 000 s以后開始變差，天穩定度約1×10-13，主要原因是該星原子鐘的準確度在評估時間內存在一定波動，其余銣原子鐘的穩定度趨勢基本一致，300 s的穩定度普遍在1×10-13~5×10-13范圍內，10 000 s穩定度在1×10-13~5×10-13范圍內，天穩定度在1×10-14~5×10-14范圍內。

圖7 北斗二號衛星銣原子鐘穩定度Fig.7 Frequency stability of BDS-2 RAFS

北斗三號衛星銣原子鐘的頻率穩定度如圖8所示。10臺銣原子鐘的穩定度一致性較好，4 800 s之前的穩定度曲線斜率整體為τ-1/2，3 00 s穩定度優于2×10-13，其中C23衛星銣鐘的300 s穩定度最好，達到1×10-13，所有北斗三號衛星銣原子鐘10 000 s左右的穩定度均優于4×10-14，天穩定度均優于3×10-14。

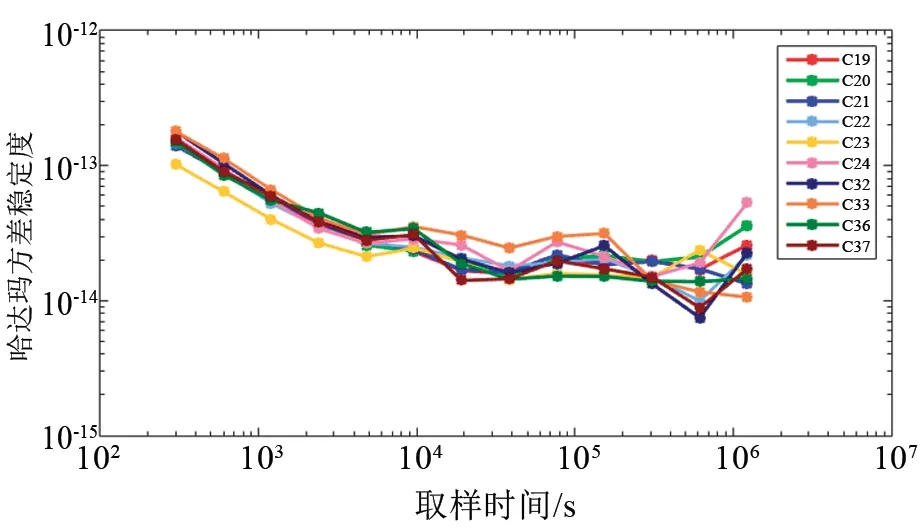
圖8 北斗三號衛星銣原子鐘頻率穩定度Fig.8 Frequency stability of BDS-3 RAFS

北斗三號衛星氫原子鐘的穩定度如圖9所示，5 000 s之前的穩定度曲線斜率整體為τ-1/2，300 s穩定度優于2×10-13，其中C34和C40衛星氫原子鐘的300 s穩定度最好，優于1×10-13，北斗衛星氫原子鐘的指標一致性較好，且長期穩定性能優異，10 000 s左右的穩定度為1×10-14~3×10-14，所有氫原子鐘的天穩定度均優于3×10-14，并且隨著時間常數的增加，仍呈下降趨勢。

圖9 北斗三號衛星氫原子鐘頻率穩定度Fig.9 Frequency stability of BDS-3 PHM

北斗二號衛星銣原子鐘、北斗三號衛星銣原子鐘和氫原子鐘的穩定度分別平均后的數據如圖10所示，計算時剔除了北斗二號衛星銣原子鐘存在波動的C06，北斗三號衛星氫原子鐘的C25、C38和C39。對比可見，北斗三號衛星銣原子鐘和氫原子鐘的穩定度明顯高于北斗二號衛星銣原子鐘的穩定度。取樣時間在1天之內時，北斗三號衛星銣原子鐘的穩定度與氫原子鐘的穩定度指標相近，隨著取樣時間的增加，氫原子鐘的穩定度優于銣原子鐘的穩定度，達到10-15量級。

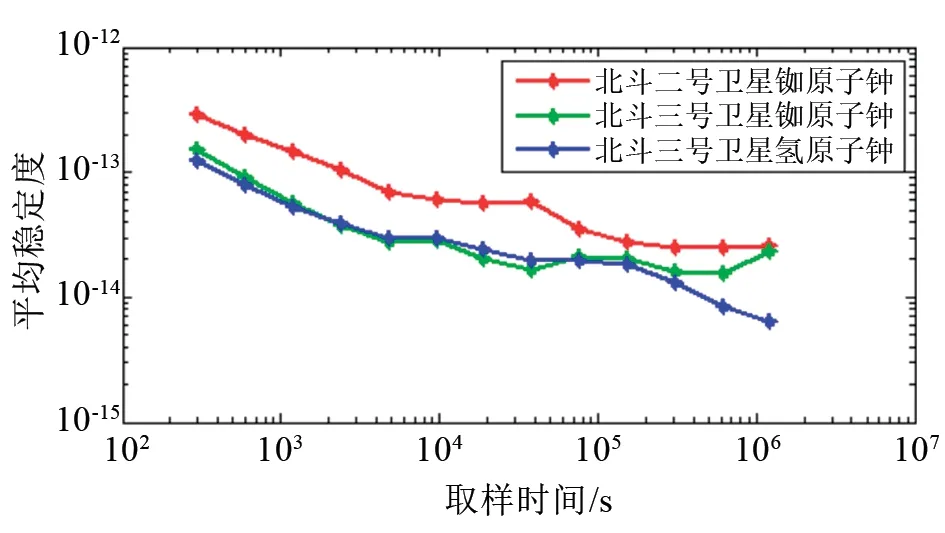
圖10 北斗導航衛星原子鐘平均穩定度Fig.10 Frequency stability comparison of BDS atomic frequency standard

3 總結

北斗衛星導航系統的原子鐘包括銣原子鐘和氫原子鐘，其中北斗二號衛星使用銣原子鐘，北斗三號衛星使用性能更好的銣原子鐘和氫原子鐘，本文利用iGMAS提供的2019年12月至2021年2月的最終鐘差數據，對北斗導航衛星原子鐘的性能進行了評估，結果表明，北斗三號衛星使用的原子鐘比北斗二號的性能明顯提升，其中氫原子鐘的長期性能更好，10天穩定度和天漂移率普遍達到10-15量級。星載原子鐘性能的提升能夠有效改善衛星導航定位精度。未來隨著更高精度原子鐘的開發應用，衛星導航定位的精度將會進一步提升。需要說明的是，本文對iGMAS鐘差數據轉換得到的原子鐘準確度數據僅進行了必要的粗差剔除并未做進一步的優化處理，考慮到鐘差數據本身包含評估噪聲，因此作者認為，北斗原子鐘實際穩定度性能優于本文評估的結果。

致謝

感謝iGMAS提供的衛星鐘差產品。