基于三維熱變形原理的轉站誤差補償方法

俞慈君,楊寶旒,金漲軍,李江雄,柯映林,李明飛,方 強

（1.浙江大學機械工程學系,浙江杭州310027；2.中航工業陜西飛機工業（集團）有限公司,陜西漢中723313）

基于三維熱變形原理的轉站誤差補償方法

俞慈君1,楊寶旒1,金漲軍1,李江雄1,柯映林1,李明飛2,方 強1

（1.浙江大學機械工程學系,浙江杭州310027；2.中航工業陜西飛機工業（集團）有限公司,陜西漢中723313）

為了提高飛機裝配大尺寸測量精度,提出針對公共觀測（ERS）點熱變形引起的轉站誤差的補償方法.該方法基于物體的熱變形理論建立工裝各向異性的三維熱變形模型,對ERS點的實際位置進行修正,構建修正后的ERS點位置和理論位置之間的最小加權距離誤差函數作為優化模型.轉站過程中采用3σ準則對參與轉站的ERS點進行篩選,剔除超差的異常點.采用單純形法求解該優化模型,獲得滿足3σ準則的轉站點組和最優轉站參數.工程算例表明,采用該方法可以有效地剔除異常點并減少轉站誤差,提高了裝配系統的測量精度.

激光跟蹤儀；轉站誤差；三維熱變形；3σ準則；單純形法

在現代航空工業中,激光跟蹤儀具有精度高、測量范圍大、操作簡單、便于移動等優點,在航空制造和裝配過程中得到了廣泛的應用［1-2］.在裝配測量的過程中,待測點可能超出激光跟蹤儀的測量范圍,須移動跟蹤儀從不同位置和角度去測量待測點坐標.通過“轉站”的方式建立不同位置下的跟蹤儀測量坐標系和飛機裝配坐標系的關系.“轉站”是用一組空間固定分布的公共觀測點（enhanced reference system,ERS）在2個坐標系下的坐標值進行匹配,獲得測量坐標系在裝配坐標系下的位姿關系.轉站誤差越小,則轉站越精確.

布置在工裝設備或地面上的ERS點易受溫度、震動、濕度等環境因素的影響,使位置發生偏移,造成轉站誤差.其中溫度變化引起的ERS點位置偏移（熱變形）尤為顯著,極大地降低了跟蹤儀的轉站精度.目前主要采用2種方法減少溫度變化引起的工裝熱變形［3］.1）采用車間內的恒溫技術.該方法在大部件裝配中成本高昂且技術難度大,以20 m的裝配空間為例,即使控制溫度波動在5℃范圍內,取鑄鐵線膨脹系數為10－6／℃,變形量仍達1 mm.2）根據溫度變化引起的物體熱脹冷縮具有的規律性,建立熱變形誤差模型,采用誤差補償技術來減小熱變形誤差的影響.該方法只需要相應精度的溫度測量系統和熱變形誤差模型,因此更加經濟實用.

提高轉站匹配算法精度通過以下兩方面著手解決：1）研究不同的匹配算法：Wang等［4］針對每一個參與匹配的測量點的測量精度不同的問題,提出基于動態加權的匹配方法的求解方法,一定程度上減少了激光跟蹤儀測量誤差引起的轉站誤差.俞慈君等［5］提出帶工程約束的點匹配方法,在實際工程約束下獲得最佳的匹配精度,該算法對誤差作了符合約束要求的分配,但不能減小誤差.2）研究匹配點的熱變形和補償方法：Horn等［6］提出一種基于測量點組相似性加入了比例系數s的匹配補償方法,該方法在小范圍內的固定檢測點發生規律性偏移的圖像匹配領域得到較好應用.Horn法也可以部分補償由于熱變形引起的轉站誤差,但實際每個點的熱變形是各向異性的,該方法過于理想化.ERS點熱變形造成的激光跟蹤儀轉站誤差問題,目前尚沒有文獻對此進行專門研究.

本文首先介紹激光跟蹤儀轉站的基本原理,針對ERS點熱變形引起的轉站誤差,提出基于三維熱變形原理的轉站誤差補償方法.該方法采用各向異性的三維熱變形模型對ERS點的位置進行修正,然后以修正后的ERS點位置和理論位置之間的最小加權距離誤差函數作為優化目標函數.將ERS點熱變形視作測量的系統誤差,同時考慮到ERS點可能由于撞擊、振動、聯結松動等原因造成粗大誤差,引入3σ準則對參與轉站的ERS點進行篩選,剔除超差的異常點.采用單純形法求解該非線性最優化模型,獲得滿足3σ準則的轉站點組和最優轉站參數.工程算例表明,采用本文方法有效地剔除異常點并減少轉站誤差,提高了裝配系統的測量精度.

1 激光跟蹤儀轉站

1.1 轉站原理

激光跟蹤儀“轉站”是為了獲得測量坐標系OB在裝配坐標系OA下的位置和姿態參數,然后設置參數使測量坐標系和裝配坐標系重合,如圖1所示.轉站參數用（α,β,γ,tx,ty,tz）來表示.其中（tx,ty,tz）表示激光跟蹤儀測量坐標系相對于裝配坐標系的平移量；（α,β,γ）為ZYX歐拉角［7］,表示激光跟蹤儀測量坐標系相對于裝配坐標系的旋轉變換序列.

令T＝［tx,ty,tz］T,

式中：sθ＝sinθ,cθ＝cosθ,T為平移矩陣,R為旋轉矩陣.

裝配坐標系下的實測坐標p′Ai和轉站點誤差ei為

采用奇異值分解法（singular value decomposition,SVD）求解式（1）.該方法對誤差不作任何補償,本文只簡單介紹和應用其解法,在文獻［8］中有嚴格證明.

對于第i個ERS點,裝配坐標系下的理論坐標和測量坐標系下的實測坐標分別為pAi和pBi,對于所有n個測量點,轉站計算的最小二乘表達式如下：

圖1 激光跟蹤儀轉站示意圖Fig.1 Coordinate transformation in station movement of laser tracker

式（4）簡化為

求解Σ2的最小值是求解下式的最大值：

對矩陣H進行SVD分解,使得

式中：D為一個對角陣,U和V為正交單位矩陣.

旋轉矩陣R為

平移矩陣T為

1.2 帶比例系數的Horn法轉站原理

為了減少匹配誤差,Horn等［6］在研究圖像處理過程中的點匹配問題時,加入了表示2個點組之間的相似程度的比例系數s.

轉站計算的最小二乘表達式（1）轉變成如下形式：

同理,式（6）轉化為

將式（12）改寫為幾何對稱式（13）的形式,兩者是等價的,在文獻［7］中有詳細的證明.

展開式（13）可得

令

可得

1.3 現有方法的不足

Horn提出的基于測量點組相似性的匹配補償方法,在小范圍內的固定檢測點圖像匹配領域取得了較好的效果.對于航空裝配現場的三維大尺寸測量的跟蹤儀轉站來說,Horn的方法存在如下不足.

1）ERS點一般固定在大型工裝、型架上.由于材料、形狀結構、尺寸和組裝方法的不同,工裝、型架在主要尺寸（長寬高）方向上會表現出各向異性的熱膨脹特性［9］.因此,Horn法中使用比例系數s,即假定各向同性變形是不合理的.

2）Horn補償模型只對平移參數進行了修正,認為ERS點的偏移（相對于中心點的縮放）是完全理想化的,不會改變轉站的旋轉參數.事實上,由于ERS點的偏移是非對稱的,旋轉參數會發生細微的變化.

3）SVD法和Horn法都沒有將溫度變化引起的熱變形看作系統誤差,也沒有對ERS點的異常變形情況進行分析.

針對以上不足,本文提出一種對轉站熱變形誤差進行補償的解決方法.

2 熱變形模型

溫度變化容易引起零件或部件幾何形體的變化,使得實際參數和幾何形體偏離設計的理想狀態,這種由溫度變化引起實際參數與理想參數之差為熱變形誤差.傳統物體熱變形公式是線性公式,它包含幾何尺寸、材料熱膨脹系數和實際溫度3個參數,即物體幾何尺寸的熱變形誤差是由上述3個參數確定的線性函數,傳統熱變形計算公式存在近似性.實際上零部件的各個尺寸具有相關性,任一尺寸的熱變形誤差是其他相關尺寸的函數.由于尺寸間的相互制約,熱變形后的零部件尺寸可能增加,也可能縮小,還可能保持不變［9］.

由于每次轉站的過程時間很短（＜10 min）,可以假設在該過程中環境溫度一定,且所有的ERS點與現場環境之間處于熱平衡狀態,即ERS點處于空間分布均勻的穩態溫度場中.若ERS點在標定時的溫度為T0,進行轉站測量時的溫度為T,這兩者之間可能經過了幾天甚至幾個月,則由溫度差ΔT＝T－T0引起的熱變形是導致轉站誤差的主要原因.

假設部件上某一尺寸在溫度T下的尺寸為Xi,在標準溫度T0下為Xi0,兩者的比值為si,則有

式中：si為熱變形比例系數,si不僅和材料熱膨脹系數α及溫度T有關,同時和部件所有尺寸綜合影響Xi變形的邊界條件函數Ω有關.

某ERS點在標準溫度T0下的坐標為p0＝［px0,py0,pz0］T,在溫度T下的坐標為p＝［px,py, pz］T,代入式（16）可得

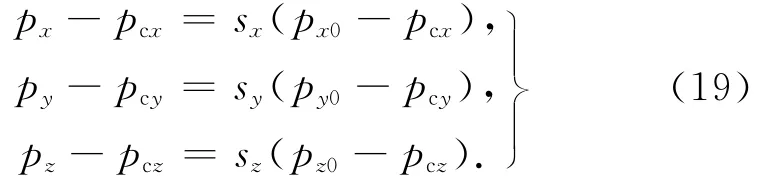
整理可得

式中：pc為部件變形的參考點,在pc點處物體尺寸的變形量為零；sx、sy和sz分別為三維方向上的熱變形比例系數.將式（20）寫成如下矩陣形式：

式中：S為熱變形比例系數對角矩陣,可以簡寫為S＝diag（sx,sy,sz）,tc為參考中心偏置矩陣,

3 轉站的熱變形誤差補償

飛機裝配工裝的結構一般具有對稱性,ERS點一般對稱布置于材料相同、結構近似的工裝上.顯然,單個ERS點在X、Y和Z方向的熱變形具有各向異性.考慮到全部參與轉站的ERS點所形成的空間整體,不同的ERS點在X、Y和Z單個方向的熱變形具有近似一致性,膨脹或者收縮.下文的熱變形系數sx、sy和sz表示全部ERS點在各方向上的一個平均熱變形系數.

3.1 熱變形誤差補償算法

根據式（21）,將式（2）修正為

式中：

此時,轉站計算的最小二乘表達式如下：

根據式（11）、（12）、（24）轉化為

式中：

于是,式（26）簡化為

由式（26）可知,當S＝diag（s,s,s）,pc＝［0,0,0］T時,與式（14）等價,即Horn法是本文方法的一個特例.

3.2 參考中心的選取

由式（23）可知,新平移矩陣T′是熱變形比例系數矩陣S、參考中心偏置矩陣tc以及平移矩陣T的函數.由式（26）可知,當ΔT＝0時,有T′＝μA－SRμB,則T′的解僅依賴于μA、μB、S和R,與參考中心pc的選擇無關.當S和R確定后,T′具有唯一解.選取參考中心的位置為原點,即pc＝［0, 0,0］T,則有tc＝0.

式（24）簡化為

3.3 補償算法求解

式（28）是一個典型的無約束非線性優化問題：形如f（v）＝minΣ2,須優化的未知參數為v＝（α, β,γ,tx,ty,tz,sx,sy,sz）,即轉站參數和熱變形比例系數.由于未知參數較多,本文采用單純形法（Nelder-Mead算法）［10］求解該優化問題.該方法屬于直接搜索法,無需計算函數的梯度,求解簡單,易得全局最優解.應用單純形法需要先確定初值v0,本文的轉站參數初值使用SVD法計算得到,取比例系數初值為（1,1,1）.得到初值v0后,可以根據單純形法對熱變形誤差補償模型進行求解.數值分析軟件MATLAB中的工具箱提供了解決最優化問題的現成函數,其中fminsearch函數［11］的計算原理是Nelder-Mead算法,本文對式（28）直接調用該函數進行求解.函數的輸入為式（28）的函數表達式和v0,輸出為最優化目標參數v*.

4 異常點剔除的3σ準則

裝配現場ERS點的一般布置比較穩定,相對于原來位置的偏移較小,但會由于一些原因出現一些偏移較大的異常點：1）聯結松動、物體撞擊、人為移動等造成被測點漂移；2）不規范的設備操作或設備異常造成被測點測量值失真.這些異常點屬于壞點,若參與轉站計算則會增大轉站誤差,并且影響轉站參數的準確性,故須在轉站計算時予以判斷和剔除.

本文中異常點的剔除方法采用拉伊達（Pau Ta）準則,簡稱3σ準則［12］.將超過3σ的數據點進行剔除,該方法犯“棄真”錯誤的概率僅為0.27%.

若

則將第i個ERS點剔除.

式中：

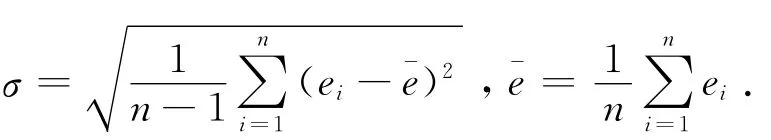
在實際應用中,應盡量使n≥10,否則不能應用該準則.

為了實現智能剔除,對每個ERS點添加權重系數ωi,初值為1.應用3σ準則,當第i個ERS點被判定為異常點時,取ωi＝0實現剔除.

式（28）轉變為

對于應用3σ準則檢查多個可疑數據時,可疑數據應逐一檢查,不能同時檢查多個數據.這是因為不同數據的可疑程度是不一致的,應按照與偏差的大小順序來檢驗.首先檢驗偏差最大的數,若這個數不被剔除,則所有的其他數都不應被剔除.

具體步驟如下.

1）先令所有權重系數的初值ωi＝1,即所有ERS點參與轉站計算,由式（30）獲得一組轉站參數后,通過式（29）計算xi、和σ.

2）若xi＞3σ,則wi＝0,n＝n－1轉步驟3）；若xi≤3σ,則結束判斷轉步驟4）.

3）重新計算式（30）,獲得新的一組轉站參數,并通過式（29）計算xi、和σ,轉步驟2）.

4）輸出剔除異常點后的最優轉站參數v*.

如圖2所示為異常點判斷剔除的流程圖.

圖2 異常點剔除流程圖Fig.2 Process of outliers rejection

5 實驗和數據分析

5.1 實驗內容

為了驗證本文方法的有效性,以某型飛機部裝現場的轉站數據為樣本,采用提到的3種方法分別進行轉站計算,比較異常點是否剔除對轉站誤差的影響.

圖3 ERS點布置示意圖Fig.3 Layout of ERS points

如圖3所示為某飛機裝配車間現場共20個ERS點空間布置示意圖.現場所用跟蹤儀型號為Leica AT901絕對激光跟蹤儀,設備的標定精度為±15μm＋6μm／m,實際測量誤差比標定的誤差更小.一般ERS測量誤差不會超過0.05 mm,而轉站誤差一般約為0.5 mm,故測量誤差屬于微小誤差,予以忽略.

如表1所示為在12℃下,標定ERS點的理論坐標和在20℃下,ERS點在測量坐標系下的實測坐標.

表1 ERS點的理論值和實測值Tab.1 Nominal and measured coordinates of ERS points

5.2 數據分析和結論

在本次實驗中,轉站精度采用轉站平均誤差和轉站最大誤差來表示,計算公式如下.

最大誤差為emax＝max｛ei｜i＝1,2,…,n｝.

應用本文的3種方法,不剔除異常點,得到圖4（a）所示的轉站誤差分布；剔除異常點,得到圖4（b）所示的轉站誤差分布.如表2所示為2種情況下的轉站平均誤差和轉站最大誤差.

當剔除異常點后,所有ERS點在XYZ向應用3種方法獲得的轉站誤差對比如圖5所示,對應的在XYZ向的轉站平均誤差和轉站最大誤差如表3所示.通過計算可得Horn法比例系數為：s＝1.000 056；本文方法的熱變形系數為：sx＝1.000 032,sy＝1.000 069,sz＝0.999 942.

表2 異常點對轉站平均誤差和轉站最大誤差影響Tab.2 Ef f ec t s o f mean er r or and maximum er r or due to ou t l ier s mm

表3 X、Y和Z向的轉站平均誤差和最大誤差Tab.3 Mean error and maximum error in X,Y,and Z directions

對數據進行分析可得如下結論.

1）由圖4（a）可知,當不剔除異常點時,ERS點L5和R5處的誤差呈現明顯異常尖點.圖4（b）表明,當應用3σ準則時,有效剔除L5和R5,使其不再參與轉站計算,轉站誤差隨之合理分布,誤差波動減小.

2）表2的結果顯示,相比于不剔除異常點,剔除異常點后,3種方法的轉站平均誤差分別減小了9.5%、29.7%、52.4%；轉站最大誤差分別減小了50.0%、65.4%、79.7%.本文方法的轉站平均誤差和最大誤差相比不作補償的SVD法減小了82.9%和71.2%,相比Horn法減小了48.1%和46.1%,直接證明了本文方法補償ERS點熱變形的有效性.

圖4 異常點對轉站誤差的影響Fig.4 Effects of registration error due to outliers

3）圖5（a）、（b）的結果顯示,在X向和Y向中,采用本文方法顯著降低了轉站誤差,并且誤差更貼近零軸分布.圖5（c）中,Z向表示豎直方向的熱變形,由于本身的變形量相較X向和Y向很小,對轉站誤差的影響較小.另外,由于工裝結構的原因,Z向變形的規律性較弱,優化效果很有限,還需進一步的研究.表3的結果表明,本文方法與SVD法和Horn法相比較,3個方向的轉站平均誤差和轉站最大誤差均有不同程度的降低.

4）采用本文方法得到的熱變形比例系數表明,雖然溫度升高,但由于工裝結構的原因,在X和Y向發生膨脹變形,在Z向發生收縮變形.Horn的單一系數法具有局限性,實際上工裝熱變形受本身結構的影響,呈現各向異性.

6 結 語

本文基于物體的熱變形理論,建立ERS點各向異性的三維熱變形補償模型,減小了熱變形引起的系統誤差影響.引入3σ準則對參與轉站的ERS點進行篩選,消除粗大誤差的影響.工程實例表明,采用本文方法有效地剔除了異常點并減小了轉站誤差,提高了裝配系統的測量精度.

圖5 3種方法的轉站誤差對比Fig.5 Comparison of three methods registration error

［1］韓清華,鄭保,郭宏利,等.采用激光跟蹤儀測量飛機外形［J］.航空計測技術,2004,24（1）：15- 17.

HAN Qing-hua,ZHENG Bao,GUO Hong-li,et al.Measurement of aircraft outline by using laser tracker equipment［J］.Aviation Metrology and Measurement Technology,2004,24（1）：15- 17.

［2］蔡聞峰,周惠群,何穎.激光跟蹤儀在無人飛機總裝中的應用［J］.工具技術,2006,40（8）：77- 80.

CAI Wen-feng,ZHOU Hui-qun,HE Ying.Study and application for UAV assemble by laser tracker［J］.Tool Engineering,2006,40（8）：77- 80.

［3］費業泰.機械溫度變形理論及應用［M］.北京：國防工業出版社,2009.

［4］WANG Zheng-yan,JEPSON Allan.A new closed-form solution for absolute orientation［C］//Proceedings of CVPR’94.Seattle：IEEE,1994：129- 134.

［5］俞慈君,李江雄,余鋒杰,等.帶工程約束的點匹配算法［J］.機械工程學報,2010,46（5）：183- 190.

YU Ci-jun,LI Jiang-xiong,YU Feng-jie,et al.3D points registration algorithm with engineering constraints［J］.Journal of Mechanical Engineering,2010,46（5）：183- 190.

［6］HORN B K P,HILDEN H,NEGAHDARIPOUR S.Closed-form solution of absolute orientation using orthonormal matrices［J］.Journal of the Optical Society of America A,1988,5：1127- 1135.

［7］蔡自興.機器人學［M］.北京：清華大學出版社,2000.

［8］ARUN K S,HUANG T S,BLOSTEIN S D.Leastsquares fitting of two 3-D point sets［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence,1987, 9（5）：698- 700.

［9］費業泰,羅哉.精密技術中熱變形誤差影響的基本問題［J］.納米技術與精密工程,2003,46（5）：183- 190.

FEI Ye-tai,LUO Zai.Basic problems about thermal deformation error in precision technology［J］.Nanotechnology and Precision Engineering,2003,46（5）：183-190.

［10］姚恩瑜,何勇,陳仕平.數學規劃與組合優化［M］.杭州：浙江大學出版社,2001.

［11］林雪松.MATLAB 7.0應用集錦［M］.北京：機械工業出版社,2006.

［12］王巖.試驗設計與MATLAB數據分析［M］.北京：清華大學出版社,2012.

Compensation method for registration error of laser tracker based on three-dimensional anisotropic thermal-deformation theory

YU Ci-jun1,YANG Bao-liu1,JIN Zhang-jun1,LI Jiang-xiong1, KE Ying-lin1,LI Ming-fei2,FANG Qiang1
（1.Department of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China；2.AVIC Shanxi Aircraft Industry Group Limited Company,Hangzhou 723313,China）

A compensation method was proposed to reduce the registration error rising from the movement of ERS points（points of enhanced reference system）due to the alteration of temperature in order to improve measurement accuracy in the aircraft assembly process.An anisotropic three-dimensional thermaldeformation model was constructed to correct the coordinates of the ERS points based on the thermal-deformation theory.Then an objective function for least-squares optimization,which is a weighted distance error between the corrected coordinates and the nominal coordinates,was constructed.The 3σcriterion was applied to filter the ERS points,and some outliers were rejected.The Nelder-Mead method was used to acquire the points by satisfying the 3σcriterion and the optimal registration parameters.The engineering example showed that outliers were effectively excluded,the registration error was reduced and the accuracy of the measurement assembly system was improved by using this new method.

laser tracker；registration error；three-dimensional thermal-deformation；3σcriterion；Nelder-Mead method

10.3785／j.issn.1008-973X.2015.07.002

V 262

A

1008- 973X（2015）07- 1208- 07

2014- 06- 01. 浙江大學學報(工學版)網址：www.journals.zju.edu.cn／eng

國家自然科學基金資助項目（51275463）；中央高校基本科研業務費專項資金資助項目（2015FZA4002）.

俞慈君（1981－）,男,助理研究員,從事飛機數字化裝配測量技術的研究.ORCID：0000-0001-9380-9009.

E-mail：yuppy＠zju.edu.cn

方強,男,副教授.ORCID：0000-0003-3947-0416.E-mail：Fangqiang＠zju.edu.cn