移動保供電電源儲能電池優化配置

杜兆斌　陳　曾　管　霖　席云華　黃　平　黃耀鵬

（1. 華南理工大學電力學院　廣州　510640

2. 廣州電力設計院　廣州　510620）

移動保供電電源儲能電池優化配置

杜兆斌1陳曾1管霖1席云華2黃平1黃耀鵬1

（1. 華南理工大學電力學院廣州510640

2. 廣州電力設計院廣州510620）

高質量的供電要求促使保供電業務不斷發展，而靈活可靠的保供電電源技術則是滿足實際需求的關鍵。在綜合考慮經濟性、并聯設計的安全可靠性以及移動性（重量要求）等因素的條件下，提出了一種移動保供電電源UPS電池優化配置模型，模型考慮了電池容量的離散特性及最大容量限制，并允許UPS電池的逆變（直流）電壓作為一個可變參數調整；采用含維變異算子的云自適應粒子群算法求解得到UPS電池的最優配置方案。算例證明了所提出的模型和算法的可行性和有效性。

保供電移動電源蓄電池多目標粒子群算法維變異算子云理論

0　引言

近年來，隨著對供電服務質量要求的不斷提高，有著保供電需求的用戶也越來越多。電力服務運營商可根據不同用戶的保供電時間、供電可靠性以及電能質量的要求提出具體適用的保供電方案[1,2]。在實際中，要實現保供電服務，除了嚴密的組織和管理外，保供電電源的配置模式、電源組合設計及運行技術也是關鍵條件[3,4]。

對于供電中斷時間必須控制在幾十ms以內的用戶，往往采用在線式不間斷電源（Uninterrupted Power Supply, UPS）作為保供電電源[5]。對于這類UPS，其蓄能元件除常用的鉛酸蓄電池外［6，7］，磁飛輪和超級電容也逐漸見諸報道[8-14]，尤其是面對短時大電流供電需求。磁懸浮飛輪儲能系統雖然具有體積較小、功率密度較大的優點，但在使用時，每換一個使用場地，都需要較長的時間來對磁懸浮飛輪做平衡調節，因此難以滿足緊急情況下快速保障電力供應的要求。此外，面對10min級保供電要求，磁飛輪和超級電容兩者都失去了技術優勢。

閥控鉛酸蓄電池（Valve Kegulated Lead Batteny, VRLA）密封性好、免維護、價格相對便宜且應用廣泛，但重量比能量較低，約30～100W·h/kg[12]。用于移動式UPS保供電電源時，供電容量（持續性）和便攜性存在難以協調的矛盾。相比VRLA，新興的鋰電池具有重量比能量高、電流放電率大和壽命長等優點[15,16]。如果鋰電池制造工藝發展，價格進一步下降，移動式鋰電池UPS將有廣闊應用前景。

對于大型城市的保供電任務，往往存在保供電電源的移動性需求[9]。但由于交通條件、保供電場所空間限制和車輛承重要求等困難難以克服，針對此類需求的車載UPS電源方案，其電池配置需要綜合考慮電池容量、并聯支路數和電池重量等多種因素。由于電池的容量是離散的而且有限，目前的配置方案中，大多是根據經驗，通過人工查表的方式定性地分析各參數對電池配置方案的影響[9]，無法做到科學準確的綜合分析。這種做法往往很難使配置的UPS電池達到最優或者較優的性能。

本文的研究本質是一個多目標優化問題。由于目標之間的不可比較和矛盾等原因，通常不存在對所有目標都最優的解。因此，多目標問題通常存在一個解的集合，其中的解不能簡單地相互比較優劣［17］。將粒子群優化（Particle Swarm Optimization, PSO）算法應用于多目標優化問題是近年研究熱點。該算法搜索的多方向性和全局性特點，使得帶有潛在解的種群得以持續改進并向Pareto最優解集逼近。其中一個關鍵問題是，如何根據多個目標來確定個體適應值，稱為適應值分配機制[18]。

本文首先提出了一種車載移動式UPS電池優化配置模型，包括UPS電池的價格、并聯支路數和電池重量組成的綜合目標函數，并考慮UPS逆變電壓為可控變量以及UPS整體參數的約束條件［19］；然后提出含維變異算子的云自適應粒子群算法（Cloud Adaptive Particle Swarm Optimization Dimension Mutation Operator, CAPSO-DMO）對優化模型求解[20-24]；最后通過權重因子的不同取值獲得電池配置方案的最優解集，通過比較分析可以較容易地找到工程決策過程中優先選擇的解，使方案具有代表性。

在傳統PSO算法的基礎上，本文將云理論[25]和變異機制[26]引入到基本的PSO算法中，提出的CAPSO-DMO可以平衡算法的全局搜索能力和局部搜索能力，提高種群多樣性，而且具有跳出局部最優解的優點，大大提高了算法的全局尋優能力。

1　UPS電池配置優化模型

以蓄電池作為儲能元件的車載移動式保供電電源設計，在滿足保供電能量和功率等要求下，當蓄電池的并聯組數過多，并聯電路間的環流就會越明顯，消耗在蓄電池內阻上的能量也就越多。此外，蓄電池的個數過多時，這不僅涉及到重量和體積限制，還因為蓄電池的數量一旦過多，蓄電池之間的一致性的控制難度就增加，而且弱項蓄電池（Weak Battery, WB）存在的可能性也大大增加[27]。針對以上問題，本文根據經濟性、安全可靠性和電池總重量等方面，構造出UPS電池配置優化模型。

UPS的電池優化配置方案描述為

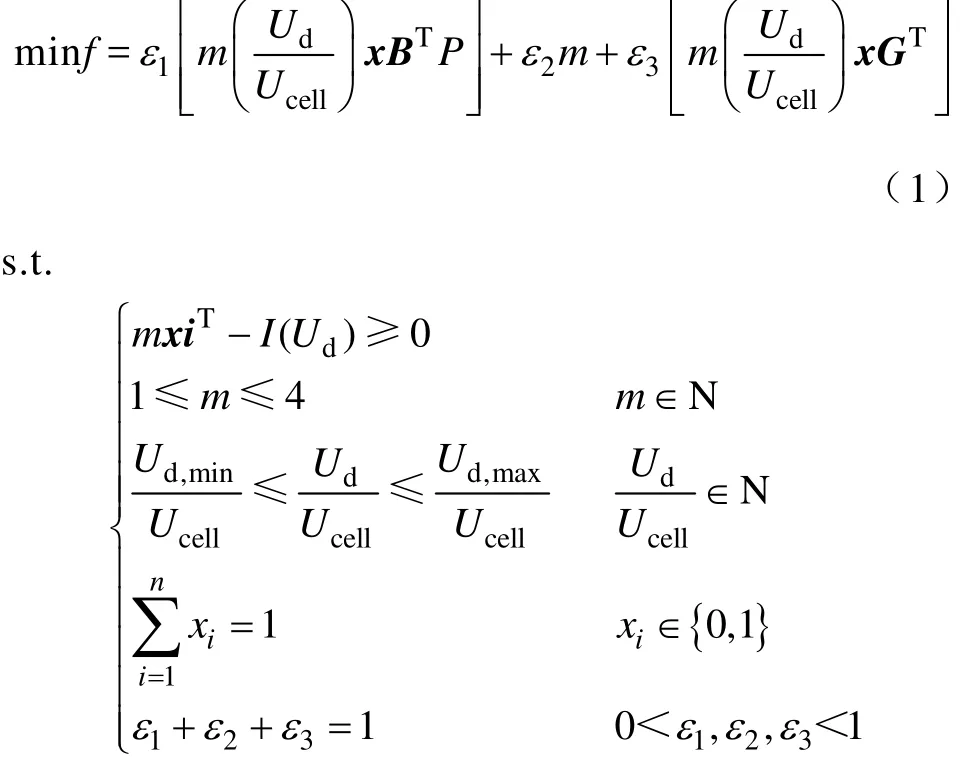
上述模型包含三個子目標，ε1、ε2和ε3為三個子目標的權重因子，本文通過線性加權的方法將多目標優化問題轉化為單目標優化問題，然后采用單目標優化算法來求解，并進一步通過不斷變換權重系數來尋找最優解[17,22]；m為電池組的并聯支路數；Ud為UPS的直流電壓；Ucell為單個蓄電池的額定電壓；對同一品牌不同型號的蓄電池（設有n個），設置一組索引變量x=（x1, x2,…,xn），如方案配置第k號電池，則xk=1，其余索引變量均為0，即每個電池配置方案由相同型號的電池組成；B= (b1, b2,…,bn)為不同型號的電池容量序列，單位為A·h；P為電池價格，單位為元/(A·h)；G=(g1, g2,…,gn)為不同型號電池重量集合；N為自然數。

在實際計算中，對上述三個子目標均作規格化處理，以解決多目標之間不同量綱的問題。每個子目標分別將電池規格表中提供的各個參數最大取值代入子目標表達式中得到基準值，然后每個子目標分別規格化。權重因子ε1、ε2和ε3可根據用戶對電源實際性能的不同偏好取值，給決策者提供了更多選擇。本文側重于保供電方案的移動性，故相應地加大ε3的取值。

關于模型中的約束條件解釋如下：

（1）第一個約束條件要求UPS電池配置方案必須滿足最大負荷需求。在一定的放電時間、溫度和臨界放電電壓條件下，不同型號的蓄電池的放電電流集合為i=(i1, i2,…,in)，單位為A。mxiT為蓄電池組提供的放電電流。根據放電電流法[6,7]，UPS負載的最大電流需求為

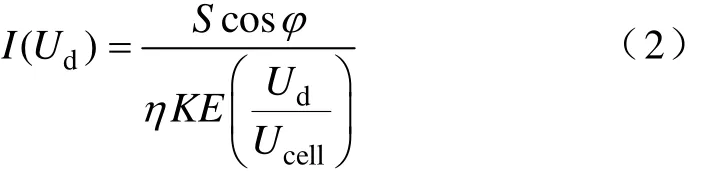
式中，S為UPS輸出額定容量；cosφ為UPS輸出功率因數；η為UPS輸出逆變器效率；K為蓄電池放電效率；E為單個蓄電池臨界放電電壓。

（2）對于電池的配置組合，在滿足UPS直流電壓Ud的要求下，可以采用多路電池組并聯的方式為較大負荷供電。但考慮到電池組并聯支路數的增加會導致系統供電安全性和可靠性的下降，建議取1≤m≤4。

（3）設UPS采用三相橋式全波12脈沖整流技術[19]，若輸入的線電壓有效值為380V，Ud最高可達618V，即380V=Ud,min≤Ud≤Ud,max=618V。如果用多個蓄電池串聯的方式為UPS提供直流電源，則Ud的值為單個蓄電池額定電壓Ucell的整數倍。

x、m和Ud為優化問題的三個控制變量。在UPS設計階段，在逆變（直流）電壓可調的情況下，其值將對按前面原則配置的電池方案產生重要影響：如果直流電壓高，需用更多的單體電池組成一條支路供電，也就意味著當其他條件相同時，一條支路能提供更多的能量，這樣的安排有可能減少所需的并聯支路數目。

2　含維變異算子的云自適應粒子群算法

對于上節提出的非線性整數規劃模型，本文采用含維變異算子的云自適應粒子群算法（CAPSODMO）[24]進行求解。

在傳統粒子群算法[21]的基礎上，為了使慣性權重ω的值更好地滿足算法性能要求，本文采用了根據云理論、分子群自適應調整的策略，慣性權重ω的變化規律如下

式中，En決定了正態云模型的陡峭程度；He決定云滴的離散程度；根據3δ準則本文取m1=2.9，m2=10。

針對PSO在算法搜索后期容易陷入局部最優的問題，本文設計的算法在搜索的后期引入了維變異算子，對聚集的粒子賦予變異操作，保持粒子群在搜索過程中的多樣性。維變異通過計算各個粒子當前位置與粒子群質心的距離，來決定是否進行變異。當出現某個粒子當前位置與質心的距離小于0.01時，變異開始；此后在每一次迭代循環中，分別計算各個L(d)的值，d=（1,2,3,…,D），接著找出D個L(d)中值最小的對應所在維，進而對所有粒子的該維以一定概率pm進行變異，使該維的位置重新均勻分布在可行區域[xidmin,xidmax]上，即當rand＜pm時

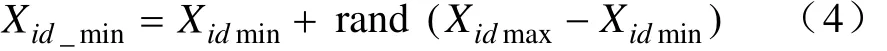
式中，d_min代表需要變異的維；Xid_min為在第d_min維上的位置；rand為[0,1]上均勻分布的隨機數；變異率pm為[0,1]上的常數，本文取pm= 0.2，然后重新獲取新的pbest和gbest位置。

此外，粒子在不斷根據速度調整自己的位置時，還要受到最大速度vmax（取變量搜索空間的50%）的限制；算法的迭代終止條件為達到最大迭代次數；適應度函數為式（1）。

運用本節采取的CAPSO-DMO算法求解UPS電池配置優化的流程如圖1所示。

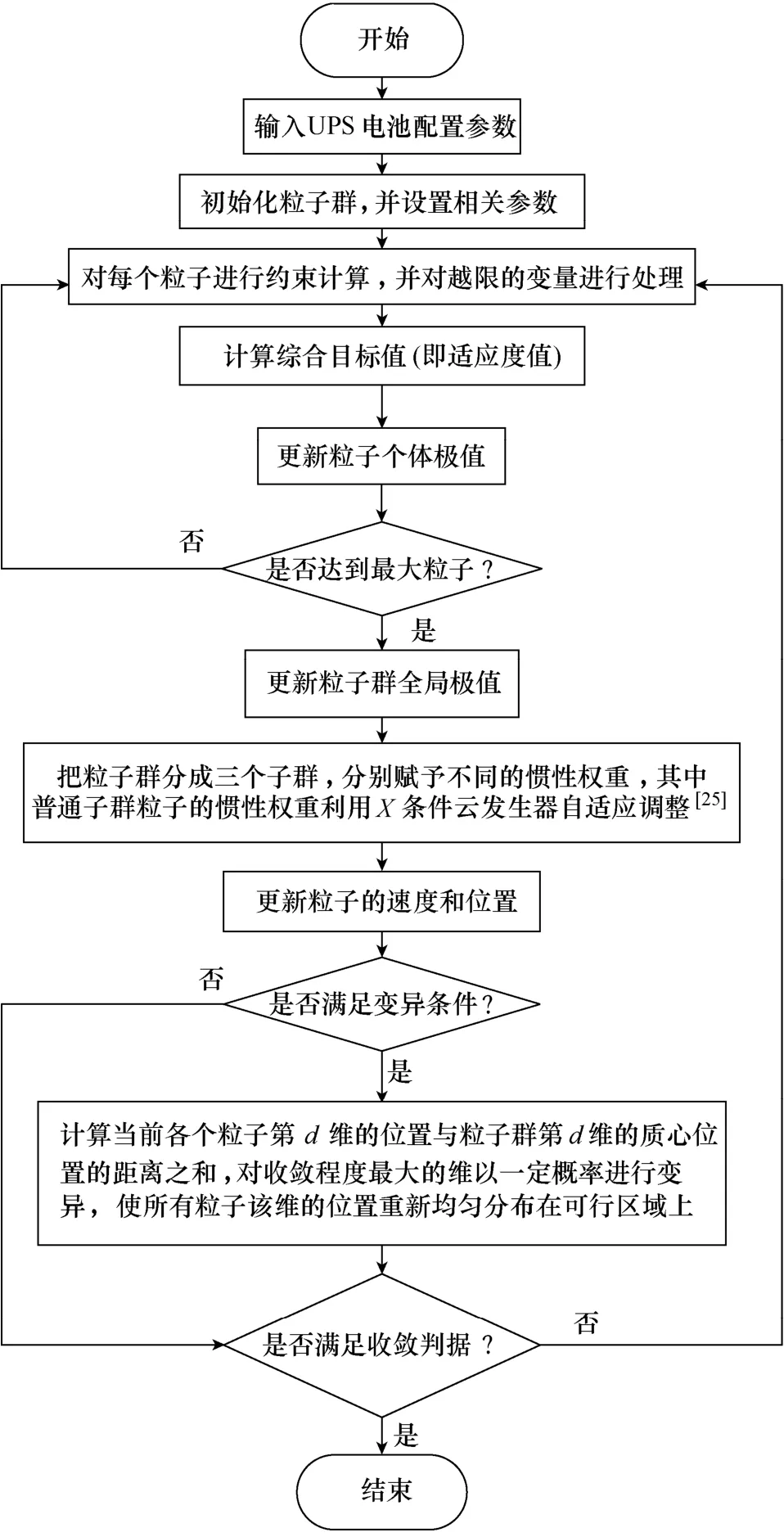
圖1　CAPSO-DMO算法進行UPS電池配置優化計算的流程Fig.1　Flowchart of UPS battery optimal configuration based on CAPSO-DMO algorithm

3　算例與結果分析

如果要設計一個容量為300kV·A的移動式保供電電源UPS，其輸出功率因數為cosφ=0.9，逆變器效率和蓄電池放電效率分別為η=0.9和K=0.95，允許直流電壓范圍為380～600V，額定負荷的供電時間可按30min和15min分別考慮。下面算例中兩個主流品牌的鉛酸蓄電池標稱電壓Ue=2V，終止放電電壓E=1.75V，其他參數見附錄。

本文所用CAPSO-DMO改進粒子群算法對模型有較好的收斂性，一般迭代30次以內則可獲得相應初值下的最優解。為了盡可能減小粒子群算法中隨機參數對結果的干擾，對每一個適應度函數都運算1 000次以期獲得不同初值條件下的最優解。

3.1算例1（美國DEKA UNIGY[28]）

實際應用中可以根據對價格、并聯支路數和重量三個子目標的偏好程度設定不同的權重系數，并獲得相應的最優解。表1中，如首先滿足保供電UPS電源車移動性要求，則選擇直流電壓382V，單一支路，1 280A·h容量的設計方案；若側重經濟性要求，則選擇直流電壓436V，單一支路，1 120A·h容量的設計方案，但電池數目較多，質量較重。針對30min的供電需求，多并聯支路數的設計方案未獲推薦。

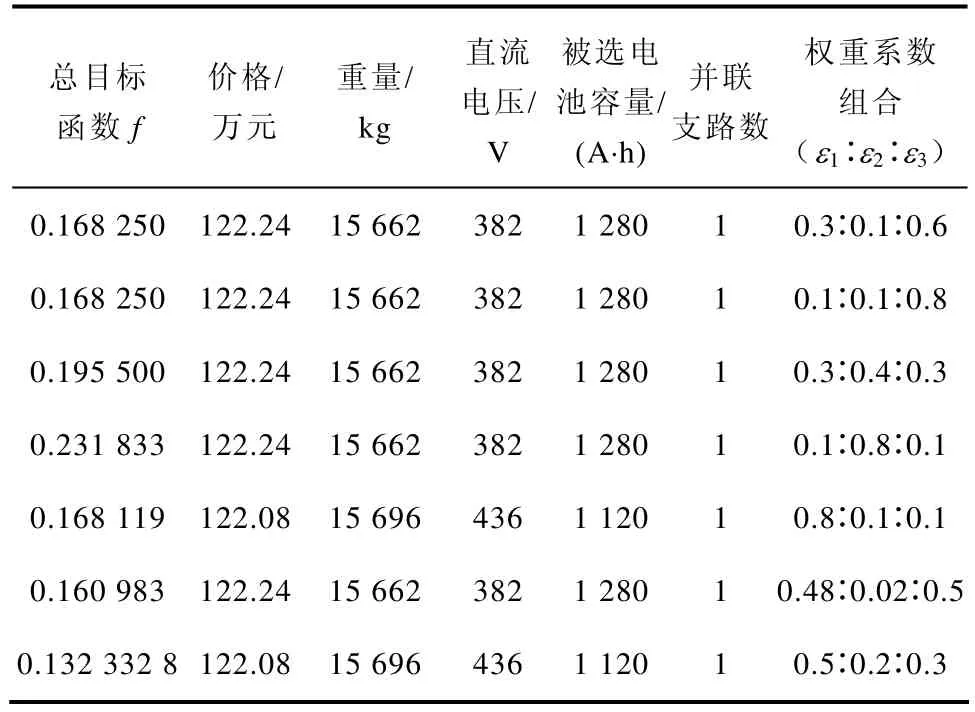
表1　放電時間30min電池最優配置方案Tab.1　Optimal battery configuration schemes for electro-discharge of 30 minutes

針對權重系數組合為0.3∶0.1∶0.6的安排，本文所用的改進粒子群優化算法的收斂性能如圖2所示。圖中僅畫出1 000次運算中能收斂到最優解的搜索過程。可見所用算法雖然每次搜索過程可能不同，但搜索結果是很穩定的，迭代不多于30次便獲得最優解。通過多次運算的工程實際方法可以盡量排除隨機參數對結果的干擾。在其他權重系數組合下，本文方法的收斂性能表現相近，由于篇幅所限，不詳細討論。

圖2　收斂曲線Fig.2　Convergence curves

對于方法的具體實現過程，值得留意的地方是適應度函數中三個子目標獨立規格化的處理。如不規格化子目標，可知電池重量子目標3絕對值較大，且當其權重系數也相對較大時，則此子目標主導了最優解的搜索和最終選擇。原來的設計思路，即通過對不同權重系數組合計算獲得可能分散的最優解集，然后允許決策者依據個人偏好選擇最優方案，則難以實現。為了保證本文優化問題決策的靈活性和自主性，應采用合適的規格化處理方式。如按本文提出的規格化方式，實際上與并聯支路設計子目標2相比，電池重量子目標3的重要性相對不明顯，盡管子目標3的權重系數相對較大。

根據表1及以上的分析可知，若決策者注重優化方案的價格，那么權重系數1ε應該不小于0.5，此時直流電壓相對會較高，所選電池的容量較低，數目較多，方案可靠性相對較低。如要求設計方案質量較輕、安全性較高，那么直流電壓382V的單支路方案為首選，此方案電池數目較少，對應的權重系數1ε＜0.5，其他兩個權重系數可自由組合。

3.2算例2（德國Sonnenschein A600[29]）

在放電時間為15min的條件下，對于不同的權重系數組合，用本文方法獲得的最優解見表2。如要求設計方案質量最輕、價格最低，則需降低對可靠性的要求而采用直流電壓500V的兩支路方案，對應的權重系數1ε、3ε之和應當不小于0.95。當子目標安全可靠性優先考慮時，直流電壓406V的單支路方案成為首選，此時對應的權重系數1ε、3ε之和低于0.95。

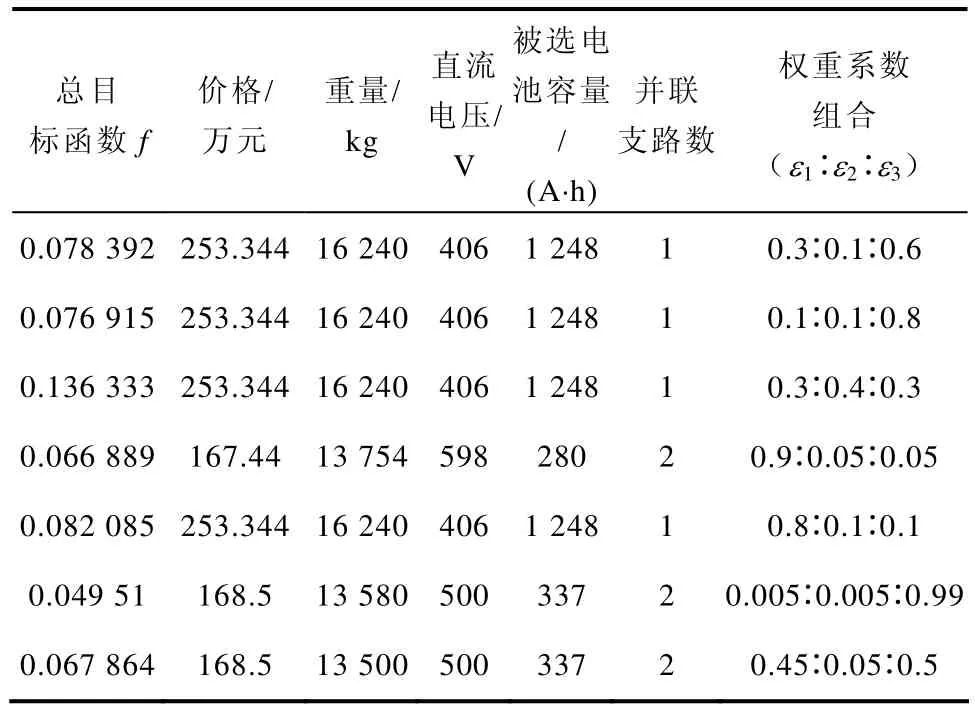
表2　放電時間15min電池最優配置方案Tab.2　Optimal battery configuration schemes for electro-discharge of 15 minutes

4　結論

一個車載式保供電電源儲能部分的設計面臨數量眾多、特性不同的蓄電池選擇問題，需要尋找一個方便高效、保證結果最優或較優的方法。本研究針對電池容量的離散性及有限的條件，并允許UPS的逆變（直流）電壓作為一個可變設計參數，綜合考慮經濟性、并聯設計的安全可靠性以及方案的移動性（重量要求），提出了一個優化UPS電池配置的模型，并采用含維變異算子的云自適應粒子群算法求出優化解集，經過多個算例，證明了該方法的可行性和有效性。方法中通過對不同權重系數組合的最優解集比較分析，允許決策者依據個人偏好選擇最優方案，提高了決策的靈活性和自主性，使得UPS電池配置方案具有代表性。該方法可以為未來供電企業設計以蓄電池（無論是鉛酸蓄電池還是鋰電池）為儲能元件的移動式UPS電源車方案提供一個科學的手段。

附錄

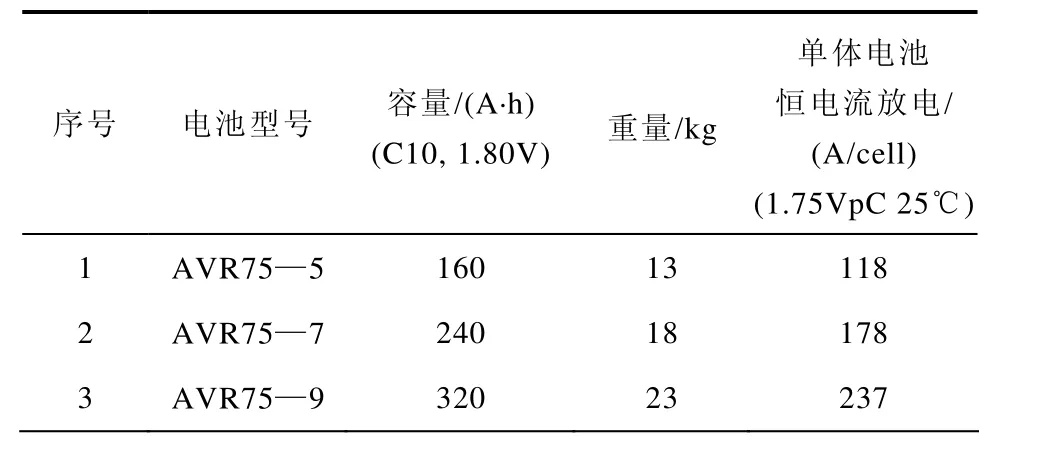
附表1　DEKA Ⅱ系列鋼模架電池規格表（30min）App. Tab.1　The specifications of DEKA Ⅱseries steel frame battery

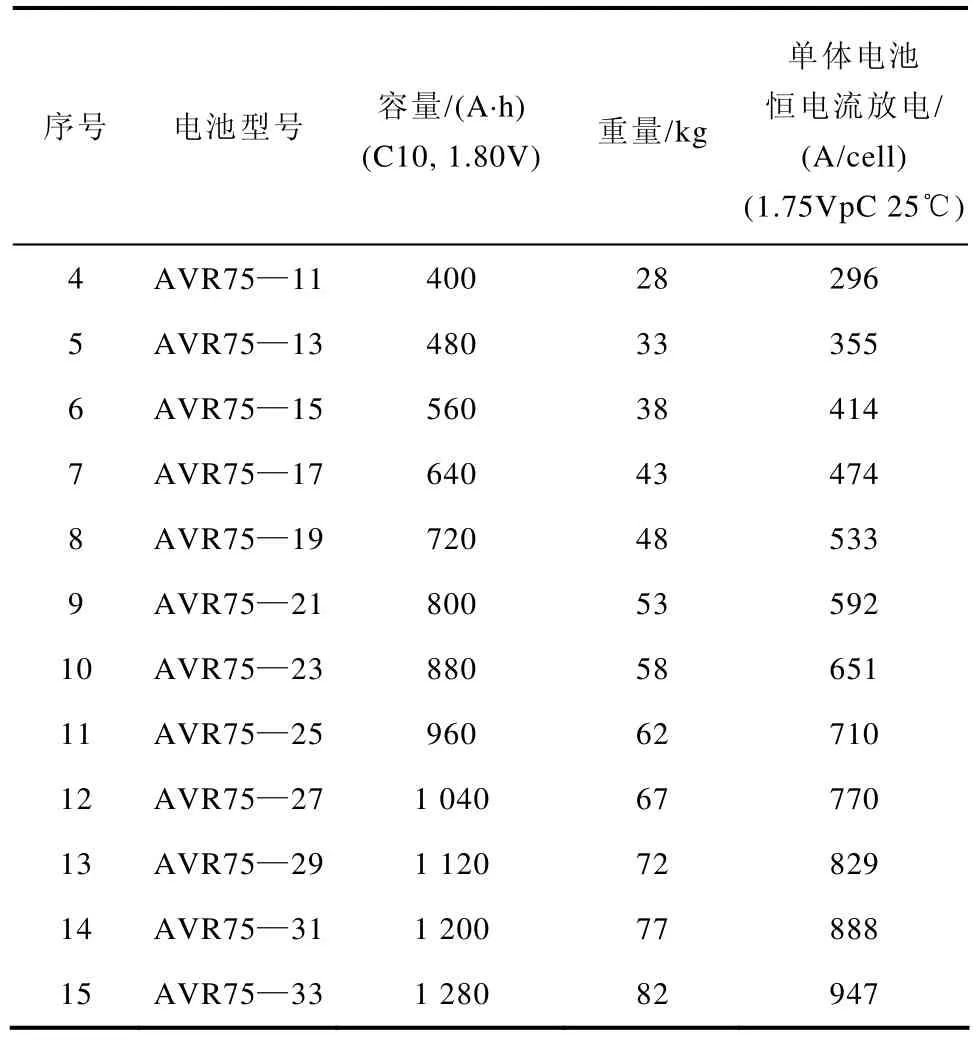
（續）

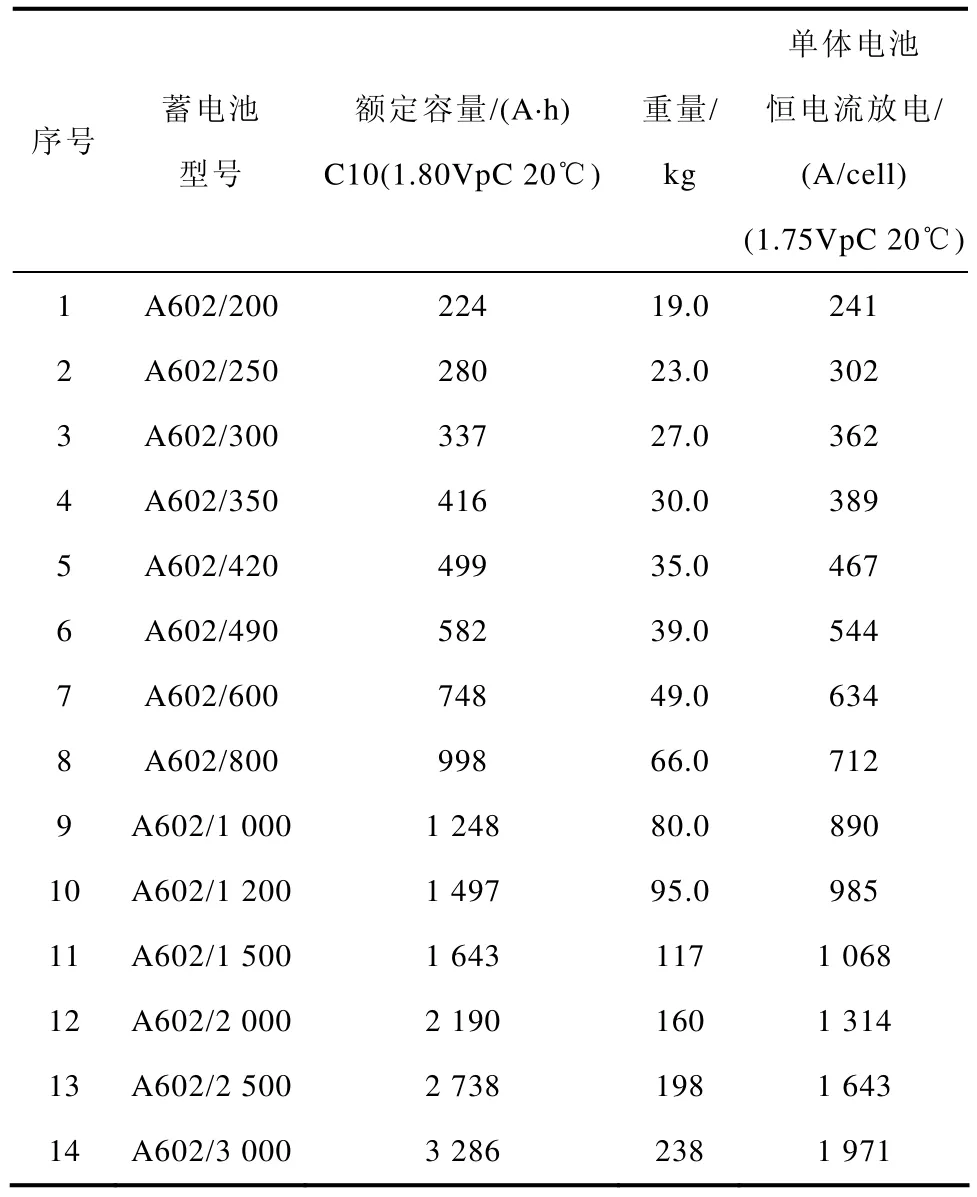
附表2　Sonnenschein A600系列電池規格表（15min）App. Tab.2　The specifications of Sonnenschein A600 series battery

[1] 貴州電網公司. 供電局保供電工作管理標準Q/GZW 21201—2010[S], 2011.

[2] 供配電系統設計規范 GB 50052—2009[S]. 北京:中國計劃出版社, 2010.

[3] 熊雯. 應急供電系統的設計與實現[D]. 成都: 電子科技大學, 2007.

[4] 伏云發, 殷繼彬. 智能化網絡三相UPS系統中的交流旁路電源供電與逆變器電源供電切換裝置的設計[J]. 電源世界, 2002(10): 19-21.

Fu Yunfa, Yin Jibin. The design of switch circuit between bypass power supply and inverter power supply in intelligent network three phase UPS[J]. The World of Power Supply, 2002(10): 19-21.

[5] 不間斷電源設備(UPS), 第3部分：確定性能的方法和試驗要求GB 7260.3—2003[S]. 2003.

[6] 劉勇. UPS蓄電池的選擇與維護[J]. 電源世界, 2010(6): 37-39.

Liu Yong. Selection and maintenance of UPS battery[J]. The World of Power Supply, 2010(6): 37-39.

[7] 楊斌文, 徐穎. UPS用蓄電池的選擇與使用[J]. 機電設備, 2006, 23(2): 6-8.

Yang Binwen, Xu Ying. Selection and usage of the accumulator with UPS[J]. Mechanical and Electrical Equipment, 2006, 23(2): 6-8.

[8] 鄧成博. 磁懸浮飛輪儲能技術UPS及連續供電[J].電源世界, 2008(12): 31-34.

Deng Chengbo. Maglev flywheel energy storage technology in UPS[J]. The World of Power Supply, 2008(12): 31-34.

[9] 陳鳳, 成彬, 王濤, 等. 磁懸浮飛輪儲能設備在UPS系統中的應用研究[J]. 通信電源技術, 2012, 29(2): 1-4.

Chen Feng, Cheng Bin, Wang Tao, et al. The application research on maglev flywheel energy storage technology in UPS system[J]. Telecom Power Technology, 2012, 29(2): 1-4.

[10] 陳峻嶺, 姜新建, 朱東起, 等. 基于飛輪儲能技術的新型UPS的研究[J]. 清華大學學報(自然科學版), 2004, 44(10): 1321-1324.

Chen Junling, Jiang Xinjian, Zhu Dongqi, et al. UPS using flywheel energy storage[J]. Journal of Tsinghua University (Science and Technology), 2004, 44(10): 1321-1324.

[11] 薛金會. 基于超級電容儲能的光伏發電系統研究[D]. 北京: 華北電力大學, 2008.

[12] 佟明斯. 超級電容型動力UPS的儲能技術研究[D].哈爾濱: 哈爾濱工業大學, 2011.

[13] 張靖. 超級電容蓄電池復合電源的研究與仿真[D].武漢: 武漢理工大學, 2005.

[14] 高志剛, 冬雷, 廖曉鐘. 一種帶儲能功能的新型光伏并網逆變器研究[J]. 電網技術, 2012, 36(11): 36-40.

Gao Zhigang, Dong Lei, Liao Xiaozhong. A novel grid-integrating inverter with energy storage capability for PV generation system[J]. Power System Technology, 2012, 36(11): 36-40.

[15] 侯世英, 房勇, 孫韜, 等. 混合儲能系統在獨立光伏發電系統功率平衡中的應用[J]. 電網技術, 2011, 35(5): 183-187.

Hou Shiying, Fang Yong, Sun Tao, et al. Application of hybrid energy storage system in power balance of stand-alone photovoltaic power system[J]. Power System Technology, 2011, 35(5): 183-187.

[16] 侯朝勇, 胡學浩, 惠東. 鋰電池儲能并網變換器的設計與實現[J]. 電網技術, 2012, 36(3): 246-251.

Hou Chaoyong, Hu Xuehao, Hui Dong. Design and implementation of grid-connected converter for lithium battery energy storage system[J]. Power System Technology, 2012, 36(3): 246-251.

[17] 黃平. 粒子群算法改進及其在電力系統的應用[D].廣州: 華南理工大學, 2012.

[18] 玄光南, 程潤偉. 遺傳算法與工程優化[M]. 于歆杰, 周根貴, 譯. 北京: 清華大學出版社, 2006.

[19] 王兆安, 劉進軍. 電力電子技術[M]. 北京: 機械工業出版社, 2010.

[20] Kennedy J, Eberhart R. Particle swarm optimization[C]. Proceedings of IEEE International Conference on Neural Networks，Perth，Australia，1995，4：1942-1948.

[21] 袁曉輝, 王乘, 張勇傳, 等. 粒子群優化算法在電力系統中的應用[J]. 電網技術, 2004, 28(19): 15-19.

Yuan Xiaohui, Wang Cheng, Zhang Yongchuan, et al. A survey on application of particle swarm optimization to electric power systems[J]. Power System Technology, 2004, 28(19): 15-19.

[22] 金欣磊. 基于PSO的多目標優化算法研究及應用[D]. 杭州: 浙江大學, 2006.

[23] 莊夏, 戴敏, 何元清. 基于改進粒子群優化LSSVM的飛機發動機故障診斷[J]. 實驗技術與管理, 2013, 30(2): 54-57.

Zhuang Xia, Dai Min, He Yuanqing. Fault diagnosis for aero-engine based on improved particle swarm algorism optimizing support vector machine[J]. Experimental Technology and Management, 2013, 30(2): 54-57.

[24] 陳曾. 基于粒子群—內點混合算法的無功優化研究[D]. 廣州: 華南理工大學, 2013.

[25] 韋杏瓊, 周永權, 黃華娟. 云自適應粒子群算法[J].計算機工程與應用, 2009, 45(1): 48-50.

Wei Xingqiong, Zhou Yongquan, Huang Huajuan. Adaptive particle swarm optimization algorithm based on cloud theory[J]. Computer Engineering and Applications, 2009, 45(1): 48-50.

[26] 付國江, 王少梅, 劉舒燕. 含維變異算子的粒子群算法[J]. 武漢大學學報, 2005, 38(4): 79-82.

Fu Guojiang, Wang Shaomei, Liu Shuyan. A PSO with dimension mutation operator[J]. Engineering Journal of Wuhan University, 2005, 38(4): 79-82.

[27] 杜兆斌, 鄧桂萍, 席云華. 大型移動保供電電源儲能元件選型分析[J]. 機電工程技術, 2013, 42(9): 47-50.

Du Zhaobin, Deng Guiping, Xi Yunhua. Selection of energy-storage battery of mobile large-capacity power source for power supply ensuring of users[J]. Mechanical & Electrical Engineering Technology, 2013, 42(9): 47-50.

[28] EAST PENN Manufacturing co. inc. http://www. dekabatteries.com.

[29] Germany Sonnenlicht Industrial Group (China) Co., limited. http://www.sonnenlichtcn.com/.

Energy-Storage Battery Optimal Configuration of Mobile Power Source for Power Supply Ensuring of Users

Du Zhaobin1Chen Zeng1Guan Lin1Xi Yunhua2Huang Ping1Huang Yaopeng1
（1. South China University of TechnologyGuangzhou510640China
2. Guangzhou Electric Power Design InstituteGuangzhou510620China）

The high quality demand of power supply urges the continuous service development in power supply ensuring of users. The flexible and reliable power source technology is the key to satisfy the actual demand. This paper proposes an energy-storage battery optimal configuration model of mobile power source, namely UPS (uninterrupted power supply), in which economical efficiency, safe reliability of paralleling design, and mobility (weight index) are all taken into account as the design targets. The model considers the discreteness and restriction of battery capacity, as well as UPS inverted voltage variability within a reasonable range. The method of cloud adaptive particle swarm optimization including dimension mutation operator is used for optimal allocation scheme solution. The examples demonstrate the feasibility and effectiveness of the proposed model and method.

Power supply ensuring of users, mobile power source, storage battery, multi-objective, particle swarm optimization, dimension mutation, cloud theory

TM76

杜兆斌男，1977年生，博士，講師，主要從事電力系統運行與穩定、電網規劃研究等。

管霖女，1970年生，博士，教授，主要研究方向為電力系統穩定與控制、電網規劃和可靠性、人工智能應用技術等。

國家自然科學基金（51577071）和廣東省自然科學資金（2015A030313202）資助項目。

2014-05-05改稿日期 2014-08-07