單矢量水聽器估計目標方位的方法與實驗?

笪良龍　侯文姝　孫芹東　王文龍

（海軍潛艇學院　青島　266071）

單矢量水聽器估計目標方位的方法與實驗?

笪良龍侯文姝?孫芹東王文龍

（海軍潛艇學院青島266071）

為評估基于單矢量水聽器的方位估計能力，在黃海海域對矢量水聽器進行實驗。矢量水聽器吊放于接收船尾部，采用平均聲強器和復聲強器方位估計方法，并提出以概率密度值最大的方位角作為目標方位估計值的具體處理準則，對恒定方向、勻速行駛的目標船方位進行估計，并求出兩種方法的方位估計誤差。結果表明，水聽器布放深度10 m時，對正橫距離為0.42 km的航速10 kn的目標船，平均聲強器方法的水平方位角估計誤差18°，極角估計誤差為5°，可以在離目標船最遠1.17 km處估計其方位；復聲強法的水平方位角估計誤差為13°，極角估計誤差為8°，可以在離目標船最遠2.35 km處估計其方位。在有接收船的噪聲干擾情況下，復聲強器比平均聲強器方法估計的方位更準確，可以對更遠處的噪聲源進行方位估計。

方位估計，矢量水聽器，平均聲強器，復聲強器

1　引言

單矢量水聽器同步共點測量聲壓和質點振速矢量［1］，可有選擇地抑制離散干擾噪聲源發出的噪聲，有效定位噪聲目標［2］。相對傳統水聽器陣，單矢量水聽器有4個共點陣元，可獲得更高增益，有效抗“左右舷模糊”。且單矢量水聽器體積小、功耗低，可應用于海上分布式智能系統的輕型節點或移動節點，如浮標、潛標和AUV［1］。而這些節點均對要求解算目標角度的算法計算量小，易于在硬件上實現。單矢量水聽器方位估計算法主要有平均聲強器方位估計和復聲強器方位估計方法［3-4］，又稱為時域和頻域［1］兩種方式。平均聲強器方位估計優點是可以處理寬帶信號，如處理艦船的噪聲信號［5］，缺點是無法對多個寬帶信號源進行方位估計；復聲強器方位估計，優點是利用聲壓和振速有效估計窄帶信號的方位，缺點是無法有效估計寬帶噪聲信號的方位。

文獻［5］設計了矢量水聽器座底，單目標近距離直航運動的海上實驗，采用平均聲強器方位估計和柱狀圖方位估計方法，驗證了柱狀圖方位估計方法抑制強線譜相干干擾的有效性；文獻［1］采用這兩種方法，用WilcoxinTV-001型［6］矢量水聽器在淺海環境下可以對2 km遠的緩慢移動高頻聲源進行定位追蹤。

平均聲強器和復聲強器方位估計方法適于作為海上分布式智能系統的輕型或移動節點的核心算法［1］。本文采用平均聲強器和復聲強器方位估計方法，分別對單矢量水聽器接收的海上試驗數據進行了目標方位估計，然后采用概率密度值最大的方位角作為估值的方位估計準則，求出兩種方法的誤差并進行誤差分析。

2　目標方位估計原理

矢量水聽器在聲場給定點處同時提供聲壓p（t）和振動加速度矢量的三個正交分量｛ax（t），ay（t），az（t）｝的樣本。將振動加速度轉換為相應的振速分量v（t）｛vx（t），vy（t），vz（t）｝，以單矢量水聽器所在位置為三維直角坐標系原點O，坐標系x，y軸在水平平面，z軸正方向是從海面垂直指向天空。設振動加速度分量的正方向與直角坐標系三個軸向重合，如圖1所示。

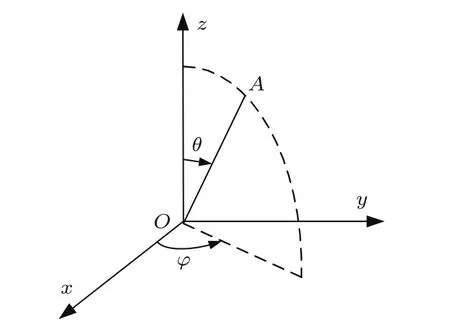
圖1　矢量水聽器的方位角示意圖Fig.1 Sketch map of angle of vector hydrophone

設目標位于A點，矢量水聽器用水平方位角φ和極角θ估計目標方位。取值范圍分別為［0，2π）和［0，π］。在測點的振速矢量為

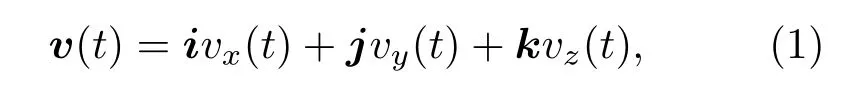
其中，振速分量與振速的關系是［4］

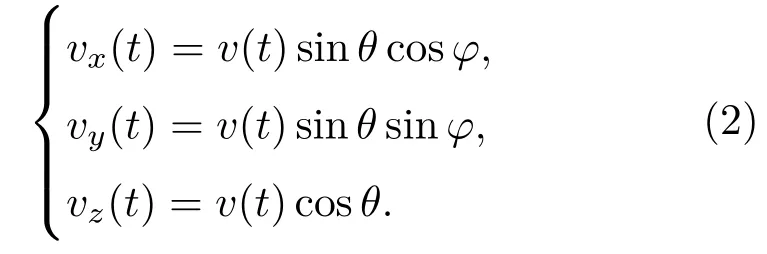
2.1平均聲強器方位估計方法

矢量聲強為［7］

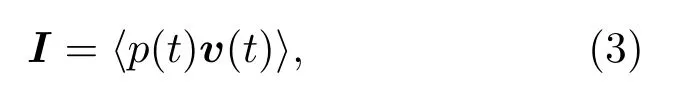
其中p（t）和v（t）是聲壓和質點振速的瞬時值，括號代表多樣本統計平均。

將表達式（1）代入表達式（3）：

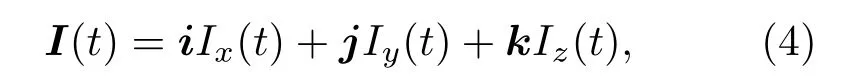
根據表達式（2）得水平方位角和極角為［7］

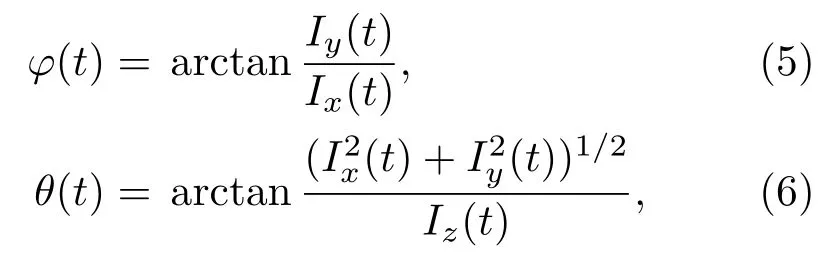
其中，Ii（t）=〈p（t）vi（t）〉，i=x，y，z。

數據總時間長度為T1，采樣頻率為fs。每隔T2時間長度，對長為T3（T3≥T2）的聲壓p（t）和振速vi（t）相乘。根據式（5）和式（6）求出φ（t）和θ（t）。

2.2復聲強器方位估計方法

聲壓和振速的互譜為［7］

其中，i=x，y，z。

能流密度矢量I在坐標軸i（i=x，y，z）方向的分量Ii的頻域表達為［7］

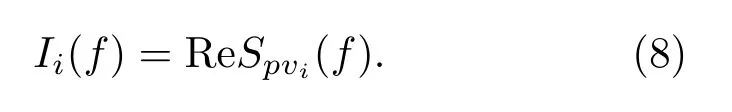
在頻率f處，矢量水聽器估計的水平方位角和極角為［7］

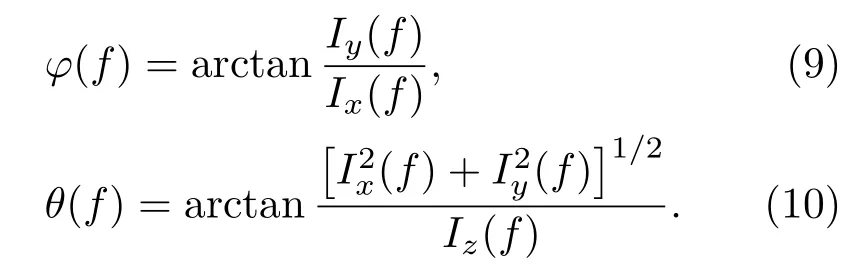
由于聲壓振速互譜的方法屬于頻域的方式，主要用于處理窄帶信號，所以在研究頻率時取工作頻率范圍內的一段窄帶頻譜作為分析頻帶。用滑動時間窗作互譜分析。數據總時間長度為T1，采樣頻率為fs。每隔T2時間長度，對聲壓和振速作FFT，FFT樣本窗長為T3（T3≥T2）。取分析頻帶范圍內的頻譜P（f）和Vi（f），根據式（9）和式（10）求出分析頻帶范圍內的φ（f）和θ（f）。

2.3方位角估計準則

以水平方位角為例，將其取值范圍為［0，2π］劃分為n段分割區，第i段分割區對應［（i-1）× 2π/n，i×2π/n］，取分割區的中心方位值為φi=（i-1）×2π/n，對于T4（T4≥T2）時間長度分析頻帶內的φ（f），求出水平方位角第i段概率密度頻數F（φi）。提出該時間長度的矢量水聽器坐標系下水平方位角的估值為：概率密度頻數F（φi）最大值對應的角度值，即?φ滿足：

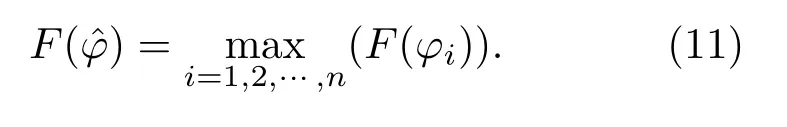
表達式（11）的準則所給出的估值是實測值，記為準則1，與文獻［4］的聲壓、振速互譜方位直方圖估計方法中的直方圖統計平均法不同。文獻［4］的方法采用方位的期望值，在此記為準則2。

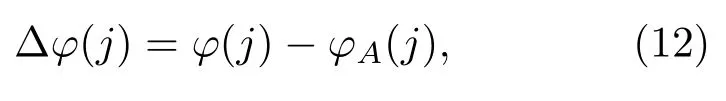
N個時刻水平方位角估計的統計誤差為

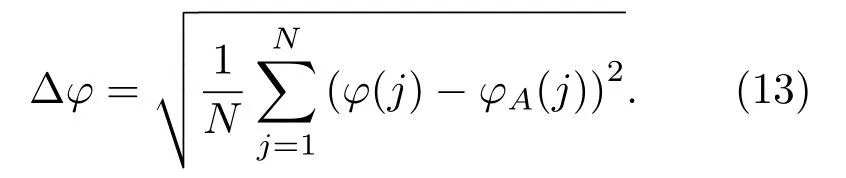
3　海上試驗

2014年9月在黃海某海域進行海上試驗，吊放矢量水聽器陣接收遠處的船噪聲，獲取矢量水聽器測向特性。接收船和目標船的吃水深度均為3 m左右。實驗區域水深55 m，海況1級，附近有漁船干擾。

3.1試驗設計

實驗采用單矢量水聽器中的復合同振式矢量水聽器，由零階換能器（聲壓水聽器）和二階換能器（三分量振動加速度水聽器）組成，主要參數為：密度為1.20 g/cm3，尺寸為?60 mm×78 mm，聲壓靈敏度為-192.7 dB（0 dB=1 V/μPa），加速度x通道1000 Hz的靈敏度為-178.5 dB。矢量水聽器設計工作頻率為20 Hz～5 kHz。工作頻率上限對應于最小波長λmin=0.3 m，該矢量水聽器的直徑D≤0.025 m，滿足條件D≤λmin/3。

海上吊放五元矢量水聽器陣的現場情況如圖2所示。在接收船尾吊放水聽器，單個矢量水聽器輸出的4路信號經過水密罐的前級放大電路（放大10倍）和前級濾波（帶通濾波，通帶20 Hz～5 kHz）后，通過矢量水聽器多通道測量系統將各個矢量水聽器的4路信號分離，進行二級濾波（濾除70 Hz以下頻段），最后通過NI采集設備進行采集（采樣頻率為20 kHz）。

圖2　海試布放矢量水聽器陣Fig.2 The vector hydrophone array is dipped into the sea

目標船相對矢量水聽器的通過路徑如圖3所示。接收船B的發動機關閉，在O點布放矢量水聽器，水聽器布放深度為水下10 m。目標船A沿圖示方向直航，速度10 kn。矢量水聽器和目標船之間最小距離為OC（即正橫距離）。

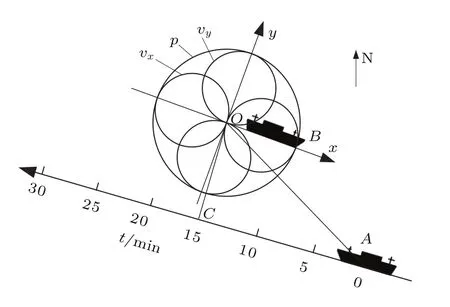
圖3　目標船相對矢量水聽器的通過路徑圖Fig.3 Route map of the target vessel passing the vector hydrophone

地理坐標系下目標船A和接收船B的基本情況如圖4所示。圖4（a）為理論計算得到的目標船的極角θA，其變化小于1°。根據目標船和接收船實時測量GPS數據得水平方位角φA和距離dOA，如圖4（b）和4（c）所示。圖4（b）表示目標船φA從337°減小至166°。圖4（c）表示目標船A從距O點5.45 km處出發，在15 min時到達水聽器正橫方向，正橫距離OC為0.42 km。接收船B的水平方位角φB如圖4（d）所示。試驗期間，雖然接收船發動機關閉，沒有螺旋槳噪聲，但是水聽器布放于接收船尾水深10 m處，接收船水動力噪聲和機械噪聲對矢量水聽器干擾很大。矢量水聽器振速x通道正方向在水平方向上指向船艏，根據水聽器實時姿態測量結果，將矢量水聽器振速x通道正方向轉換為地理坐標系下的水平方位角，作為接收船B的水平方位角φB。接收船的水平方位角φB在地理坐標系下342°方向波動，波動幅度小于7°。接收船的極角θB是未知的，水聽器位于接收船尾水深10 m處，接收船長100 m左右，吃水深度3 m，海浪拍打船體產生的噪音位置是不確定的，則水聽器估計接收船的極角θB在0°～86°范圍內。

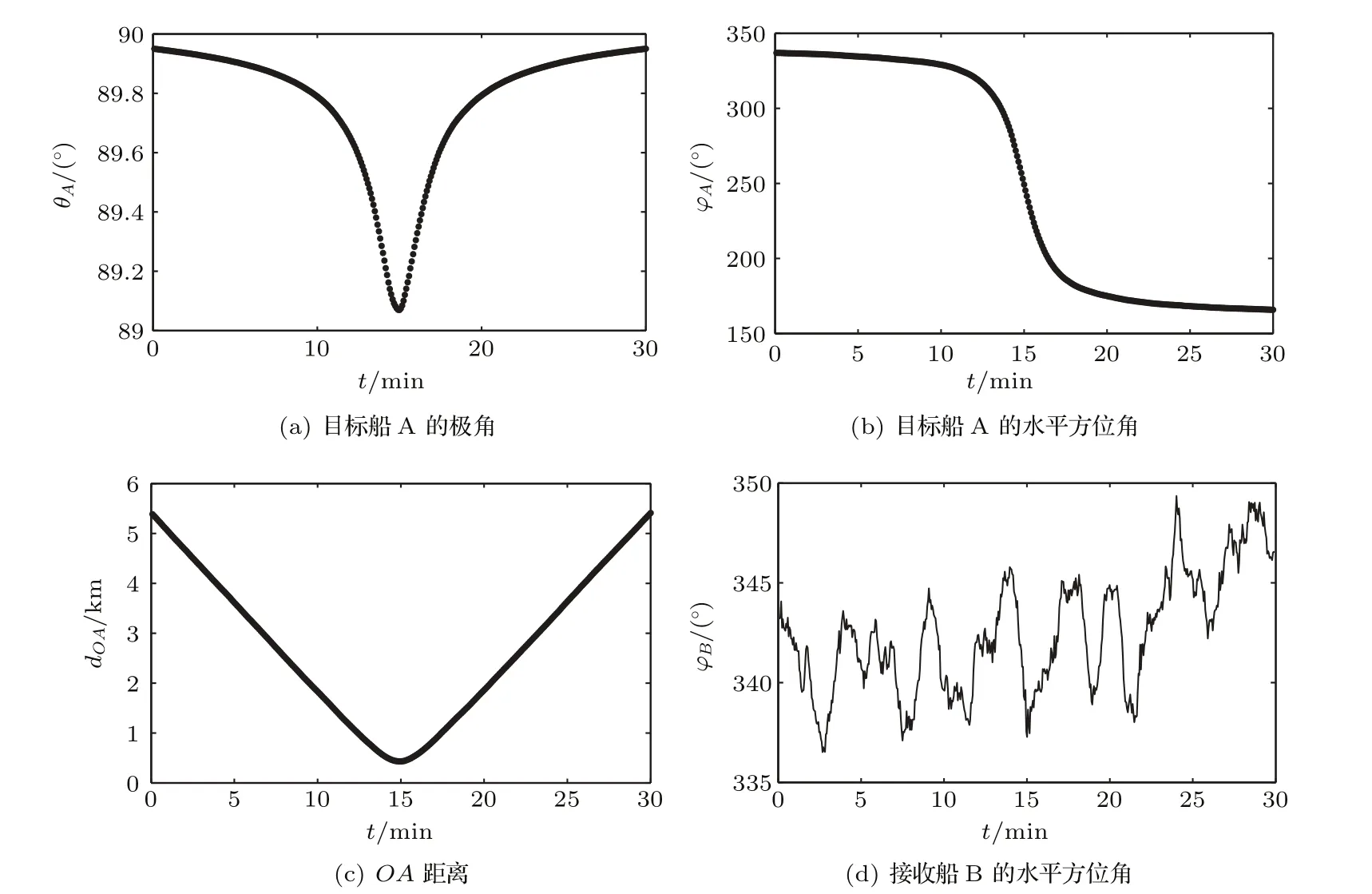
圖4　地理坐標系下目標船A和接收船B的基本情況Fig.4 Basic information of ship A and ship B under the geographic coordinate system

矢量水聽器陣的各通道聲譜圖如圖5所示，分別是聲壓和振速通道在70～5000 Hz頻帶內0～30 min的功率譜（dB re 1μPa2/Hz），平均時間6 s，分析帶寬1.2 Hz（每2 s進行16384點FFT，對6 s數據取平均）。在圖5中，每個通道均可以看到兩處寬帶運動聲源干涉條紋，在0～8 min和12～18 min時間范圍內。聲壓通道的干涉譜線最明顯，這是由該通道的靈敏度全向性決定的。結合聲壓通道譜線特性和目標船在15 min通過水聽器正橫方向的信息，可以確定第2處干涉譜線是目標船產生的。振速x（vx）通道的譜線在15.5 min時較弱，圖3表示此時目標船到達vx通道靈敏度指向性極小值方向，因此該通道此時收到的信號最弱。此時vy通道在這一時刻譜的強度是三個振速通道中最強的，因為目標船到達vy通道靈敏度指向性最大值方向。由于目標船在試驗過程中沿直線行駛，第一處干涉譜線不是目標船產生的，判定是近處的漁船產生的。圖5中可以看到600 Hz～2000 Hz頻段范圍內明顯的干涉條紋，是目標船主要的輻射噪聲頻段，復聲強器方法選取該頻帶作為分析頻帶。

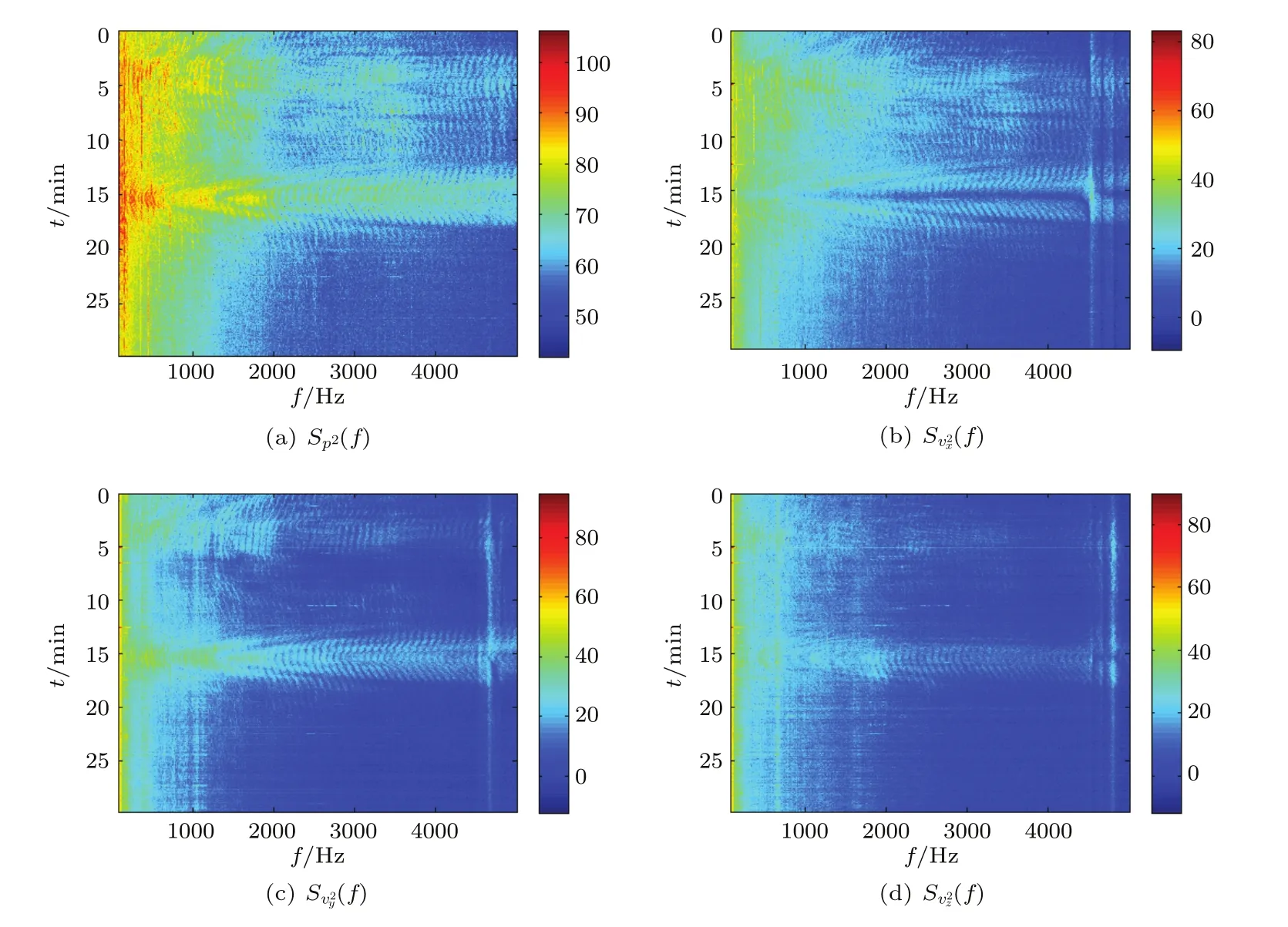
圖5　矢量水聽器的各通道聲譜圖Fig.5 The spectrogram of each channel of the vector hydrophone

實驗用水聽器振速通道采用加速度傳感器，需要將振動加速度轉換為振動速度才能進行方位角估計。在轉換過程中，如果直接對加速度數據積分，將會出現類似偏置帶來的影響，分析是實測數據中10 Hz以下的直流分量造成的影響，需要濾除。由于300 Hz以下主要是遠處航船噪聲，且強度較大，對估計近處的艦船目標水平方位角有較大的不利影響，因此濾除300 Hz以下的信號。實驗過程中，只有2號、4號和5號水聽器所有通道正常工作，依次記為VS1（Vector sensor 1）～VS3。

下面設置兩種方位估計方法的基本參數。數據總時間長度為30 min，采樣頻率為fs=20000 Hz。每10 s取T1=1 s數據進行分析。數據處理時間長度示意圖如圖6所示。在T1內，每T2=0.005 s取 T3=0.0512 s（T3≥T2）長度的聲壓和振速時域數據，采用平均聲強器方位估計方法處理。對樣本窗長1024點（即T3=0.0512 s（T3≥T2）長度）數據進行復聲強器方位估計方法處理。兩種方法的樣本統計時間長度均為T4=0.25 s。

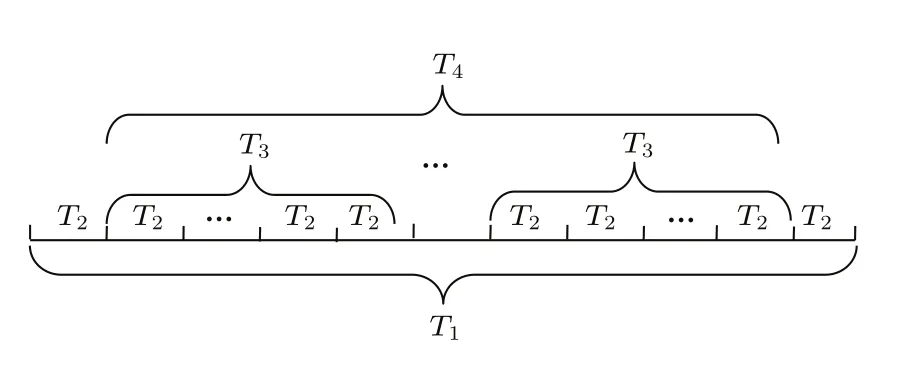
圖6　數據處理時間長度示意圖Fig.6　The diagram of time length of data processing

將水平方位角φ取值范圍［0，2π］劃分為360段，將極角θ取值范圍［0，2π］劃分為180段。則T4時間長度內，平均聲強器方位估計方法樣本數為T4/T3=50。復聲強器分析頻帶600 Hz～2000 Hz內的頻點數為72，復聲強器方位估計方法樣本數為（T4/T3）×72=3600。

3.2平均聲強器方位估計方法

平均聲強器方位估計方法獲得的水聽器坐標系下VS1的極角和水平方位角時間歷程圖如圖7所示。圖7（b）是取T4時間長度內的50個φ（t）樣本，統計求出水平方位角概率密度頻數F（φ）。圖7（a）和圖7（b）的0～20 min，平均聲強器方位估計方法在艦船噪聲方向的概率密度頻數都顯著高于其它方向。

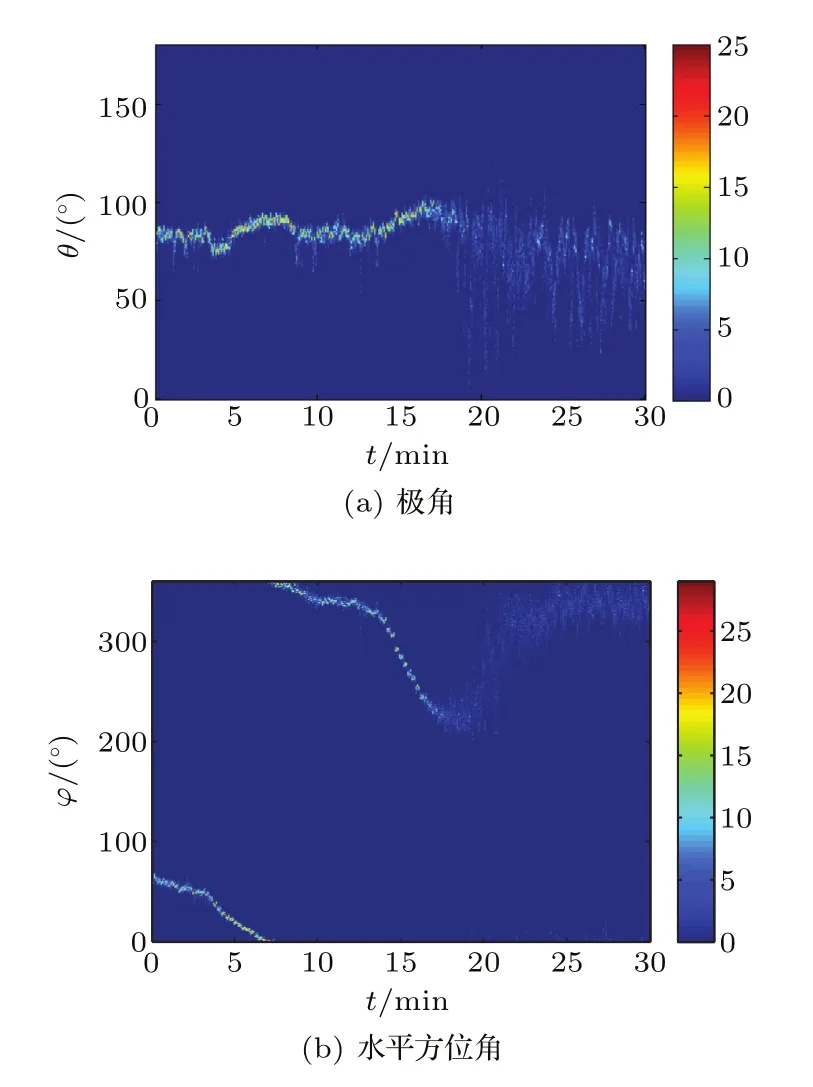
圖7　平均聲強器方位估計方法獲得的VS1的極角和水平方位角時間歷程圖Fig.7 Time course of azimuth by acoustic intensity averager of VS1

平均聲強器方位估計方法按準則1獲得的VS1在地理坐標系下的極角和水平方位角如圖8所示。在圖8（a）和圖8（b）中，用藍點表示水聽器VS1按表達式（11）的準則1估計的極角θ和水平方位角φ，用紅點線表示目標船A的理論極角θA和GPS實測水平方位角φB。接收船的極角θB應當在0°～86°范圍內隨機變化，無法在圖8（a）中繪制，圖8（b）中黑線是接收船的水平方位角。圖8（a）中極角在0～18 min較好地與90°方向吻合，而18～30 min極角在0°～ 100°范圍內變化。可以初步判定0～18 min主要是非接收船的艦船噪聲信號，而之后主要是接收船噪聲信號。圖8（b）中，由于0～8 min時有漁船干擾，無法判斷水聽器正確估計目標船的起始時刻。但是正確估計目標船的終止時刻和目標船通過正橫方向的時刻可以反推起始時刻。20～30 min主要是接收船噪聲信號。由于15 min時目標船到達正橫方向，相應的，在0～8 min不是目標船的方位信息。0～8 min，水平方位角φ從60°減小至0°進而從360°減小至340°，應當是漁船的水平方位角。

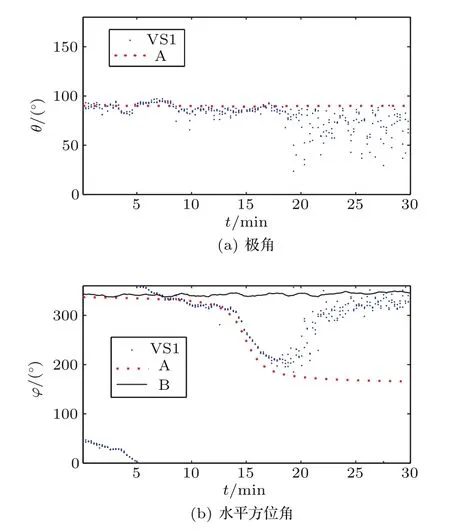
圖8　平均聲強器方位估計方法按準則1獲得的VS1的極角和水平方位角時間歷程圖Fig.8 Time course of azimuth by acoustic intensity averager of VS1 according to criterion 1

平均聲強器方位估計方法按準則2獲得的VS1在地理坐標系下的極角和水平方位角如圖9所示。與圖8準則1結果相比，兩者的變化趨勢大體一致。但是準則2在7～8 min處圖7（b）從0°變為360°時，圖9（b）得到的是兩者水平方位角的期望值，處于0°～340°，而實際中并不存在該方向的目標。

平均聲強器方位估計方法按準則1獲得的VS1—VS3的極角和水平方位角如圖10所示，3個水聽器的估計結果基本一致。

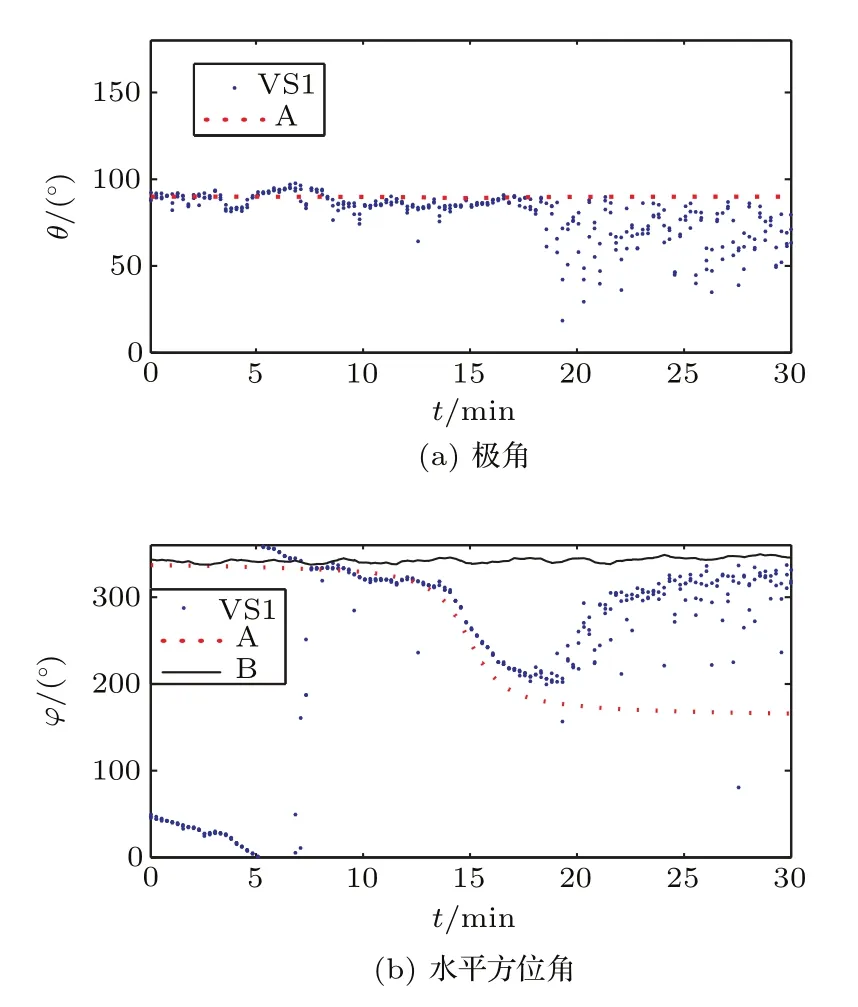
圖9　平均聲強器方位估計方法按準則2獲得的VS1的極角和水平方位角時間歷程圖Fig.9 Time course of azimuth by acoustic intensity averager of VS1 according to criterion 2

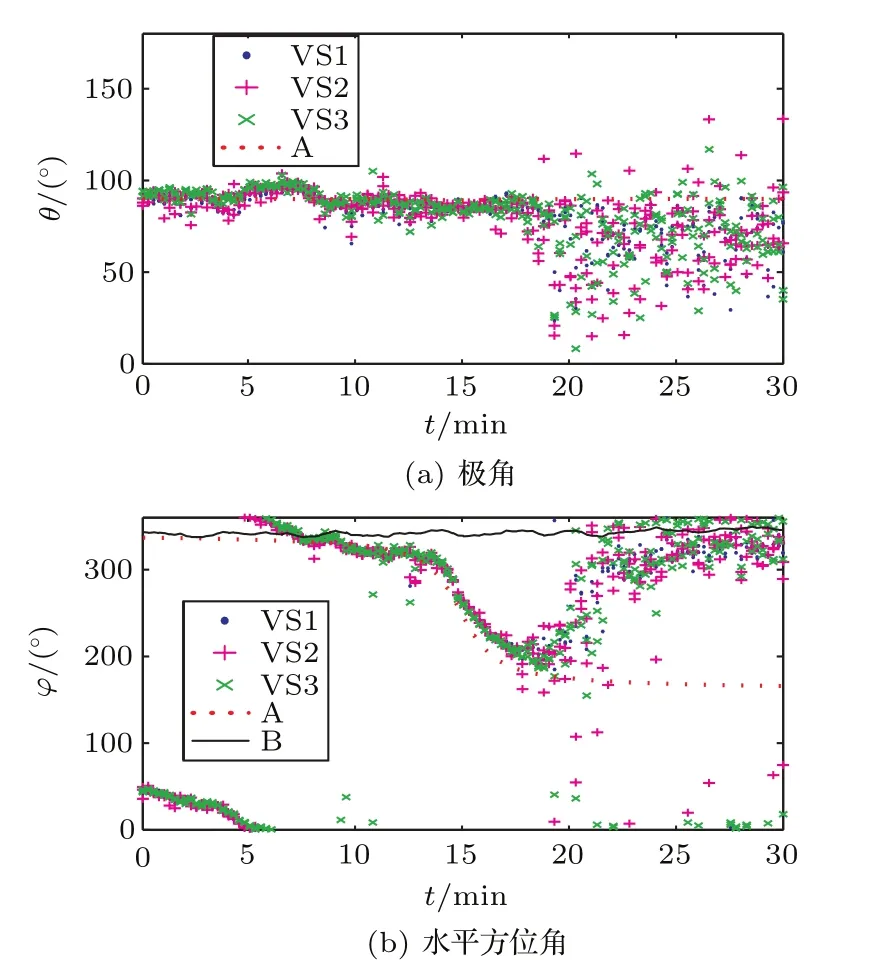
圖10　平均聲強器方位估計方法按準則1獲得的VS1-VS3的極角和水平方位角時間歷程圖Fig.10 Time course of azimuth by acoustic intensity averager of VS1—VS3 according to criterion 1

3.3復聲強器方位估計方法

復聲強器方位估計方法獲得水聽器坐標系下的VS1的極角和水平方位角時間歷程圖如圖11所示，0～8 min的漁船方位信號比10～20 min的目標船方位信號強，可能是漁船的距離較近，噪聲較強造成的。

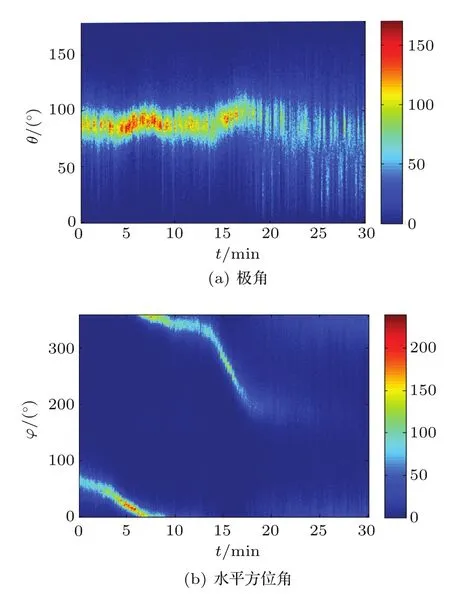
圖11　復聲強器方位估計方法獲得的VS1的極角和水平方位角時間歷程圖Fig.11 Time course of azimuth by complex acoustic intensity method of VS1

復聲強器方位估計方法按準則1獲得的VS1在地理坐標系下的極角和水平方位角如圖12所示，圖12中所有標示與圖8相同。分析頻帶取600 Hz～2000 Hz。圖12（b）VS1估計的方位角在21.5 min處“斷開”，8～21.5 min與目標船A的水平方位角吻合的較好，21.5～30 min水平方位角與接收船B的方位吻合。20～30 min極角也符合對接收船B的估計，處于0°～86°這個范圍內。

平均聲強器方位估計方法按準則2獲得的VS1在地理坐標系下的極角和水平方位角如圖13所示。與圖12準則1結果相比，兩者的水平方位角變化只有在目標船通過正橫距離附近相同。在5～14 min處，圖13（b）的水平方位角從0°變為300°，均存在0°的數據，因此圖13（b）采用準則2得到的是漁船和目標船A水平方位角的期望值，是一組并不存在的方位。在20～30 min得到的方位看似和目標船A相吻合，但是根據圖11（b）可知這只是將0°和360°左右的水平方位角估值平均得到的，是一種巧合。

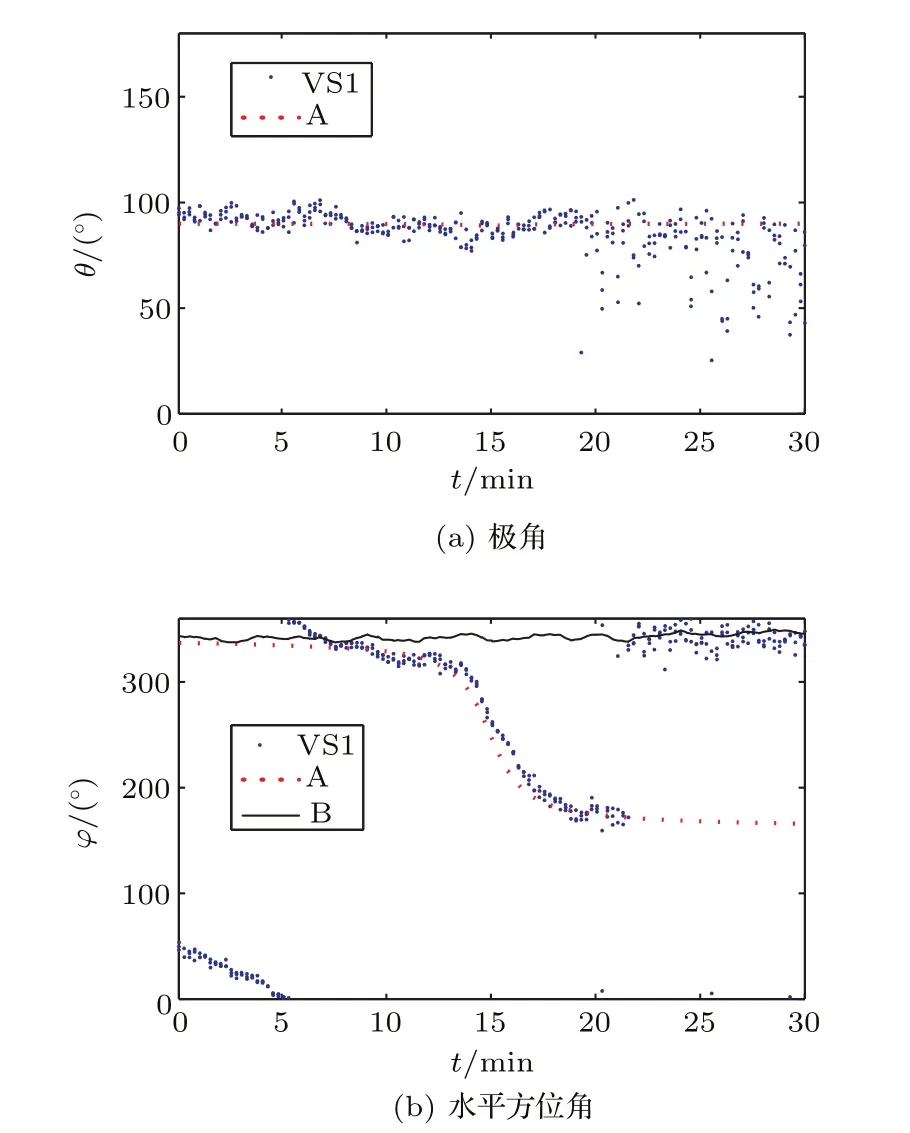
圖12　復聲強器方位估計方法按準則1獲得的VS1的極角和水平方位角時間歷程圖Fig.12 Time course of azimuth by complex acoustic intensity method of VS1 according to criterion 1

圖13　復聲強器方位估計方法按準則2獲得的VS1的極角和水平方位角Fig.13 Time course of azimuth by complex acoustic intensity method of VS1 according to criterion 2

平均聲強器方位估計方法按準則1獲得的VS1-VS3的極角和水平方位角如圖14所示。三個水聽器的估計結果基本一致，較小的差別可能是由于水聽器安裝和布放后三者的水聽器坐標系未完全重合造成的。

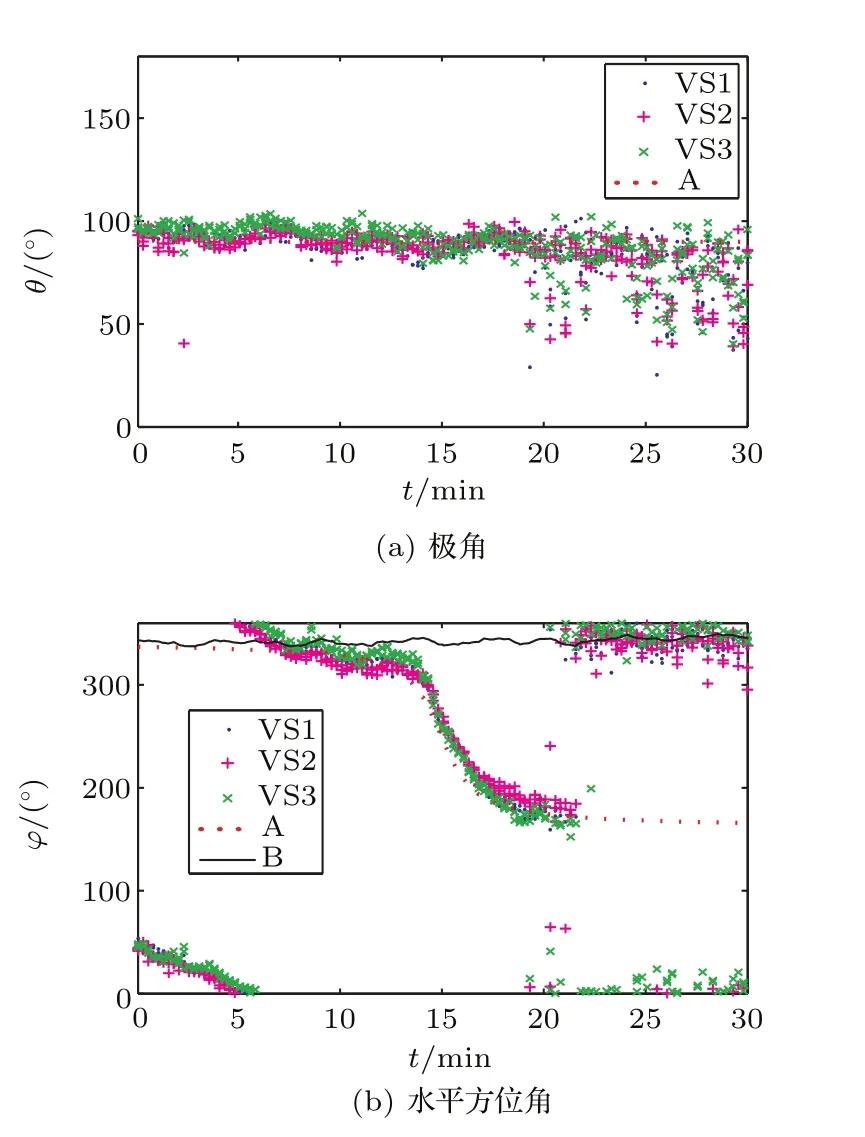
圖14　復聲強器方位估計方法按準則1獲得的VS1—VS3的極角和水平方位角Fig.14 Time course of azimuth by complex acoustic intensity method of VS1—VS3 according to criterion 1

3.4誤差分析

根據表達式（12）得圖15所示，VS1用平均聲強器和復聲強器方位估計方法按準則1的估計誤差。圖15中平均聲強器用黑點表示，復聲強器用紅色十字表示，橫軸時間段取8～22 min。

圖15（a）兩種方法在8～17 min期間的極角估計誤差變化趨勢基本相同，復聲強方法誤差主要分布在0值上下，而平均聲強器估值方法誤差偏向負值方向。在17～20 min，復聲強法的誤差還有明顯的趨勢，而平均聲強法已經開始發散。圖15（b）兩種方法的水平方位角誤差在8～16.5 min基本吻合，在8～12 min誤差在0°上下波動，而在14～16 min，目標船通過正橫方向時，誤差都增至10°～20°。在16.5～21.5 min，兩種方法有明顯的不同，復聲強方法誤差逐漸趨于0，而平均聲強器誤差變大。平均聲強器方法前后誤差分布區別較大，說明前面誤差較小可能是受漁船噪聲影響，后面誤差較大是受一直存在的本艦噪聲影響。在12～18 min內誤差情況基本相同，因此取12～18 min的誤差作為平均聲強器的誤差。

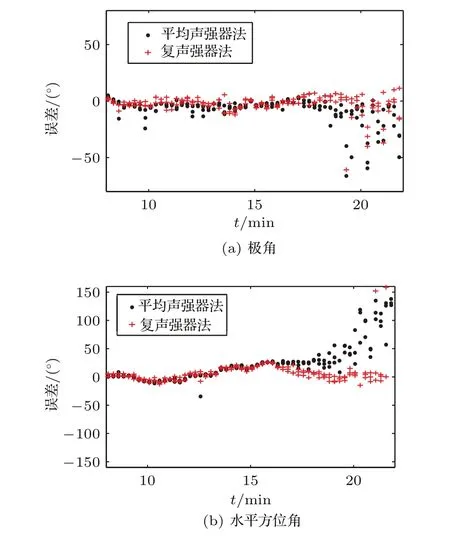
圖15　VS1用平均聲強器和復聲強器方位估計方法按準則1的估計誤差Fig.15　Estimation error of VS1 by azimuth by acoustic intensity averager and complex acoustic intensity method according to criterion 1

復聲強器在21.5 min之前誤差較小，為降低漁船的影響，時間段的起點設為12 min。因此取12～21.5 min的誤差情況作為復聲強器方法的誤差。

根據表達式（13）得平均聲強器和復聲強器方法在4個時間段的方位估計均方根誤差如表1所示。為降低漁船的影響，時間段的起點設為12 min。在求解時需要剔除個別極值點（取極角誤差范圍±80°內，水平方位角±160°內的誤差數據）。從表1可以看出，平均聲強器法極角和水平方位角估計誤差隨統計時間長度增加而增大。復聲強法極角估計誤差基本不變，約為8°；水平方位角估計誤差在13°上下變化，在12～18 min時間段統計的水平方位角誤差最大，因為此期間估計的水平方位角均偏離GPS實測值。

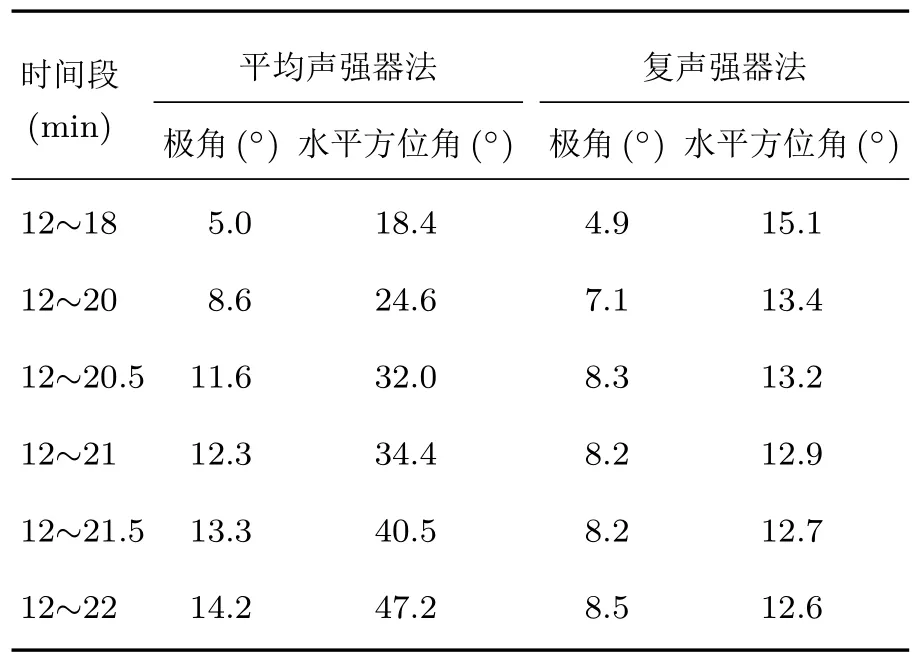
表1　平均聲強器和復聲強器方法在不同時間段估計目標方向的誤差Table 1　Error by acoustic intensity averagerand　complex　acousticintensity method during different time quantum

取12～18 min的估計誤差作為平均聲強器的誤差，水平方位角估計誤差為18°左右，極角估計誤差為5°左右。取12～21.5 min的估計誤差情況作為復聲強器方法的估計誤差，復聲強方法估計的水平方位角估計誤差為13°左右，極角估計誤差為8°左右。

4　討論

下面對兩種方法進行討論。

首先分析平均聲強器方位估計方法和復聲強器方位估計方法采用準則1的目標方位估計性能。

（1）采用準則1的復聲強器方位估計方法比平均聲強器法更準確。圖12（b）中VS1估計的方位角在21.5 min處“斷開”，將目標船A和接收船B的水平方位角分開。且17～22 min與目標船A很好地吻合。圖8（b）中目標船A過了正橫方向后，平均聲強器方法估計的水平方位角逐漸偏離目標船A，偏向接收船B的水平方位角方向。平均聲強器方位估計方法出現問題是由于其估計機制引起的。該方法的缺陷是不能有效分辨多個目標，其方位估值是幾個目標綜合的結果。隨著目標船遠離正橫方向，目標船輻射噪聲減弱，逐漸受到水聽器旁的接收船影響，使其方位值發生改變，但又不是其中一者的正確方位，從某種程度上說，應當是兩者的方向加權，權值是艦船噪聲強度。復聲強器方法選取的分析頻帶600 Hz～2000 Hz是目標船主要的輻射噪聲頻段，在目標船航行通過水聽器時，復聲強器方位估計方法針對目標船輻射噪聲的頻段進行估計，因此復聲強器方位估計方法估計要更準確。

（2）采用準則1的復聲強器方位估計方法比平均聲強器方法估計目標船的有效距離更遠。平均聲強器方位估計方法可以在12～18 min時間段確定目標船的方位，根據圖4地理坐標系下OA的水平方位角和距離，得平均聲強器方位估計方法最遠可以估計1.17 km處的目標船，而復聲強器方位估計方法正確估計目標船方位的時間段為8.5～21.5 min，則最遠可以估計2.35 km處的目標船。

再分析兩種方法采用準則2的相關問題。

（1）概率密度頻數分布時間歷程圖的線形粗細對準則1估值影響較小，對準則2影響較大。如圖7和圖11，兩種方法在艦船噪聲方向的概率密度頻數都顯著高于其它方向。平均聲強器方位估計方法在目標方向較尖銳，而復聲強器方位估計方法在目標方向±10°范圍內分布。這主要是由于進行直方圖估計的樣本數目不同造成的。在相同的T4=0.25 s時間段進行一次直方圖估計，平均聲強器方位估計方法的樣本數只有50個，遠小于復聲強器方位估計方法的樣本數3600個，樣本數的顯著差異影響了線形粗細程度。準則一只取最大值對應的角度，樣本數的多少并不影響概率密度的分布，因此線形粗細對該準則影響較小。而對于準則2，取的是期望值，即加權平均，當角度從0°跨至360°時，加權平均的結果受到的影響較大。

（2）準則2易出現估計錯誤。體現在兩種情況：（a）目標角度從0°變至360°時，采用兩種方法均估計出錯誤的結果，復聲強器方法比平均聲強器方法更為嚴重，這是由于復聲強器方法的樣本數較大，線形較粗，完全跨越0°需要的時間較長;（b）圖11（b）估計結果在360°附近時，采用準則2估計結果如圖13（b）所示，在180°左右，估計錯誤。

5　結論

本文提出采用概率密度值最大的方位角作為估值的方位估計準則，給出了平均聲強器和復聲強器方位估計方法在該準則下的估計誤差，并與采用方位的期望值的估計準則進行對比。海上實驗結果表明，矢量水聽器布放深度10 m時，對正橫距離0.42 km、航速10 kn的目標船，復聲強器方位估計方法可以對最遠2.35 km的目標船估計其方位，達到國外公開報道的水平［1］。在有接收船噪聲干擾情況下，矢量水聽器對目標船進行方位估計時，平均聲強器估計的水平方位角是目標船和接收船角度相互作用的結果。當目標船艦船噪聲減弱時，平均聲強器估計的角度逐漸偏向接收船的水平方位角，此時所估計的水平方位角方向上并不存在噪聲源，一次估計結果并不正確。復聲強器有效將目標船和接收船水平方位角分開，估計的結果只是其中之一。在建立海上分布式智能系統的輕型節點或移動節點時，采用復聲強器方法比采用平均聲強器方法估計的方位更準確，可對更遠處的噪聲源進行方位估計。

［1］FELISBERTO P，SANTOS P，JESUS S M.Tracking source azimuth using a single vector sensor［C］.2010 Fourth International Conference on Sensor Technologies and Applications，2010：416-421.

［2］SHIPPS J C，DENG K.A miniature vector sensor for line array applications［C］.IEEE Oceans Proceeding，2003：2367-2370.

［3］惠俊英，劉宏，余華兵，等.聲壓振速聯合信息處理及其物理基礎初探［J］.聲學學報，2000，25（4）：303-307. HUI Junying，LIU Hong，YU Huabing，et al.Study on the physical basis of pressure and particle velocity combined processing［J］.Acta Acustica，2000，25（4）：303-307.

［4］惠俊英，惠娟.矢量聲信號處理基礎［M］.北京：國防工業出版社，2009.

［5］姚直象，惠俊英，蔡平，等.單矢量水聽器方位估計的柱狀圖方法［J］.應用聲學，2006，25（3）：161-167. YAO Zhixiang，HUI Junying，CAI Ping，et al.A histogram approach of the azimuth angle estimation using a single vector hydrophone［J］.Applied Acoustics，2006，25（3）：161-167.

［6］ABRAHAM B M.Ambient noise measurements with vector acoustic hydrophones［C］.In Proc.of the OCEANS'06 Conf.Boston（USA）：MTS/IEEE，2006.

［7］休羅夫.海洋矢量聲學［M］.賈志富，譯.北京：國防工業出版社，2011.

［8］陳宇中.開環光纖陀螺性能改進及其在光纖矢量水聽器姿態測量上的應用研究［D］.長沙：國防科學技術大學，2011.

An experiment on azimuth estimation of target by single vector hydrophone

DA LianglongHOU WenshuSUN QindongWANG Wenlong
（Navy Submarine Academy，Qingdao 266071，China）

The capability of azimuth estimation with a combined co-vibrating vector hydrophone was tested in Yellow Sea.The vector hydrophone was dipped by the receiving vessel to estimate the azimuth of the target vessel which sailing uniformly in a straight line.The azimuth estimation methods are based on acoustic intensity averager and complex acoustic intensity method.Using the azimuth with maximum probability density as the azimuth estimate valuation criteria，the error of estimated azimuth based on these two methods is calculated. The vector hydrophone is dipped 10 m under water.With the noise of the receiving vessel，the estimated error of horizontal angle and polar angle based on acoustic intensity averager are 18 and 5 degree，respectively，and the maximum distance of azimuth estimation is 1.17 km，the estimated error of horizontal angle and polar angle based on complex acoustic intensity method are 13 and 8 degree，respectively，and the maximum distance of azimuth estimation is 2.35 km.In the case of the receiving vessel noise interference，the complex acoustic intensity method is stronger than the acoustic intensity averager.

Azimuth estimation，Acoustic vector hydrophone，Acoustic intensity average，Complex acoustic intensity

TB566

A

1000-310X（2015）06-0516-10

10.11684/j.issn.1000-310X.2015.06.007

2015-03-31收稿;2015-07-30定稿

?國家自然科學基金項目（61203271）

笪良龍（1967-），男，安徽桐城人，教授，博士生導師，研究方向：水聲工程。

E-mail：houwenshuc@163.com