無線傳感器網絡覆蓋空洞修復策略

曾雅麗 趙福雙

無線傳感器網絡覆蓋空洞修復策略

曾雅麗 趙福雙

隨著通信技術的發展，傳感器網絡給人們帶來了越來越多的便利。當傳感器網絡中隨意一個節點因它自帶的電能消耗盡或者監測的目標區域環境被破壞而失去通信功能，可能導致網絡出現覆蓋空洞而無法通信。覆蓋空洞會使鄰居節點能耗速度加快而死亡，使得無線傳感器網絡的覆蓋質量和通信效果變得不好，只有采用有效方案修復覆蓋空洞或對網絡重新部署，才能提高網絡資源利用和延長網絡使用時間。

無線傳感器網絡是由大量傳感器節點構成的無線網絡，其構成方式是以自組織和多跳的方式，其任務為在網絡覆蓋區域中的收集到的數據信息發送給數據使用者就是終端用戶如圖1。傳感器網絡節點操控的數據在行經其他節點逐跳傳達，在傳達的過程中數據或許會被節點處理過，經過很多跳到匯聚節點最后通過互聯網或移動通信網絡到達具有管理功能的節點，終端用戶用管理節點就可以操控網絡，全程的關鍵問題是對目標監測區域實現覆蓋。

移動傳感器網絡是由在需要采集信息的地方散開的可以移動的節點構成，可以根據節點準確的感知條件以及其通信功能實現節點的動態分布。與傳統的靜態傳感器網絡相比，擁有移動能力的傳感器網絡有覆蓋面積更大、對數據的反應速度快、獲取信息可靠性較高等特點。現在靜態的傳感器網絡有很多不足，例如獲取信息的能力不強、對巨大的數據不能進行處理、無法快速勘測目標監測區域環境特征等等。

研究及發展概況

圖1　無線傳感器網絡圖

傳感器節點在能量耗盡時可能會導致網絡產生覆蓋空洞。覆蓋空洞的存在會使空洞邊緣節點的能量消耗增加，節點死亡的速度增加，導致網絡覆蓋質量下降以及節點之間連通性降低，這樣一來整個網絡都會失去通信功能不能傳輸信息了，但仍然還有大很多節點沒有被使用到。

在大部分靜態傳感器網絡中使需要采集信息的地方每個節點對象都被k（k≥1）個節點覆蓋，多重覆蓋使得許多節點在能量消耗結束不起作用后，網絡仍然能保證需要采集信息地區的網絡密度，這樣的話在惡劣的條件下傳感器網絡能提高它的生命力。但是很多節點在同一時間都作用一個目標節點這會浪費節點的數量浪費成本。文獻選擇了空洞邊緣節點數目很多的冗余節點進行激活來修復覆蓋空洞，但該算法在一方面沒有周全考慮冗余節點的利用效率，另一方面忽略了多重覆蓋會形成很多經濟損失。

移動節點用時最少算法

算法概述

針對覆蓋空洞可以采取移動冗余節點進行修復，但移動的過程中會有能量的消耗，怎樣移動才能達到減少能耗又能修復空洞的目的？結合最小生成樹的思想提出了用時最少的算法，該算法的中心思想是當探測到無線傳感器網絡中存在覆蓋空洞，選取一個空洞邊緣節點作為移動節點，移動一個邊緣節點到空洞范圍內的網絡節點位置上，采取激活它能獲取信息的范圍距離內位置信息最好的冗余節點進行修復覆蓋空洞。

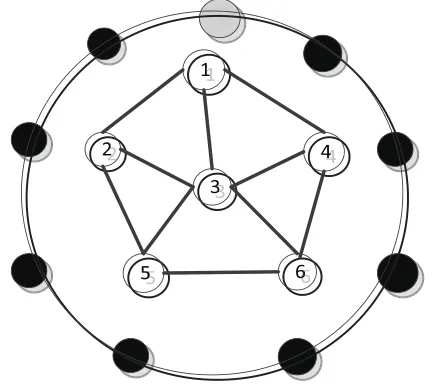
圖2　閉合空洞圖

問題描述

主要考慮已經探測到無線傳感器網絡中覆蓋空洞大小及位置信息情況下，怎么喚醒冗余節點進行覆蓋空洞修復。在圖2，節A-H以及節點M都是空洞邊緣節點，相互鄰接成閉合空洞區域，圖中紅色節點M為可移動節點，利用可移動節點行經空洞中喚醒其通信范圍內的冗余節點，根據可移動節點M的行走的路徑可以隨機選擇則可產生最優的路徑，使得其修復時間最短。

存在如下兩種情況如圖3。

1.當移動節點M移動到覆蓋空洞中網絡節點位置時，冗余節點在其通信范圍內，則可將其喚醒。

2.當移動節點M移動到覆蓋空洞中網絡節點位置時，冗余節點不在其通信范圍內，即冗余節點在其通信范圍以外，在這樣的情況下查找其附近具有通信功能的冗余節點，計算出移動節點與能通信的冗余節點之間的距離選擇合適的位置重新部署一個具有通信功能的節點，使得兩網絡節點間能相互通信。如圖4，移動節點M移動到節點1的位置，冗余節點2不在其通信范圍內，節點3為其附近具有通信功能的節點，節點N是節點1與節點3距離之間選取的合適位置，部署的新節點N的通信半徑為R，達到喚醒節點3且使得網絡能夠相互通信的目的。圓1與圓3與圓N的交點分別為a，b。

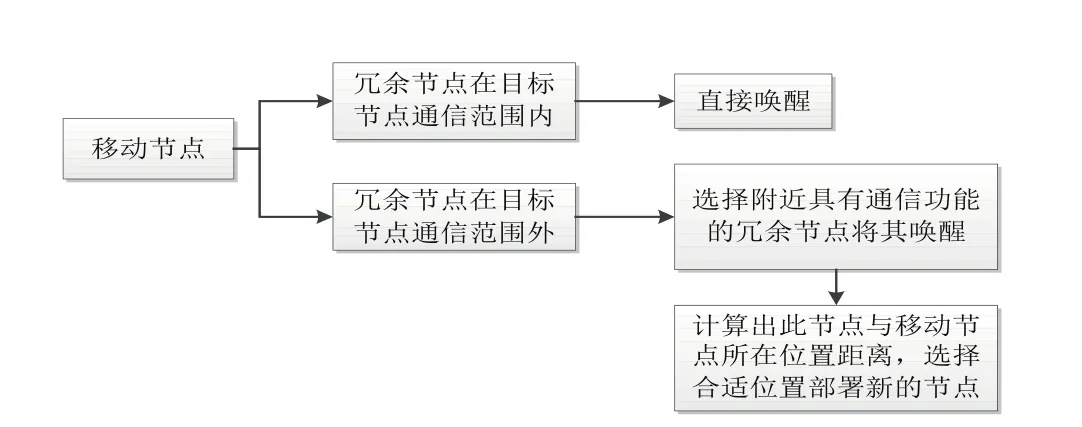
圖3　移動節點分類圖

圖4　喚醒節點圖

圖5　Kruskal算法步驟圖

算法描述

（1）最小生成樹Kruskal算法過程如圖5。

（2）最小生成樹Prim算法過程如圖6。

實驗驗證算法的優勢

我們分別對三種算法進行對比：最小生成樹Kruskal算法，最小生成樹Prim算法以及普通移動節點算法。對比結果如表1。

圖6　Prim算法步驟圖

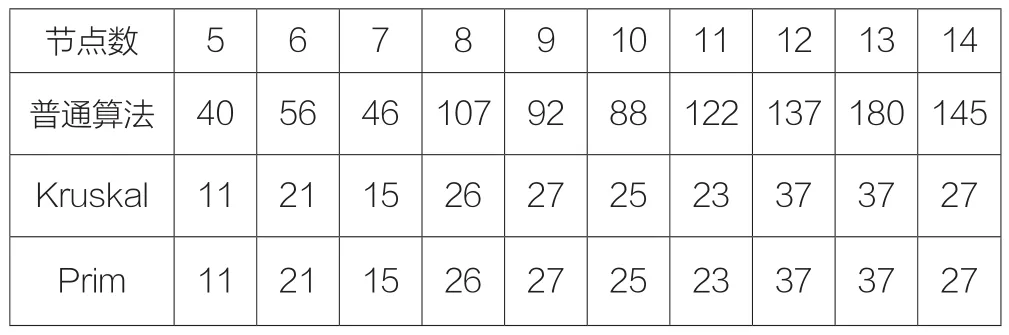
表1　三種算法權重值圖

如表1隨著隨機產生節點數的不同，采用Kruskal，Prim兩種算法所得權重相等也就意味著采用兩種進行修復所移動的距離是相同的，但都比普通算法所移動的距離少，即達到減少移動節點移動的距離來節約能量進行修復空洞的目標。在此過程中需要考慮時間因素，因為在移動相同距離，速度相同的情況下，只有時間最少的才能決定哪個算法更優，因為節點在移動的過程中會消耗能量，移動的時間越少能量消耗越少，使用減少時間達到更優修復空洞的目的。分析兩種的時間復雜度可知，Prim算法的時間復雜度為O（n2），Kruskal算法的時間復雜度為O（eloge）（e為邊的數量），綜合來說Kruskal算法比較適合邊數較少的時候，Prim算法比較適合邊數較多的時候，也就是說在節點較多時最佳選擇是Prim算法。

結束語

針對覆蓋空洞問題提出移動節點喚醒冗余節點的方法來進行修復，采用兩種算法進行對比，在不同情況下采取最優的方法進行修復。

10.3969/j.issn.1001-8972.2015.09.021