分支理論研究修正耦合KdV方程的行波解

饒 柯 李 熠

分支理論研究修正耦合KdV方程的行波解

饒 柯 李 熠

現代科學中有許多非線性現象，例如流體力學中的非線性波動，海洋中的突發海嘯，這些現象大多可以借助非線性發展方程來很好的描述。1895年荷蘭數學家克特韋格和德弗里斯從流力學的研究建立了描述淺水波的模型——KdV方程。為了更好的描述水波的運動過程，在本章中我們將研究耦合KdV方程，可以描述分層流體內部波之間的近共振相互作用，我們將利用分支理論的方法給出其常微分系統的形式，畫出軌線圖，分析解的類型，得到耦合KdV方程的解析解。

修正的耦合KdV方程

在淺水波模型中水波的傳播一般由KdV方程來描述，但是在某些特定物理條件下，如在不同的水波分層中，其引起的雙折射會使得水波的偏振量出現不同的群速度從而可能導致水波的展寬甚至分裂，因此如何描述這種分層流體內部之間的近共振相互作用，如何找到一種較好的解決方式，這都是我們要考慮的問題。在這種情況下，研究模型就變為耦合KdV方程，它在研究水波內部分層之間相互作用方面有著重要的應用。目前已經有很多文獻研究了耦合KdV方程的解析解。1981年，Hirota提出下列耦合KdV方程用來描述水波之間的相互作用

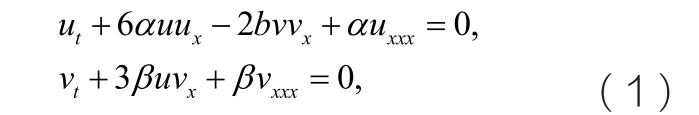
這里α、β和b都是常數。Liu運用奇次平衡法，給定一個特定的表達式，借助符號運算，得到一系列的周期解和孤子解。在本章中，我們將考慮一個如下形式的耦合KdV方程

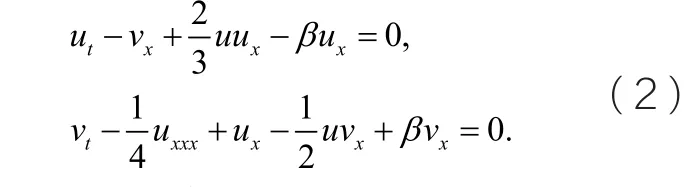
其中u 和v 分別是表示空間變量x 和時間變量t的函數，β是實數。通過分支理論的方法和定性分析，我們得到了新的解析解，包括尖端解，孤子解和橢圓函數周期解，同時得到新的拓展的橢圓函數解。

本文內容安排如下：我們首先給出方程（2）的常微分系統形式，并通過分支理論的方法得到六組不同的方程的軌線圖。得到了同宿軌、異宿軌和周期閉軌，基于軌線圖，我們將求解出方程解的具體形式。

耦合KdV方程的解析解

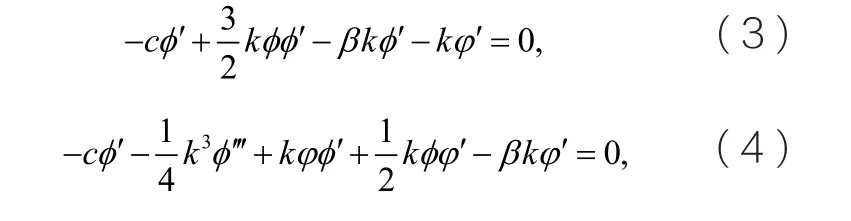
關于ξ對方程（4）積分一次，我們得到

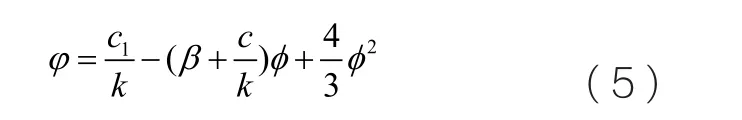
這里c1是積分常數。

然后將（5）式代入（4）式，并且關于ξ積分一次，我們得到

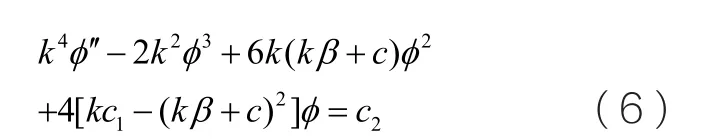
通過合適的參數變換，可以把積分常數c2化簡。

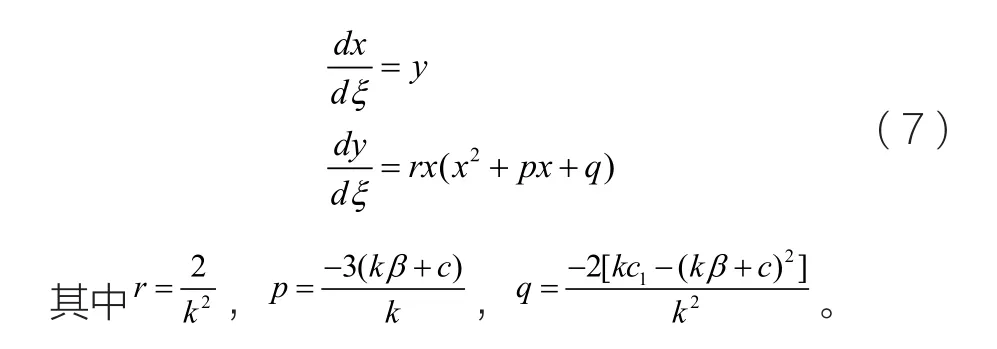
對系統經行首次積分我們得到

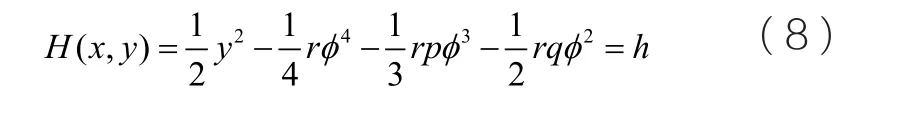
這里h是積分常數。現在我們討論系統（7）的軌線圖。

令M（ x0，y0）是系統（7）在平衡

點（x0，y0）和J（ x0，y0）近似矩陣的雅克比系數矩陣。顯然，在（x， y）平面上，系統（7）的平衡點的橫坐標的零解方程是設）是系統（7）的平衡點之一。從平面系統的分支理論我們可以得到，如果J（ x?，0）＞0，那么平衡點（x?，0）可以判別為中心點；如果J（ x?，0）＜0，那么平衡點（x?，0）的類型為鞍點。根據以上的判斷，我們可以得到系統（7）的以下結論：

（1）如果q2＞4q ，p≠0且q＜0，如圖一所示，平面系統（7）有兩個鞍點和一個中心點系統存在兩條異宿軌鏈接著兩個鞍點，和一個周期閉軌圍繞著中心點（0，0），通過軌線圖我們可以知道方程（2）有一組扭結型或者是反扭結型的孤子解和一組橢圓函數周期解。

（2）如果q2＞4q ，p=0且q＜0，如圖2所示，我們可以得到系統（7）有兩個鞍（±-q，0）點和一個中心點（0，0）。通過軌線圖我們可以知道這就意味著方程（2）存在著一組扭結型或者是反扭結型的孤子解和一組橢圓函數周期解。

（3）如果q2＞4q 且q＞0，如圖3所示，系統（7）存在兩個中心點）和一個鞍點（0，0）。系統存在兩條同宿軌連接著鞍點O（0，0），和兩條周期閉軌圍繞著兩個中心點，通過軌線圖我們可以知道這就代表方程（2）存在兩組沖擊波類型的孤子解和三組橢圓函數周期解。

（4）如果q2＞4q 且q=0，如圖4所示，系統（7）只有兩個平衡點O（0，0）和通過分支理論和定性分析我們可以得到點O 和點P分別是鞍點和結點。這就意味著方程存在著沖擊波類型的孤子解和扭結型的孤子解。

（5） 如果q2=4q，如圖5所示，系統（7）有兩個平衡點O（0，0）和通過分支理論和定性分析我們可以得到點P 和點O分別是鞍點和結點。同上一個情況一樣，意味著方程存在著沖擊波類型的孤子解和扭結型的孤子解。

（6） 如果q2＜4q，如圖6所示，系統（7）只有一個平衡點O（0，0），通過軌線圖我們可以知道這代表方程只存在一組孤子解。

接下來，我們將會根據上述討論的結果，通過平面系統（7）的首次積分和橢圓函數方法來求得方程（2）的解析解。

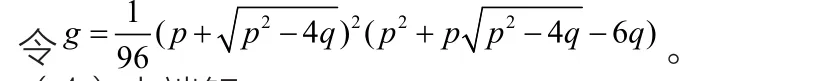
（1）尖端解

當h=0，p2＞4q 且q=0時，我們可以從圖4中看到，軌線圖中存在一個異宿軌連接著鞍

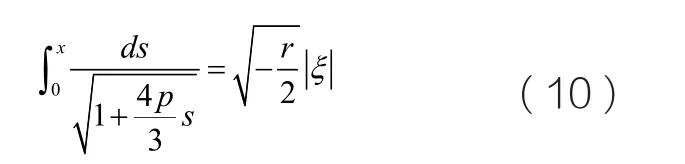
完全積分且對x進行求解，我們可以的到尖端解的表達式如下所示：

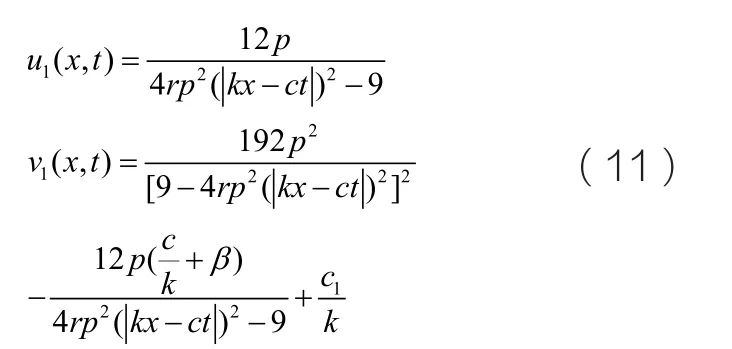
當h=0且p2=4q 時，我們從圖5中可以得知，同樣存在一條異宿軌連接著鞍點）和尖端點O（0，0）。那么在（x， y）平面上我們可以得到其表達式為：

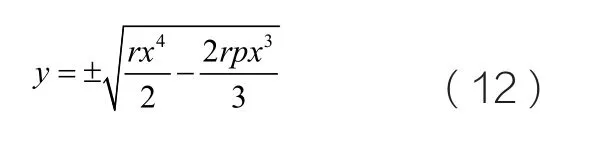
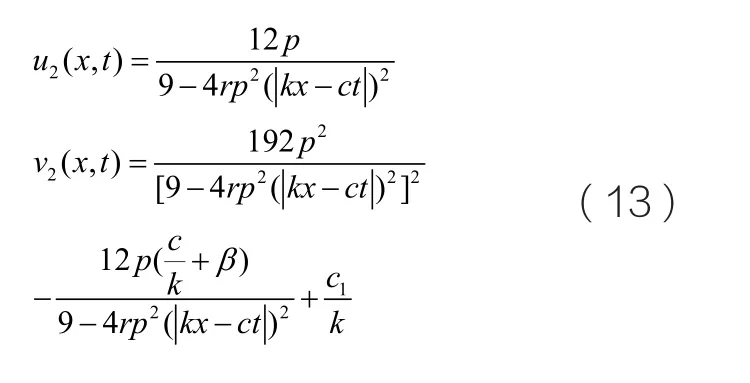
（2）沖擊波類型的孤子解

當h=g ，q2＞4q 且q＜0時，我們可以從圖一和圖二中得知，軌線圖上有兩條異宿軌連接著兩個鞍點和一組周期閉軌圍繞著中心點O（0，0）。那么在（x， y）平面上我們可以得到其表達式為：

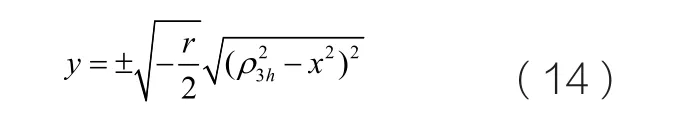
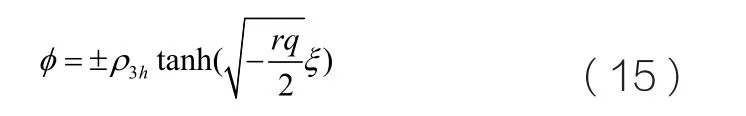
從而我們得到沖擊波類型的孤子解u（ x， y ）和v（ x， y）分別如下所示：

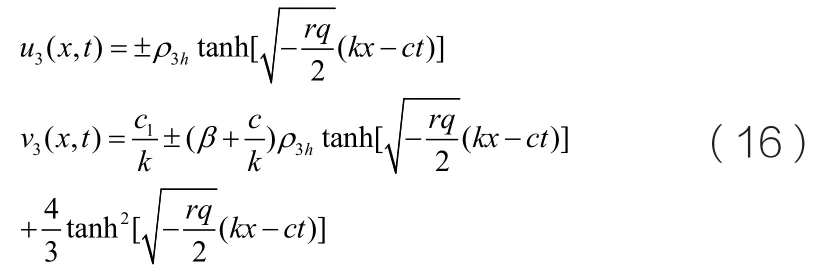
當h=0，q2＞4q 且q＞0時，我們可以從圖三中看到軌線圖中存在一組對稱的同宿軌線連接著鞍點O 。那么在（x， y）平面上我們可以得到同宿軌的表達式為：

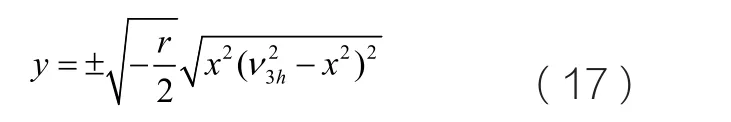
接著求得x 的表達式

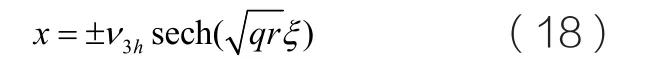
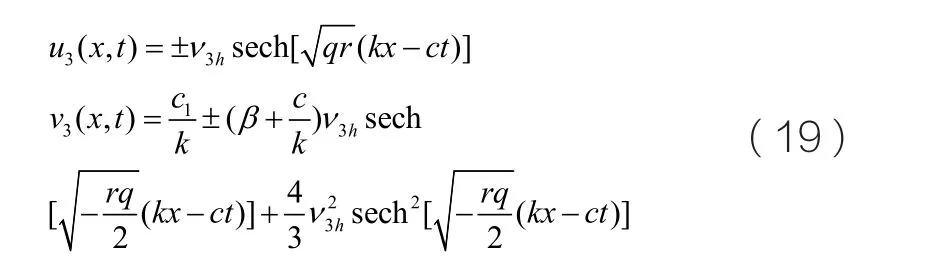
如圖4所示，當h=0、p2＜4q 且c2=0時，方程等價于：

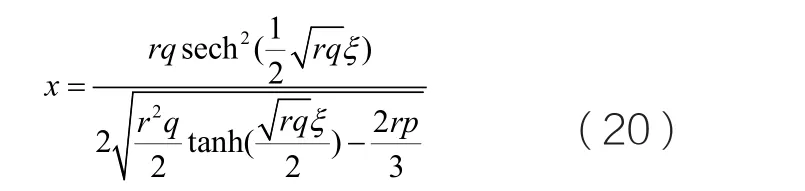
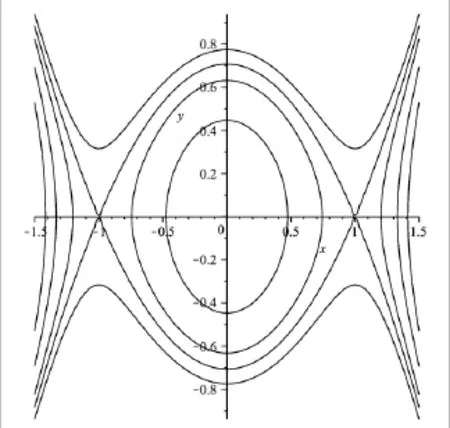
圖1　

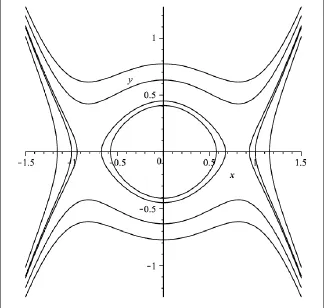
圖2　

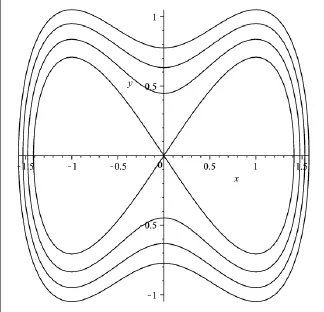
圖3　

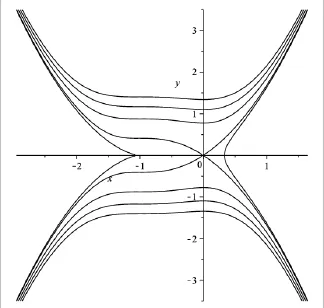
圖4　

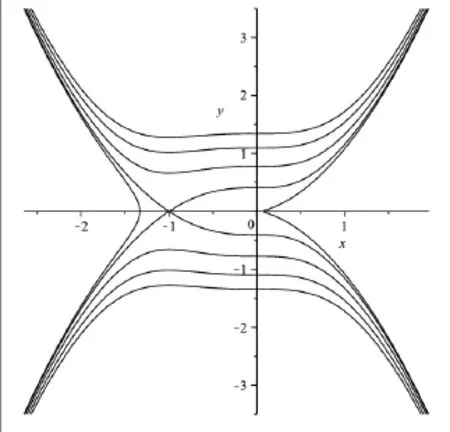
圖5　

圖6　

（3）橢圓函數周期解

當h∈（0，g ），我們從圖一中可以看到，系統（7）存在一組周期閉軌。那么在（x， y）平面上我們可以得到這組周期解的表達式為：

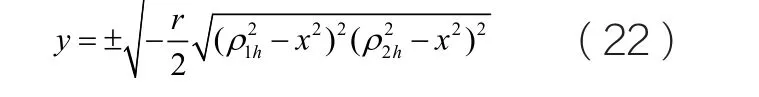
這里

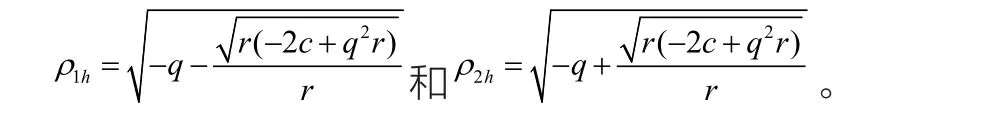
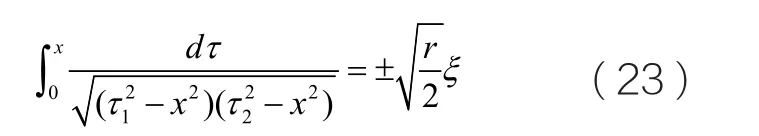
從（23）式中得

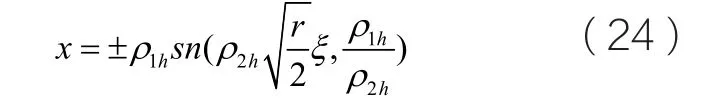
又因為x=x（ξ）和ξ=kx-ct，我們得到關于耦合KdV方程的一組周期解：

當h∈（-g ，0）時，我們從圖三中可以看到軌線圖中系統（7）的同宿軌中存在著兩組周期

的閉軌。那么在（x， y）平面上我們可以得到這組閉軌的表達式為：

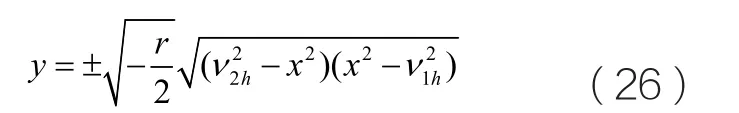
這里ν1h和ν2h和由上式所給出的ρ1h和ρ2h一樣。

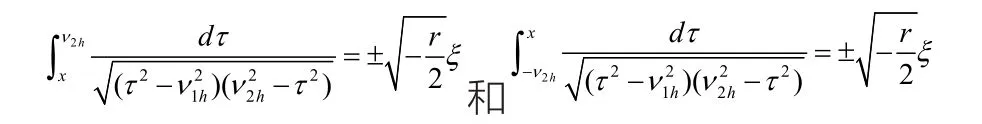
由上式我們可以得到

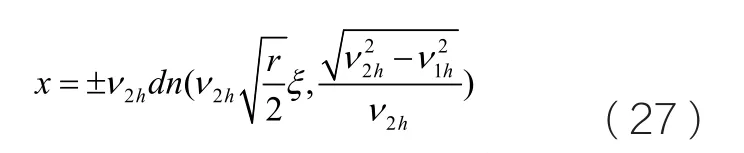
又因為x=x（ξ）和ξ=kx-ct ，我們得到一組周期解：

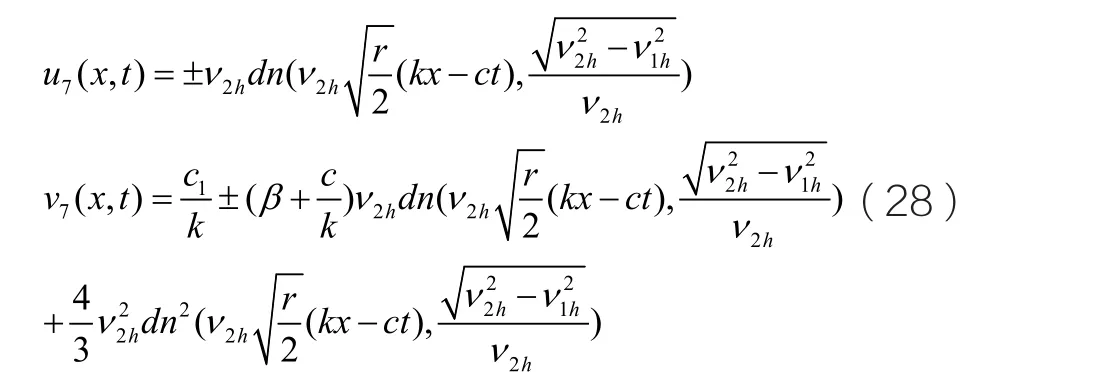
當h＞0時，我們從圖三可以看到在同宿軌線的最外層有一組閉合的周期軌線，那么

在（x， y）平面上我們可以得到這組周期解的表達式為：

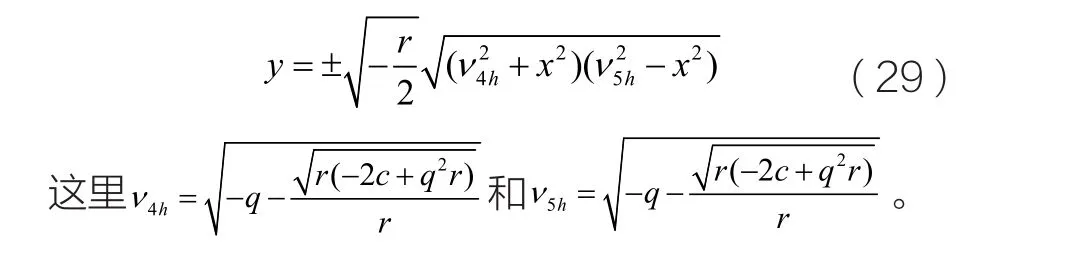
結合上式，我們得到

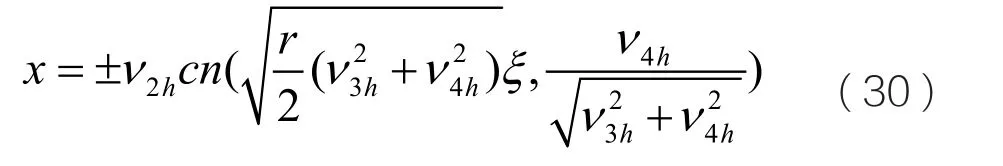
因此我們得到一組橢圓函數周期解

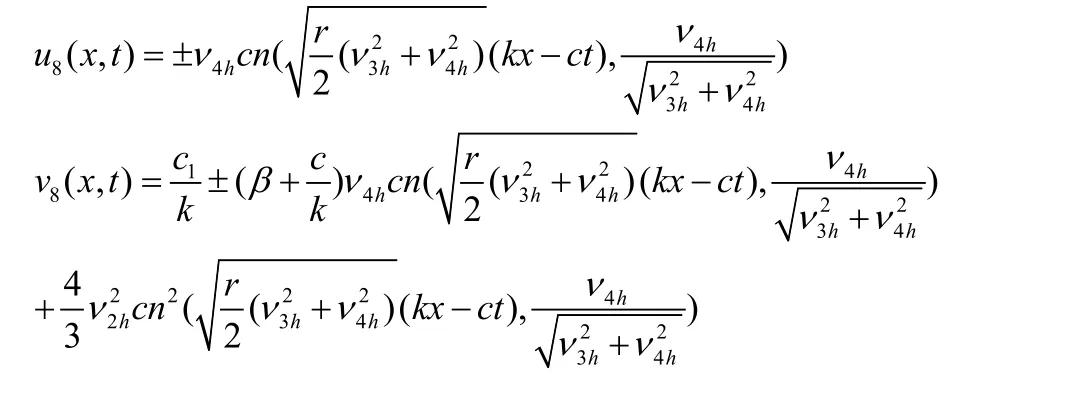
結束語

本文運用分支理論的方法和軌線圖對修正的耦合KdV方程進行討論。在不同的參數下，討論了六種情形的軌線圖，基于軌線圖的性質，運用橢圓函數展開的方法，我們得到了相應的解——尖端解、沖擊波解和周期解。

10.3969/j.issn.1001-8972.2015.15.001