空腔噪聲非線性數值模擬*
王一丁,陳濱琦,郭 亮,鐘范俊,童明波
空腔噪聲非線性數值模擬*
王一丁1,陳濱琦1,郭 亮2,鐘范俊2,童明波1
(1.南京航空航天大學 航空宇航學院, 江蘇 南京 210016; 2.成都飛機設計研究所, 四川 成都 610091)
將雷諾平均N-S方程與非線性噪聲求解方法相結合,對M219空腔在Ma=0.6,Ma=0.85,Ma=1.35條件下進行了氣動噪聲分析。通過雷諾平均N-S方程求解空腔流場,得到包含空腔平均流場基本特征以及強制設定的湍流脈動統計描述的初始湍流統計平均解,采用非線性噪聲求解方法重構噪聲源并高精度模擬壓力脈動的傳播。通過與試驗結果對比表明非線性噪聲求解方法能夠較好地捕捉空腔流動中的壓強脈動及噪聲水平。與分離渦模擬方法相比,非線性噪聲求解方法在保持計算精度的同時大大減少計算網格,對內埋彈艙快速設計具有一定的參考意義。
空腔;非線性;噪聲源;湍流;內埋彈艙
(1.CollegeofAerospaceEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China;
2.ChengduAircraftDesignandResearchInstitute,Chengdu610091,China)
空腔結構廣泛存在于飛行器中,新一代戰斗飛行器使用內埋彈艙能夠使飛行器的阻力最大降低30%,雷達橫截面最低可達0.07~0.12m2[1]。內埋彈艙給飛行器帶來了隱身、超聲速巡航等益處,但同時也產生了一系列復雜的空氣動力學問題,包括剪切層極不穩定、邊界層分離、激波邊界相互干擾等[2-3],這加劇了空腔內的非定常效應,由此產生的氣動噪聲將對飛行器的性能與安全產生影響,嚴重時將導致飛行器產生災難性的后果。因此對于空腔氣動噪聲的研究具有重大而緊迫的現實意義。
Le等[4]采用大渦模擬方法(LargeEddySimulation,LES)、Allen等[5]采用分離渦模擬(DetachedEddySimulation,DES)以及Peng等[6]采用混合雷諾平均大渦模擬(Reynolds-AveragedNavier-Stokes/LES,RANS/LES)對空腔噪聲進行了數值模擬研究。但對于工程實際問題,這些方法存在計算網格數量大、計算時間長等缺點。目前噪聲領域常用的DES方法經常與有限傳輸算法結合使用,增加了亞格子尺度模型的耗散,有可能導致有效粘度過大,同時統計學湍流能量的傳輸也存在很大困難,這極大地限制了DES方法適用的流動及網格類型。
Batten等于2002年提出了一種非線性噪聲求解(NonlinearAcousticSolver,NLAS)方法,該方法通過對湍流物理量進行重構兼顧了亞格子尺度聲源的影響,在保持計算精度的同時降低了網格需求[7-9]。王一丁等將NLAS方法引入內埋彈艙噪聲預測中,計算了英國QinetiQ公司M219空腔[10],空腔計算條件為Ma=0.6,Ma=0.85,Ma=1.35,將NLAS仿真結果與試驗數據以及Allen[5]使用DES方法計算結果進行了對比,驗證了NLAS方法用于空腔噪聲預測的有效性與準確性。NLAS方法計算網格數相對DES方法大幅減少,降低了計算成本,具有一定的工程應用價值。
1 數值方法
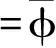
(1)
式中,
(2)
(3)

忽略密度脈動項,對以上方程取時間平均可得:
(5)
(6)
式中,Ri是標準雷諾應力張量和湍流熱通量相關項。求解噪聲的關鍵是通過RANS計算求得到這些未知項,不能求解的小尺度量則通過RANS計算得到的湍流統計結果重構出來,以此生成亞格子源項。Batten提出的湍流重構方法為:
(7)
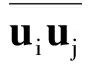
(8)
2 計算模型
2.1 腔體構型
M219模型為典型的開式空腔,在QinetiQ風洞進行了一系列風洞試驗,腔體長深比L/D=5,寬深比W/D=1.0。圖1為腔體在DERA風洞試驗的照片,圖2為M219空腔風洞試驗件構型圖。

圖1 M219空腔在DERA風洞噪聲試驗Fig.1 Noise test of M219 cavity in wind tunnel
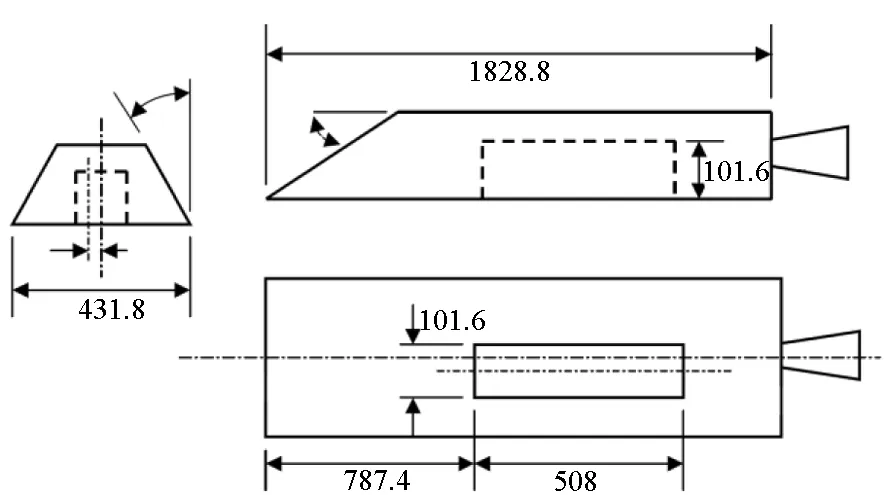
圖2 M219空腔風洞試驗件構型圖Fig.2 Sketch of M219 wind tunnel test pieces
2.2 計算網格
圖3為RANS計算網格區域,整個計算域由4個結構塊組成,來流方向(x)從-8D到12D,展向從-2D到2D,壁面法向方向從-1D到4D。為了更好地模擬湍流脈動的統計平均結果,RANS計算應采用非線性的各向異性湍流模型,選取cubick-epsilon模式,該模式通過矩陣近似各個位置對渦粘系數的影響,更加符合物理本質。流場物面第一層網格尺度為5×10-2mm,網格數量為260萬,基于空腔深度的雷諾數Re=7×106。RANS求解的超聲速時來流為固定超聲速來流入口條件,遠場為特征線條件,出口邊界不指定,由內層網格物理量推得。亞聲速時來流入口、遠場及出口位置均采用特征線邊界條件。
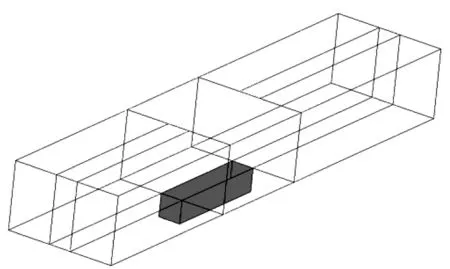
圖3 RANS計算區域Fig.3 Computational domain of RANS
噪聲計算采用單獨的計算網格,物面邊界為黏性無滑移絕熱壁,采用壁面函數法求解保證物面區域求解精度。RANS計算得到當地雷諾應力張量和熱通量的統計平均值,將它插值到噪聲計算網格,根據這一統計平均結果對湍流進行人工重構。NLAS方法的優勢在于噪聲求解器可以在各項同性更好的網格單元上進行計算,特別是在近壁面區域。在進行噪聲計算時,計算域選取為包含噪聲源周邊的區域。圖4為RANS計算得到的最大湍流動能kmax的10%等值面,這部分區域是湍流脈動最為劇烈區域、也是主要的噪聲源區域、噪聲網格重點關注區域。新的邊界被設置為吸收層邊界,它的遠場及衰減層數據由之前RANS計算提供。

圖4 RANS計算10% kmax等值面(背景為來流速度)Fig.4 Iso-surface of 10% kmax calculated by RANS(shaded with streamwise velocity)
由于近壁面網格要求放寬以及計算域的縮小,噪聲計算網格數量為120萬,較RANS計算的260萬網格有了顯著減少。RANS與NLAS計算的網格對比如圖5所示。
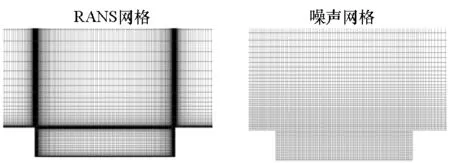
圖5 RANS網格與噪聲計算網格對比Fig. 5 Comparison of RANS and acoustics meshes
RANS計算控制方程采用有限體積法求解,無黏項采用二階精度TVD格式離散,黏性項采用中心差分格式離散,時間推進采用隱式方法。NLAS計算空間和時間離散格式與RANS計算相同,時間步長Δt=2×10-5s,共計算20 000步。
來流馬赫數與M219風洞試驗一致,取Ma=0.6,Ma=0.85,Ma=1.35,覆蓋了亞、跨、超聲速以充分驗證NLAS方法在各種來流條件下模擬空腔噪聲的有效性與準確性。在空腔底面中心線處設置10個點記錄壓力的變化,分別表示為K20~K29,具體位置如圖6所示。

圖6 脈動壓力監測點位置Fig.6 Monitoring locations of oscillating pressure
計算使用4個計算機節點,每個計算機節點包含1個8核2.6GHz處理器和24G內存。
3 計算結果對比分析
空腔底部監測點壓強均方根是測量脈動壓力的常用指標。圖7~9為Ma=0.6,Ma=0.85,Ma=1.35條件下由NLAS方法計算得到的壓強均方根值與QinetiQ風洞試驗值以及Allen等[5]采用DES方法計算的結果對比。

圖9 Ma=1.35壓強均方根試驗、DES及NLAS對比圖Fig.9 Comparison of prms between experiment, DES and NLAS at Ma=1.35
通過圖7~9可以看到NLAS計算得到的均方根值略大于試驗值,與DES方法計算值精度基本相當。而NLAS方法所用網格數量僅為120萬,DES方法所用網格數量為260萬,在保證計算精度的同時,NLAS方法大大減少了網格需求,縮短了計算時間。

x方向

y方向

z方向圖10 NLAS方法得到的渦量分量瞬時等值面Fig.10 Instantaneous streamwise vorticity iso-surfaces calculated by NLAS
圖10為空腔在Ma=0.85下x,y,z方向渦量瞬時等值面,渦量相同均為6×103,背景代表流向速度。
對于長深比L/H=5的開式空腔,來流氣體流經前緣時,因為腔體深度較大,氣流未觸及空腔底部,剪切層跨越空腔中部與后壁發生碰撞,空腔前部和中部受剪切層影響較小,壓力不會發生大的變化,空腔后部壓力上升,對于超音速流動,會誘發激波產生。空腔的流動特性以及腔內復雜的流動環境會導致空腔后部發生顫振,從而產生噪聲。噪聲通過腔內循環氣流傳播到空腔前緣,導致剪切層分離,當滿足一定相位條件時,形成聲波反饋循環,發生腔內自持振蕩。
圖11~13分別為Ma=0.6,Ma=0.85,Ma=1.35下,位于空腔底部中心線X/L=0.25,X/L=0.55,X/L=0.95三個監測點NLAS仿真得到的聲壓頻譜曲線與試驗值對比圖。由于壓力脈動值在計算起始的一段時間內不具有周期性,而在該段時間之后壓力脈動呈現出一定的周期特性并一直保持下去,而這正是所需要的壓力脈動數據,也是噪聲傳播對應的數據。為了防止起始時間的不規則壓力脈動影響噪聲求解,將起始段的壓力脈動截掉,使用0.1s~0.4s的脈動數據。
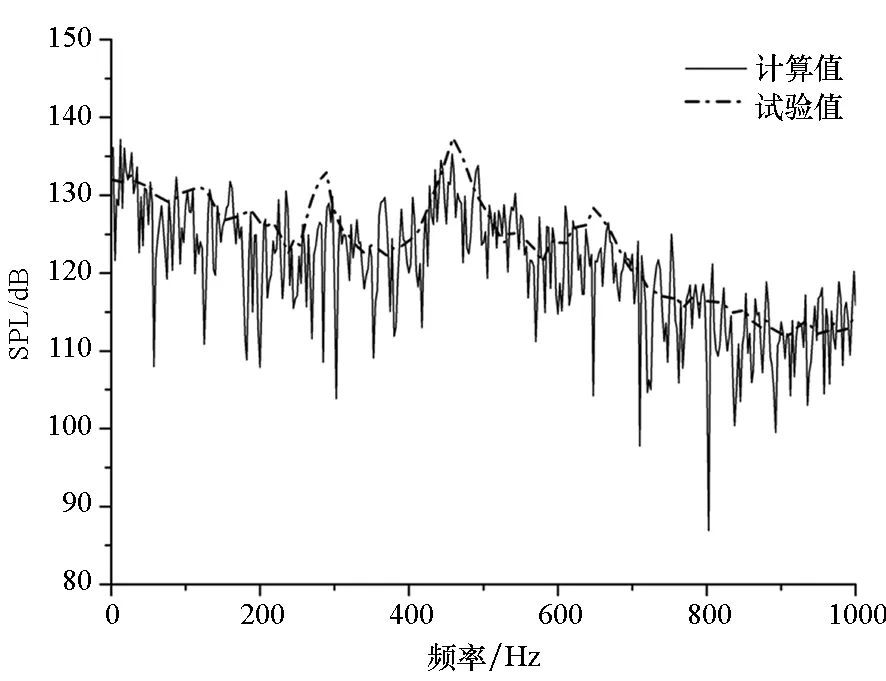
(a) K22(X/L=0.25)
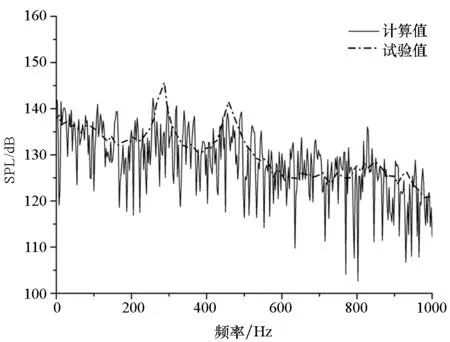
(b) K25(X/L=0.55)

(c) K29(X/L=0.95)圖11 Ma=0.6監測點聲壓頻譜特性計算與試驗對比Fig.11 Comparison of spectrum between calculation and test at Ma=0.6
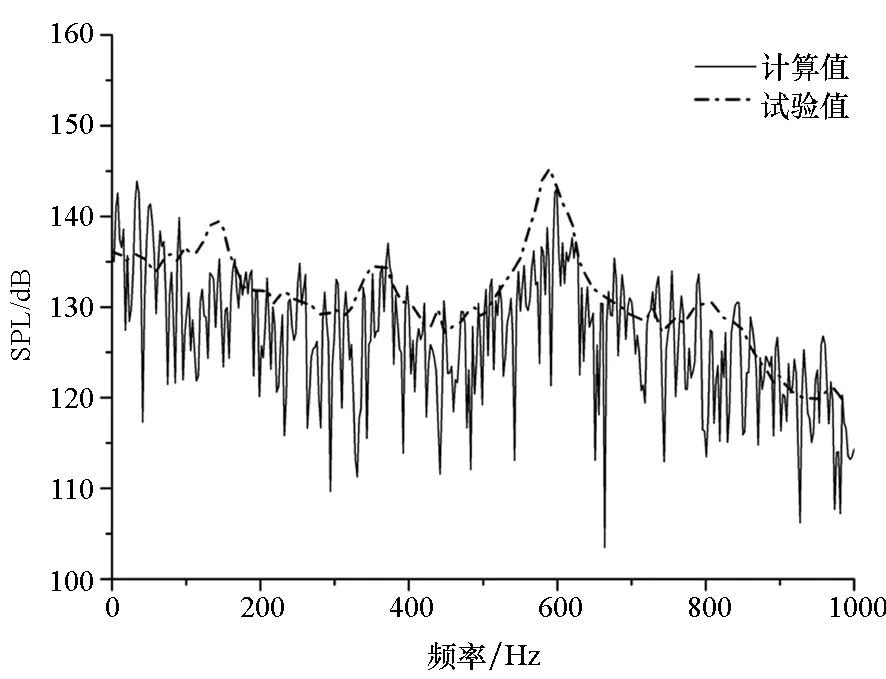
(a) K22(X/L=0.25)

(b) K25(X/L=0.55)
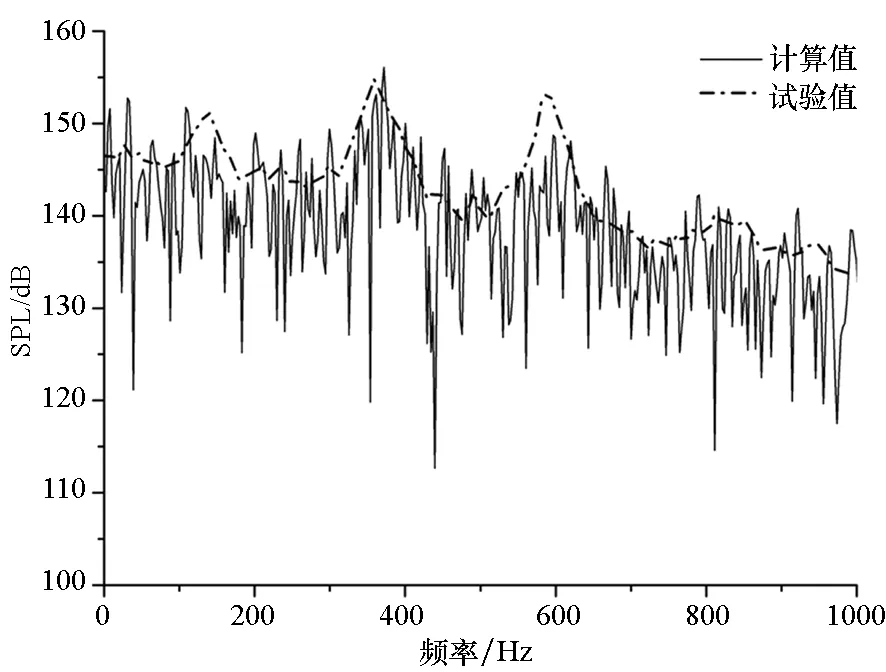
(c) K29(X/L=0.95)圖12 Ma=0.85監測點聲壓頻譜特性計算與試驗對比Fig.12 Comparison of spectrum between calculation and test at Ma=0.85
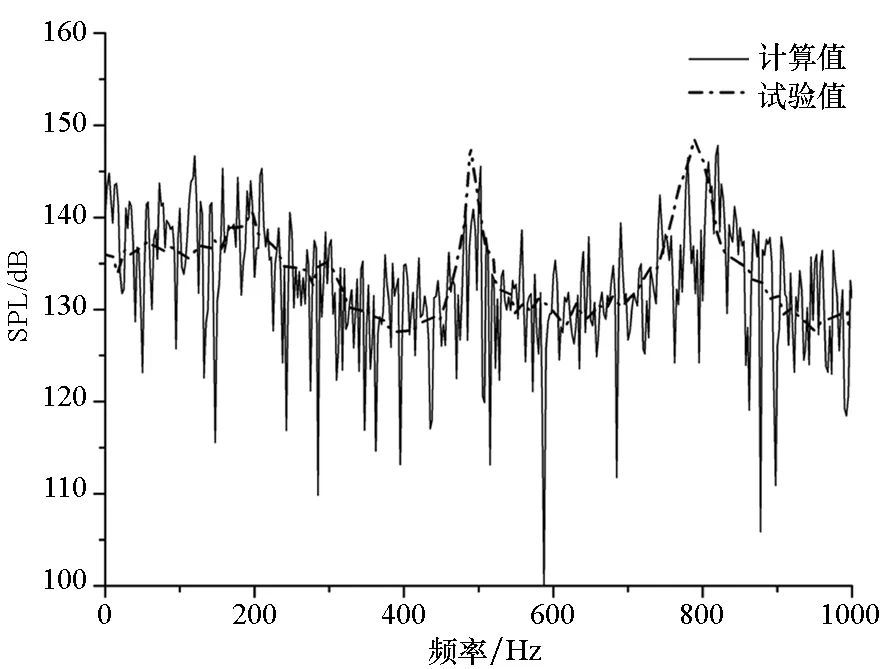
(a) K22(X/L=0.25)
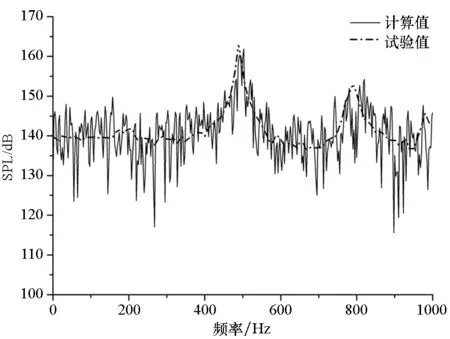
(b) K25(X/L=0.55)
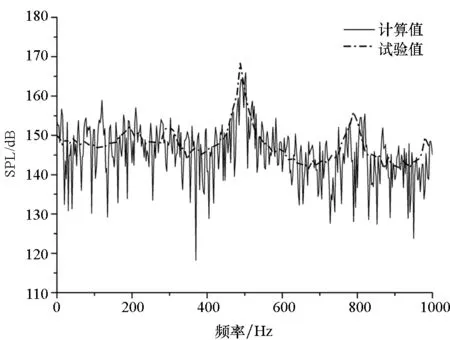
(c) K29(X/L=0.95)圖13 Ma=1.35監測點聲壓頻譜特性計算與試驗對比Fig.13 Comparison of spectrum between calculation and test at Ma=1.35
計算結果表明,不同馬赫數下不同位置的模態一致,這與文獻中給出的典型頻譜符合很好。從頻譜模態中可以看出,采用本方法進行氣動噪聲計算,前4階頻譜模態均可以被捕捉到,且除個別模態略有差別外,主頻均被精確捕捉到,說明本方法具有較高精度。Ma=1.35時,噪聲測點聲壓級分布集中在130~170dB之間,上游聲壓級略低,而下游聲壓級略高。對于類似結構的內埋彈艙而言,如此高的聲壓級會對艙體以及艙內武器造成疲勞損傷,且這種分布會使艙內武器生成一定的抬頭力矩,這主要是由于上游剪切層與下游壁面邊界層互相作用產生不穩定壓力波,該不穩定壓力波主要集中于下游區域,并且從下游沿壁面向上游傳播至上游前緣,再與剪切層互相作用使之與壁面分離從而形成聲學反饋。在空腔中主要的不穩定區域集中于下游,使得下游噪聲聲壓級明顯高于上游。
氣動噪聲計算中最重要是主頻位置及其對應的最高聲壓級的預測,重點對這兩個參數的仿真與試驗結果進行了對比。表1為Ma=0.6,Ma=0.85,Ma=1.35下空腔底部前中后三個位置的數值仿真結果與試驗結果中的最高聲壓級對比,表2為主頻對比。
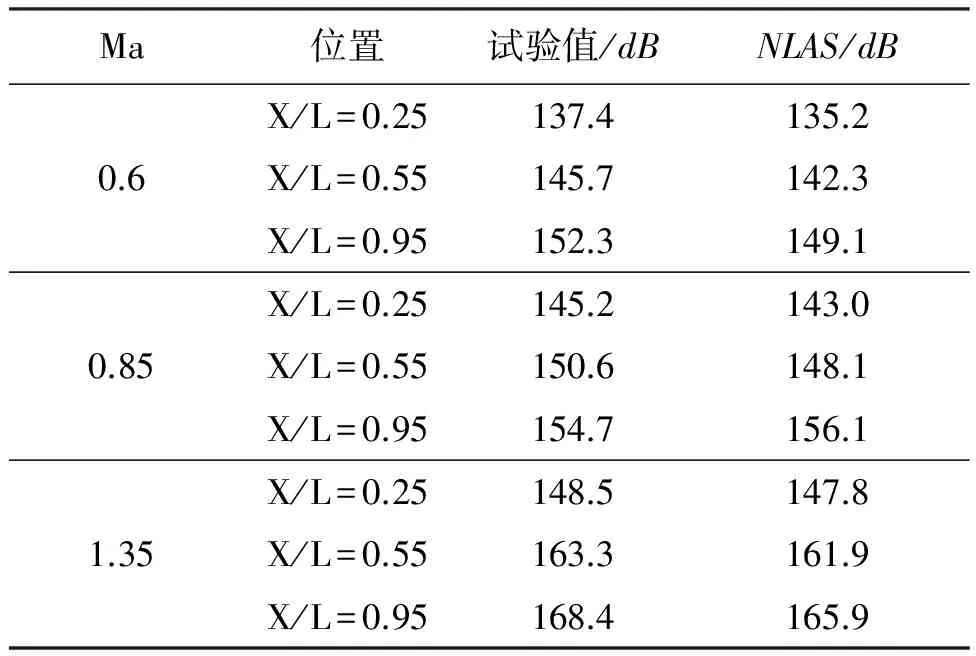
表1 最高聲壓級比較

表2 主頻位置比較
通過對比不同馬赫數下NLAS仿真與試驗的最高聲壓級以及主頻位置,可以發現NLAS方法能較為精確地模擬出亞、跨、超聲速情況下空腔噪聲主頻及其對應的最高聲壓級。
4 結論
1)將非線性噪聲求解方法NLAS應用于空腔噪聲預測,模擬了Ma=0.6,Ma=0.85,Ma=1.35三種來流條件下的空腔噪聲。應用cubick-ε湍流模型,遠場吸收邊界及壁面函數法計算得到了三種來流條件下空腔噪聲特性,數值結果與試驗結果基本吻合,特別是準確模擬主頻及其對應的最高聲壓級,表明NLAS方法在亞、跨、超聲速條件下對空腔噪聲有較好的預測能力。
2)非線性噪聲求解方法對于近壁面網格要求低,聲場計算域比RANS小,可減少噪聲計算網格數量,降低計算成本。將NLAS計算結果與國外文獻中DES計算結果進行對比,NLAS的計算精度與DES相當,但是網格數大大降低,因此NLAS方法對于內埋彈艙工程快速設計具有一定的意義。
3) 對于L/D=5的典型開式空腔,通過對亞、跨、超聲速情況下空腔噪聲數值計算與試驗對比,隨著馬赫數的增大,各監測點的噪聲主頻位置,總聲壓級都有所增大。
References)
[1]MicharelJH. 戰術導彈空氣動力學[M].洪金森,楊其德,毛國良,譯.北京:宇航出版社,1999.
MicharelJH.Tacticalmissileairdynamics[M].TranslatedbyHONGJinseng,YANGQide,MAOGuoliang.Beijing:AstronavigationPress, 1999. (inChinese)
[2]MurrayNE,UkeileyLS.Flowfielddynamicsinopencavityflows[C]//Proceedingsof12thAIAA/CEASAeroacousticsConference,AIAA2006-2428, 2006.
[3] 吳繼飛,羅新福,范召林.內埋式彈艙流場特性及武器分離特性改進措施[J].航空學報,2009,30(10):1840-1845.WUJifei,LUOXinfu,FANZhaolin.Flowcontrolmethodtoimprovecavityflowandstoreseparationcharacteristics[J].ActaAeronauticaetAstronauticaSinica,2009,30(10):1840-1845. (inChinese)
[4]LeTH,MaryI,TerracolM.LESofpressureloadssuppressioninweaponsbayflow[C]//Proceedingsof43rdAIAAAerospaceSciencesMeetingandExhibit,AIAA2005-794, 2005.
[5]AllenR,Mendon?aF.DESvalidationsofcavityacousticsoverthesubsonictosupersonicrange[C]//Proceedingsof10thAIAA/CEASAeroacousticsConference,AIAA2004-2862, 2004.
[6]PengSH,HaaseW.AdvancesinhybridRANS-LESmodelling,notesonnumericalfluidmechanicsandmultidisciplinarydesign[M].USA:Springer, 2008 : 132-141.[7]BattenP,RibaldoneE,CasellaM,etal.Towardsageneralizednon-linearacousticssolver[C]//Proceedingsof10thAIAA/CEASAeroacousticsConference,AIAA2004-3001, 2004.
[8]BattenP,GoldbergU,ChakravarthyS.Reconstructedsub-gridmethodsforacousticspredictionsatallReynoldsnumbers[C]//Proceedingsof8thAIAA/CEASAeroacousticsConference&Exhibit,AIAA2002-2511, 2002.
[9]DaSilvaCRI,DeAlmeidaO,BattenP.Investigationofanaxi-symmetricsubsonicturbulentjetusingcomputationalaeroacousticstools[C]//Proceedingsof13thAIAA/CEASAeroacousticsConference,AIAA2007-3656, 2007.
[10]HenshawMJ.M219cavitycase:verificationandvalidationdataforcomputationalunsteadyaerodynamics[R].ResearchandTechnologyOrganization,RTO-TR-26,AC/323(AVT)TP/19, 2002.
Nonlinear numerical simulation of cavity noise
WANG Yiding1,CHEN Binqi1, GUO Liang2, ZHONG Fanjun2,TONG Mingbo1
InordertoevaluatetheM219cavitynoiseat0.6, 0.85and1.35Machnumber,nonlinearacousticsolveriscombinedwithReynolds-averagedNavier-Stokesequations.TheflowfieldofacavityiscalculatedbymeansofReynolds-averagedNavier-Stokesequations,whichcontainsbasiccharacteristicsofaverageflowfieldandturbulencestatisticalaveragesolutionofstatisticsdescriptionofturbulencefluctuation.Noisesourceisrefactoredbythenonlinearacousticsolver.Spreadofpressurefluctuationissimulatedprecisely.Acomparisonshowsthatthesimulationresultsofnonlinearacousticsolveragreewellwiththeexperimentresults.Comparedwithdetachededdysimulation,nonlinearacousticsolvercangreatlyreducetheamountofmesh.Inaddition,themethodcanprovidesomereferenceforinternalweaponsbaydesign.
cavity;nonlinearity;source;turbulence;internalweaponsbay
2014-02-10
王一丁(1985—),男,四川樂山人,博士研究生,E-mail:wyding127@163.com;童明波(通信作者),男,教授,博士,博士生導師,E-mail: tongw@nuaa.edu.cn
10.11887/j.cn.201504025
http://journal.nudt.edu.cn
V
A

