基于變形能的粘彈性薄阻尼層結構阻尼特性分析

孫寶， 孫大剛， 宋勇， 李占龍， 王軍

(1.太原科技大學 機械工程學院， 山西 太原 030024；2.西安理工大學 機械與精密儀器工程學院， 陜西 西安 710048)

?

基于變形能的粘彈性薄阻尼層結構阻尼特性分析

孫寶1， 孫大剛1， 宋勇1， 李占龍2， 王軍1

(1.太原科技大學 機械工程學院， 山西 太原 030024；2.西安理工大學 機械與精密儀器工程學院， 陜西 西安 710048)

為了研究多彈性層約束阻尼結構的阻尼性能，將變形能原理應用于粘彈性薄阻尼層約束阻尼結構阻尼特性分析中，在一種薄阻尼層結構基礎上，給出了一種求解結構損耗因子的理論方法，獲得了結構損耗因子與材料損耗因子、阻尼結構剪切參數、剛度參數的耦聯關系。引入該理論，對層間厚度、相關阻尼參數進行了優化分析。針對兩個應用實例，通過有限元模態應變能法對比表明，變形能理論法計算結果與有限元法實驗結果比較一致，驗證了該理論方法的合理性。為研究多彈性層約束阻尼結構損耗因子的計算、機械產品的設計及結構改進等問題提供了一定的理論參考。

機械學； 薄阻尼層； 損耗因子； 變形能原理； 參數分析

0　引言

隨著兵器工業的日益發展，以及環境保護、節能降噪等領域要求標準的提高，兵工產品中許多振動、沖擊與噪聲的控制越來越成為一個復雜而迫切的問題。阻尼減振降噪技術是目前使用比較廣泛的一種對振動加以控制的方法。該技術充分利用阻尼耗能的原理，在測量、工藝、設計等各種技術問題上發揮阻尼在減振、降噪中的作用，以提高機械結構的抗振性，降低機械產品的噪聲，增強機械與機械系統的動態穩定性[1]。粘彈性材料約束阻尼結構增大了結構的損耗因子，避免了強度、剛度的損失，可以起到高效振動響應控制與結構承載功能一體化的作用。研究它對能量的耗散性能自然成為目前兵工領域中一類比較重要的問題[2]。

目前國內外針對阻尼結構損耗因子的研究主要分為解析法與數值法。解析法包括：復剛度法、模態分析法等。數值法主要包括有限元方法，具體有：復特征值法、模態應變能法、有限單元法等。工程應用中對約束阻尼結構的研究較多采用了有限元法[3-11]。文獻[3]采用復特征值法在阻尼狀態下求解運動方程，得到的特征值與特征向量均為復數，計算復雜性極高，同時對于一個具體的粘彈性材料，不具備推導其經典方程所需要的動態應力與應變特性。相比復特征值法，文獻[4]通過有限元模態分析找出阻尼結構的模態參數，在有限元模型中給出了每個單元的應變能，避免了大量的多特征值的計算。雖然該方法具有較高的精確性，能滿足一些工程的需要。但該方法屬于強制解耦的過程，將運動方程中的非對角元素加以忽略，往往使得計算結果比精確解偏小。在工程問題中，多數采用了復合單元法，文獻[5]利用該方法研究了粘彈性阻尼減振技術在導彈隔沖擊結構中的應用。文獻[6]利用有限元軟件，應用該方法研究了復合材料約束阻尼結構的參數優化設計問題。這種方法隨著結構層數的增多，有限元模型規模驟增，計算耗費多，而且阻尼膠膜厚度較小，體單元模擬時單元形狀誤差偏大，并不利于阻尼結構參數的優化設計。文獻[7]提出了一種基于分層離散理論的有限單元法并且用于復雜多層阻尼結構的動態特性和損耗因子的預測，與傳統的復合單元法相比，該方法計算耗費明顯降低，但實驗測定受到摩擦阻尼、邊界條件理想化、數據處理等因素的影響，而且隨著模態的增加，實驗誤差也比較明顯。

綜上所述，有限元法雖然快速、簡單，但需要編程、建模等工作，由于受到結構總剛度矩陣規模的影響，在利用有限元軟件進行分析時，計算耗費龐大，例如文獻[7]中對固支梁損耗因子的計算問題，利用復合單元法建模，若采用75個板元，50個體單元和104個多點的約束單元，結構整體的剛度矩陣的維數將達到720，且隨著層數的增加，計算復雜性、耗費將更為龐大。對于多層約束阻尼結構，材料具有沿厚度方向的不連續性，多層間剛度的不均勻性以及粘彈性阻尼機理的復雜性等特點。目前對該類結構的理論分析方法仍不成熟，在很大程度上限制了其在兵工、機械工程等領域中的有效應用。

本文基于變形能原理，針對一種薄阻尼層約束阻尼結構，分析計算了兩彈性層約束阻尼結構的結構損耗因子。變形能法能直觀、明確地反映結構損耗因子對消振能力的影響作用。經過分析，得到了損耗因子與各阻尼參數間的耦聯關系，為約束阻尼結構的正確設計、阻尼參數的優化分析提供一種思路。

1　結構損耗因子的分析計算

1.1變形能原理

損耗因子η表示結構耗散能和總的彈性變形能的比值。

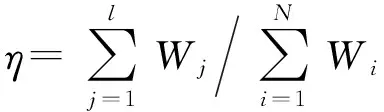
(1)

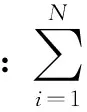
η最直接最明確地表現了阻尼和消振作用的密切聯系，概念清楚，數學表達式簡潔，尤其對于幾種阻尼耗能方式滲合在一起的復雜結構，只要做能量分析，就可以得到確切的計算結果。

對于一個約束阻尼結構，變形能包括拉伸變形能We、彎曲變形能Wf、阻尼層彈性剪切變形能Ws三部分。考慮阻尼層拉伸變形的影響和基層、約束層的材料阻尼，結構總的耗散能量Wd為

Wd=α(We+Wf)+βWs，

(2)

式中：α為耗能結構的拉伸損耗因子；β為耗能結構的剪切損耗因子。

對于基層和約束層，當發生彎曲時，其界面上既有彎矩，又有剪力，所以在截面上既存在正應力，又存在剪應力。當彈性層為金屬結構時，忽略剪切應變，此時，約束阻尼結構總的變形能W為

W=We+Wf+Ws.

(3)

若僅考慮阻尼附加結構的橫向彎曲振動，那么，對任何附加阻尼結構的結構損耗因子η均可表示為

(4)

從(4)式可以看出，結構耗散能量Wd的提高，將有利于提高約束阻尼結構的損耗因子η. 本文的目的正是針對粘彈性相關材料的阻尼參數，對于一種薄阻尼層約束阻尼結構，合理優化層間厚度，提高結構耗散能量Wd，以使結構損耗因子η可以達到最大。

1.2結構損耗因子的分析計算

分析中采用文獻[1]中Kerwin的理論假設：

1)以彈性組合夾層板為計算對象，板的邊界條件為兩端簡支；

2)阻尼層和彈性層作相同曲率的彎曲振動，并忽略相對伸長；

3)結構耗能利用彎曲波全波長上的平均耗能來衡量；

4)對于厚度不同的彈性層，所有組合層也具備完全相同的振動模態；

5)在彈性梁的全部面積上均有附加的阻尼層，且僅計入阻尼層的剪切耗能。

6)阻尼層較軟，忽略阻尼層中平行于Oxy平面的應力，即假定σx=σy=τxy=0；

7)僅考慮對稱變形，所以在阻尼層中z方向應變和應力分量很小，可以忽略；

8)各層之間理想結合，無相對滑動。

采取如圖1所示的一般約束阻尼結構形式。外層1是需要消振的任意結構，內層3是收到外層1包容的約束結構，阻尼層2處于內、外層之間。

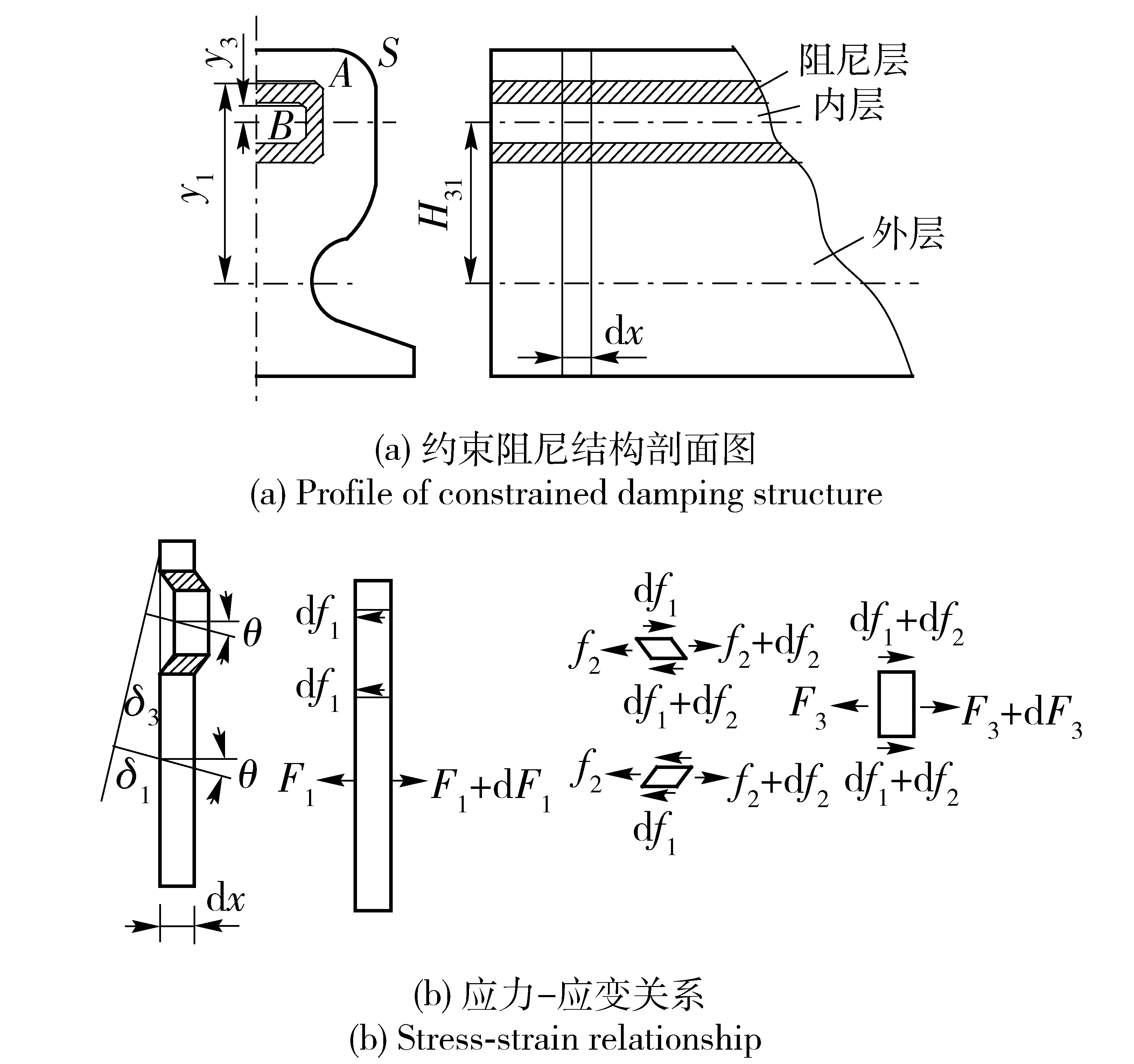
圖1　約束阻尼結構應力- 應變關系Fig.1　Stress-strain relationship of constrained damping structure

假設3個結構件不發生扭曲的動態變形，也不產生交界面的滑動。當結構發生彎曲振動時，忽略外層1和約束層3的剪切變形能，對于這種3層結構，可按(5)式計算結構損耗因子η.

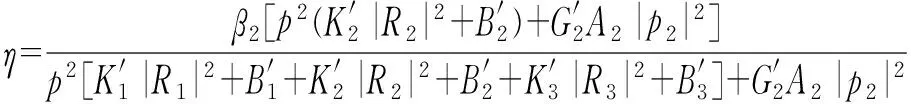
(5)

式中：p為波數；K′為單位長度復拉伸剛度的實部；A2為第2個子結構的橫截面積；B′為復彎曲剛度的實部；G′2為復剪切模量的實部；R為諧和變化系數。

利用軸向拉力的平衡方程以及剪切應變的關系式，可求得R1、R2、R3的關系式：

K′1R1+K′2R2+K′3R3=0.

(6)

為了得到位移平衡方程式，在阻尼層的任意特定位置(圖1(a)中的截面AB)上求平均位移，從圖2(a)的幾何關系可知：

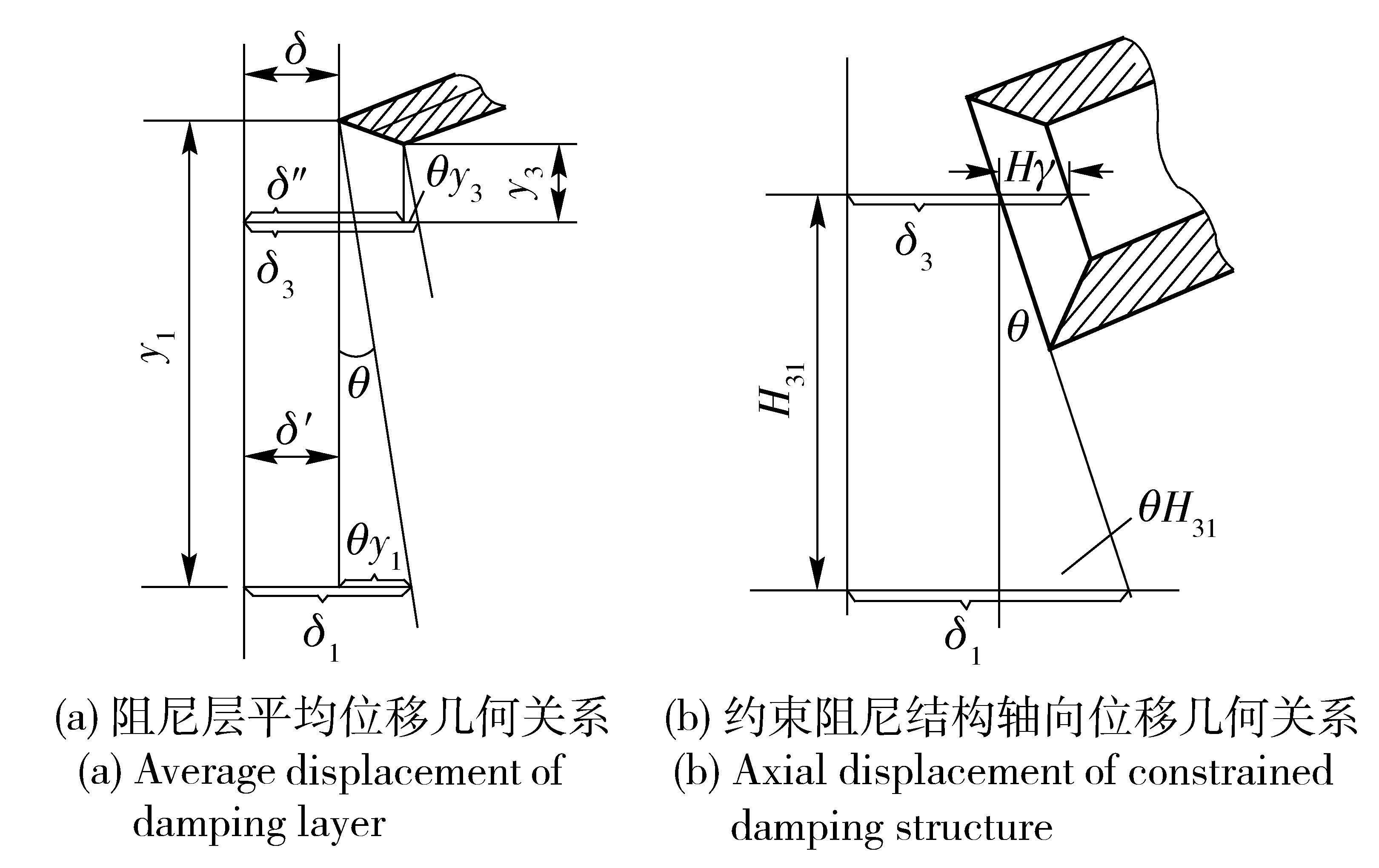
圖2　位移之間的幾何關系Fig.2　Displacement geometric relationship

(7)

式中：θ為彎曲變形的角位移；δ1、δ3為構件內層、外層重心的中心軸向位移。

將阻尼層環線S(圖1(a)所示)上的各點位移δ在全長b上取平均值，則

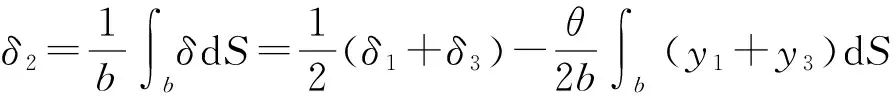
(8)

式中：y1、y3分別為A、B點到構件內層、外層重心的距離。

又由于δn=θRn，n=1,2,3，代入(8)式，可得

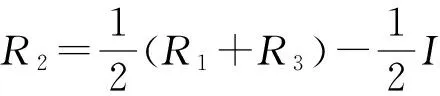
(9)

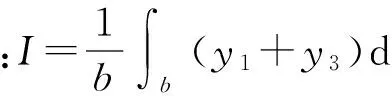
下面通過剪力平衡來得到第3個方程式。按照圖1作用于阻尼層的平均剪應力τ為

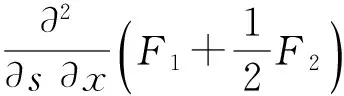
(10)

式中：Fn為作用于第n個結構件上的軸向力；fn為單位長度的力，fn=Fn/b.

由圖2(b)所示，剪切應變和結構件內層、外層的軸向位移δ1、δ3之間的幾何關系為

δ1-θH31=δ3-Hγ2.

(11)

由于τ=G2γ2,將(11)式代入，得

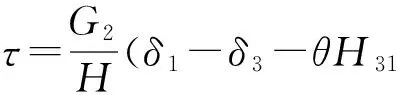
(12)

進一步計算，并加以改寫得

(13)

聯立(6)式、(9)式及(13)式，便可求得3個未知數Rn(n=1,2,3).

經過合理的假設，(5)式可改寫為

(14)

在實際結構中，由于阻尼層剛度相比內層、外層很低，即

K′1?|K′2|，K′3?|K′2|.

經過合理的簡化、整理，(14)式可變為

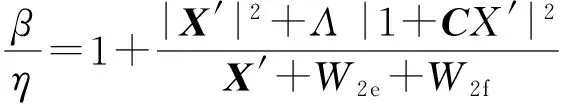
(15)

對于阻尼層結構，X′、W2e、W2f分別代表剪切變形能、拉伸變形能及彎曲變形能，進一步簡化整理，W2e、W2f可忽略不計，將Λ=1/Y代入(15)式，最后可求得結構損耗因子η：

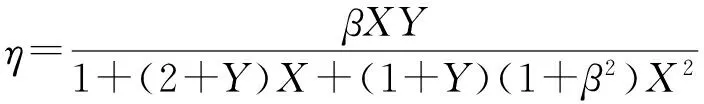
(16)

式中：

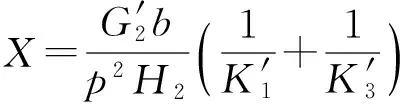
(17)

(18)

可見，對于一個約束阻尼結構，利用變形能法求得的結構損耗因子η取決于材料損耗因子β、剪切參數X及剛度參數Y三方面因素。下面就相關阻尼參數的合理選擇對阻尼性能的影響作出分析。

2　阻尼性能分析

層間厚度的控制是阻尼減振優化設計中的主要方面，也是影響阻尼減振耗散性能的主要約束條件之一。下面就一種典型的兩彈性層薄阻尼層結構，如圖3所示，在相關結構、材料參數下研究層間厚度對粘彈性約束阻尼結構動態力學性能的影響。

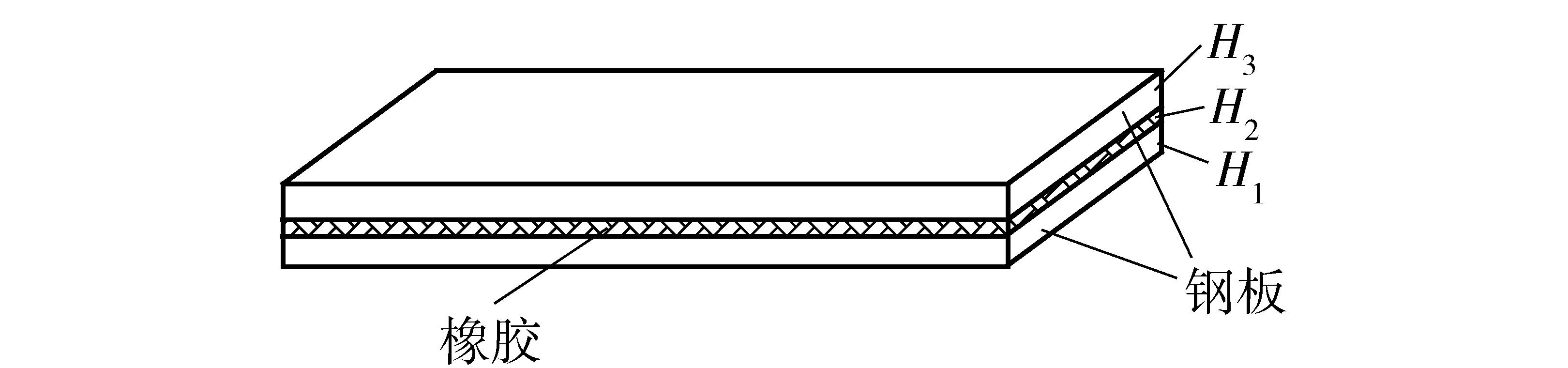
圖3　薄阻尼層約束阻尼結構Fig.3　Constrained damping structure of thin damping layer

首先給出上述結構損耗因子的計算框圖(見圖4)，從中可以分析得到當結構損耗因子η=ηmax時，所對應的剪切參數X=Xopt，剛度參數Y=Ymax以及相關阻尼參數、層間厚度的最優值。

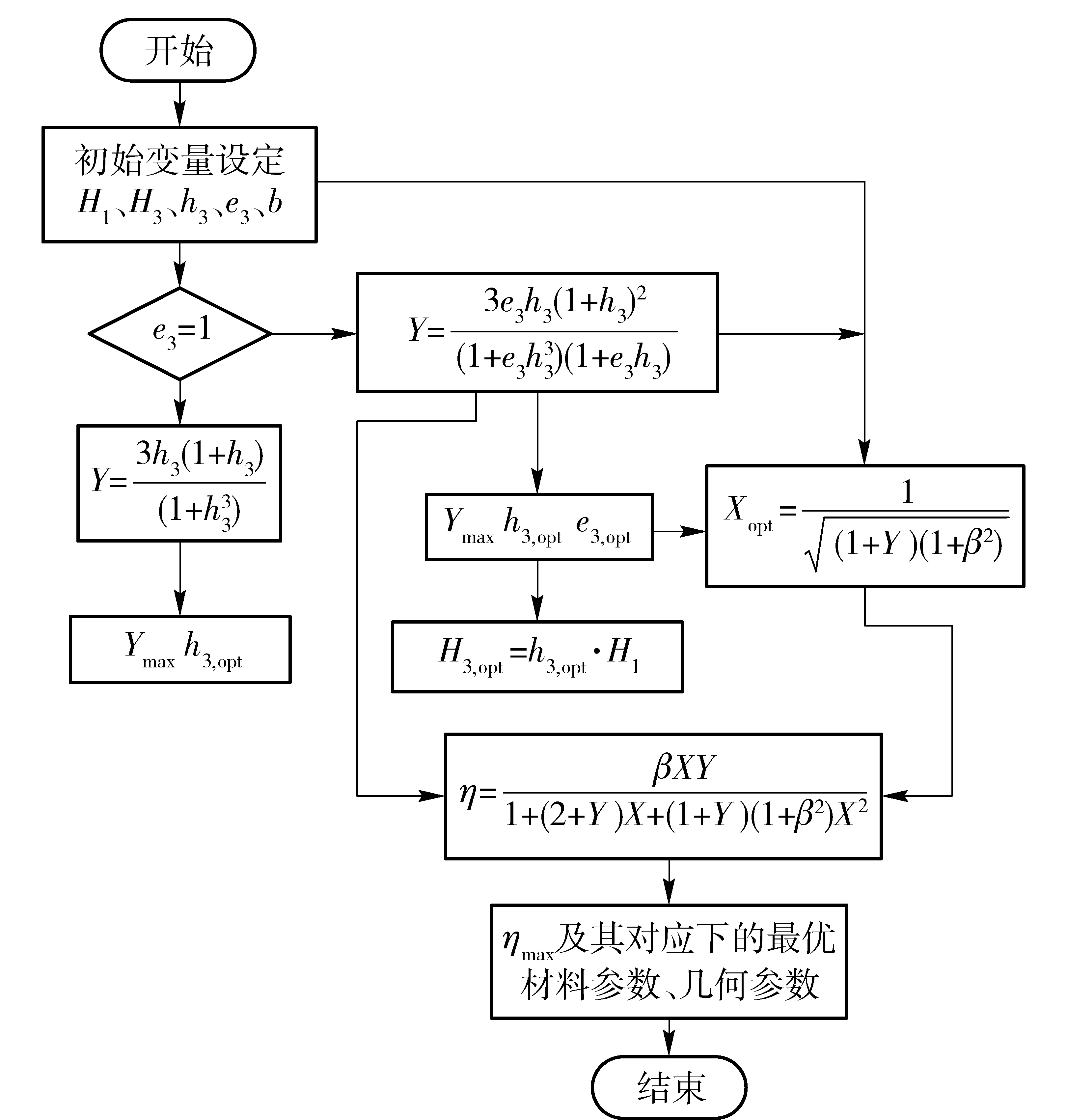
圖4　薄阻尼層結構損耗因子的計算框圖Fig.4　The calculation block diagram of thin layer damping structure loss factor

2.1剛度參數Y分析

由(18)式已知

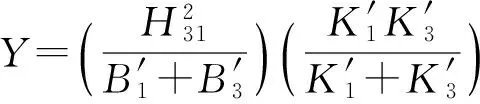
(19)

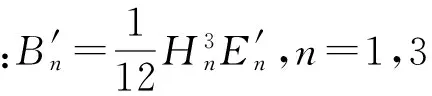
對于薄阻尼層結構，h2?1，令h2=0，此時得到剛度參數Y為

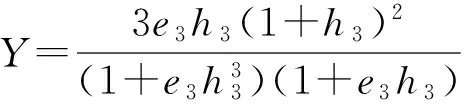
(20)

特殊地若約束層結構外層、內層取相同的材料，即E′3=E′1或e3=1，則

(21)

將(21)式對h3求導，并求極值，很容易可得當h3=1時Y有極大值Ymax，將h3=1代入(21)式，Ymax=3. 對于(20)式，采取同樣求極值的辦法可得到相應Y=Ymax時對應h3=h3，opt. 圖5給出了當e3分別等于0.01、0.125、1、10、100時，Y與h3的函數曲線，從圖中可以看出剛度參數Y與約束層厚度比h3的變化規律，進而體現了約束層厚度對剛度參數Y的影響。

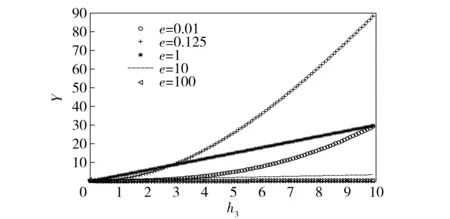
圖5　Y與h3的函數關系曲線Fig.5　Function relation between Y and h3

2.2剪切參數X分析

對于(16)式，當給定一組不同的β及Y，此時結構損耗因子η與剪切參數X的關系為

(22)

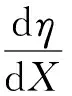
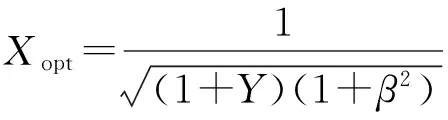
(23)

所以，由(23)式與(17)式聯系起來可以看出，當給定阻尼材料的G′2值，結構外層、內層的幾何尺寸與材料，在一定的激勵頻率f下，為了得到最大的結構損耗因子ηmax，要按(23)式優化X，使得剪切參數最優值X=Xopt. 下面給出X關于約束層厚度比h3的優化曲線，如圖6所示。

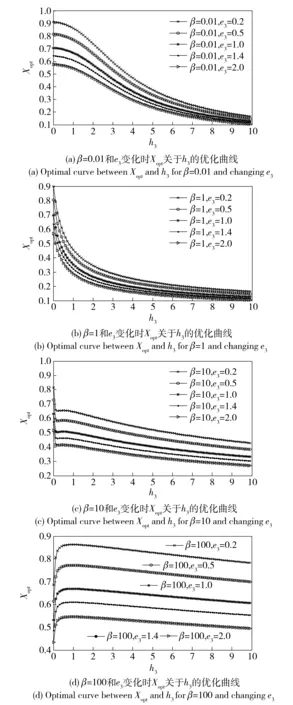
圖6　Xopt與h3的函數曲線Fig.6　Function relation between Xopt and h3

將(23)式代入(16)式，得到ηmax:

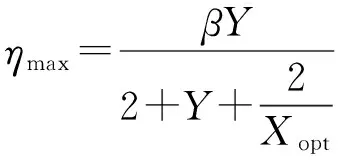
(24)

由(24)式，當X=Xopt時，在β一定時，ηmax是Y的函數，且ηmax隨Y的增加而增加。但隨著幾何尺寸的變化，例如無限制增加約束層的厚度，并不能使Y值持續增加。所以，很有必要對約束層厚度加以優化。

2.3約束層厚度的優化

由以上分析，若與剛度參數Ymax相對應的h3，opt求得，此時兩個約束層的最優厚度關系為

H3，opt=h3，optH1.

(25)

下面給出剛度參數η關于約束層厚度比h3的優化曲線，可以直觀地看出約束層厚度對損耗因子的影響作用，如圖7所示。

圖7　η與h3的函數曲線Fig.7　Function relation between η and h3

由以上分析，特殊地，若約束層結構外層、內層材料相同，則H3，opt=H1. 當厚度相等時，此時的約束阻尼結構將有最好的耗散性能，所以在工程實際設計中，往往可以設計為一種對稱的約束阻尼結構，以獲得較大的結構損耗因子η.

2.4損耗因子關于β、X、Y的三維效果圖

由(22)式作出了當β分別為0.2、1、1.4、2時，η關于X與Y的優化圖(見圖8)。可直觀看出η與X、Y的變化規律。

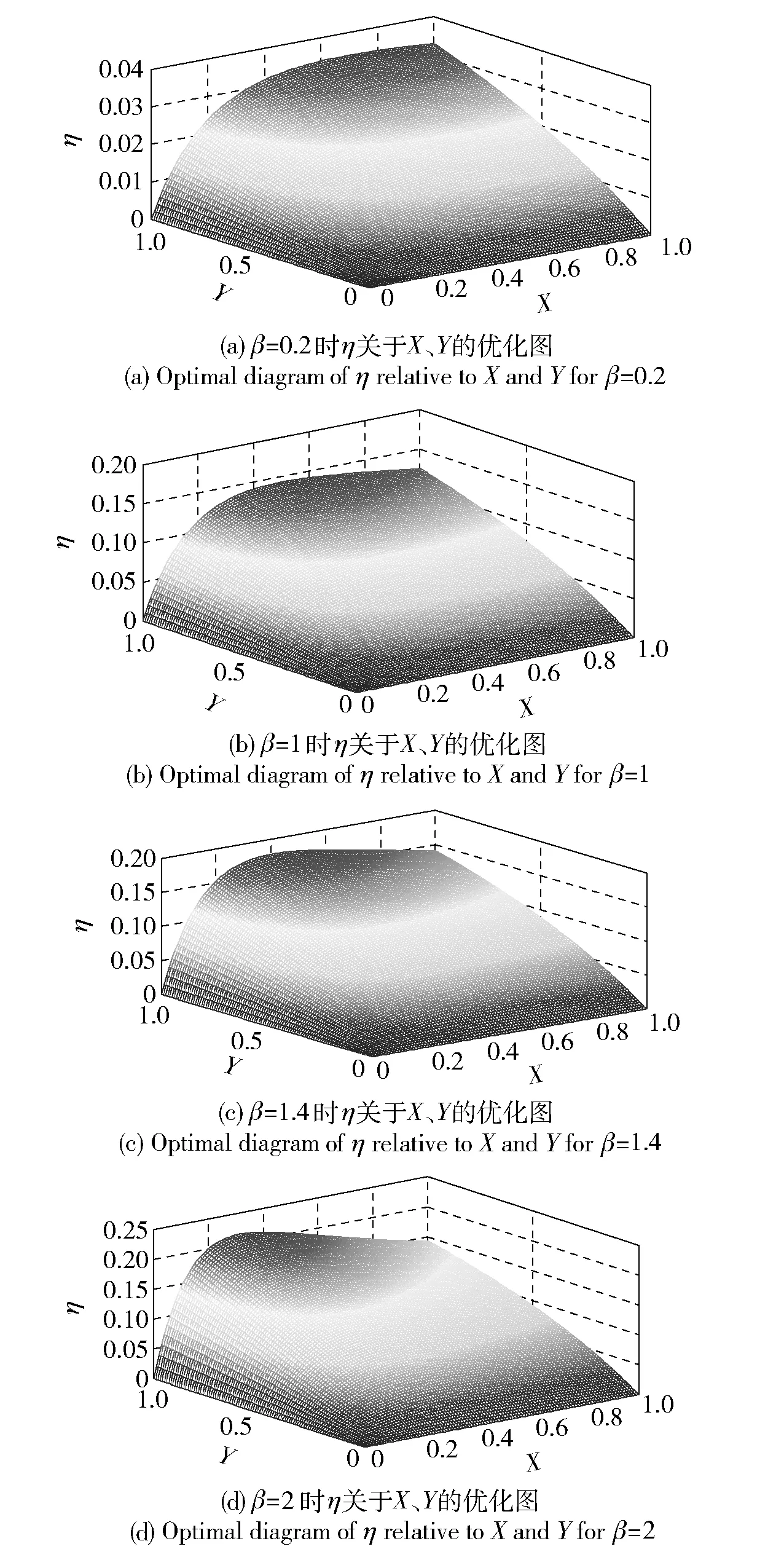
圖8　η關于X、Y的優化圖Fig.8　Optimal diagram of η relative to X,Y

3　有限元驗證

3.1算例

板的幾何尺寸：長為213 mm，寬為127 mm，基層和基層厚度均為2.0 mm，阻尼層厚度為0.5 mm. 約束層和基層均采用鋁，材料性能參數：彈性模量為72 GPa，密度為2.7 g/cm3，泊松比為0.33. 阻尼層材料為ZN-1，密度為0.98 g/cm3，剪切模量為1.4 MPa，材料損耗因子η=1.20.

算例1采用兩端部固支矩形截面阻尼夾層結構，總層數為3層。應用有限元進行建模時，阻尼層采用Hex 8六面體單元，彈性層采用CQuad 4板單元。為了確保層間位移的協調，本文定義了板單元節點與對應實體單元節點間的多點約束單元(Rbe 2)，有限元模型示意圖如圖9所示。

圖9　阻尼夾層結構有限元模型Fig.9　Damped sandwich structural finite element model

表1給出了當約束層厚度H3變化時，采用本文的變形能法與有限元方法對結構損耗因子的計算結果。

對比結果表明，約束層厚度為2.0 mm時，結構為一種對稱的約束阻尼結構，此時的損耗因子最大，理論計算與有限元法計算結果比較接近。驗證了本文理論方法的合理性。誤差產生的原因及實驗結果普遍比理論計算結果大的原因可能是在理論分析計算時并沒有充分考慮到結構約束處的摩擦阻尼；當約束層厚度發生變化時，也會影響阻尼材料的相關物理性質。

3.2算例2

本文引述文獻[7]關于邊界條件影響的結論：邊界條件的變化并不影響結構的最大模態損耗因子ηmax，但會導致當結構出現最大模態損耗因子ηmax的頻率fmax移動。根據此觀點，在上述介紹的理論假設前提下，利用本文提出的變形能理論方法進行計算。算例如下：

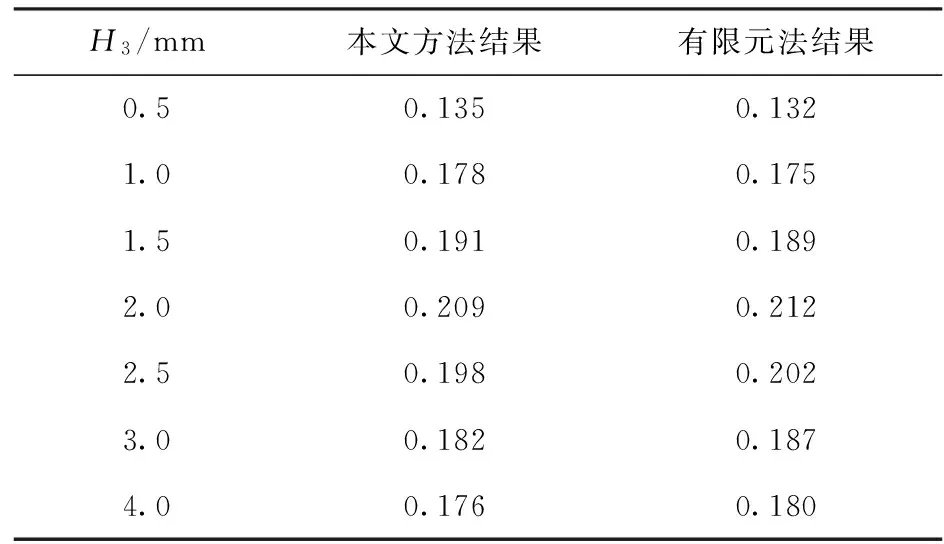
表1　不同約束層厚度下的結構損耗因子η

選用Johnson給出的一個算例 ，0.304 8 m×0.348 0 m的各向同性的四邊簡支夾層板結構，基層與約束層厚度均為0.762 mm，彈性模量均為E=68.9 GPa，泊松比均為μ=0.30，密度均為ρf=2 740 g/cm3. 阻尼層厚度為0.254 mm，剪切模量為0.896 MPa、泊松比均為μ=0.49，密度為ρc=999 g/cm3. 損耗因子η=0.50.

表2給出了利用本文理論方法與有限元模態應變能法對該結構損耗因子和固有頻率的計算結果。利用Ansys軟件進行模態分析，計算得到模態損耗因子。分析模型為三維實體，單元為SOLID45. 實體單元具有8個節點，每個節點具有3個自由度，分別是x,y,z的平動自由度，輸入的材料特性為各向同性。在實際中，經常從質量角度或者實際應用的層面出發，以阻尼帶的形式進行局部阻尼的處理，采用變形能理論加以分析。

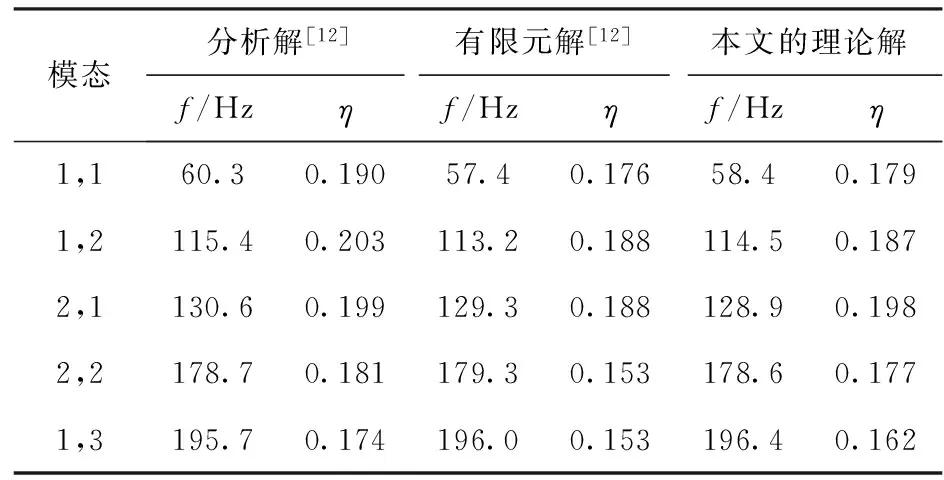
表2　本文結果與Ansys計算結果的比較

對比表明，理論計算結果與Ansys分析結果還是比較接近的，誤差均小于5%. 說明本文方法能滿足工程設計的要求，也驗證了本文方法的正確性。分析兩種方法存在誤差的主要原因可能是由于在有限元計算時對阻尼層既考慮了剪切效應，又考慮了擠壓效應，而本文變形能法采用Kerwin的復剛度法假設理論卻只考慮了阻尼層的剪切效應。

4　結論

1)基于變形能原理，針對粘彈性薄阻尼層結構給出一種結構損耗因子的理論計算方法，并分析了約束層厚度的變化對阻尼性能的影響。

2)將本文建立的變形能法與有限元法應用于兩個具體的薄阻尼層約束阻尼結構損耗因子的計算中，對比結果表明變形能法具有較高的計算精度。

3)本文所采用的變形能法，概念清晰，不僅可應用于具有兩彈性層的粘彈性薄阻尼層結構中，也可推廣至更為復雜的薄阻尼多層約束阻尼結構中，具有一定的理論參考價值。

References)

[1]戴德沛. 阻尼減振降噪技術[M].西安:西安交通大學，1986.

DAI De-pei. Damping technology in reduction for vibration and noise[M]. Xi’an: Xi’an Jiaotong University Press,1986. (in Chinese)

[2]桂洪斌,趙德有,鄭云龍.粘彈性阻尼層結構動力學問題有限元綜述[J]. 振動與沖擊, 2001, 20(1):44-47.

GUI Hong-bin, ZHAO De-you, ZHENG Yun-long. A review finite element method analyzing dynamic problem of structure with viscoelastic damped layer[J]. Jounal of Vibration and Shock, 2001,20(1):44-47. (in Chinese)

[3]王正興,代會軍. 粘彈性阻尼材料在板結構中的優化計算[J].噪聲與振動控制, 2000, 18(6):21-30.

WANG Zheng-xing, DAI Hui-jun. An optimized computation for damping elastic plank structure[J]. Noise and Vibration Control,2000,18(6):21-30. (in Chinese)

[4]申顏利,楊慶山,田玉基.模態應變能方法精確性和適用性研究[J].工程力學,2008,25(6):18-21.

SHEN Yan-li,YANG Qing-shan, TIAN Yu-ji.Study of accuracy and applicability of modal strain enegy method[J]. Engineering Mechanics, 2008,25(6):18-21. (in Chinese)

[5]任懷宇. 粘彈性阻尼減振在導彈隔沖擊結構中的應用 [J]. 宇航學報, 2007,28(6):1494-1499.

REN Huai-yu. The application of viscoelastic damping vibration suppression for shock isolation structure of multistage missile[J]. Journal of Astronautics,2007,28(6):1494-1499. (in Chinese)

[6]Yamaguchi T, Kurosawa Y, Enomoto H. Damping vibration analysis using finite element method with approximated with approximated model damping for automotive double walls with a porous marerial[J]. Journal of Sound and Vibration,2009,325(1/2):436-450.

[7]徐超, 張醒.多粘彈性膠膜夾層約束阻尼梁損耗因子分析[J].宇航學報,2009,30(2):458-462.XU Chao,ZHANG Xing. Modal loss factor analysis for sandwich beams embedded with multiple viscoelastic damping thin layers[J].Journal of Astronautics,2009,30(2):458-462. (in Chinese)

[8]Mehata C R,Tewari V K. Damping characteristics of seat cushion materials for tractor ride comfort[J].Journal of Terramchanics,2010,47(6):401-406.

[9]Zhang S H, Ceng H L. A study on the damping characteristics of laminated composites with integral viscoelastic layers[J].Composite Structures, 2006,74:63-69.

[10]Jean-marie B, Youssef S. Damping analysis of unidirectional glass fiber compersite with interleaved viscoelastic layers experimental investigation and discussion[J].Journal of Composite Material, 2006,21:1911-1932.

[11]郭中澤，羅景潤，陳裕澤.約束阻尼結構的模態損耗因子計算的一種修正方法[J].兵工學報,2006,27(6):1064-1067.

GUO Zhong-ze,LUO Jing-run,CHEN Yu-ze.An improved method of predicting the modal loss factors of constrained damping structure[J].Acta Armamentarii, 2006,27(6):1064-1067. (in Chinese)

[12]Johnson C D, Kienholz D A. Finite element prediction of damping in structures with constrained vicoelastic layers[J]. AIAA Journal, 1982, 20(9):1284-1290.

Damping Characteristics Analysis of Viscoelatic Thin Damping Layer Structure Based on Deformation Energy Method

SUN Bao1, SUN Da-gang1, SONG Yong1, LI Zhan-long2, WANG Jun1

(1.School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, Shanxi, China; 2.Mechanical Instrumental Engineering College, Xi’an University of Technology, Xi’an 710048, Shaanxi, China)

In order to study the damping characteristics of constrained damping structure with multiple elastic layers, a calculation method of a constrained damping structure loss factor is set up based on the principle of deformation energy. And the coupling relation among structure loss factor, material loss factor, shear parameter of damping structure and stiffness parameter is got. The proposed method is introduced into the optimization analysis of the interlayer thickness, structure and related material damping parameter. The finite element modal strain energy method is used to compare two practical examples. The comparative result shows that the calculated results of the theoretical method is in agreement with the experimental results obtained by finite element method.

mechanics; thin damping layer; loss factor; deformation energy; parameter analysis

2014-06-27

國家青年科學基金項目(51305288、51405323)；山西省回國留學人員科研資助項目(2012-073)；山西省青年科學基金項目(2013021020-1)

孫寶(1981—)，男，講師， 博士研究生。E-mail：bao810321@163.com；

孫大剛(1955—)， 男， 教授， 博士生導師。 E-mail: 793456439@qq.com

TB153

A

1000-1093(2015)04-0744-08

10.3969/j.issn.1000-1093.2015.04.024