基于小波去噪與DRNN的光纖陀螺隨機誤差建模研究

王慶賀

(中國空空導彈研究院，河南 洛陽 471009)

0 引 言

陀螺儀的測量精度直接影響導航系統(tǒng)的性能，對其誤差的研究至關(guān)重要。陀螺的誤差可分為系統(tǒng)性誤差與隨機性誤差，其中又以具有復雜特性的隨機誤差作為研究的重點。隨機誤差為有害噪聲，為減小或者消除隨機誤差對慣導系統(tǒng)的影響，必須研究隨機誤差的特性并建模。隨著隨機誤差理論研究的不斷發(fā)展，Allan 方差、ARMA、小波理論、神經(jīng)網(wǎng)絡(luò)等方法已經(jīng)被應用到陀螺的隨機誤差分析和建模中［1－4］。目前常用的陀螺隨機誤差模型有白噪聲與有色噪聲的組合模型、ARMA 模型、神經(jīng)網(wǎng)絡(luò)模型等。然而陀螺的隨機誤差是復雜的噪聲復合，既有白噪聲又有不同特點的有色噪聲，低頻噪聲與高頻噪聲并存，且其時序數(shù)據(jù)通常為非平穩(wěn)數(shù)據(jù)。這種復雜的特性使隨機誤差的建模存在建模難度大和建模精度不高等問題。針對這些問題，建模時選取不同的理論方法來組合應用，取得了良好的效果。例如在時間序列研究中，小波理論和ARMA 方法是最常用的組合［5－7］，這對陀螺隨機誤差的建模具有借鑒意義［8－10］。但ARMA 模型為線性模型且建模操作復雜，相對于ARMA 建模，神經(jīng)網(wǎng)絡(luò)具有任意非線性映射的能力。對角神經(jīng)網(wǎng)絡(luò)(DRNN)是一種局部內(nèi)遞歸神經(jīng)網(wǎng)絡(luò)，結(jié)構(gòu)簡單且具有良好的動態(tài)特性，利用其建模時，不必如ARMA 一樣進行模型假設(shè)，簡化了建模過程。

因此，本文采用這種理論組合的思路，選擇小波閾值去噪和DRNN 對陀螺隨機誤差進行建模。首先，根據(jù)陀螺隨機誤差的特點，將其分為高頻部分和低頻部分;然后，采用小波去噪方法去除高頻噪聲，減小誤差的復雜程度，再用DRNN 對去噪后的低頻部分進行建模;最后，對陀螺的實測數(shù)據(jù)進行仿真分析，結(jié)果表明本文所提出的建模方法是行之有效的。

1 基于小波分析的閥值降噪

1.1 小波變換

小波變換是一個在時頻域上都具有良好的局部特性的小波函數(shù)和一個平方可積函數(shù)的內(nèi)積［12］，如式(1)所示:

其中:f(t)為原始信號;φa，b為小波序列，稱為小波;a(＞0)為尺度因子;b 為位移因子;表示復數(shù)共軛。φ(t)通過a，b 進行伸縮和平移。位移因子b 起著平移作用。尺度因子a 不僅會改變φa，b的頻譜結(jié)構(gòu)，還會改變窗口的大小和形狀。a 大時，對應低頻部分，頻率分辨率高，時間分辨率低;反之，對應高頻部分，頻率分辨率低，時間分辨率高。

在實際應用小波變換時是必須離散化的。可取整數(shù)m，n，取常數(shù)a0＞1，b0＞0，對a，b 進行離散化處理，如式(2)所示:

通常取a0= 2，b0= 1，稱為二進小波變換，此時離散小波函數(shù)如下:

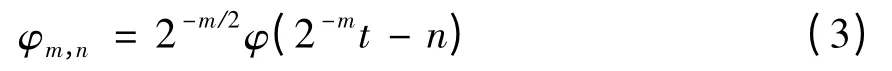
相應的離散小波變換為

天津市高等學校師資培訓中心（以下簡稱天津市中心）成立于1990年，受天津市教委和天津師范大學雙重領(lǐng)導。中心下設(shè)行政辦公室、崗前培訓辦公室、信息技術(shù)部、教師資格認定辦公室，當前業(yè)務(wù)以崗前培訓、教師資格認定、高校教師網(wǎng)絡(luò)培訓為主。

小波變換常采用Mallat 算法［11］。Mallat 算法為一種塔式分解算法，分解算法如下:

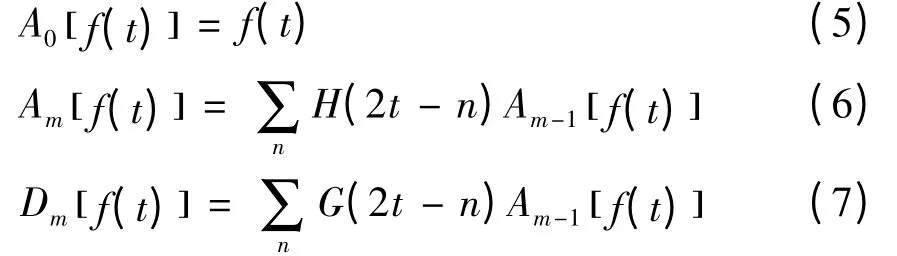
其中:f(t)為原始信號，t = 1，2，3，…，Τ;m 為小波變換分解層數(shù)，m = 1，2，3，…，M，其中M =log2Τ;H，G 分別為低頻分解濾波器系數(shù)和高頻分解濾波器系數(shù);Am，Dm分別為分解得到的低頻小波系數(shù)和高頻小波系數(shù)。Mallat 算法的重構(gòu)如下:

1.2 小波閥值去噪

小波去噪方法可分為三大類［11］。第一類為小波變換模極大值去噪;第二類為基于小波變換的相關(guān)去噪;第三類為閥值去噪，為最常用方法。小波閥值去噪基于多分小波變換:不同尺度的小波變換會表現(xiàn)出不同的形態(tài)，構(gòu)造出相適應的規(guī)則，以減小甚至完全置零噪聲產(chǎn)生的系數(shù)，同時最大限度保留有用信號的系數(shù)。小波閥值去噪的步驟歸納如下:

(1)選取合適的小波基函數(shù)和分解層數(shù)，對信號進行小波分解;

(2)根據(jù)信號和噪聲的不同頻率特點，對分解得到的系數(shù)進行閥值量化。小波變換較為細致地劃分了信號不同頻率成分，在不干擾有用信號的基礎(chǔ)下，對噪聲系數(shù)進行閥值量化完全可行;

(3)重構(gòu)信號。

小波閥值去噪的關(guān)鍵是如何選取閥值，如何進行閥值的量化。對于閥值確定規(guī)則，閥值量化方法，文獻［11］有非常全面的介紹，在此不再贅述。

2 對角神經(jīng)網(wǎng)絡(luò)(DRNN)

對角遞歸神經(jīng)網(wǎng)絡(luò)(Diagonal Recurrent Neural Network，DRNN)為內(nèi)部遞歸神經(jīng)網(wǎng)絡(luò)，其隱層神經(jīng)元只接收自我延遲反饋且與其他同層神經(jīng)元無反饋連接。相比全局反饋遞歸網(wǎng)絡(luò)(如Elman 網(wǎng)絡(luò)等)，DRNN 的結(jié)構(gòu)更簡單，這使其在保留動態(tài)映射能力的同時有更快的學習速度。DRNN 的網(wǎng)絡(luò)結(jié)構(gòu)如圖1 所示。

圖1 DRNN 結(jié)構(gòu)圖

圖1 所示為三層DRNN 網(wǎng)絡(luò)，設(shè)輸入神經(jīng)元為n個，隱層神經(jīng)元為h個，一個輸出神經(jīng)元。DRNN的數(shù)學模型如下:

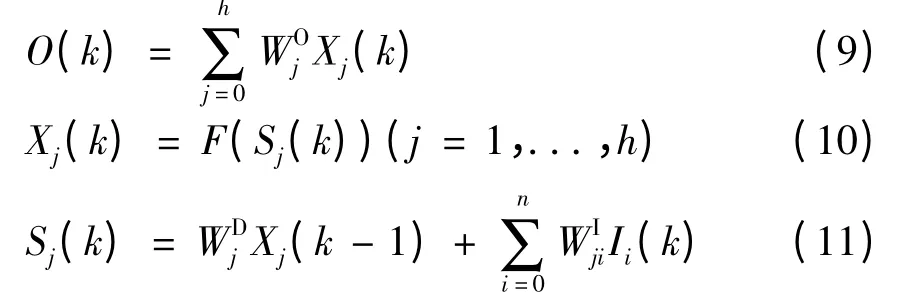
式中:O(k)為DRNN 輸出;Sj(k)，Xj(k)分別為隱層第j個神經(jīng)元的輸入與輸出;Ii(k)為第i個輸入神經(jīng)元的輸入;下標為零輸入的代表偏置輸入，賦值為1。WI為輸入層至隱層的權(quán)值矩陣與偏置值;WO為隱層至輸出層的權(quán)值矩陣與偏置值;為隱層神經(jīng)元自反饋的權(quán)值與偏置值。隱層神經(jīng)元F(x)取S 函數(shù)，輸出神經(jīng)元取purelin 函數(shù)為激活函數(shù)。

建模時，I(τ)為DRNN 網(wǎng)絡(luò)τ 時刻的輸入，為了進行預測，取其中)代表t 時刻輸出的估計值，且有n = 2。如此可使輸出為1)的函數(shù)，且不必如外遞歸網(wǎng)絡(luò)或ARMA 確定模型的階次［13］。此時網(wǎng)絡(luò)輸出為τ 時刻期望輸出的估計值，從而實現(xiàn)預測。

DRNN 的學習算法可使用通過時間的反向傳播(BPTT)算法(BP 算法擴展形成的)。此外，引入LM 算法優(yōu)化網(wǎng)絡(luò)的訓練會比單獨使用BP 算法有更快的收斂速度［14］。本文采用適用于DRNN 的LMBP 算法為訓練算法。

對于DRNN 網(wǎng)絡(luò)，數(shù)學描述如式(9)～(11)所示。取性能函數(shù)如下:

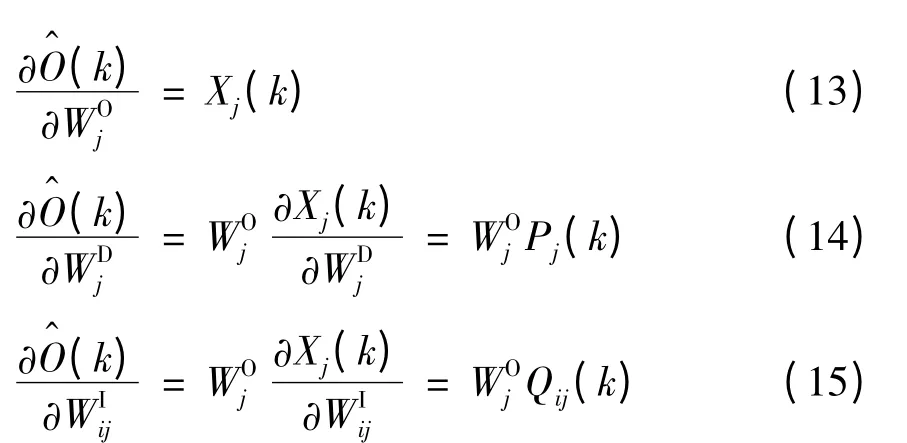
其中，

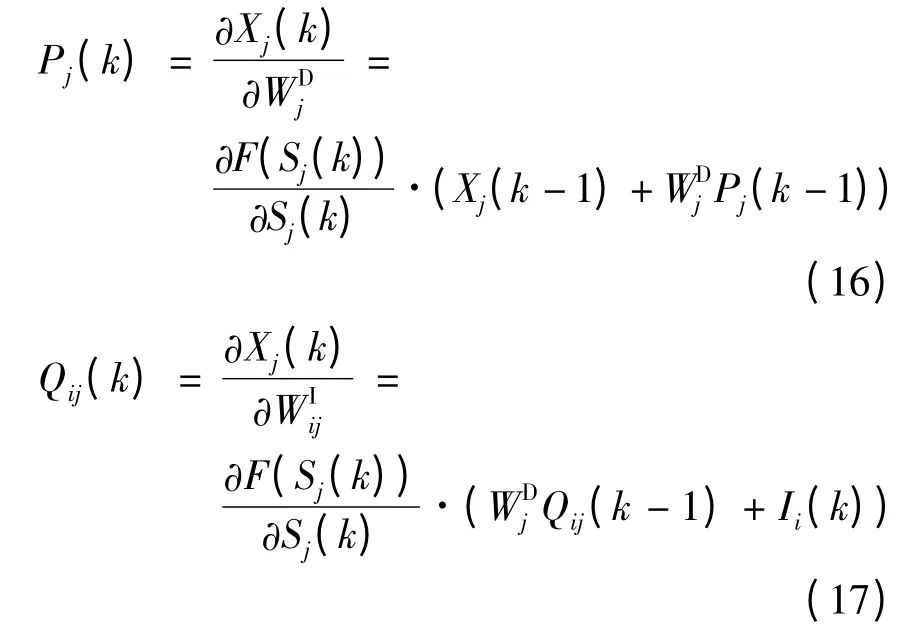
由式(12)～(17)可以求得雅可比矩陣，從而推導出DRNN 的LM 算法。

3 基于小波去噪與DRNN 的隨機誤差建模仿真

由于工作原理和環(huán)境干擾等原因，光纖陀螺存在多種確定性誤差和隨機性誤差，輸出信號是非平穩(wěn)且弱非線性的，傳統(tǒng)去噪方法效果并不理想。陀螺隨機誤差主要包括量化噪聲，角度隨機游走，零偏不穩(wěn)定性(1/f 噪聲)，角速率隨機游走，速率斜坡，正弦分量等［15］。本文以光纖陀螺實測數(shù)據(jù)為基礎(chǔ)，對隨機誤差進行分析。

圖2 為一組光纖陀螺在靜基座下X 軸的隨機誤差數(shù)據(jù)。陀螺采樣周期為1 Hz，采樣時間為7 h，現(xiàn)截取陀螺穩(wěn)定運行后14 000 s 的數(shù)據(jù)。

圖2 光纖陀螺隨機誤差

對于所采集的隨機誤差數(shù)據(jù)，其特性可從時域與頻域兩方面進行分析。時域上，可采用相關(guān)性分析法;頻域上，可進行功率譜密度(PSD)分析，能夠更好的辨識出周期性誤差。此外，Allan 方差方法是由David Allan 提出的，是一種時域分析方法，能夠細致地對噪聲統(tǒng)計特性的貢獻進行表征與辨識，而且具有便于計算、易于分離等優(yōu)點［16］。對于本組數(shù)據(jù)的分析結(jié)果如圖3 ～5 所示。

圖3 隨機誤差相關(guān)性分析圖

圖4 隨機誤差PSD 分析

圖5 Allan 方差分析

從圖3 ～4 可以看到，隨機誤差自相關(guān)與互相關(guān)曲線都具有嚴重的拖尾現(xiàn)象，功率譜密度圖出現(xiàn)尖峰，這說明隨機誤差里含有周期性噪聲和有色噪聲;圖5 Allan 方差辨識結(jié)果也支持這一點結(jié)論，并且可以從圖上更細致地辨識各種誤差;數(shù)據(jù)中白噪聲范圍分布較廣，周期性噪聲集中在中高頻部分，有色噪聲一般集中在低頻部分，可能會與集中在低頻部分的有用信號混淆，很難從頻域角度對其進行分離［17－18］。總之，多種復雜的噪聲項使隨機誤差的建模非常繁瑣且制約其精度。

小波變換能平穩(wěn)化信號，基于小波多分辨的閥值去噪優(yōu)于基于傅立葉變換的傳統(tǒng)去噪方法。對角神經(jīng)網(wǎng)絡(luò)(DRNN)具有內(nèi)遞歸特性和局部反饋特性，動態(tài)性能優(yōu)于ARMA、前向神經(jīng)網(wǎng)絡(luò)，且節(jié)點少于全局反饋網(wǎng)絡(luò)，有更好的動態(tài)性和實時性。本文采用這兩種理論進行組合來處理陀螺隨機誤差并建模。首先對隨機誤差數(shù)據(jù)進行小波閥值去噪，濾除高頻噪聲;然后對去噪后的噪聲進行DRNN 建模，并進行預測。

利用小波去噪需要選取小波基函數(shù)和分解尺度，在這兩點確定后再進行閥值選取和量化。對于小波函數(shù)，綜合考量計算量和去噪效果，經(jīng)對比實驗后選取sym4 小波;在分解層次大于4 尺度后，高頻系數(shù)均值出現(xiàn)較大波動，所以選取分解尺度為4層。各層低頻、高頻系數(shù)如圖6 所示;采用軟閥值去噪，效果如圖7 所示，經(jīng)去噪后，陀螺隨機噪聲方差從0.008 8 降到6.59e-4，降噪效果明顯。

圖6 小波分解各層系數(shù)

圖7 小波去噪效果圖

小波變換具有非因果性，且不具有平移不變性，不能實現(xiàn)時間序列的遞推估計，這限制了小波去噪的在線應用。

從時間序列分析角度出發(fā)，研究對象的模型是非常有效的，大部分基于實驗數(shù)據(jù)的建模都是以此開展的。利用神經(jīng)網(wǎng)絡(luò)對時間序列數(shù)據(jù)進行建模已經(jīng)有不少的研究應用，其主要思想是仿照ARMA 模型方法進行非線性的建模［13］，具有延遲的外部遞歸神經(jīng)網(wǎng)絡(luò)非常好的體現(xiàn)了這一特點。對角遞歸神經(jīng)網(wǎng)絡(luò)作為具有延遲的內(nèi)遞歸神經(jīng)網(wǎng)絡(luò)，同外遞歸神經(jīng)網(wǎng)絡(luò)一樣可以實現(xiàn)時間序列建模、預報，且不需要事先知道模型的階次。小波去噪后，引入DRNN 對剩余的低頻噪聲進行建模，實現(xiàn)遞推是可實現(xiàn)的。

本文采用具有3 層結(jié)構(gòu)的DRNN，輸入層含兩個神經(jīng)元，兩個輸入分別為當前時刻值和當前時刻的估計值;輸出層含一個神經(jīng)元，網(wǎng)絡(luò)的輸出為下一時刻的估計值;隱層神經(jīng)元經(jīng)多次實驗后取15個。隱層神經(jīng)元傳遞函數(shù)為S 型函數(shù)，輸出神經(jīng)元傳遞函數(shù)為purelin 函數(shù)。取去噪后2 500 組數(shù)據(jù)，對前500 組數(shù)據(jù)進行神經(jīng)網(wǎng)絡(luò)訓練建模，后2 000 組數(shù)據(jù)進行驗證。神經(jīng)網(wǎng)絡(luò)訓練數(shù)據(jù)跟期望數(shù)據(jù)對比如圖8 所示，2 000 組預測效果如圖9 所示。

圖8 神經(jīng)網(wǎng)絡(luò)訓練效果

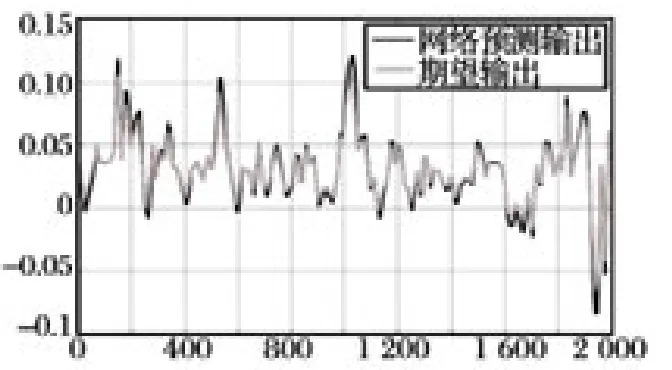
圖9 神經(jīng)網(wǎng)絡(luò)預測效果

圖8 中，低頻部分經(jīng)DRNN 建模采用LMBP 算法收斂速度非常快。從圖9 可以看到DRNN 泛化能力較好，所預測的輸出與期望的數(shù)值基本吻合。定量分析發(fā)現(xiàn)，DRNN 建模誤差均值為－0.002 5，方差為4.387 0e-4;利用DRNN 模型進行預測的誤差均值為－1.028 4e-4，方差為5.774 5e-5。并且經(jīng)殘差自相關(guān)與互相關(guān)分析發(fā)現(xiàn)，DRNN 模型的誤差和預測的誤差都為白噪聲過程。

4 結(jié) 論

針對光纖陀螺隨機誤差，本文組合采用小波閥值去噪和DRNN 的建模并仿真驗證。結(jié)果表明，采用這兩種方法組合處理光纖陀螺隨機誤差，能夠有效地對隨機誤差建模和補償，從而提高慣導系統(tǒng)的測量精度。但同時，小波去噪和DRNN 建模都存在實時性較差的問題，需進一步研究相對應的快速算法以應對工程應用。

［1］El－Sheimy N，Hou Haiying，Niu Xiaoji. Analysis and Modeling of Inertial Sensors Using Allan Variance［J］.IEEE Transaction on Instrumentation and Measurement，2008，57(1):140－149.

［2］李穎，陳興林. ARMA 模型辨識及其在光纖陀螺漂移建模中的應用［J］. 系統(tǒng)工程與電子技術(shù)，2008，30(9):1752－1754.

［3］盧海曦，夏敦柱，周百令. 基于遺傳小波神經(jīng)網(wǎng)絡(luò)的MEMS 陀螺誤差建模［J］. 中國慣性技術(shù)學報，2008，16(2):216－219.

［4］梁瑩，談?wù)穹瑥垜c，等. 一種光纖陀螺隨機漂移的高精度建模方法［J］. 哈爾濱工程大學學報，2009，30(11):1251－1255.

［5］谷政，江惠坤.非平穩(wěn)時間序列的小波混合方法及其應用［J］. 系統(tǒng)工程，2008，26(5):85－89.

［6］徐科，徐金梧.基于小波分解的某些非平穩(wěn)時間序列預測方法［J］. 電子學報，2001，29(4):566－568.

［7］高靜，李朝偉，董云峰，等. 空空導彈導引頭小波降噪?yún)?shù)優(yōu)選仿真研究［J］. 航空兵器，2010(5):48－54.

［8］李程，朱家海.基于小波和時間序列分析的陀螺隨機漂移建模研究［J］. 彈箭與制導學報，2005，25(4):402－404.

［9］謝聶，朱家海. 非平穩(wěn)時間序列的陀螺隨機漂移數(shù)據(jù)處理方法［J］. 空軍工程大學學報，2008，9(1):14－17.

［10］吳富梅，楊元喜.基于高階AR 模型的陀螺隨機漂移模型［J］. 測繪學報，2007，36(4):389－394.

［11］韓良軍. 光纖陀螺的誤差分析、建模及濾波研究［D］. 哈爾濱:哈爾濱工業(yè)大學，2008.

［12］張善文，雷英杰，馮有前. MATLAB 在時間序列分析中的應用［M］. 西安:西安電子科技大學出版社，2007.

［13］王科俊，王克成. 神經(jīng)網(wǎng)絡(luò)建模、預報與控制［M］. 哈爾濱:哈爾濱工程大學出版社，1996.

［14］Hagan M T，Demuth H B. 神經(jīng)網(wǎng)絡(luò)設(shè)計［M］. 戴葵，譯. 北京:機械工業(yè)出版社，2002.

［15］毛奔，林玉榮. 慣性器件測試與建模［M］. 哈爾濱:哈爾濱工程大學出版社，2007.

［16］Hou Haiying. Modeling Inertial Sensors Errors Using Allan Variance［D］. Alberta:University of Calgary，2004.

［17］Nassar S，Schwarz K P，EI－Sheimy N. Modeling Inertial Sensor Errors Using Autoregressive (AR)Models［J］. Navigation，2004，51(24):259－268.

［18］Liu Luyuan，Chen Yuzhu，Chen Gang，et al. Model and Experiment Research on Gyro Drift Rate Based on Wavelet Transform［J］. Journal of Chinese Inertial Technology，2004，12(1):61－65.