最近鄰演化網絡模型
徐玉章
最近鄰演化網絡模型
徐玉章

江蘇省自然科學基金項目:BK20141071
徐玉章 朱 磊
中國人民解放軍理工大學通信工程學院
我們生活在一個充滿復雜系統的社會中,其中很多系統的結構都可以用復雜網絡來刻畫。20世紀末,科學家們建立了兩個重要的復雜網絡模型。其中一個模型是WS小世界網絡模型,該模型融合了規則網絡的大聚類特性和隨機圖網絡平均路徑長度較小的特性,可以說,WS小世界網絡模型是一種介于規則網絡和完全隨機網絡之間的網絡模型。但隨著復雜網絡研究的深入,人們發現越來越多的真實生活中的網絡呈現出無標度(節點的度即與節點相連的邊的數量)的特點,即網絡中節點的度服從冪律分布,在雙對數坐標下是一條斜線,而不是單峰曲線,另一種重要的復雜網絡模型應運而生。1999年,Barabási和Albert成功地提出了BA無標度網絡模型,他們在該模型中解釋了復雜網絡無標度性質的一種可能形成機制:增長和隨機連接。BA無標度網絡模型被認為是最著名的復雜網絡模型之一。
在以往的復雜網絡模型的研究中很少考慮區域和距離的因素。然而,很多真實的網絡受限于節點的位置和節點間的距離,例如,現代物流網絡和大型集會中的臨時通信網絡,人際關系網絡中也有區域的限制。假設存在若干區域,每塊區域中有一個“骨干節點”。每個骨干節點和其鄰近的骨干節點相連,新加入的節點選擇其附近的節點進行連接。節點代表了通信節點、物流中心等實際場景,邊代表了節點之間的聯系。在這種情況下,節點和邊的連接遵循就近原則,即節點更傾向于與最近的鄰居相連。上述情況在我們的生活中幾乎時時刻刻都在發生,我們該如何構建與之相符的模型來描述這種情況呢?如何得出模型的關鍵指標?新模型將具有哪些特性?為此,本文提出了“最近鄰演化網絡模型”。
1 最近鄰演化網絡模型的構建
本文在BA無標度網絡的構建算法的基礎上引入區域和距離的限制,鄰近的節點將會位于同一簇中。最近鄰演化網絡模型的構建算法如下。
(1)初始狀態:具有m0個節點的最近鄰耦合網絡。每個節點和鄰近的左右兩側各K/2(K為偶數)個節點相連,稱這m0個初始節點為“骨干節點”。
(2)歸屬節點和節點簇:當一個新節點加入網絡后,距該節點最近(距離以邊數衡量,最近即最短路徑上的邊數最少)的骨干節點稱為該節點的“歸屬節點”(如果幾個骨干節點與新節點的距離相同且均是最少,則從中隨機選取一個作為節點i的歸屬節點)。具有同一歸屬節點的節點構成一個“節點簇”。
(3)增長:每次只允許一個節點加入網絡。新節點加入時,首先選擇2個相鄰的節點簇,再從這兩個節點簇中選擇m(m>=2)個節點進行連接。(在初始階段,節點簇中的節點數一般會小于m,所以規定新加入的節點只和其選擇的節點簇中2個節點連接)
(4)優先連接:新節點在選擇節點進行連接時,采用優先連接的機制,即新節點和節點i相連的概率與節點i的度ki有關,度越大,連接概率越大,按如下公式計算:

其中,Pclusters表示選擇的節點簇中包含節點i的概率,

2 最近鄰演化網絡模型的基本指標
復雜網絡研究中刻畫網絡特性的三個基本指標為:度分布、聚類系數和平均路徑長度。度分布指網絡中節點度的分布,節點的度(如前述,即與該節點相連的邊的數目)可以衡量一個節點的重要程度,充分了解網絡的度分布,可以使我們對網絡拓撲有一個直觀的把握,并進一步幫助人們更深入地了解復雜系統。聚類系數是衡量網絡中鄰近節點聯系緊密程度的指標,網絡的聚類特性在某種程度上可以概括為社會關系網絡中“物以類聚,人以群分”的特性。平均路徑長度可用來衡量網絡中節點間距離的大小,如果網絡的平均路徑長度的增加速度至多與網絡規模的對數成正比,就說這個網絡具有小世界效應。
度分布
將公式(2)帶入公式(1)得到

長時間后,每個節點簇中的節點數將遠大于m,所以公式(3)中的約等于號成立。
利用主方程法,得到穩態度分布為:
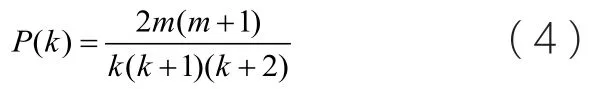
該公式表明最近鄰演化網絡模型和BA無標度網絡模型具有相同的度分布。實驗結果和理論值吻合地較好。雙對數坐標系下的斜線表明該網絡在具有眾多小度數節點的同時,仍在存在少量的大度節點,這也是網絡增長過程中擇優連接的一個必然產物。
聚類系數
聚類系數指節點i的ki個鄰居節點之間實際存在的連邊數Ei與這ki節點所有可能的連邊數目之比,衡量了網絡中鄰近節點間的緊密程度,用Ci表示,即

這里“i”既是節點的代號,又是節點加入網絡的時間點。利用平均場理論,得到最近鄰演化網絡的聚類系數(隨時間變化)為:
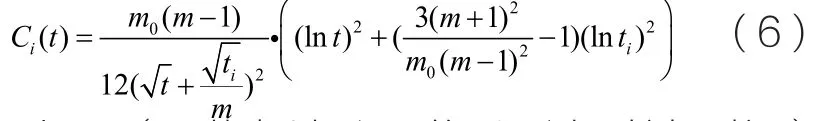
當ti遠小于t(即節點i加入網絡后又過了較長時間)時,Ci(t)可作如下近似,

平均路徑長度
網絡中兩節點i和j之間的距離dij定義為連接這兩個節點的最短路徑的邊數。網絡的平均路徑長度L定義為任意兩個節點之間的距離的平均值,即
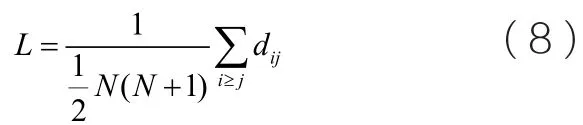
其中N為網絡節點個數,因為每一時刻網絡中有且只有一個節點加入,所以若不考慮網絡的初始規模,該處的N等價于t。
給出了無標度網絡平均路徑長度的尺度,

如表1所示,通過仿真,本文得到了最近鄰演化網絡的平均路徑長度L,L的增長速度介于公式(9)和lnN之間。隨網絡規模的增加,平均路徑長度的增長十分緩慢,表明該網絡具有較明顯的“小世界效應”。

表1 最近鄰演化網絡模型的平均路徑長度
3 總結與展望
現實生活中很多網絡與區域和距離因素息息相關,而以往的復雜網絡模型對區域和距離的因素考慮較少。本文將區域的概念引入無標度網絡,建立了最近鄰演化網絡模型,并深入分析了該模型的度分布、聚類系數和平均路徑長度。結果表明,最近鄰演化網絡模型具有與BA無標度網絡相同的度分布,此外,在保持較小的平均路徑長度的同時,該模型顯示出更好的聚類特性,即鄰近節點間的聯系更加緊密。下一步,我們將進一步探究該模型的抗毀性。此外,在無標度網絡的構建中,人們專注于擇優連接以求獲得無標度特性,忽略了隨機連邊對網絡特性的影響,在復雜網絡模型研究中引入隨機連邊機制也將具有潛在重要意義。
10.3969/j.issn.1001-8972.2015.02.050