旋轉(zhuǎn)彈體及減旋片滾轉(zhuǎn)阻尼數(shù)值模擬

趙養(yǎng)正，蔣勝矩，黨明利，朱中根

（西安現(xiàn)代控制技術(shù)研究所，陜西西安710065）

旋轉(zhuǎn)彈體及減旋片滾轉(zhuǎn)阻尼數(shù)值模擬

趙養(yǎng)正，蔣勝矩，黨明利，朱中根

（西安現(xiàn)代控制技術(shù)研究所，陜西西安710065）

滾轉(zhuǎn)阻尼力矩導(dǎo)數(shù)是影響減旋效果的重要參數(shù)。采用求解定常流場(chǎng)的計(jì)算流體力學(xué)方法，對(duì)亞跨聲速階段帶減旋片翼翼身組合體的滾轉(zhuǎn)阻尼特性進(jìn)行數(shù)值模擬。滾轉(zhuǎn)阻尼力矩導(dǎo)數(shù)數(shù)值模擬的結(jié)果與試驗(yàn)值一致性較好。通過數(shù)值結(jié)果分析解釋了由于滾轉(zhuǎn)引起的彈翼氣流攻角的變化，表面壓力的變化，以及附加升力導(dǎo)致的滾轉(zhuǎn)阻尼力矩的形成原因，展示了薄翼片彎折的位置，同時(shí)從流場(chǎng)的角度展示了滾轉(zhuǎn)對(duì)彈體附近氣體流動(dòng)的影響，以及滾轉(zhuǎn)引起的表面流線的彎曲，螺旋狀尾跡。

兵器科學(xué)與技術(shù)；滾轉(zhuǎn)阻尼導(dǎo)數(shù)；彈體；減旋片；數(shù)值模擬

0 引言

炮射末敏子彈藥在從母彈分離出來(lái)時(shí)具有較高的轉(zhuǎn)速，為了滿足末端尋的要求，需要將高速旋轉(zhuǎn)的彈體迅速降至所要求的轉(zhuǎn)速，矩形減旋片以其簡(jiǎn)單的形狀常常被作為氣動(dòng)減旋部件使用，其滾轉(zhuǎn)阻尼力矩（極阻尼力矩）系數(shù)導(dǎo)數(shù)是衡量減旋效果的重要參數(shù)，為了獲得這一參數(shù)并指導(dǎo)設(shè)計(jì)，過去常常采用工程估算的方法，但是對(duì)鈍頭體精度較差，目前采用數(shù)值方法計(jì)算復(fù)雜外形和非常規(guī)外形的動(dòng)態(tài)導(dǎo)數(shù)替代風(fēng)洞試驗(yàn)和工程計(jì)算已成趨勢(shì)，文獻(xiàn)［1］對(duì)帶矩形翼的平頭旋轉(zhuǎn)體的滾轉(zhuǎn)阻尼力矩系數(shù)進(jìn)行了試驗(yàn)研究，文獻(xiàn)［2］對(duì)飛機(jī)標(biāo)模的動(dòng)導(dǎo)數(shù)進(jìn)行了試驗(yàn)研究，尤其是大攻角狀態(tài)下的動(dòng)導(dǎo)數(shù)，均得到了很好的結(jié)果，但是動(dòng)態(tài)試驗(yàn)對(duì)高速旋轉(zhuǎn)驅(qū)動(dòng)設(shè)備的調(diào)試、數(shù)據(jù)采集和處理技術(shù)要求很高，同時(shí)試驗(yàn)費(fèi)用大，周期長(zhǎng)；相對(duì)試驗(yàn)的方法求解動(dòng)導(dǎo)數(shù)，數(shù)值方法簡(jiǎn)單費(fèi)用低，精度能夠滿足工程要求，逐漸成為研究熱點(diǎn)，文獻(xiàn)［3］采用求解定常流場(chǎng)的方法對(duì)格柵翼導(dǎo)彈的滾轉(zhuǎn)阻尼導(dǎo)數(shù)進(jìn)行了計(jì)算分析，文獻(xiàn)［4-5］分別采用定常數(shù)值計(jì)算的方法計(jì)算了動(dòng)導(dǎo)數(shù)，但在可用的文獻(xiàn)中，采用數(shù)值方法對(duì)帶減旋片的平頭圓柱體的滾轉(zhuǎn)阻尼導(dǎo)數(shù)進(jìn)行研究沒有涉及。在設(shè)計(jì)的初級(jí)階段采用試驗(yàn)的方法費(fèi)用昂貴，因此通過數(shù)值模擬的方法解算帶減旋片的滾轉(zhuǎn)彈體的流場(chǎng)，從而獲得較好精度的滾轉(zhuǎn)阻尼力矩系數(shù)導(dǎo)數(shù)就顯得非常必要。

1 模型及幾何參數(shù)

模型結(jié)構(gòu)為平頭園柱體+4片矩形彈翼，具體如圖1所示，其模型參數(shù)見表1，其中L表示彈長(zhǎng)，D表示彈徑，s表示彈翼展長(zhǎng)，C表示彈翼弦長(zhǎng)。

圖1 模型幾何尺寸簡(jiǎn)圖Fig.1 Model geometry

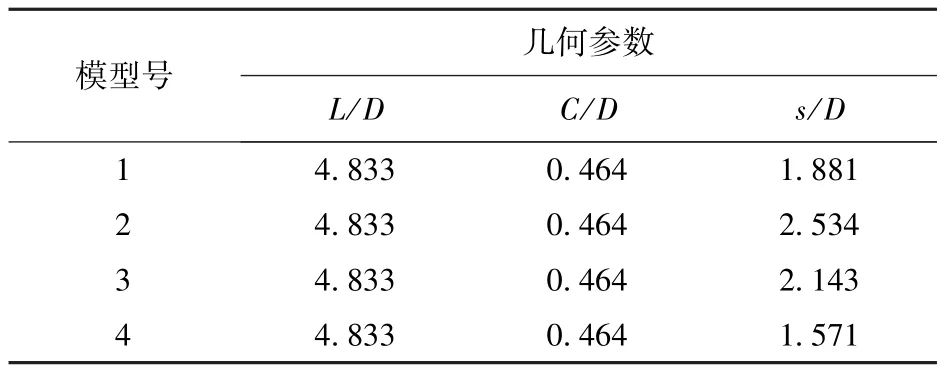
表1 模型參數(shù)Tab.1 Parameters of model

2 數(shù)值方法

2.1 計(jì)算方法

由于模型是旋轉(zhuǎn)的，為了將問題轉(zhuǎn)化為定常流動(dòng)問題，計(jì)算中采用了旋轉(zhuǎn)坐標(biāo)系，并將坐標(biāo)系固定在旋轉(zhuǎn)模型上，從這個(gè)坐標(biāo)系觀察模型是靜止的，而流場(chǎng)是轉(zhuǎn)動(dòng)的，因此在旋轉(zhuǎn)坐標(biāo)系下，方程中增加了離心力和科里奧利力的影響。

2.1.1 旋轉(zhuǎn)坐標(biāo)系下的Navier-Stokes方程

SST湍流模型見CFX軟件有關(guān)說明。

文中使用計(jì)算流體力學(xué)軟件CFX進(jìn)行數(shù)值計(jì)算。具體數(shù)值解算方法為:采用有限體積法離散控制方程，對(duì)流項(xiàng)采用基于有界性原理的高分辨率格式，湍流方程的離散格式為迎風(fēng)格式，時(shí)間項(xiàng)采用隱式時(shí)間離散格式。由于模型是旋轉(zhuǎn)的，因此采用了動(dòng)靜兩個(gè)計(jì)算域來(lái)處理，動(dòng)域給定某一轉(zhuǎn)速繞轉(zhuǎn)軸旋轉(zhuǎn)，靜域?yàn)殪o止的，動(dòng)靜域之間的數(shù)據(jù)交換通過交界面進(jìn)行，采用凍結(jié)轉(zhuǎn)子模型。

邊界條件:入口邊界采用來(lái)流速度和溫度；出口邊界采用靜壓和溫度；遠(yuǎn)場(chǎng)邊界采用無(wú)粘滑移邊界墻；壁面邊界采用無(wú)滑移壁面條件，并設(shè)定壁面旋轉(zhuǎn)轉(zhuǎn)速為0 r/s.

2.1.2 滾轉(zhuǎn)阻尼導(dǎo)數(shù)計(jì)算公式

式中:（mx）ωx是由ωx引起的滾轉(zhuǎn)力矩系數(shù)；

2.2 計(jì)算網(wǎng)格

整個(gè)彈體網(wǎng)格分為內(nèi)外兩個(gè)域，內(nèi)域?yàn)樾D(zhuǎn)域，外域?yàn)殪o止域，內(nèi)外域之間具有圓柱交接面，附面層計(jì)算網(wǎng)格采用三棱柱形，Y+小于50，外場(chǎng)采用四面體網(wǎng)格。入口距彈頭為8L，出口距彈底10L，側(cè)面外場(chǎng)距彈軸5D，如圖2所示。模型的表面網(wǎng)格和附面層網(wǎng)格如圖3和圖4所示。

2.3 計(jì)算條件

馬赫數(shù)Ma:0.4、0.5、0.6、0.7、0.8、0.9；攻角: 0°；轉(zhuǎn)速:50 r/s、100 r/s、180 r/s.

3 結(jié)果與討論

本次數(shù)值計(jì)算是通過對(duì)零攻角，3種轉(zhuǎn)速下平頭圓柱+4片矩形翼模型的滾轉(zhuǎn)力矩系數(shù)進(jìn)行了解算，圖5為馬赫數(shù)Ma為0.4時(shí)滾轉(zhuǎn)力矩系數(shù)mx對(duì)無(wú)量綱滾轉(zhuǎn)角速度的變化曲線，從圖5可以看出，線性度很好，通過求解曲線斜率可以獲得滾轉(zhuǎn)阻尼導(dǎo)數(shù)值。圖6為滾轉(zhuǎn)阻尼導(dǎo)數(shù)的計(jì)算值和風(fēng)洞試驗(yàn)結(jié)果的對(duì)照曲線。為了驗(yàn)證計(jì)算的正確性，采用自由滾轉(zhuǎn)技術(shù)，分別在風(fēng)洞吹風(fēng)狀態(tài)和不吹風(fēng)狀態(tài)驅(qū)動(dòng)模型旋轉(zhuǎn)達(dá)到某一轉(zhuǎn)速，然后脫開驅(qū)動(dòng)裝置，測(cè)量轉(zhuǎn)速隨時(shí)間變化，并按照文獻(xiàn)［1］的方法計(jì)算獲得模型的滾轉(zhuǎn)阻尼力矩系數(shù)導(dǎo)數(shù)。試驗(yàn)條件:馬赫數(shù)和攻角與計(jì)算相同；驅(qū)動(dòng)裝置脫開時(shí)轉(zhuǎn)速: 60 r/s、110 r/s、190 r/s；試驗(yàn)與計(jì)算模型尺寸相同。從圖6中可以看出滾轉(zhuǎn)阻尼導(dǎo)數(shù)的計(jì)算與試驗(yàn)結(jié)果的變化趨勢(shì)非常一致，模型1和模型4計(jì)算值和試驗(yàn)值較為接近，誤差為7%，模型3計(jì)算值與試驗(yàn)值差11%，模型2計(jì)算值與試驗(yàn)值差距稍大，接近17%，可能是翼片附面層網(wǎng)格較少，當(dāng)翼片展長(zhǎng)增加后，翼片稍部局部高壓區(qū)進(jìn)一步增大，流場(chǎng)計(jì)算對(duì)這一高壓區(qū)捕捉不夠準(zhǔn)確造成的，見圖4，同時(shí)試驗(yàn)本身也存在誤差。從圖6中還可以看出，隨著馬赫數(shù)的增加，滾轉(zhuǎn)阻尼逐漸減小；隨著翼片展長(zhǎng)的增加（次序?yàn)槟Ｐ?、模型1、模型3、模型2），滾轉(zhuǎn)阻尼逐漸增大。從圖7可以看出，隨著無(wú)量綱展長(zhǎng)s/D的增加，顯著增加，二者基本呈線性關(guān)系，不同馬赫數(shù)下均有類似結(jié)果。圖8為尾部截面的速度矢量圖，從圖中可以看出在模型繞自身軸線轉(zhuǎn)動(dòng)時(shí)，翼片攪動(dòng)了周圍的流場(chǎng)，附近的氣流也隨著彈體一起轉(zhuǎn)動(dòng)，在臨近的翼片和彈體之間，存在著明顯的流渦，流速較低。

圖2 計(jì)算域示意圖Fig.2 Computing domain

圖3 表面網(wǎng)格及附面層網(wǎng)格Fig.3 Surface mesh and boundary layer mesh

圖4 翼片表面壓力分布Fig.4 Contours of static pressure on wings

圖5 滾轉(zhuǎn)力矩系數(shù)隨無(wú)量綱滾轉(zhuǎn)角速度的變化曲線Fig.5 Variation of rolling-moment coefficient withspin rate parameter

圖6 滾轉(zhuǎn)阻尼導(dǎo)數(shù)隨馬赫數(shù)的變化曲線Fig.6 Variation of roll-damping coefficientwith Mach number

圖7 展長(zhǎng)對(duì)滾轉(zhuǎn)阻尼導(dǎo)數(shù)的影響Fig.7 Effect of span on roll-damping derivative

圖8 尾部截面速度矢量圖（從頭部看，Ma=0.9）Fig.8 Velocity vectors at the tail section（viewing from head，Ma=0.9）

從圖9左右翼對(duì)稱剖面的矢量圖可以看出，左翼的當(dāng)?shù)毓ソ菫檎乙淼漠?dāng)?shù)毓ソ菫樨?fù)，而且左右翼產(chǎn)生了大小相等，方向相反的附加升力，這是因?yàn)楫?dāng)彈體繞其縱軸轉(zhuǎn)動(dòng)時(shí)，使彈翼的每一個(gè)剖面產(chǎn)生附加的垂直速度，對(duì)左、右翼來(lái)說該垂直速度大小相等，方向相反，每個(gè)翼上的垂直速度與來(lái)流速度合成一個(gè)速度矢量，而左右翼上的合成速度與彈軸的夾角正好相反，形成了方向相反的附加攻角，產(chǎn)生方向相反的附加升力；同時(shí)從圖10也可以看出，當(dāng)零攻角時(shí)，由于模型旋轉(zhuǎn)，翼片的左面（沿左旋方向看）附近壓力較高，右面壓力較低，引起了翼片左右面附近形成壓力差，但對(duì)對(duì)稱模型零攻角時(shí)，如果沒有旋轉(zhuǎn)，彈翼左右面壓力應(yīng)相同，不會(huì)產(chǎn)生這一壓力差。由于模型旋轉(zhuǎn)產(chǎn)生的這個(gè)壓力差會(huì)形成附加升力，而且彈體左右邊和上下邊彈翼的這一壓力差成對(duì)反向，因此翼片上的附加升力也成對(duì)反向，并且每個(gè)彈翼上的附加升力均與彈體滾轉(zhuǎn)方向相反，這就是滾轉(zhuǎn)阻尼力矩產(chǎn)生的緣由。圖11為翼片表面力的分布，翼片所受總力是與壓力差相關(guān)的，與圖12的翼片表面壓力分布一致。在實(shí)際的試驗(yàn)中由于翼片較薄也遇到了翼片在高壓的翼梢三角區(qū)向滾轉(zhuǎn)方向相反的方向彎折的現(xiàn)象。

圖9 左右彈翼對(duì)稱截面速度矢量圖（Ma=0.9）Fig.9 Velocity vectors at symmertrical sections of left and right wings（Ma=0.9）

圖10 彈翼壓力云圖（從頭部看，Ma=0.9）Fig.10 Contour of static pressure on wings（viewing from head，Ma=0.9）

圖11 翼片表面力分布Fig.11 Distribution of force on wing surfaces

圖13和圖14分別為彈體表面流線圖及頭部和翼片流線圖，可以看出由于彈體的滾轉(zhuǎn)引起了表面流線的彎曲，也使頭部和翼片尾跡流線呈螺旋狀。圖15為彈體縱向截面馬赫數(shù)云圖，由于為平頭體，因此在頭部就出現(xiàn)了較大的流動(dòng)分離，并且該分離流改變了翼片附近的流場(chǎng)，從尾跡看由滾轉(zhuǎn)引起的流動(dòng)分離也較大。

圖12 彈體表面壓力云圖Fig.12 Contour of static pressure on body surface

圖13 模型表面流線圖Fig.13 Streamline of model surface

圖14 頭部和翼片流線圖Fig.14 Streamline of head and wings

圖15 彈體縱向截面馬赫數(shù)云圖（Ma=0.9）Fig.15 Contour of Mach number at the longitudinal section（Ma=0.9）

4 結(jié)論

本文通過數(shù)值計(jì)算研究了滾轉(zhuǎn)阻尼導(dǎo)數(shù)的計(jì)算方法，并通過與試驗(yàn)結(jié)果對(duì)比分析得出如下結(jié)論:

1）本文采用的數(shù)值方法計(jì)算滾轉(zhuǎn)阻尼導(dǎo)數(shù)實(shí)用、可靠，與試驗(yàn)結(jié)果一致性好。

2）隨著馬赫數(shù)的增加，滾轉(zhuǎn)阻尼逐漸減小。

3）隨著展長(zhǎng)的增加，滾轉(zhuǎn)阻尼增大。

4）采用數(shù)值方法可以直觀地看出滾轉(zhuǎn)阻尼力矩產(chǎn)生的流動(dòng)機(jī)理。

5）當(dāng)翼片較薄時(shí)，可以采用此方法預(yù)估翼片彎曲的位置。

6）通過計(jì)算獲得的螺旋形尾跡，使研究者更進(jìn)一步了解到滾轉(zhuǎn)運(yùn)動(dòng)對(duì)流場(chǎng)的影響。

（

）

［1］ 丁則勝，劉亞飛，徐琴，等.彈體及減旋片滾轉(zhuǎn)阻尼實(shí)驗(yàn)研究［J］.彈道學(xué)報(bào)，2001，13（1）:62-65. DING Ze-sheng，LIU Ya-fei，XU Qin，et al.Roll damping experimental study of body and anti-rotation flaps［J］.Journal of Bollistics，2001，13（1）:62-65.（in Chinese）

［2］ 趙忠良，任斌.1.2 mm風(fēng)洞大攻角動(dòng)導(dǎo)數(shù)試驗(yàn)技術(shù)［J］.流體力學(xué)實(shí)驗(yàn)與測(cè)量，1998，12（1）:56-61. ZHAO Zhong-liang，REN Bin.High angle of attack dynamic derivatives experiment technique in 1.2 mm wind tunnel［J］.Experiments and Measurements in Fluid Mechanics，1998，12（1）:56-61.（in Chinese）

［3］ 鄧帆，陳少松，陶鋼.帶柵格翼導(dǎo)彈超聲速階段滾轉(zhuǎn)阻尼導(dǎo)數(shù)的數(shù)值研究.［J］.空氣動(dòng)力學(xué)學(xué)報(bào)，2012，30（2）:151-156. DENG Fan，CHEN Shao-song.TAO Gang.CFD analysis of roll damping derivatives for missile with grid fins at supersonic speeds［J］.Acta Aerodynamica Sinica，2012，30（2）:151-156.（in Chinese）

［4］ Mechael A P，Lawrence L G.Steady-state computation of constant rotational rate dynamic stability derivatives，AIAA 2000-4321［R］.Washington，DC:George Washington University，2000.

［5］ Despirito J，Silton S I，Weinacht P.Navier-Stokes predictions of dynamic stability derivatives-evaluation of steady-state methods，ARL-TR-4605［R］.Maryland，US:ARL，2008.

Roll Damping Simulation of Missile Body and Anti-rotation Flaps

ZHAO Yang-zheng，JIANG Sheng-ju，DANG Ming-li，ZHU Zhong-gen
（Xi'an Modern Control Technology Research Institute，Xi'an 710065，Shaanxi，China）

Roll damping derivative is an important aerodynamic parameter which affects the despinning effect of a missile.Steady CFD simulations are used to predict the roll damping characteristics of the missile with anti-rotation flaps at subsonic and transonic speeds.The predicted roll damping derivatives are in good agreement with the experimental data.The variation of the angle of attack and the surface pressure of wings due to rolling and the roll damping moment induced by additional wing lift are explained through numerical analysis.The bending location of the thin wings is shown.From the view of flow field，the influence of spinning on gas flow nearby the body of missile，the bending of surface streamline and the helical-like streamline pattern in the wake are demonstrated.

ordnance science and technology；roll damping derivative；missile body；anti-rotation flap；numerical simulation

V211.3

A

1000-1093（2015）07-1176-05

10.3969/j.issn.1000-1093.2015.07.004

2014-08-14

趙養(yǎng)正（1965—），男，高級(jí)工程師。E-mail:jie_lan2000@sina.com.cn