(g'/g2)展開法及其在KPP方程中的應用

孫 鵬，崔澤建

(西華師范大學 數學與信息學院，四川 南充 637009)

非線性發展方程可以用來描述自然科學和應用科學的許多復雜現象．尋找新的求解方法并得到非線性發展方程的新形式精確解，作為非線性發展方程的重要研究內容已經成為該領域的研究熱點之一．

近年來，許多簡單有效的求解方法已經被提出并發展起來，例如Tanh-展開法［1］、F-展開法［2］、齊次平衡法［3］、指數展開法［4］、雅克比橢圓函數法［5］、Hirota 雙線性展開法［6］和(G'/G)展開法［7］等．

受(G'/G)展開法的啟發，LI［8］等提出了(ω/g)展開法．(G'/G)和(g'/g2)作為(ω/g)展開法的兩種特殊方法已被運用于求解Vakhnenko 方程，結果表明相比于(G'/G)展開法，(g'/g2)展開法在過程中更加簡單方便．黃［9］等運用(G'/G)展開法求解了KPP 方程，陳［10］等運用(g'/g2)展開法求解了CNKGE，本文將運用(g'/g2)展開法求解KPP 方程．

1 (g'/g2)展開法

非線性方程的一般形式可表示為:

把未知函數u=u(x，t)作行波變換，得u=u(ξ)，ξ=x-Vt，然后將方程(1)化作關于變量ξ 的常微分方程:

(g'/g2)展開法是假設方程(2)的解可以表示成一個如下多項式的形式:

其中g=g(ξ)滿足如下的二階常微分方程(ODE):

式(3)和(4)中ai(i=1，2，3，…，n)以及λ，μ 都是待定常數，且a0≠0，正整數n 由齊次平衡法確定．由方程(4)可得:

當μλ ＞0 時，

當μλ ＜0 時，

當μ=0，λ≠0 時，

其中c1和c2是任意常數．

u(ξ)可以利用以下步驟確定:

①利用齊次平衡法確定多項式(3)中的階數，從而確定解的形式．

②將(3)帶入(1)中，利用并且將(4)進行變形之后，得到新形式方程，再令其各項系數為0，確定系數ai．

③通過計算得出系數，最終確定解．

2 用(g'/g2)展開法解KPP 方程

KPP 方程的一般形式為:

令u=u(ξ)，ξ=x-Vt，那么ut= -Vu，uxx=u″，其中，u'是u 關于ξ 的一階導數，u″是u 關于ξ 的二階導數．那么此方程就變成如下形式:

由齊次平衡法得，O(n″)=n+2，O(n3)=3n，n+2 =3n，可得n=1．

因此

將上面幾式代入(9):

整理，合并同類項，令各項系數為0，得到:

an≠0 可得

(當a0，a1，取某一組值時，V 的值唯一)共得四組系數．

下面以其中任意一組系數說明(其他三組同理可得):

當λμ ＞0 時，得到三角函數通解

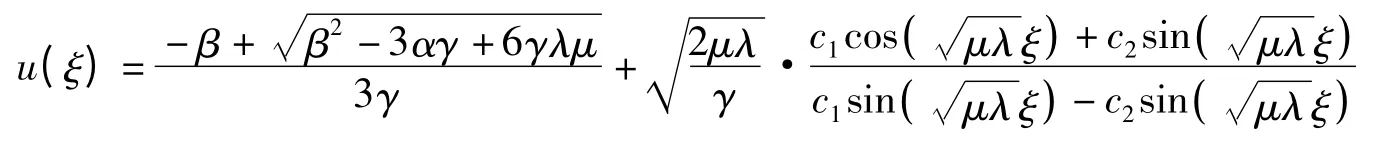
當λμ ＜0 時，得到雙曲函數通解

當μ=0，λ≠0 時，得到有理函數通解

其中c1和c2是任意常數．

3 結 論

本文通過運用(g'/g2)展開法成功求出KPP 方程的精確解，分為三類:三角函數通解，雙曲函數通解，有理函數通解．從求解的過程來看，(g'/g2)展開法直接有效，而且可以運用計算機進行求解，更為方便．因此，該方法可用于構造數學物理學中其他非線性發展方程的解．

［1］ FAN E G． Extended tanh-function method and its applications to nonlinear equations［J］． Phys Lett A，2000，277(4 -5):212-218．

［2］ ZHOU Y B，WANG M L，WANG Y L． Periodic wave solutions to a coupled KdV equations with variable coefficients［J］． Phys Lett A，2003，308(1):31 -36．

［3］ WANG M L． Solitary wave solutions for variant Boussinesq equations［J］． Phys Lett A，1995，199(3):169 -172

［4］ HE J H，ABDOU M A． New periodic solutions for nonlinear evolution equations using Exp-function method［J］．Chaos，Solitons and Fractals，2007，34(5):1421 -1429．

［5］ LIU S K，FU Z T，LIU S D，et al． Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations［J］． Phys Lett A，2001，289(S1 -2):69 -74．

［6］ HIROTA R． Exact solution of the Korteweg-de vries equation for multiple collisions of solitons［J］． Phys Rev Lett，1971，27(18):1192 -1194．

［7］ WANG M L，LIA X Z，ZHANG J L． The (G'/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics［J］． Phys Lett A，2008，372(4):417 -423．

［8］ LI W A，CHEN H，ZHANG G C． The (ω/g)-expansion method and its application to Vakhnenko equation［J］． Chinese Phys B，2009，18(2):400 -404．

［9］ 黃 怡，崔澤建． (G'/G)展開法和KPP 方程的新精確解［J］． 西華師范大學學報(自然科學版)，2013，34(2):199 -202．

［10］ 陳繼培，陳 浩． (g'/g2)展開法及其在耦合非線性Klein-Gordon 方程中的應用［J］．華南師范大學學報(自然科學版)，2012，44(2):63 -66．