大涵道比發動機渦輪過渡段氣動改型設計

郭澤潤，蔣首民，孔慶國，周 琨

（1.中國航天科工集團31研究所高超聲速沖壓發動機技術重點實驗室，北京100074；2.北京航空航天大學能源與動力工程學院，北京100191）

0 引言

隨著大涵道比發動機的發展，高、低壓渦輪間的徑向尺寸差逐漸增大，同時為了減輕渦輪風扇發動機的質量還要求過渡段的軸向尺寸盡可能小，導致目前過渡段的擴張角不斷增大。作為連接高、低壓渦輪的過渡部件，過渡段的設計自由度很低，根據上游高壓渦輪確定過渡段的進口尺寸和氣動條件，根據低壓渦輪確定其出口尺寸。低壓渦輪還會對過渡段出口的流場品質提出要求，例如降低過渡段出口馬赫數和較均勻的出口流場。這些限制條件很大程度上增加了過渡段的氣動設計難度。鄒正平等[1]指出過渡段內部復雜流動機理優化過渡段設計對提高渦輪性能有重要作用；文獻[2-8]討論了上游靜子的尾跡、氣流角、支板等對過渡段內流動的影響；Marn等[9]通過試驗和數值手段研究了高壓渦輪轉子出口氣流角、尾跡對過渡段性能的重大影響。上述研究說明過渡段的設計必須依據設計點的進口氣動條件進行。文獻[10]通過調整流線曲率的方式優化了原型過渡段的性能；Wallin等[11]通過對過渡段流道面積分布規律的優化設計減小了過渡段內總壓損失；孫志剛等[12]優化了某型燃氣輪機渦輪過渡段的子午流道，認為沿流向的面積分布規律是過渡段優化的1個重要方向。

本文依據過渡段設計的特點，提出了過渡段設計的5個步驟，對某大涵道比發動機的過渡段進行氣動設計，并且對原型進行3維改型優化。

1 過渡段設計流程

過渡段的幾何描述如圖1所示。按照文獻[13]所述，在不考慮過渡段輪轂和機匣流道的情況下，用于描述過渡段進、出口幾何的參數共有7個。將這7個參數無量綱化后得出3個無量綱參數：πAR、Lx/h1、Θ。πAR定義為過渡段出口面積除以進口面積，表征過渡段進、出口之間的壓力差；Lx/h1表征過渡段的無量綱長度；坡角Θ 表征過渡段內氣流平均爬升角度。

過渡段的氣動設計是1個反復迭代的過程（如圖2所示），一般包括5個步驟：幾何參數選取、進口氣動條件分析、支板葉型設計、流道型線設計和3維氣動性能校核。設計時應對這5個步驟反復迭代，尋求最佳的設計方案。

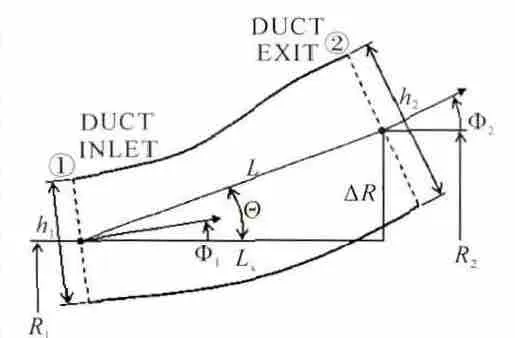
圖1 過渡段幾何描述

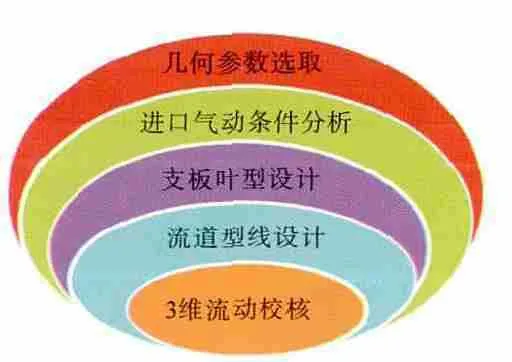
圖2 過渡段設計流程

1.1 總體幾何參數選取

首先依據發動機的總體方案和高、低壓渦輪對過渡段幾何尺寸，即進口幾何尺寸、流道傾角以及出口尺寸、流道傾角的要求計算出過渡段進、出口的面積比πAR和高、低壓渦輪之間的徑向尺寸差；通過發動機總體方案確定出過渡段軸向長度的尺寸范圍，選取1個合適的軸向長度，可以計算過渡段的長高比L/h1和爬升角Θ。根據幾何參數與流動分離的經驗關系[3]可初步判斷有無流動分離的危險，若有則應該考慮重新選擇幾何參數。

1.2 進口氣動條件分析

氣動條件包括過渡段進口邊界條件和過渡段出口氣動條件。過渡段的目的是為低壓渦輪進口提高穩定的高品質的流場，在設計過渡段流道和支板時必須提前考慮低壓渦輪進口氣動條件的特殊性，如過渡段出口馬赫數、氣流角沿徑向分布、支板的周向時序位置等。

1.3 支板葉片造型

通過1.1和1.2的步驟基本能確定設計點過渡段進口馬赫數的范圍，選擇在該馬赫數下表現不錯的NACA葉型作為原始葉型進行設計。根據支板最大厚度的要求以及所選葉型最大厚度與弦長比例，給出合適的支板弦長（考慮過渡段軸向長度）。支板內部需要通過液壓和控制管路，因此必須采用最大厚度積疊，積疊線垂直于最大厚度所在曲面。

1.4 流道型線設計

支板會對流道產生阻塞作用，設計流道型線必須考慮支板的影響。設計流道型線要確定沿流向的面積比，合適的面積分布規律能夠保證過渡段內總的流動比較合理，在面積分布的基礎上修改輪轂和機匣的局部型線來改善局部流動。然后根據圖1中選取的幾何參數，將流道幾何型線與高、低壓渦輪相連，在接口處保證型線在幾何和曲率上的連續，至此完成過渡段的初步設計。

1.5 3維流動校核

利用數值模擬手段對過渡段進行氣動性能校核。氣動性能的要求包括過渡段的流動損失要求和低壓渦輪進口流場的品質要求。若不滿足二者之一則需要考慮是葉型問題還是流道型線問題。確定問題后重新進行1.5步驟，修改完成后進行驗證，直到滿足設計要求為止；如經過若干輪迭代都不能滿足要求，則返回步驟1重新選擇總體幾何參數。

2 過渡段設計

2.1 過渡段原型設計

本次過渡段的總體損失是總壓恢復系數>0.99，設計方案的自由度很低。總參數與流動分離的關系如圖3所示。本方案的總體參數已經靠近分離區域，存在較大的設計難度。

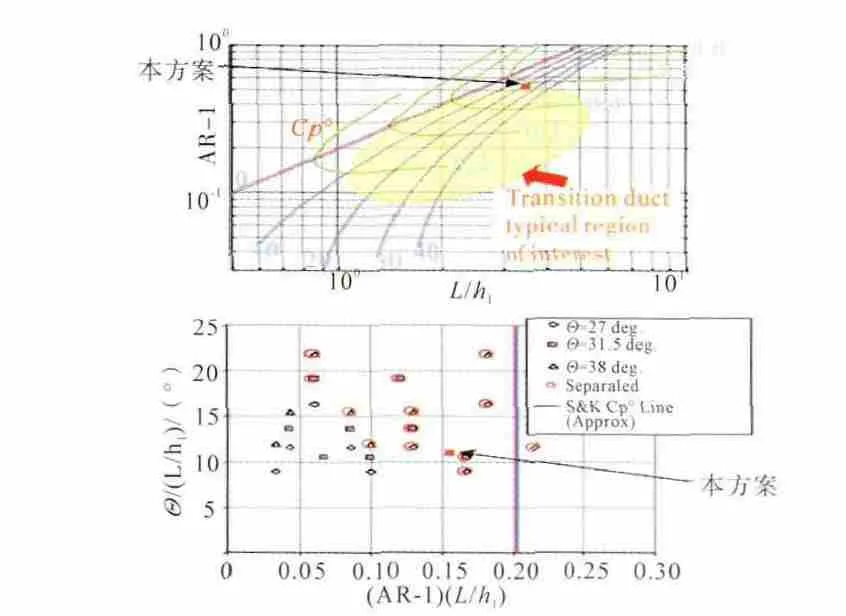
圖3 總體參數與流動分離的關系

過渡段進口平均氣流角與支板幾何構造角相差很小。過渡段進口氣流角如圖4所示。從圖中可見，該邊界條件的氣流角沿徑向分布相當不平衡，從葉根到葉尖氣流角相差近45°。支板稠度很小，整流能力有限。在10%、100%葉高處氣流角與幾何構造角的差值最大，考慮到在過渡段內存在較強的逆壓梯度，在大攻角下很容易在達到支板最大厚度之后引起分離，增加過渡段的損失。所以在設計過渡段時要充分考慮氣流角沿徑向不同分布帶來的問題。

過渡段進口總壓沿徑向分布如圖5所示。從圖中可見，過渡段進口輪轂處的總壓低于平均總壓，說明輪轂處流體機械能小，抵抗逆壓梯度的能力較弱，所以在設計過渡段型線時要通過調整輪轂型線的曲率來提高上端壁處低能流體流通性。機匣處總壓大于進口平均總壓，其流體能量大流通性能比機匣處的好。

過渡段支板的葉型如圖6所示。在設計條件下過渡段進口馬赫數為0.42，所以選擇葉型為低馬赫數下性能優異的葉型作為基準葉型。過渡段的流道如圖7所示。對支板前尾緣均采取一定的掠型處理以減輕對渦輪級的勢干擾。過渡段流道型線的設計遵循面積分布最優原則，在過渡段支板前半部分迅速增加面積，這樣處理雖然使過渡段進口附面層厚度迅速增加，但由于過渡段進口速度較高，可以承受比較大的逆壓梯度。在過渡段后半部分緩慢增加面積，盡可能保持附面層不再增厚。對過渡段流道型線再進行局部修飾，機匣在支板3/4之前上凸，之后稍微回收以加速該部分流體用來改善機匣部分低能流體堆積的情況。通過上面4個步驟的分析，得到初步的過渡段設計方案。

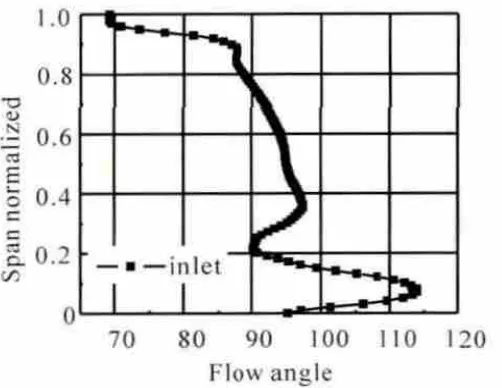
圖4 過渡段進口氣流角

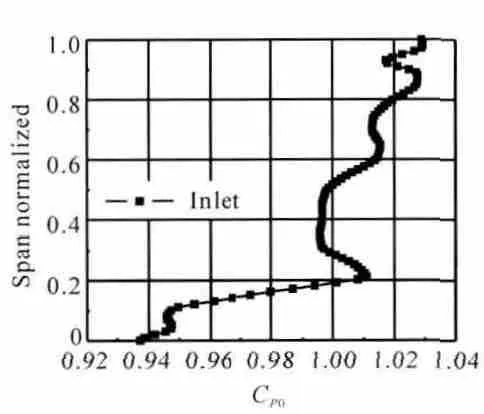
圖5 過渡段進口總壓沿徑向分布

圖6 過渡段支板葉型

圖7 過渡段流道

2.2 過渡段3維數值校核

采用CFX12.0完成數值計算，計算形式為定常單通道。采用時間追趕的有限體積法確定數值，空間離散和時間離散均采用高精度格式（HighResolution），采用多重網格技術加速收斂。工質通過變比熱氣體模擬實際燃氣。湍流模型選取為2方程的SST模型，計算中進口給定總溫、總壓和氣流角，出口給定靜壓平均值。網格采用結構化網格，總數約52萬，所有壁面y+<2，并保證所有壁面附近膨脹比<1.2，符合SST湍流模型對過渡段網格的要求。

2.3 數值模擬結果分析

過渡段數值模擬的總參數結果見表1。從表2可知：總壓恢復系數滿足設計要求，過渡段內的流動損失較小。靜壓升系數較小，表明過渡段的擴壓能力不足。過渡段的出口氣流角接近軸向，說明過渡段的整流能力相對較強。

過渡段不同葉高靜壓升系數與流線如圖8所示。從圖中可見，50%和95%葉高截面的流動和靜壓升系數分布基本合理，流線均勻。支板10%葉高截面處的流動較差，在葉片最大厚度附近存在分離，整個截面的二次流較強，由該處氣流攻角過大引起。從10%和95%葉高截面的靜壓升系數分布可見，在支板前（從輪轂到機匣）存在較強的徑向壓力梯度，導致較強的徑向遷移，增加二次流損失。

過渡段內部流動分離如圖9所示。從圖中可見，分離發生于支板前緣和輪轂支板厚度最大處附近。支板前緣分離主要由來流的攻角較大引起，而且機匣處支板前緣的分離區小于輪轂處支板前緣的分離區，這是由2個原因引起：從進口邊界條件分析可知機匣處的攻角小于輪轂處的攻角；機匣處的流體經過吸力峰的加速后抵抗分離的能力較強。輪轂處分離的形成原因是來流處輪轂的流體總壓較低（僅為平均值的94%），說明該處流體速度較低，且在輪轂處是減速增壓，所以該處流體抵抗分離的能力較弱。

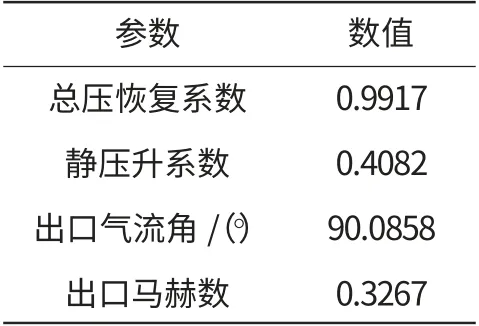
表1 過渡段數值模擬結果

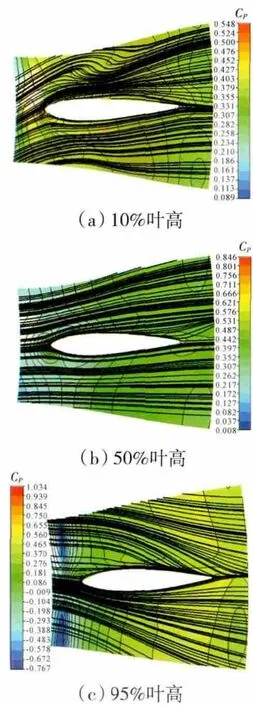
圖8 不同葉高截面葉高靜壓升系數與流線

從支板表面極限流線可知，機匣上端壁附近存在較強的二次流，主要由于過渡段支板展弦比極小，且徑向壓力梯度較大所致。同時支板靠近0°一側的流動狀態明顯差于靠近30°一側的。這是由輪轂處很大攻角導致的，它讓支板表面的徑向遷移更加嚴重。

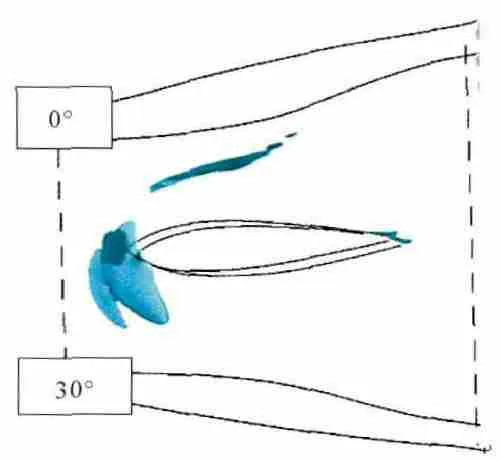
圖9 過渡段內部流動分離（速度<0的等值面）

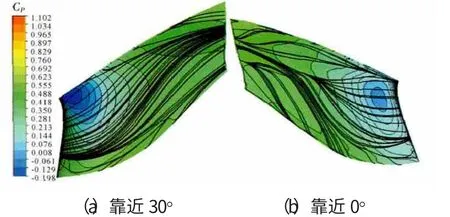
圖10 支板表面靜壓與極限流線

過渡段輪轂和機匣周向平均靜壓升系數分布如圖11所示。從圖中可見過渡段輪轂和機匣的流動特點。沿著機匣端壁，首先會有一小段的順壓力梯度，在第1個彎角處出現吸力峰，隨后流道面積迅速擴大，與型線曲率共同導致流道內存在很強的逆壓梯度，靜壓升系數迅速增大，這段強逆壓梯度作用區大致結束于支板最大厚度附近，之后直至過渡段出口，流體處于1個弱逆壓梯度作用下，在輪轂處，氣流1彎之前流體受到1個弱逆壓梯度，之后的流體處于1個更微弱的逆壓梯度作用之下直至80%軸向位置處，從80%軸向位置到出口流體處于順壓力梯度作用下，這主要是機匣型線上凸后，局部修型與低壓渦輪流道光滑連接所致。

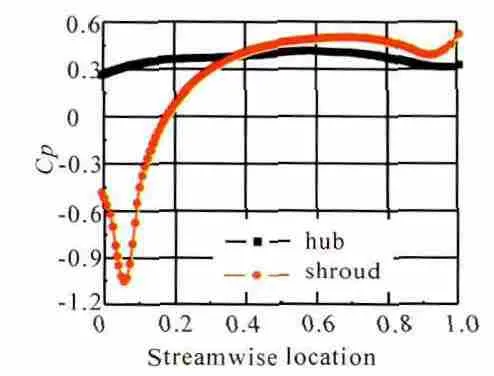
圖11 過渡段機匣周向平均靜壓升系數沿軸向分布

上述分析說明：輪轂處的流體所處的逆壓梯度較弱，流動狀態較好，因此在輪轂處理論上不應該出現分離。但是輪轂的流動明顯比機匣的差，且產生了流動分離，這是由進口邊界條件所引起。輪轂處的流體存在較大攻角，且流體總壓較低，為低能流體，抵抗分離的能力很弱，容易在靠近0°一側形成分離。

圖12過渡段出口軸向馬赫數分布如圖12所示。從圖中可見，過渡出口軸向馬赫數在周向分布不均，在機匣處高而在輪轂處低，這主要由來流邊界條件所導致。在支板尾跡區域存在1個低軸向馬赫數區域，該區域的形成與靠近0°一側支板葉中形成的強二次流有關。按照文獻[10]所述，強二次流會產生較大損失。

分析出口截面的軸向馬赫數可知，過渡段的出口不能為下游的低壓渦輪提供高品質的來流。

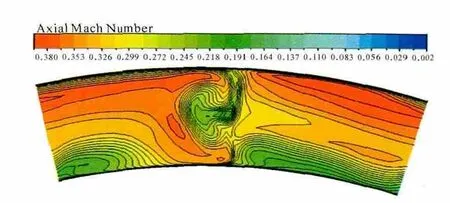
圖12 過渡段出口軸向馬赫數分布

過渡段進、出口周向平均的總壓系數沿徑向的分布如圖13所示。從圖13中可見，在經過過渡段之后，輪轂處的總壓系數與平均值間的差值變小，說明輪轂流體在通過過渡段時與高能流體發生能量交換，且從圖11可見，在40%軸向位置之后存在從機匣到輪轂的壓力梯度，這種壓力梯度會引起從機匣到輪轂的徑向遷移，使輪轂區域的流體能量得到恢復，有利于提高流場的均勻性。

過渡段進、出口周向平均總壓系數和氣流角沿徑向的分布如圖14所示。從圖中可見，經過過渡段之后，氣流角的不均勻性明顯改善。10%葉高流體的攻角基本消除，在80%葉高以下的流體氣流角都接近軸向的，只有機匣區域的的氣流角與軸向還相差10°。這是由于機匣區域一直處于逆壓梯度作用下，附面層比較厚所引起的。

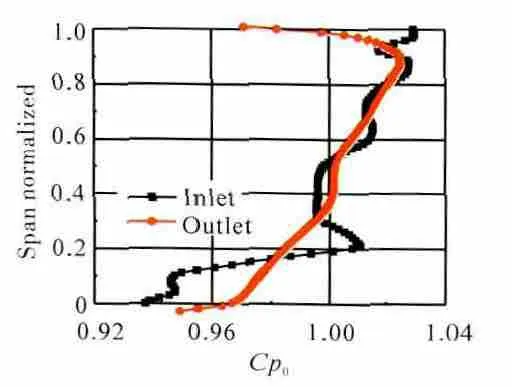
圖13 過渡段出口周向平均總壓系數沿徑向分布[13-14]

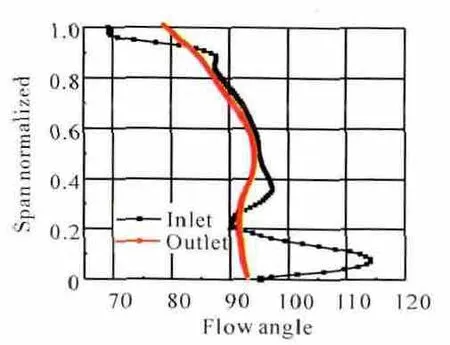
圖14 過渡段出口周向平均氣流角沿徑向分布

過渡段內損失主要由摩擦損失、附面層分離損失和二次流損失組成[15]。過渡段進口馬赫數較低，所以摩擦損失不大；二次流損失與過渡段的來流條件和具體流動有關，在本算例中由于來流條件很不均勻，摻混損失較大，因此產生的二次流損失較大；本算例中在輪轂處出現分離，所以會有一定的分離損失。

通過對原型過渡段的數值模擬可以發現本算例存在2個問題：支板表面存在很強的二次流，且過渡段出口的流場均勻度不符合低壓渦輪進口條件要求；在輪轂處存在流動分離，影響周圍流體的流動狀態。因此需對此進行改進。

2.4 過渡段氣動設計改型

依據過渡段設計流程圖進行改型設計。在改型設計中考慮到葉根進口總壓過低，輪轂的擴壓不宜過大，通過調整輪轂流道型線對機匣和輪轂的壓力分布重新設計，改善過渡段流道內的二次流，消除輪轂區域的分離團。原型過渡段支板的性能較好，所以在改型過渡段中未修改。

原型與改型過渡段流道對比如圖15所示。從圖中可見，考慮到葉根進口總壓過低，輪轂的擴壓不宜過大，改型修正通過調整輪轂流道型線的方式對機匣和輪轂的壓力分布重新設計。原型設計中機匣處的流動較好，所以在改型設計中未修改。過渡段原型與優化方案面積比沿流向分布如圖16所示。從圖中可見，優化設計主要是修正原型產生分離區域的流向面積分布規律。

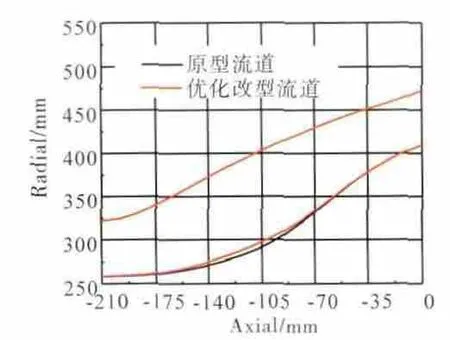
圖15 原型與改型過渡段流道對比

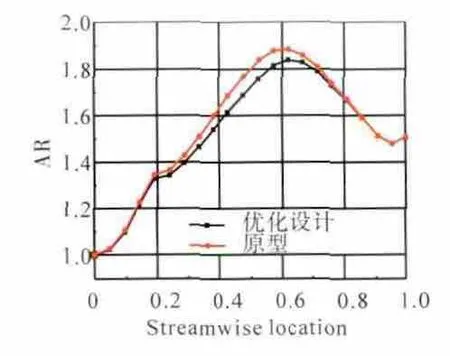
圖16 過渡段原型與優化方案面積比沿流向分布

對優化設計過渡段進行CFD3維數值模擬，并將其與原型過渡段的總參數對比分析，結果見表2。從表2可知，過渡段出口的總壓恢復系數明顯增大。過渡段出口的靜壓升系數增大，說明過渡段出口的擴壓能力提高，流動得到改善。過渡段之后馬赫數降低，對低壓渦輪的設計有利。

過渡段內部流動分離如圖17所示。從圖中可見，在過渡段輪轂處的分離已經消除，但是過渡段支板前緣的分離尚在，這是因為支板前緣的分離團由來流條件決定，除非改變支板的幾何構造角，否則分離無法消除。而優化的過渡段已經消除了流動分離，證明優化效果比較明顯。

過渡段出口周向平均總壓系數沿徑向分布如圖18所示。從圖中可見，優化改型對總壓系數沿徑向的分布影響不大，但由于減小了二次流，所以在40%區域強二次流產生的總壓虧損有所改善。

過渡機匣出口的軸向馬赫數如圖19所示。相對于原型，過渡段出口的流場有一定改善，但優化的過渡段出口軸向馬赫數在周向分布還很不均勻，在機匣處高，主要是來流邊界條件所造成的。在支板40%葉高尾跡附近存在1個低軸向馬赫數域，其形成與靠近0°一側支板葉中形成的強二次流有關。由于過渡段支板是對稱葉型，過渡段一側的流動好而另一側的不好，這是由來流邊界條件形成的，只修改支板和流道型線對改善支板上的強二次流作用不大。

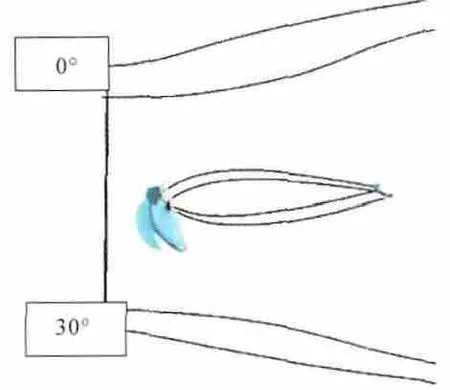
圖17 過渡段內部流動分離（速度小于0的等值面）

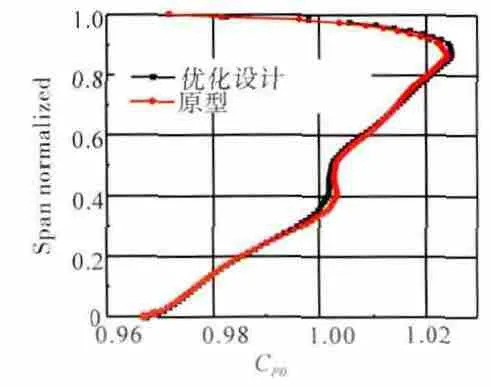
圖18 過渡段出口周向平均總壓系數沿徑向分布

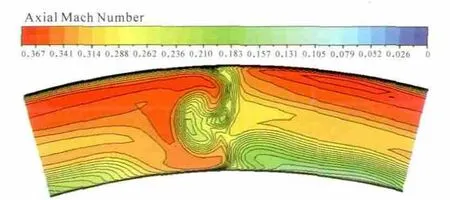
圖19 過渡段出口軸向馬赫數分布

3 結論

本文依據過渡段設計流程的5個步驟對某大涵道比發動機的過渡段進行氣動設計，并在原設計的基礎上進行了改型設計，得到以下結論：

（1）本文提出的過渡段5步設計流程方法可行，有較高的實用價值。

（2）通過控制流向面積分布規律能夠確定過渡段沿流向的壓力分布，改變過渡段流道型線的曲率能夠改善改形區域附近的局部流動。

（3）在過渡段的設計中要重視并充分考慮對來流邊界條件的分析，必要時對將高壓渦輪和過渡段作協同設計，以保證低壓渦輪的進口流場品質。

[1]鄒正平，周琨，王鵬，等.大涵道比渦扇發動機渦輪內部流動機理及氣動設計技術研究發展[J].航空制造技術，2012，13（1）：49-54.ZOU Zhengping，ZHOU Kun，WANG Peng，et al.Research progress on flow mechanism and aerodynamic design method of high-bypass-ratio engine turbine[J].Aeronautical Manufacturing Technology，2012，13（1）：49-54.（in Chinese）

[2]Dominy R G，Kirkham D A.The influence of swirl on the performance of inter-turbine diffusers[J].VDI Berichte，1995，116（1）：107-122.

[3]Dominy R G，Kirkham D A.The influence of blade wakes on the performance of inter-turbine diffusers[J].ASME J.Turbomach，1996，118（2）：347-352.

[4]Norris G，Dominy R G，Smith A D.Flow instability within a diffusing,annular S-shaped duct[R].ASME 1998-GT-425.

[5]蔣首民.渦輪過渡段流動機理及設計技術研究[D].北京：北京航空航天大學，2014.JIANG Shoumin.Research on flow mechanism and design technique of intermediate turbine duct[D].Beijing：Beihang University，2014.（in Chinese）

[6]谷曉剛.高功重比渦軸發動機渦輪過渡段復雜流動研究[D].北京：北京航空航天大學,2014.GU Xiaogang.Research on complex flow field of high power-weight ratio turbine shaft engine[D].Beijing：Beihang University，2014.（in Chinese）

[7]毛凱，吳虎，徐倩楠.大涵道比渦扇發動機渦輪過渡段的數值研究[J].科學技術與工程，2012，20（6）：1308-1313.MAO Kai，WU Hu，XU Qiannan.Numerical research for intermediate turbine duct of high bypass turbofan engine[J].Science Technology and Engineering，2012，20（6）：1308-1313.（in Chinese）

[8]Marn.On the aerodynamics aggressive intermediate turbine ducts competitive and environmentally friendly jet engines[D].Melbourne：Graz University of Technology，2008.

[9]Zhang X F，Hu SZ，Benner M，et al.Experimental and numerical study on an inter-turbine duct[R].ASME 2010-GT-37322.

[10]Wallin F，Eriksson L E，Nilsson M.Intermediate turbine duct design and optimization[C]//25th Congress of the International Council of the Aeronautical Sciences (ICAS).St Petersburg,Russia,2006,5（1）：1-10.

[11]孫志剛，黃洪雁，譚春青，等.某型燃機渦輪過渡段流場優化設計[J].工程熱物理學報，2008，29（6）：940-942.SUN Zhigang，HUANG Hongyan，TAN Chunqing，et al.Optimization design for the turbine transition section of an aeroengine[J].Journal of Engineering Thermophysics，2008，29（6）：940-942.（in Chinese）

[12]Couey P T，Keever M，Malak C W，et al.Computational study of geometric parameter influence on aggressive inter-turbine duct performance[R].ASME 2010-GT-23604.

[13]Sovran G，Klomp E D.Experimentally determined optimum geometries for rectilinear diffusers with rectangular,conical or annular cross-section [J].Fluid Mechanics of Internal Flow，1967，20（21）：413-427.

[14]Denton J D.Loss mechanisms in turbomachines[J].Journal of Turbomachinery，1993，115（4）：621-656.