尋找單位“1”之淺見

靖潔

（河北省定州市周村鎮北車寄小學）

尋找單位“1”之淺見

靖潔

（河北省定州市周村鎮北車寄小學）

我國2011年農村居民人均純收入為6977元，比上年增長17.9%，我國2010年農村居民人均純收入是多少元？（冀教版六年級上冊教材第60頁例題）

老師：看到此題，你有何想法？

學生A：我覺得從“比上年增長17.9%”中的“比”字就可以知道，這個題是把“上年”，也就是“我國2010年農村居民人均純收入”看作是單位“1”，而問題又正好是求我國2010年農村居民人均純收入的，所以，這是一道求單位“1”是多少的問題。

學生B：我覺得從“增長17.9%”，即增長上年的17.9%可以知道，這就是把“我國2010年農村居民人均純收入”看作單位“1”的百分數應用題，所以我同意他的看法，且是求單位“1”是多少的百分數應用題。

老師：太棒了，那又如何解決問題呢？

學生C：此題有一等量關系式，這個等量關系式是：我國2010年農村居民人均純收入+比上年（2010年）增長的17.9%=我國2011年農村居民人均純收入，所以我們可以運用方程法來解決。

解：設我國2010年農村居民人均純收入是x元

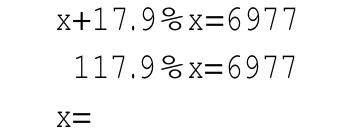
答：我國2010年農村居民人均純收入是（）元。

學生D：這道題中，把“我國2010年農村居民人均純收入”看作是單位“1”。而我國2011年農村居民人均純收入6977元占我國2010年農村居民人均純收入的（1+17.9%），求我國2010年農村居民人均純收入是多少，即求單位“1”，可以用除法計算。

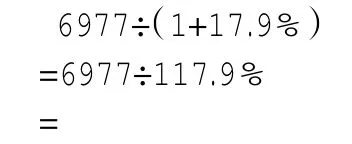
答：2010年我國農村居民人均純收入是（）元。

以上是一道關于百分數應用題的教學。在小學數學教學中，分數百分數應用題是教學的一個重要內容，也是小學數學教學的一個難點。而解決此類問題的關鍵是找準單位“1”，而這又是困擾小學生的一個關口，因為題目中的單位“1”有時明顯，有時含蓄。怎樣幫助學生快速找到單位“1”，順利從橋這頭到達橋那頭，我們可以試著從以下幾個方面入手。

首先，我們可以從分數的意義來向學生說明什么是單位“1”，而所謂的“分數”就是指把單位“1”平均分成若干份，表示這樣的一份或幾份的數。所以由分數的意義我們就可以知道，要把誰平均分，誰就是單位“1”。但是我們要知道這個單位“1”不僅僅可以代表自然數1，它還可以是一個物體、一個圖形、一個計量單位，而且由許多物體組成的一個個整體也可以是單位“1”，如，一摞書、一盒粉筆、一袋蘋果、一個生產任務、一項工程等。

綜上所述，這是一道把全書頁數看作單位“1”且求單位“1”的分數應用題。

其次，可以尋找一些標識性的詞語，像是、占、比等，這些字會告訴我們單位“1”是誰。只因單位“1”就是個參照物，用誰參照就設誰是為單位“1”。

又比如：在一次期中考試中，全班共有32名同學，其中及格的人數占全班人數的95.2%，比優秀人數多14.5%，問優秀人數有多少？

分析：及格人數占全班人數的95.2%，就是把全班人數看作單位“1”，比優秀人數多14.5%，是指及格人數比優秀人數多優秀人數的14.5%，所以這句話是把優秀人數作參照物，所以優秀人數是單位“1”。所以要求優秀人數得先求及格人數后再求。

第三，在一些題目中，沒有標識性的詞語，單位“1”不容易被人發現，這時我們可以采用填空的方法找到并確認單位“1”。

例如：一件衣服，原價800元，商場降價出售，現價720元，問降價百分之幾？

分析：考慮“降價百分之幾？”，首先考慮降誰的價，由題目可知，降的是原價的價，所以填空“降（原價的）百分之幾”，即降價部分占原價的百分之幾。由此得出此題目把原價看作單位“1”。

再如：某廠5月份生產70噸貨，6月份產量達到77.5噸，問增產百分之幾？

分析：同理，我們首先考慮的是增誰的產，本題中，6月份產量比5月份多，5月份的產量發生變化，增產了，求增產百分之幾，就是（求6月份比5月份）增產（的部分占5月份的）百分之幾，填完空，找到5月份的產量為單位“1”。

第四，在某些表示整體的分數應用題中，如果部分量和總量作為比較關系出現，并且部分量是作為比較量，而總量是作為標準量，那么總量就是單位“1”。

由此可見，在解答這一類的分數應用題時，關鍵是要找對總量和部分量，確定出單位“1”就很容易了。

當然，只是找到題目中的單位“1”還沒完全解決問題，還需要弄清楚題目是求單位“1”的，還是求單位“1”的多少的，只有這樣才能最終確認做題方法。而尋找單位“1”也不僅僅這些方法，同時這些方法也不是獨立的，同一題目中，這些方法可以交錯使用。小學數學雖面廣，但無論哪種題型，只要我們抓住其根本，吃透內涵，總會獲得成功！

·編輯 魯翠紅