液艙三維晃蕩運動二階共振理論解及特性分析

楊小巖，張洪生，吳鵬飛，2

(1.上海海事大學 海洋科學與工程學院，上海 201306;2.上海交通大學海科集團有限公司，上海200231)

隨著LNG 船這類載液貨物船型的普遍應用，晃蕩問題逐漸成為海洋工程水動力學的研究熱點［1-3］。由晃蕩而產生的共振問題也顯得尤其重要。共振是自然界非常重要的現象，當外部激發頻率等于系統的某一固有頻率時就會發生共振現象。文獻［4］采用線性理論分析了液艙內二維液體的晃蕩問題。當外部激發頻率等于固有頻率時，液艙內液體晃蕩發生共振。文獻［5-12］采用不同的數值方法，如有限元法和非線性模態法等，研究了液艙內液體的非線性共振問題。盡管根據非線性理論可以得出結論，當共振發生時自由液面的高程不可能趨于無窮大，但仍然具有較大的振幅。這仍可能導致對液艙的猛烈沖擊，從而使其發生破壞。

文獻［13］研究發現，除了一階共振在液艙晃蕩中的影響比較重要外，二階共振也很重要。隨后，文獻［14］通過完全非線性理論，文獻［15-16］通過PSME(Pseudo Spectral Matrix-Elements 偽譜矩陣元)法，文獻［17-18］通過時域分析方法分別證實了二階共振的重要性。前人對二階共振的研究多采用模型試驗和數值計算方法，而對二階共振的理論研究只局限于某一方向上的振蕩，如縱蕩或橫蕩運動。實際上，對于大多數晃蕩問題，液艙運動包括所有運動模式［19］。例如，船舶運動通常結合了縱蕩和橫蕩運動。線性理論只能考慮簡單的縱蕩和橫蕩運動的疊加，而不能考慮它們之間的耦合。然而，對于二階問題，不再是簡單的疊加運動，而需要考慮兩個方向的耦合運動。這種由兩個方向的耦合運動所產生的耦合項在文獻［13］所考慮的單一方向運動、二維二階共振的問題中是不存在的。文中考慮了三維二階共振問題中的耦合運動，還研究了各個二階共振激發頻率下水深變化對晃蕩振幅的影響。

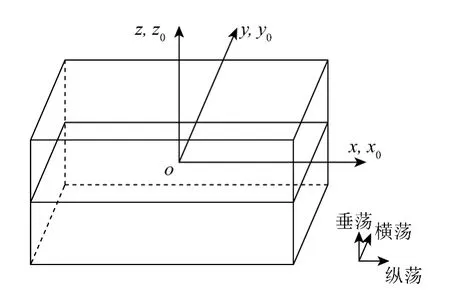
圖1 笛卡爾坐標系ox0y0z0 和oxyzFig.1 Cartesian coordinate systems ox0y0z0 and oxyz

1 二階共振的理論解

1.1 基本方程和邊界條件

考慮一個三維長方體液艙模型，長為2l，寬為2b，液艙內水深為d，并同時作橫蕩和縱蕩的三維晃蕩運動。假定液艙中液體為無黏、不可壓和運動無旋。在液艙上建立一個右手笛卡爾坐標系ox0y0z0，原點位于初始靜止狀態自由液面的中央，z0方向垂直向上，如圖1 所示。假定液艙在x0方向和y0方向的位移分別是s1(t)和s2(t)。

液艙中液體運動的速度勢φ 滿足三維拉普拉斯方程:

自由液面高程可以用z0= η (x0，y0，t)表示，則邊界條件為

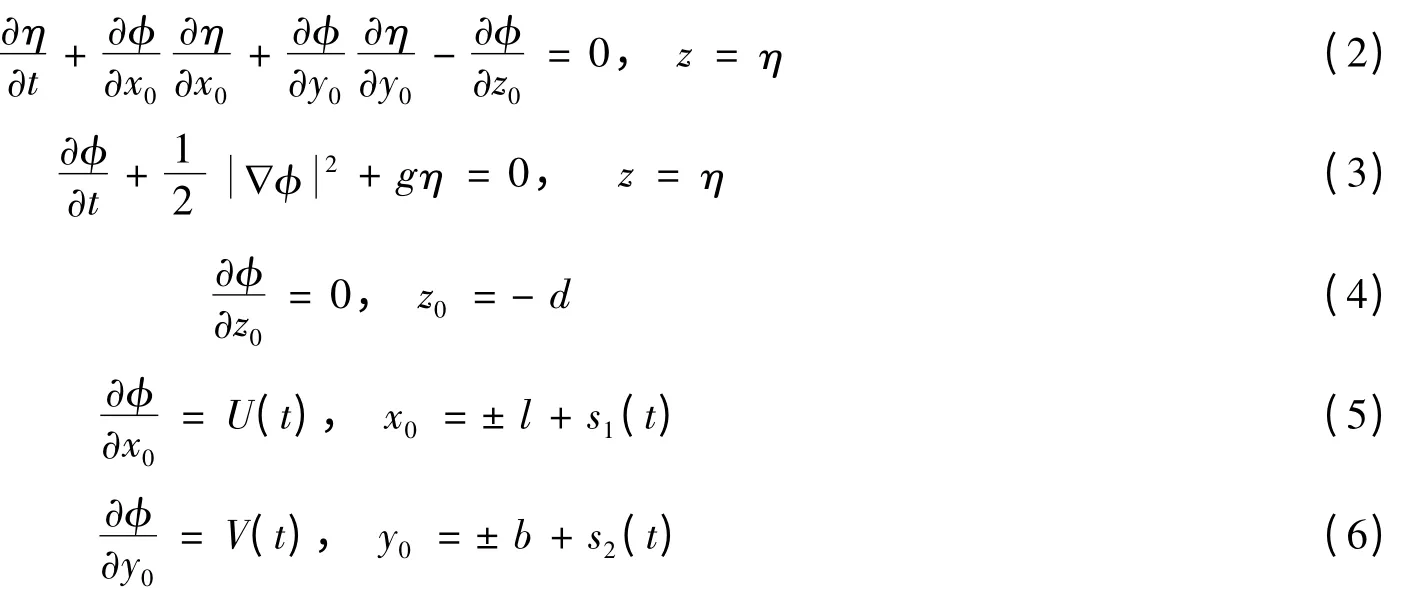
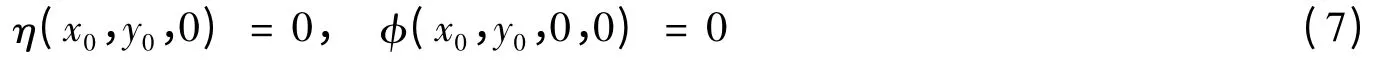
在液艙運動系統中建立另外一個笛卡爾坐標系oxyz，如圖1 所示。它與坐標系ox0y0z0的關系可以表示為

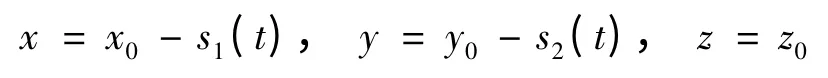
因而在坐標系oxyz 下，式(2)～(6)可分別表示為

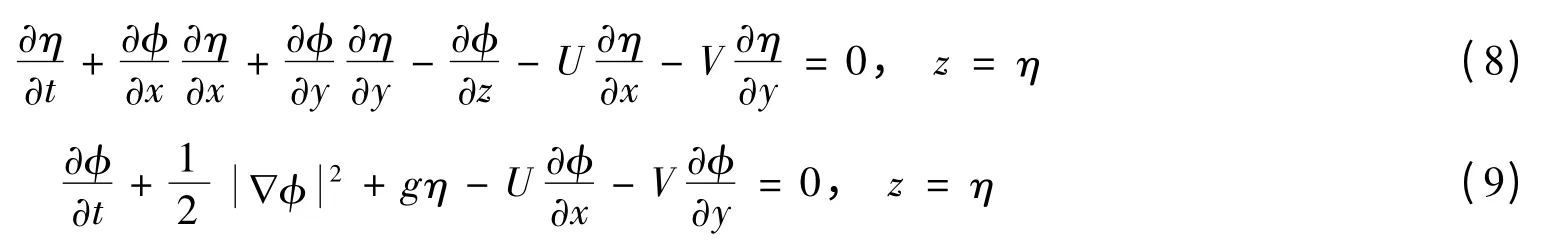
根據微擾理論，在z = 0 (靜水面)處展開，由式(8)和(9)分別可得

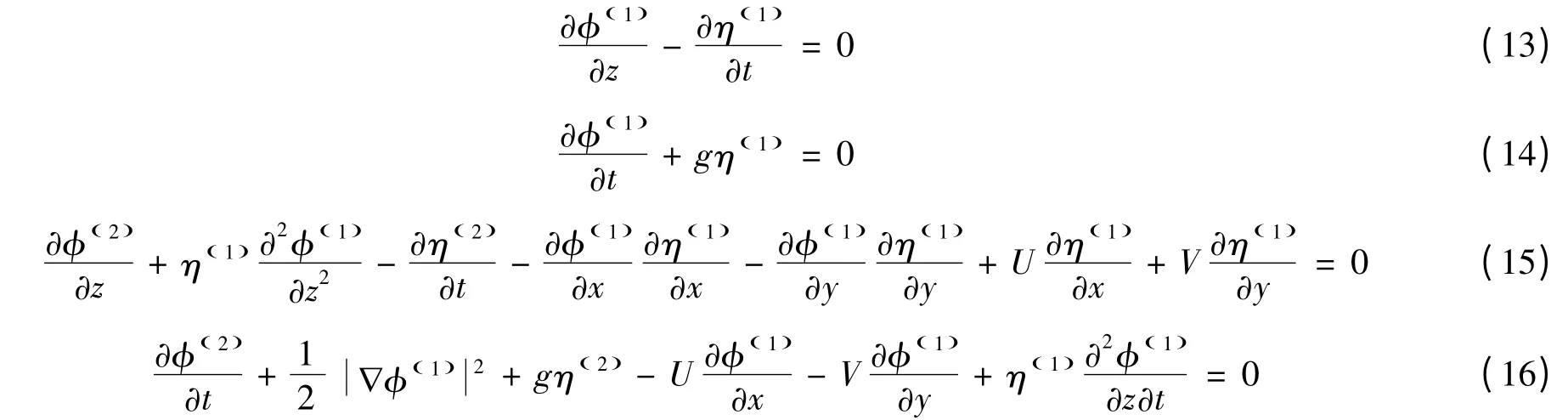
類似地，根據微擾理論，由式(10)～(12)分別可得

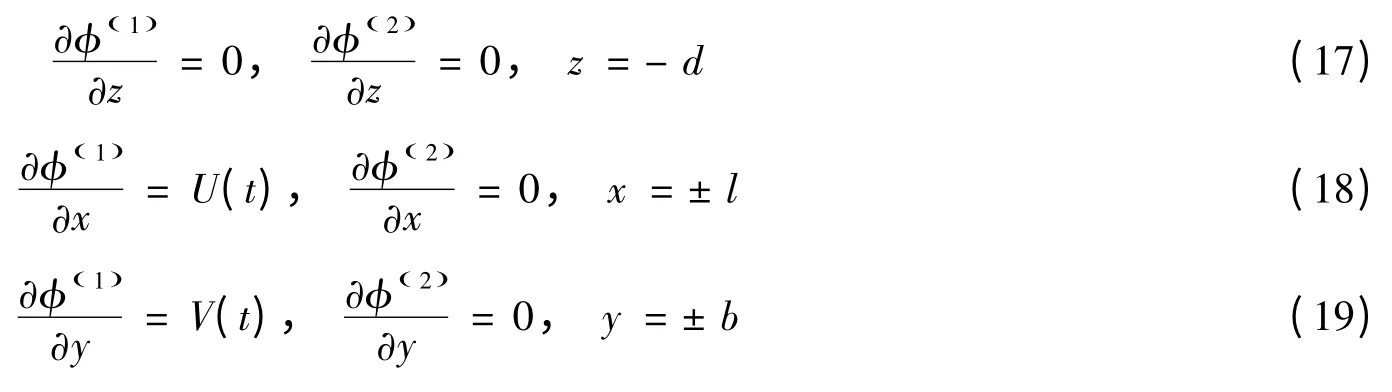
1.2 一階共振的理論解

由于一階速度勢φ(1)和一階波面函數η(1)是線性的，它們可分別通過直接將橫蕩和縱蕩的一階解進行線性疊加而得到。假定和分別為橫蕩和縱蕩的速度勢一階解，和分別為橫蕩和縱蕩的波面函數一階解，三維晃蕩問題一階速度勢φ(1)和一階波面函數η(1)的表達式分別可寫為

由文獻［13］可得

式中:Am，Bm，Jp和Kp為未知系數;km= mπ/2l，jp= pπ/2b。

1.3 二階共振的理論解

對式(16)求關于t 的導數，并代入式(15)，可得

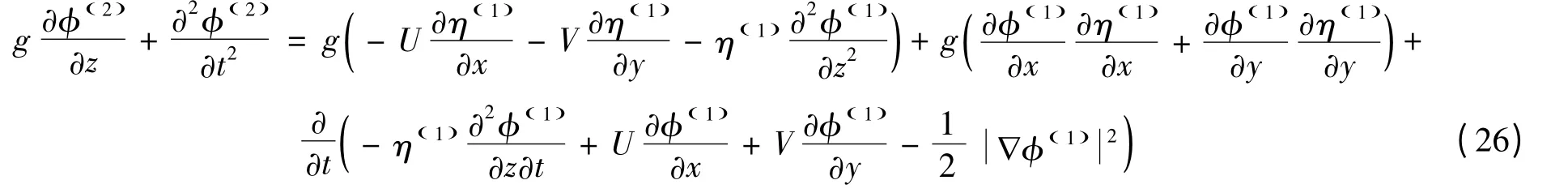
將式(20)和(21)分別代入式(26)，簡化處理后可得

在式(27)中，等號右邊可以分為三個部分

假設

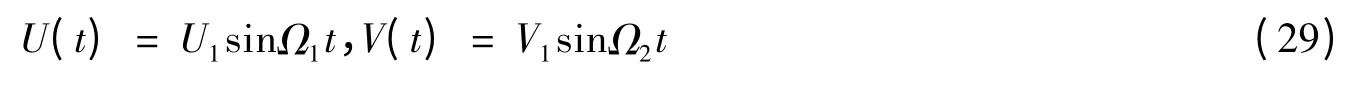
由文獻［13］可知

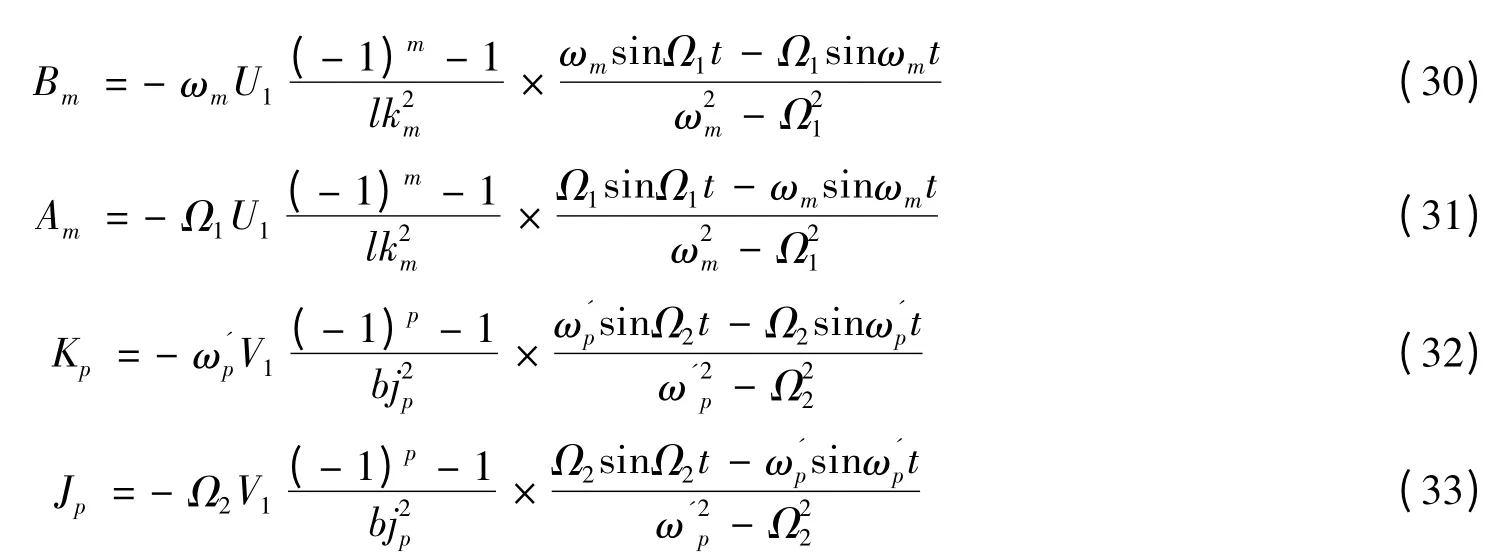
將式(22)～(25)和式(30)～(33)代入式(27)的最后一部分，整理后得到

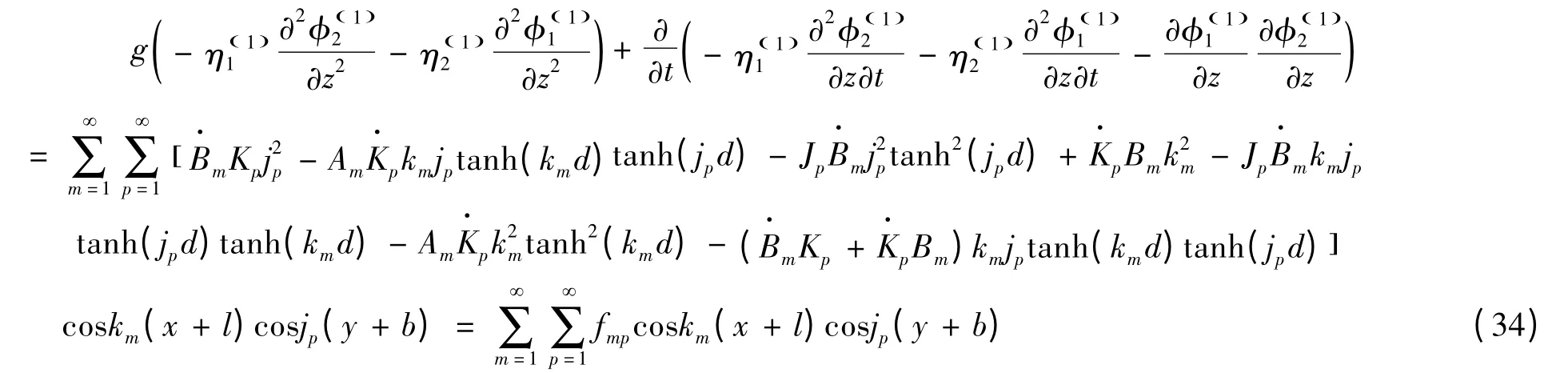
其中，

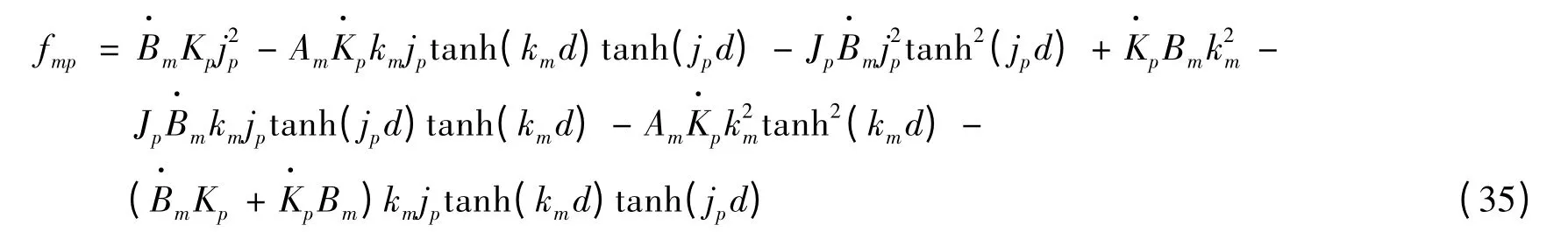
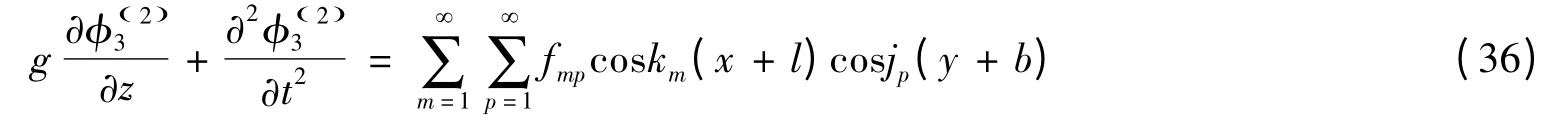
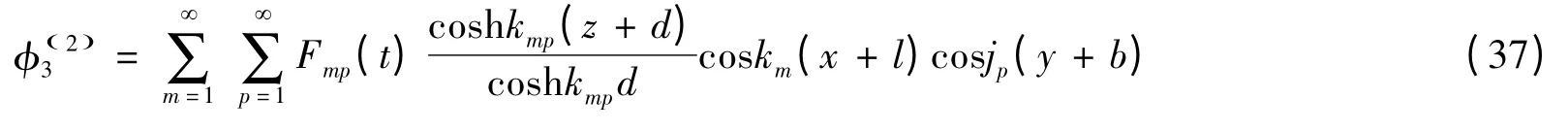
將式(37)代入式(36)，整理可得

Fmp(t)的初始條件可從式(7)得到，再由式(16)，可得

利用拉普拉斯變換和逆變換，可得式(38)的解，即

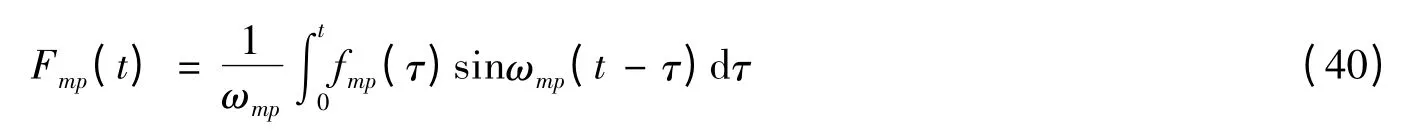
式(40)表明當fmp(τ)包含周期項ωmp，并當t →∞時，Fmp(t)趨近于無窮大。

2 二階共振的特性分析

2.1 二階共振發生的條件

在液艙以U(t)= U1sinΩ1t、V(t)= V1sinΩ2t 的速度做三維晃蕩運動的情況下，從式(34)可以發現，Ω2都為速度勢二階解中耦合項的周期項，ωm和ω'

p 分別為x 和y 方向的固有頻率，從文獻［5］可知，三維晃蕩液艙的固有頻率為ωmp(m，p = 1，3，…)。

顯然，當m，p = 2，4，…時根據式(35)有fmp= 0 ，意味著偶模只對應于橫蕩或者縱蕩的單一方向的晃蕩，而奇模則對應于橫蕩與縱蕩同時發生時產生的耦合項。當橫蕩固有頻率為奇模，縱蕩固有頻率為偶模即ωmp(m = 1，3，…;p = 2，4，…)或對應橫蕩固有頻率為偶模，縱蕩固有頻率為奇模即ωmp(m = 2，4，…;p = 1，3，…)時，有fmp= 0 ，因而二階共振也不會發生。而如果3，…中任意一個頻率等于液艙某個滿足奇模的固有頻率ωmp(m，p = 1，3，…)時二階共振則會發生。

對奇模進行分析，設m = p = 1 。根據式(40)可知F11反映了所討論的二階共振發生時波高的變化。假定液艙尺寸長寬大小為l = d、b = 0.4l。圖2(a)和2(b)分別給出了當Ω2+Ω1= ω11和Ω2－ Ω1= ω11時，無量綱波高，即的變化情況。由圖2 可知，對應于奇模的這兩種情況，發生了明顯的共振。

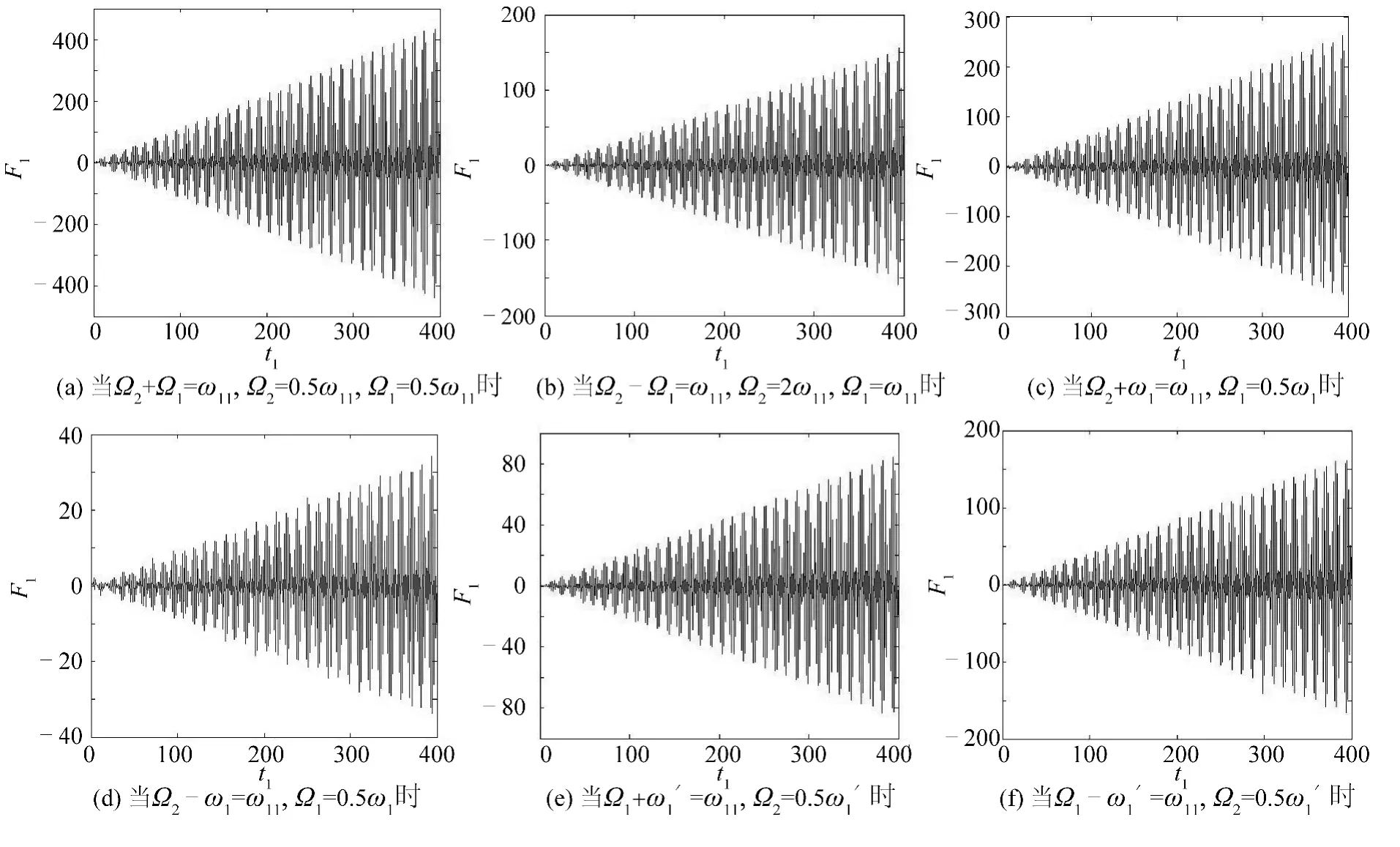
圖2 不同條件下F1 相對于t1 的變化Fig.2 F1 against t1 under different conditions

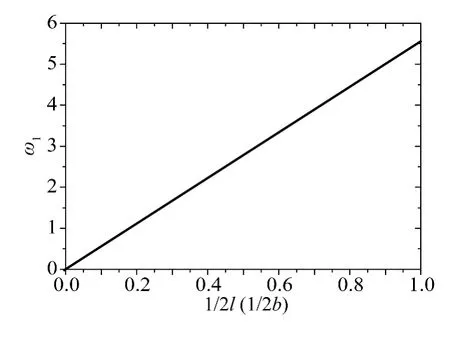
圖3 相對于1/2l(或者1/2b)ω1 的變化Fig.3 ω1 against 1/2l(or 1/2b)

再來考慮二階共振的另外一個例子，圖2(c)和2(d)分別給出了當Ω2±ω1= ω11，Ω1= 0.5ω1時波高隨時間的變化情況。結果同樣表明隨著時間的增加波高逐漸變大。由圖2(e)和2(f)可知，當Ω1±= ω11，Ω2，也有類似現象。以上的例子表明，當某一方向外部激發頻率與某一固有頻率和其另一方向晃蕩的固有頻率的和相等時，二階共振也會產生。

由式(34)可以發現，當ω'p + ωm滿足下式時，二階共振可能發生。

然而，式(41)只有當d/2l 和d/2b 取某些特定值時才成立。假設d = 1 、m = 1 ，圖3 給出了ω1相對于1/2l(或者1/2b)的變化情況。從圖3 可知，只有當1/2l?0.1 或1/2b ?0.1 時式(41)才成立，也就是說d/2l 或d/2b 是非常小的量，這也就意味著水深是非常淺的。然而，在水深很淺的條件下任何可能的二階共振都沒有實際的意義。

2.2 液面高度對二階共振振幅的影響

眾所周知，液艙尺寸大小比例、初始運動狀態、激發頻率和液艙內液深是影響晃蕩幅值的幾個重要因素。文獻［15］在采用PSME 方法對于二維晃蕩二階共振的研究中，對這上述幾個影響晃蕩共振的因素進行了詳細的討論和對比分析。

采用Matlab 軟件，對不同深度液體的晃蕩共振情況進行模擬，并討論液艙內液體不同深度情況下三維晃蕩共振的特性。由于篇幅限制，只給出了在不同液深情況下和頻效應所激發的無量綱波高隨時間變化的曲線。

算例1，Ω2+ Ω1= ω11

圖4 為Ω2+ Ω1= ω11時，d = 0.4l、d = l 和d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的情況。在此激發頻率下，對比圖4(a)～(c)明顯可以看出，當t1= 200 時，液艙中液體晃蕩高度分別為400、200 和180 左右;當t1= 400 時，晃蕩高度分別達到800、400 和350 左右。由此可見，在輸入頻率為兩方向外部激發頻率的和頻時，液體深度對晃蕩作用的影響是明顯的，液體深度越小，其二階共振晃蕩的振幅就越大。

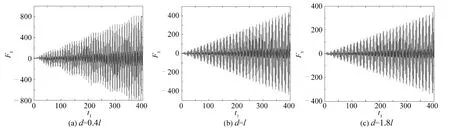
圖4 不同液深情況下F1 相對于t1 的變化Fig.4 F1 against t1 in the case of different water depths in tank as Ω2 + Ω1 = ω11

當Ω2－Ω1= ω11時，根據d = 0.4l、d = l 和d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的曲線可以得到，當t1= 200 時，液艙中液體晃蕩高度分別為50、70 和80 左右;當t1= 400時，晃蕩高度分別達到100、140 和160 左右。由此可見，在輸入頻率為兩方向外部激發頻率的差頻時，液體深度對晃蕩作用的影響不如和頻情況下明顯。

由圖5(a)可以看出，當d/l ≤1.0 時，曲線下降趨勢較陡，說明液深變化對于二階共振晃蕩幅度的影響較大;而當d/l ≥1.0 時，曲線下降趨勢較緩，說明液深變化對于二階共振晃蕩幅度的影響變小。由圖5(b)可以看出，曲線依舊由陡變緩，但振幅數值變化較輸入頻率為兩方向外部激發頻率的和頻時要小;且與和頻情況不同的是，二階共振晃蕩振幅隨著液深的增大而增大。

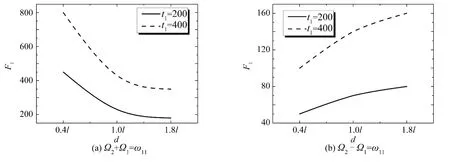
圖5 當t1 一定時不同液深情況下F1 的變化Fig.5 F1 against the water depth in tank at t1 = 200 and t1 = 400 ，respectively

算例2，Ω1+= ω11

圖6 為Ω1+= ω11時，d = 0.4l、d = l、d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的情況。在此激發頻率下，對比圖6(a)～(c)明顯可以看出，當t1= 200 時，液艙中液體晃蕩高度分別為15、35 和40 左右;當t1=400 時，晃蕩高度分別達到30、70 和80 左右。由此可見，在輸入頻率為某一方向外部激發頻率與另一方向的固有頻率的和頻時，液體深度越大，其二階共振晃蕩的振幅就越大。

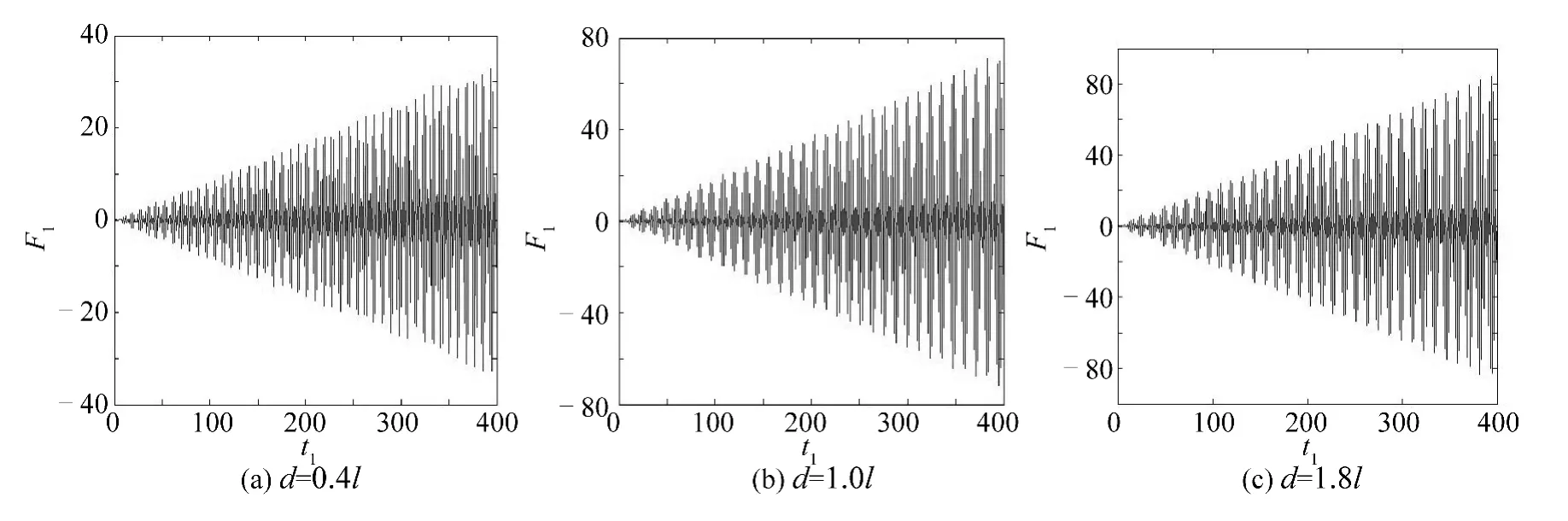
圖6 不同液深情況F1 相對于t1 的變化Fig.6 F1 against t1 in the case of different water depths in tank as Ω1 + ω'1 = ω11

當Ω1－= ω11時，根據d = 0.4l、d = l、d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的曲線可以得到，當t1= 200 時，液艙中液體晃蕩高度都為70 左右;當t1= 400 時，晃蕩高度分別達到130、150 和140 左右。由此可見，相對于輸入和頻，在輸入頻率為某一方向外部激發頻率與另一方向的固有頻率的差頻時，液深的變化對二階共振振幅的影響還是比較小的。

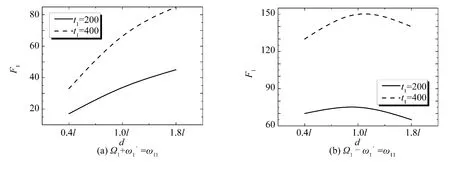
圖7 當t1 一定時不同液深情況下F1 的變化Fig.7 F1 against the water depth in tank at t1 = 200 and t1 = 400 ，respectively

當0 ＜d/l ＜2.0 時，由圖7(a)可以看出無量綱波高值不大，說明此時液艙內液面晃蕩現象并不明顯，但二階共振確實已經發生。由曲線先陡后緩的變化趨勢可以看出，液深變化在d/l ≤1.0 區域時對于二階共振晃蕩幅度的影響相對較大。由圖7(b)可以看出，液深變化對其差頻二階共振晃蕩振幅的影響很小。特別地，當t1= 200 時，其對二階共振晃蕩振幅的影響趨近于零。

算例3，Ω2+ ω1= ω11

圖8 為Ω2+ ω1= ω11時，d = 0.4l、d = l、d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的情況。在此激發頻率下，對比圖8(a)～(c)可以明顯看出，當t1= 200 時，液艙中液體晃蕩高度分別為30、18 和15 左右;當t1=400 時，晃蕩高度分別達到60、35 和30 左右。由此可見，在輸入頻率為橫蕩方向外部激發頻率與縱蕩方向的固有頻率的和頻時，液體深度越大，其二階共振晃蕩的振幅就越小。而與圖6(a)～(c)所反映的輸入頻率為縱蕩方向外部激發頻率與橫蕩方向固有頻率的和頻的情況進行比較，兩者二階共振的變化規律正好相反。

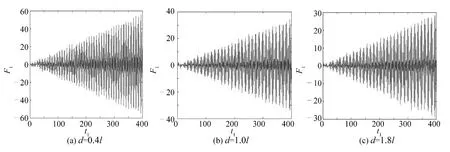
圖8 不同液深情況F1 相對于t1 的變化Fig.8 F1 against t1 in the case of different water depths in tank as Ω2 + ω1 = ω11

當Ω2－ ω1= ω11時，根據d = 0.4l、d = l、d = 1.8l 三種液體深度情況下，液艙晃蕩二階共振的液面高度隨時間變化的曲線可以得到，當t1= 200 時，液艙中液體晃蕩高度分別為130、120 和110 左右;當t1=400 時，晃蕩高度分別達到280、260 和220 左右。由此可見，在輸入頻率為橫蕩方向外部激發頻率與縱蕩方向的固有頻率的差頻時，液體深度越大，其二階共振晃蕩的振幅就越小。相對于輸入和頻，在此輸入頻率時，液深的變化對二階共振振幅的影響相對比較小。

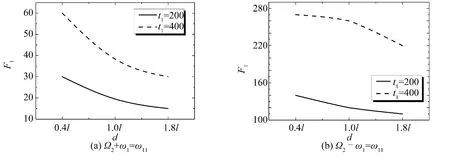
圖9 當t1 一定時不同液深情況下F1 的變化Fig.9 F1 against the water depth in tank at t1 = 200 and t1 = 400 ，respectively

由圖9(a)可以看出，其曲線變化趨勢與圖5(a)大體一致。但無量綱波高值不大，說明此時液艙內液面晃蕩現象并不明顯。由圖9(b)可以看出，曲線下降很緩，這說明對于差頻二階共振晃蕩振幅隨著液深的變化并不明顯。

3 結 語

推導了液艙三維晃蕩運動二階共振問題的理論解，并討論了其特性。在二維的條件下，當外部激發頻率的和頻或者差頻等于液艙偶模固有頻率時，二階共振就會發生。對于三維問題，當在縱搖和橫搖運動中都存在激發頻率，則縱搖和橫搖之間的耦合運動在二階共振中起著非常重要的作用。當縱蕩和橫蕩兩個晃蕩方向的和頻或者差頻等于液艙奇模固有頻率時，就會發生二階共振。當某一晃蕩方向(橫蕩或縱蕩)外部激發頻率與另一方向(縱蕩或橫蕩)液艙某一固有頻率的差值或和等于液艙另一固有頻率時，也會發生二階共振。

通過數值模擬簡要地分析了各個激發頻率下不同液深對共振振幅的影響。分析可得，對于兩個晃蕩方向外部激發頻率的和頻、或單一晃蕩方向(縱蕩或橫蕩)某一個激發頻率與另一晃蕩方向(橫蕩或縱蕩)某一個屬于奇模的固有頻率的和頻引發的共振情況，水深變化對共振的振幅大小影響比較大;而對于兩個晃蕩方向外部激發頻率的差頻、或單一晃蕩方向(縱蕩或橫蕩)某一個激發頻率與另一晃蕩方向(橫蕩或縱蕩)某一個屬于奇模的固有頻率的差頻引發的共振情況，水深變化對共振的振幅大小影響比較小。

應當指出的是，二階共振振幅與激發振幅的平方有關。文獻［20-21］證明了粘性對晃蕩共振的影響會在激發振幅對晃蕩共振的影響起作用之前就已經明顯了。這表明激發振幅和粘性對晃蕩共振的影響也是很明顯的。目前的工作可以進一步擴展到研究沿水深具有不同密度液體的晃蕩問題。

［1］ISSC T C-2，Dynamic load effect［S］.ISSC Proceedings，1991.

［2］ISSC T C-2，Dynamic load effect［S］.ISSC Proceedings，1994.

［3］朱仁慶，侯玲.LNG 船液艙晃蕩數值模擬［J］.江蘇科技大學學報:自然科學版，2010，24(1):1-6.(ZHU Renqing，HOU Ling.Numerical simulation of liquid sloshing in the tanks of LNG carrier［J］.Journal of Jiangsu University of Science and Technology，Natural Science Edition，2010，24(1):1-6.(in Chinese))

［4］FALTINSEN O M.A numerical non-linear method for sloshing in tanks with two dimensional flow［J］.Journal of Ship Research，1978，18(4):224-241.

［5］WU G X，MA Q W，EATOCK T R.Numerical simulation of sloshing waves in a 3D tank based on a finite element method［J］.Applied Ocean Research，1998，20:337-355.

［6］WANG C Z，KHOO B C.Finite element analysis of two-dimensional nonlinear sloshing problems in random excitation［J］.Ocean Engineering，2005，32:107-133.

［7］HUANG H C，WANG C Z，LENG J X.Fully nonlinear simulations of wave resonance by an array of cylinders in vertical motions［J］.Chine Ocean Engineering，2013，27(1):87-98.

［8］FALTINSEN O M，TIMOKHA A N.An adaptive multimodal approach to nonlinear sloshing in a rectangular tank［J］.Journal of Fluid Mechanics，2001，432:167-200.

［9］HU P X，WU G X，MA Q W.Numerical simulation of nonlinear wave radiation by a moving vertical cylinder［J］.Ocean Engineering，2002，29:1733-1750.

［10］MA Q W，WU G X，EATOCK T R.Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves.Part 1:Methodology and numerical procedure［J］.International Journal for Numerical Methods in Fluids，2001，36:265-285.

［11］MA Q W，WU G X，EATOCK T R.Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves.Part 2:Numerical results and validation［J］.International Journal for Numerical Methods in Fluids，2001，36:287-308.

［12］張雨新，萬德成，日野孝則.MPS 方法數值模擬液艙晃蕩問題［J］.海洋工程，2014，32(4):24-32.(ZHANG Yuxin，WAN Decheng，HINO Takanori.Application of MPS method in liquid sloshing［J］.The Ocean Engineering，2014，32(4):24-32.(in Chinese))

［13］WU G X.Second-order resonance of sloshing in a tank［J］.Ocean Engineering，2007，34:2345-2349.

［14］WANG C Z，WU G X，KHOO B C.Fully nonlinear simulation of resonant motion of liquid confined between floating structures［J］.Computers and Fluids，2011，44:89-101.

［15］CHERN M J，VAZIRI N，BORTHWICK A G L.Fully non-linear simulation of second-order resonance in a three-dimensional tank using the PSME method［J］.Applied Ocean Research，2012，37:22-32.

［16］CHERN M J，VAZIRI N，SYAMSURI S，et al.Pseudospectral solution of three-dimensional nonlinear sloshing in a shallow water rectangular tank［J］.Journal of Fluids and Structures，2012，35:160-184.

［17］WANG C Z，WU G X.Time domain analysis of second-order wave diffraction by an array of vertical cylinders［J］.Journal of Fluids and Structures，2007，23:605-631.

［18］WANG C Z，WU G X.Analysis of second-order resonance in wave interactions with floating bodies［J］.Ocean Eng.，2008，35:717-726.

［19］黃碩，段文洋，馬慶位，等.液艙晃蕩及其與船舶耦合運動問題的研究進展［J］.船舶力學，2013，17(10):1209-1220.(HUANG Shuo，DUAN Wenyang，MA Qingwei，et al.Research progress on sloshing and coupling motion of sloshing and ship［J］.Journal of Ship Mechanics，2013，17(10):1029-1220.(in Chinese))

［20］WU G X，EATOCK T R，GREAVES D M.Viscous effect on the transient free surface flow in a two dimensional tank［J］.J.Eng.Math.，2001，40:77-90.

［21］WU G X.Sloshing of stratified liquid in a two dimensional rectangular tank［J］.Science of China，2011，54:2-9.