Dynamic Surface Control with Nonlinear Disturbance Observer for Uncertain Flight Dynamic System

Li Fei（李飛），Hu Jianbo（胡劍波），Wu Jun（吳俊），Wang Jianhao（王堅浩）

1.Equipment Management and Safety Engineering College，Air Force Engineering University，Xi＇an 710051，P.R.China；

2.Institute of Cyber-Systems and Control，Zhejiang University，Hangzhou 310027，P.R.China；

3.Unit 93286，People＇s Liberation Army，Shenyang 110141，P.R.China

Dynamic Surface Control with Nonlinear Disturbance Observer for Uncertain Flight Dynamic System

Li Fei（李飛）1*，Hu Jianbo（胡劍波）1，Wu Jun（吳俊）2，Wang Jianhao（王堅浩）3

1.Equipment Management and Safety Engineering College，Air Force Engineering University，Xi＇an 710051，P.R.China；

2.Institute of Cyber-Systems and Control，Zhejiang University，Hangzhou 310027，P.R.China；

3.Unit 93286，People＇s Liberation Army，Shenyang 110141，P.R.China

A new robust control method of a nonlinear flight dynamic system with aerodynamic coefficients and external disturbance has been proposed.The proposed control system is a combination of the dynamic surface control（DSC）and the nonlinear disturbance observer（NDO）.DSC technique provides the ability to overcome the＂explosion of complexity＂problem in backstepping control.NDO is adopted to observe the uncertainties in nonlinear flight dynamic system.It has been proved that the proposed design method can guarantee uniformly ultimately boundedness of all the signals in the closed-loop system by Lyapunov stability theorem.Finally，simulation results show that the proposed controller provides better performance than the traditional nonlinear controller.

nonlinear disturbance observer（NDO）；dynamic surface control（DSC）；uncertainties；flight control

Nomenclature

F Aerodynamic forces about the body-fixed frame

L，M，N Aerodynamic rolling，pitching，yawing moments

1 Moment of inertia

p，q，r Roll，pitch，yaw rates about the bodyfixed frame

ˉq Dynamic pressure

T Thrust

V Velocity

α，β Angle of attack，sideslip angle

δe，δa，δrElevator，aileron，rudder angles

φ，θ Roll，pith angles

0 Introduction

With the fast development of aerospace engineering technology over the past few decades，the modern flight vehicles has become more and more sophisticated and complex in order to fulfill the growing requirements for safety，performance and autonomy challenges.Specific interests have been paid to flight dynamic systems due to unknown disturbances existing widely in aerospace engineering，such as wind，friction，coupling effects from other systems，environmental and electromagnetic noise，etc.Therefore，it is crucial for a nonlinear control method to handle unknown disturbances，as well as to be robust against unmodeled dynamics and variation of various aerodynamic derivatives［1-2］.

Feedback linearization is probably the most common method employed in nonlinear flight control［3-4］without state transformation.Since it needs complete and accurate knowledge of the plant dynamics，an adaptive backstepping design methods is proposed［5-6］.However，the parameter estimation error is only guaranteed to be bounded and converging to an unknown constantvalue.Dynamic surface control（DSC）technique can overcome the problem of complexity in backstepping design resulting from the repeated differentiations by introducing a first-order filtering of the synthetic input at each step［7-8］.Nonlinear disturbance observer（NDO）effectively rejects model mismatches and external disturbances to compensate timely for the controller by constructing a new dynamic system［9-11］.Hence it can improve the performance of the controller by eliminating the effects of uncertainties of controlled device.NDO has been widely applied to robot control［10-13］，missile control［14］，flight control［15-16］and so on.

Accordingly，a new robust control design method for nonlinear flight dynamic system with aerodynamic coefficients and external disturbances is proposed in this paper.Firstly，the nonlinear flight model is presented with aerodynamic coefficients and external disturbances.Secondly，the design principles of nonlinear disturbance observer are introduced，and the structure of the composite controller is investigated.Moreover，the stability of the proposed control system is analyzed.Finally，simulation results demonstrate that the proposed controller could effectively resist the influence of uncertainties and disturbances on the flight control system.

1 Problem Description

The control law design is based on the nonlinear model of an F-16 fighter.The controller is to track the commands ofα，β，andφwhen there exist parameter perturbations and external disturbance.The relevant equations of six-degree nonlinear model used for the control design can be written as［17］

The flight dynamic Eqs.（1—7）can be rearranged as an uncertain non-linear multiple-input multiple-output（MIMO）system considering the external disturbance and aerodynamic coefficient perturbations.

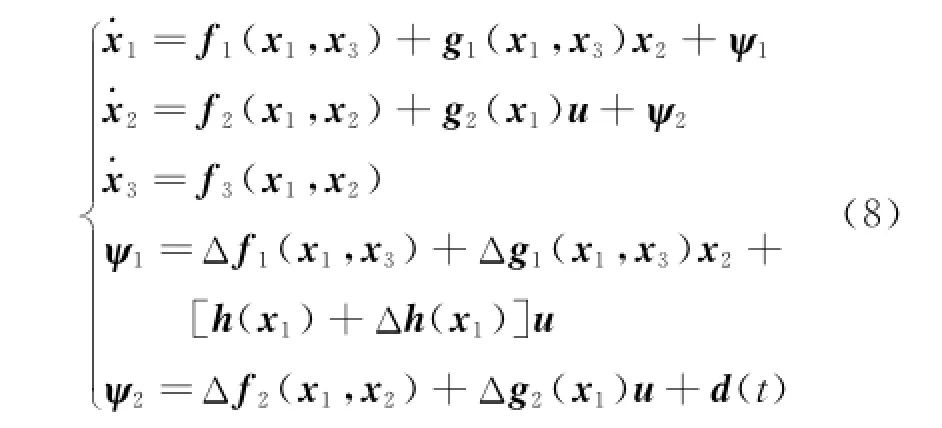
where x，u，f，g，h represent the following parameters，respectively，and x1=［α，β，φ］T，x2=［p，q，r］T，x3=［θ，ψ］T，u=［δe，δa，δr］T.

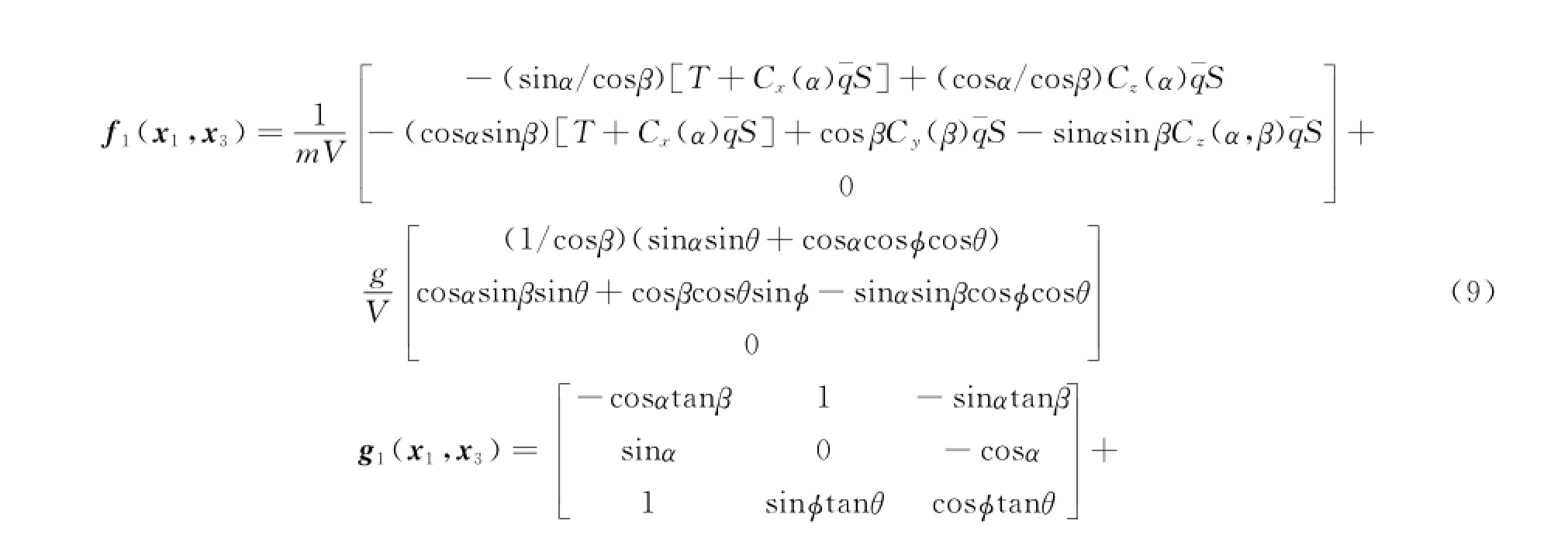
whereψ1andψ2are the compound uncertainties in the model，Δf（x），Δg（x），Δh（x）the aerodynamic coefficients，and d（t）the external disturbance.

The following assumptions are adopted in the design and analysis processes.

Assumption 1 The desired trajectory yc=［αc，βc，φc］Tis bounded as

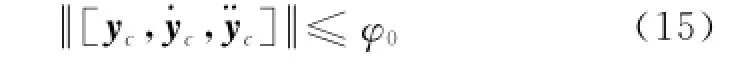
whereφ0∈R is a known positive constant and‖·‖denotes the 2-norm of a vector or a matrix.

Assumption 2 The total velocity and dynamic pressure are constant.

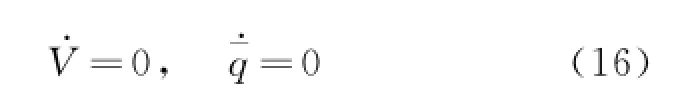
Remark 1 Note that g2represents the input matrix of the control u to the dynamics of the angular rates p，q and r.Since the control surfaces of the aircraft are designed to control each axes＇angular rate of aircraft independently，the input matrix g2is invertible for all cases.

Remark 2 Note that h1is the aerodynamic force component caused by the control surface deflection.The magnitude of h1is small，compared to other aerodynamic terms in the dynamic equation［17］.Therefore，it can be assumed that h1is one part of model uncertainties.

2 Nonlinear Disturbance Observer

The dynamic surface control law is designed by separating the flight dynamics into fast and slow dynamics［17］.So here NDOs are designed in the inner and the outer loops respectively［13，15］.

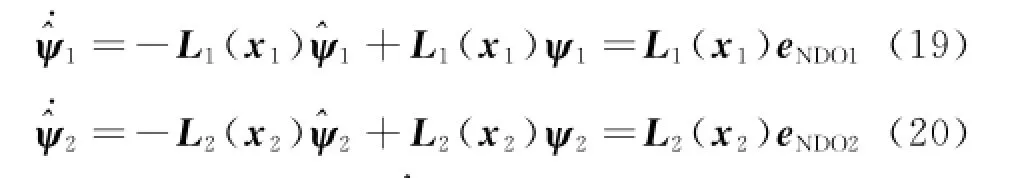
It is assumed that the uncertainties are slowly time-varying compared with the dynamics of NDO.Consequently，.ψ1≈0，.ψ2≈0.

Then Eqs.（19，20）can be rewritten as

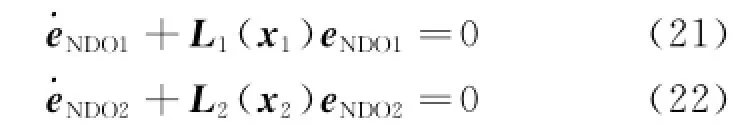
To avoid the angular acceleration measurement，an auxiliary nonlinear function vector is defined to improve the NDO in the inner loop.

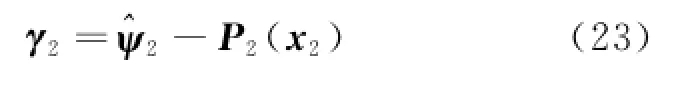
where

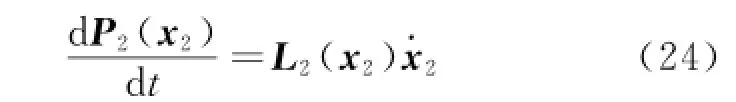
From Eq.（23），one has

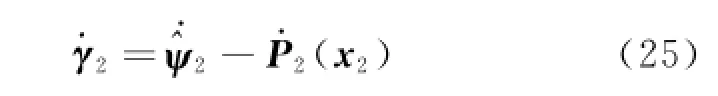
From Eqs.（20，24），the derivative ofγ2can be expressed as

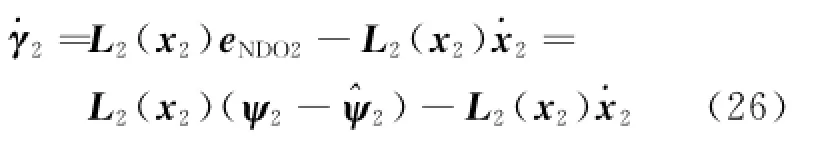
From Eq.（8），Eq.（26）can be rewritten as

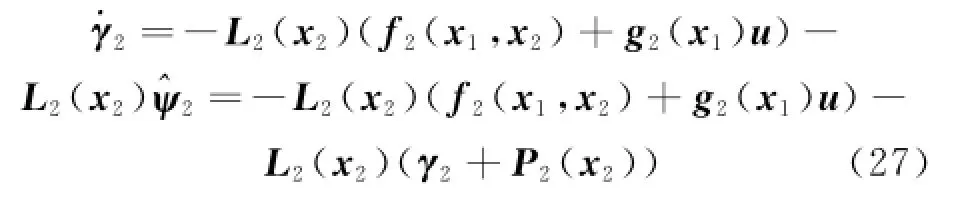
Hence NDO in the inner loop of the flight dynamic system can be designed as

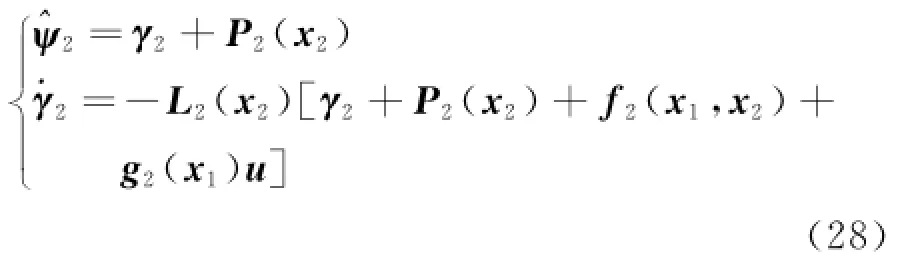
Remark 3 From the dynamics of NDO Eqs.（19，20），the output of NDOs?ψ1and?ψ2will converge toψ1andψ2via choosing appropriate values of L1（x1）and L2（x2）.

3 Controller Design

The structure of the two-timescale controller for flight control system is shown in Fig.1.In each feedback loop，control laws x2cand u are designed separately.

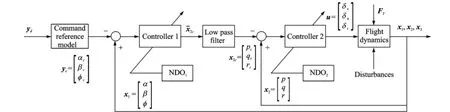
Fig.1 Structure of the two-timescale controller

The dynamic surface control method is used to design a controller here.The dynamic surface control method can be viewed as the twotimescale approach because the fast state x2is used as control input for the slow state x1intermediately.However，this methodology considers the transient responses of the fast states and，therefore，does not require the timescale separation assumption.

The controller design procedure can be given as follows.

Step 1 Define error surface S1=x1-x1c， where x1c=yc.Its derivative is

where x2cis the expected virtual control of the inner loop，e2=x2-x2c.From Eq.（17），one has .S1=f1+g1（x2c+e2）+?ψ1+eNDO1-.yc（30）

One chooses the virtual control as

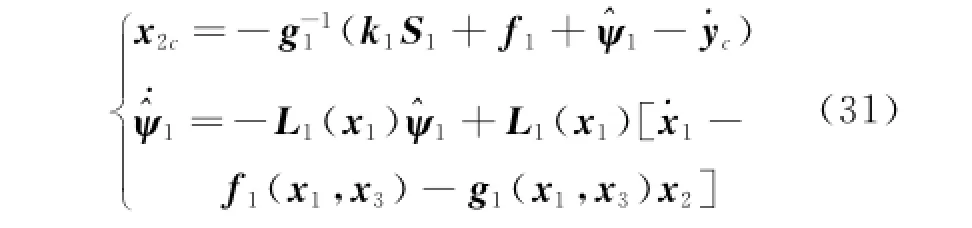
The parameter x2cpasses through a firstorder filter with time constantτ2＞0 to obtain the filtering virtual controlˉx2c，which can solve the computational complexity in each step.

Therefore

Step 2 Defining the error surface S2=x2-，its derivative is

The NDO（Eq.（28））is used to observe the uncertaintyψ2in the inner loop.

Choose an actual control u to drive S2→0 as follows

4 Stability Analysis

The derivative of the surface errors to represent the closed-loop system is described as follows

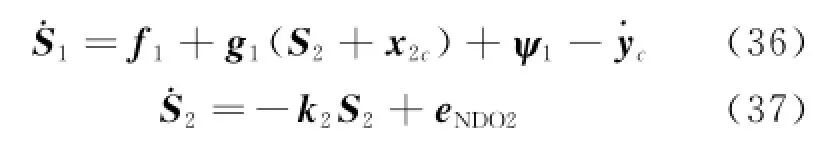
Then，the boundary error is defined as

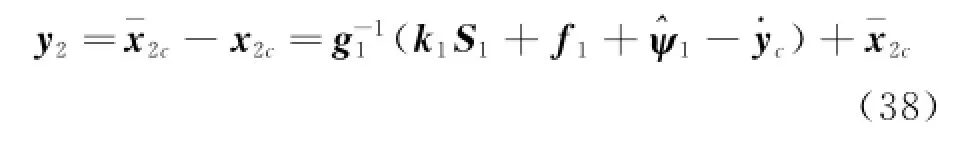
Using Eqs.（17，38），Eq.（36）can be rewritten as

Differentiating Eq.（38），one can obtain

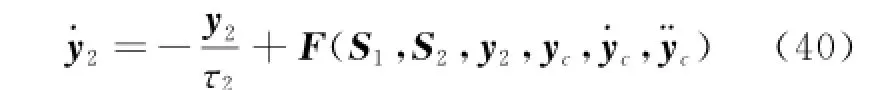
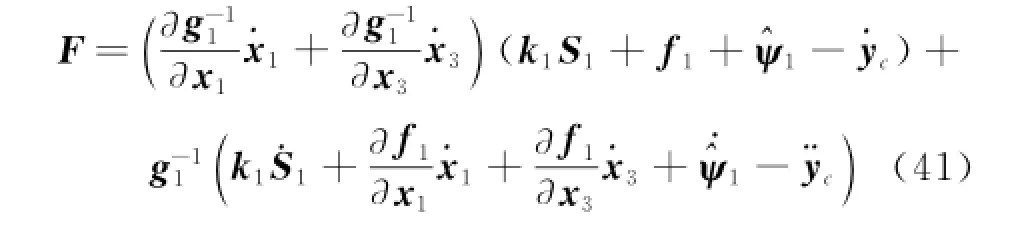
where And F is continuous.

Consider the following Lyapunov function candidate

Assumption 4 Assume that the Lyapunov candidate function Eq.（42）is bounded by any given positive numberλ，i.e.，V≤λ.

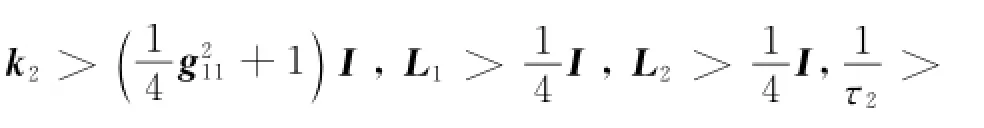
Differentiating the Lyapunov candidate function Eq.（42）and substituting Eqs.（21，22，37，39，40），one can obtain

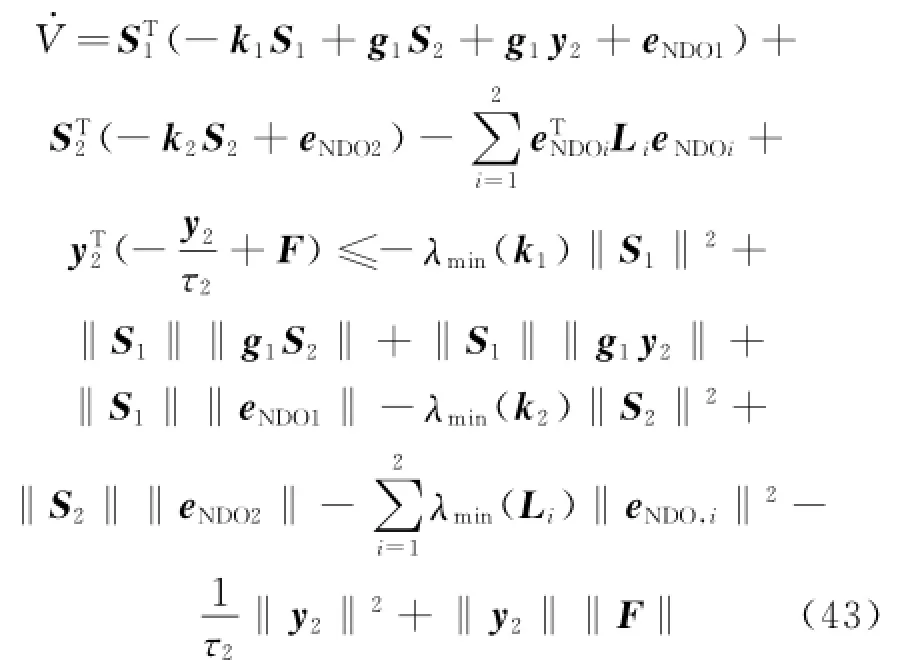
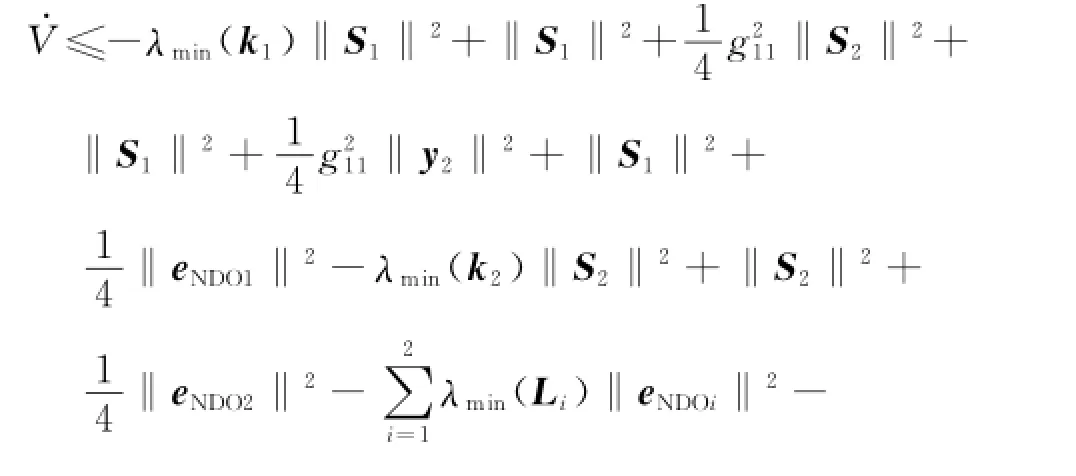
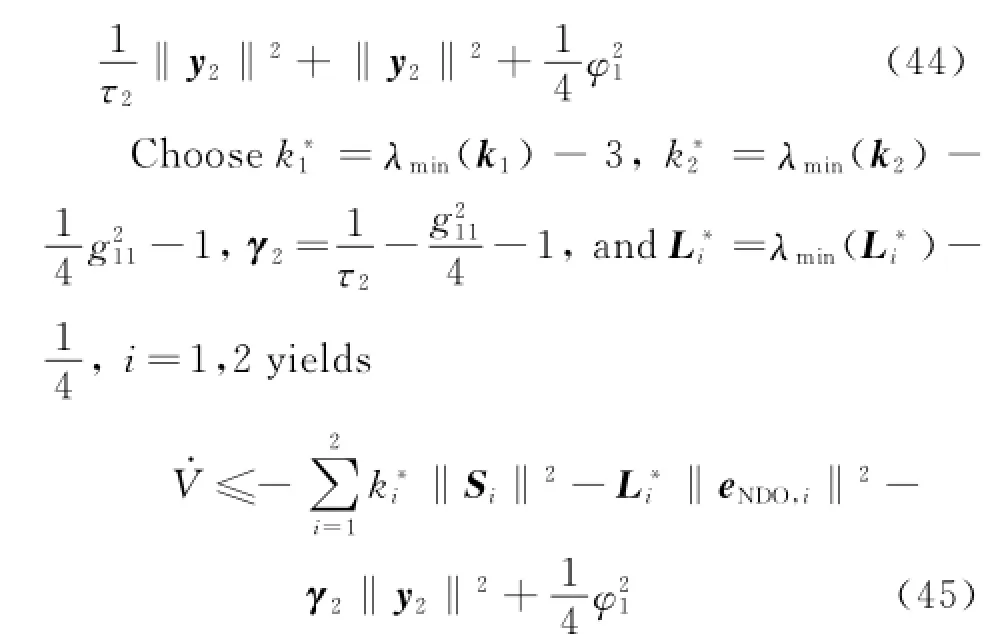
where k*i＞0，L*i＞0，γ2＞0.

Then，choose the constantμthat satisfies the following condition

Hence，Eq.（30）can be rewritten as

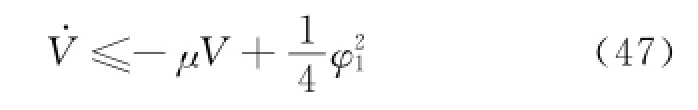
The integration of Eq.（45）is multiplied by e-μt.

Accordingly，the surface errors S1and S2，the nonlinear disturbance observer errors eNDO1and eNDO2，the boundary layer error y2are uniformly ultimately bounded in the following compact set Ω.

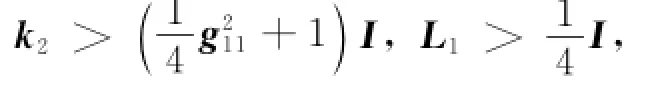
5 Simulation Results

The simulation results are presented from the application of the nonlinear disturbance observer-enhanced dynamic surface flight control approach.The proposed controller is tested in simulation on the attitude maneuver flight control system of F-16 aircraft.The following command values ofαd，βd，andφdare applied to the aircraft in a steady-state level flight of V=200 m/s，h= 4 000 m，FT=60 k N.

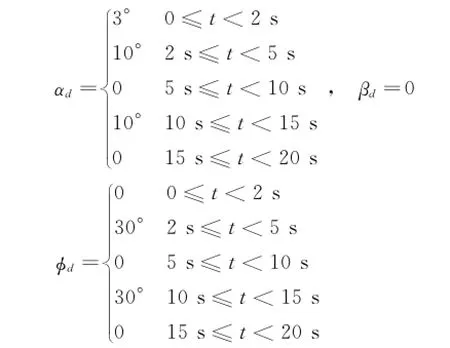
The parameter yccan be obtained from ydby the following command filter

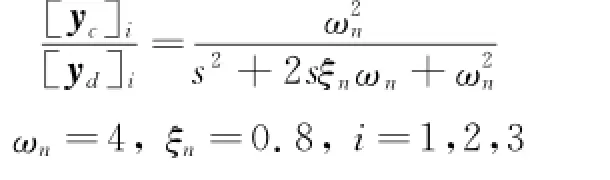
It is assumed that the uncertainties are timevarying.The time-varying aerodynamic coefficients and external disturbance are given as

Cj=［1+0.5sin（0.5πt）］Crjj=x，y，z，l，m，n d（t）=［0.5 1 1.5］×104sin（t）

The final design parameters are chosen as l1=10I，l2=5I，τ2=0.05，where I represents the 3×3 identity matrix.Nonlinear disturbance observer gains are chosen as

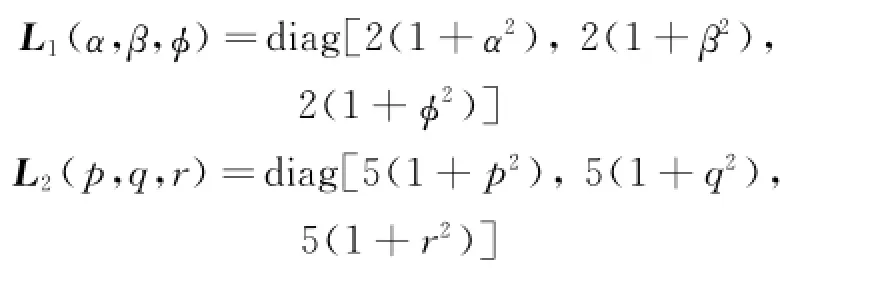
Simulation resultsareshown in Figs.2—7.

Fig.2 Attacking angle trackingα

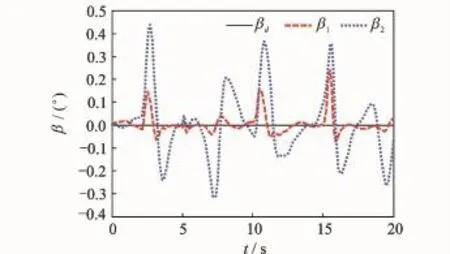
Fig.3 Sideslip angle trackingβ

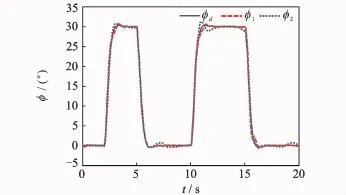
Fig.4 Rolling angle trackingφ

Fig.5 Roll rate tracking p

Fig.6 Pitching rate tracking q

The subscripts＂1＂＂2＂represent the simulation results of dynamic surface controller with and without NDO，respectively.Figs.2—7 show that under uncertainties，the proposed NDO-enhanced dynamic surface control method performs better and can guarantee the boundedness of the signals in a closed-loop system.

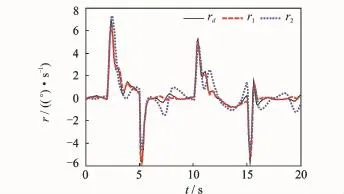
Fig.7 Yawing rate tracking r

6 Conclusions

A nonlinear disturbance observer-enhanced dynamic surface flight control approach for nonlinear flight dynamic system with aerodynamic coefficients and external disturbance uncertainties has been proposed.The approach can solve the problem of＂explosion of complexity＂caused by the traditional backstepping method and exhibits the excellent disturbance attenuation ability and robustness against uncertainties.All the signals in the closed-loop system are guaranteed to be globally and uniformly bounded ultimately.And the tracking error of the system is proven to converge to a small neighborhood of the origin.The dynamic surface control with the NDO approach proposed in this paper may also be used in the design of the controllers for other dynamic systems with model mismatches and external disturbance.

Acknowledgements

This work was supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology Zhejiang University China（No.ICT1401）and Shanghai Leading Academic Discipline Project（No. J50103）.

［1］ Qiao B，Liu Z Y，Hu B S，et al.Adaptive angular velocity tracking control of spacecraft with dynamic uncertainties［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2014，31（1）：85-90.

［2］ Wu W H，Gao L，Mei D，et al.Adaptive controller for aircraft attitude with input constraints［J］.Journal of Nanjing University of Aeronautics&Astronautics，2012，44（6）：809-816.（in Chinese）

［3］ Ur R O，Petersen I R，Fidan B.Feedback linearization-based robust nonlinear control design for hypersonic flight vehicles［J］.Proceedings of the Institution of Mechanical Engineers，2013，227（1）：3-11.

［4］ Li D D，Sun X X，Dong W H，et al.Pitch control for flight in heavy-weight airdrop based on feedback linearization theory and variable-structure control［J］. Control Theory and Applications，2013，30（1）：54-60.（in Chinese）

［5］ Sonneveldt L，Chu Q P，Mulder J A，Nonlinear flight control design using constrain adaptive backstepping［J］.Journal of Guidance，Control，and Dynamics，2007，30（2）：322-336.

［6］ Mei R，Wu Q X，Jiang C S.Robust adaptive backstepping control for a class of uncertain nonlinear systems based on disturbance observers［J］.Science China Information Sciences，2010，53（6）：1201-1215.

［7］ Yoo S J.Adaptive track and obstacle avoidance for a class mobile robots in the presence of unknown skidding and slipping［J］.IET Control Theory and Applications，2011，5（14），pp.1597-1608.

［8］ Sung J Y，Park J B，Choi Y H.Adaptive dynamic surface control of flexible-joint robots using selfrecurrent wavelet neural networks［J］.IEEE Trans Syst，Man，Cybern B，2006，36（6）：1342-1355.

［9］ Liu C，Li Y H，Zhu X H.Adaptive sliding mode observe for actuator fault reconstruction in nonlinear system with mismatched uncertainties［J］.Control Theory and Application，2014，31（4）：431-437.（in Chinese）

［10］Dong W，Gu G Y，Zhu X Y，et al.High-performance trajectory tracking control of a quadrotor with disturbance observer［J］.Sensors and Actuators，2014（A211）：67-77.

［11］Wei X J，Chen N，Li W Q.Composite adaptive disturbance observer-based for a class of nonlinear systems with multisource disturbance［J］.International Journal of Adaptive Control and Signal Processing，2013，27：199-208.

［12］Nikoobn A，Haghighi R.Lyapunov-based nonlinear disturbance observer for serial n-link robot manipulators［J］.IEEE Transactions on Industrial Electronics，2009，55（2）：135-153.

［13］Liu X，Huang Q，Chen Y.Adaptive control with disturbance observer for uncertain teleoperation systems［J］.Control Theory and Applications，2012，29（5）：681-687.（in Chinese）

［14］Li S H，Yang J.Robust autopilot design for bank-toturn missiles using disturbance observers［J］.IEEE Transactions on Aerospace and Electronic Systems，2013，49（1）：558-579.

［15］Zhang T Y，Zhou J，Guo J G.Design of predictive controller for hypersonic vehicles based on disturbance observer［J］.Acta Aeronautica et Astronautica Sinica，2014，35（1）：215-222.（in Chinese）

［16］Chen M，Zou Q Y，Jiang C S，et al.Dynamical inversion flight control based on the neural network disturbance observer［J］.Control and Decision，2008，23（3）：283-287.（in Chinese）

［17］Lee T Y，Kim Y D.Nonlinear adaptive flight control using backstepping and neural networks controller［J］.Journal of Guidance，Control，and Dynamics，2001，24（4）：675-682.

（Executive editor：Zhang Tong）

*Corresponding author：Li Fei，Engineer，E-mail：lizhaodi726@163.com.

How to cite this article：Li Fei，Hu Jianbo，Wu Jun，et al.Dynamic surface control with nonlinear disturbance observer for uncertain flight dynamic system［J］.Trans.Nanjing U.Aero.Astro.，2015，32（4）：469-476.

http：//dx.doi.org/10.16356/j.1005-1120.2015.04.469

（Received 17 July 2014；revised 19 November 2014；accepted 24 November 2014）

TP273 Document code：A Article ID：1005-1120（2015）04-0469-08