大氣湍流對高斯光束瑞利區間的影響

王 慧,楊 軍,章 曦

(解放軍理工大學理學院,江蘇 南京 211101)

?

·光學技術·

大氣湍流對高斯光束瑞利區間的影響

王 慧,楊 軍,章 曦

(解放軍理工大學理學院,江蘇 南京 211101)

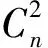
瑞利區間;高斯光束;大氣湍流;Andrews修正譜;Von Karman譜

1 引 言

激光束在大氣中傳輸時由于受到大氣湍流的影響,易發生光強閃爍、波前失真以及光束快速擴展等現象,從而限制了激光的實際應用。大氣湍流還可以使得激光光束的相干性發生退化[1]。1990年,Wu[2]從理論上證明了部分空間相干光受大氣湍流的影響比完全相干光受到的影響小。2002年,Gbur等[3]給出了部分空間相干光受大氣湍流影響的條件,并得到了Dogariu等[4]的實驗驗證。考慮到大氣湍流的隨機性,可以運用大氣折射率起伏功率譜密度模型來描述大氣湍流的特征,本文主要采用L.C.Andrews修正譜(M譜),并將計算結果與Von Karman譜的計算結果進行對照。在激光理論中,瑞利區間表示完全相干激光光束無明顯擴展的傳輸距離,后來Gbur等[3]把這一概念拓展到部分相干光,最近激光束瑞利區間的概念進一步從自由空間拓展到大氣湍流中,大氣湍流使得激光光束瑞利區間縮短,湍流越強瑞利區間越短[5]。本文根據部分相干雙曲余弦高斯光束在自由空間和湍流大氣中傳輸光束瑞利區間的解析結果,采用M譜進行數值分析,研究了大氣湍流的尺寸效應、相干參數、光束參數、大氣湍流內尺度、束腰寬度和折射率起伏結構常數等對部分相干雙曲余弦高斯光束在自由空間和實際空間中傳輸的影響,并將結果與其他相關研究工作進行對比[6-7],為實際應用提供參考。

2 理論模型

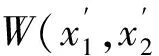
其中:

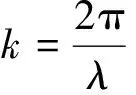
在自由空間中,瑞利區間ZRfree定義為光束橫截面積擴展到源場處面積的兩倍時光束所傳輸的距離。因此部分相干雙曲余弦高斯光束通過自由空間傳輸的瑞利區間為:

(1)

根據文獻[11-12]可知,在大氣湍流中部分相干光的二階矩x2可寫為:

(2)

3 數值計算結果與分析

大氣折射率起伏功率譜模型的選取非常重要[13],本文主要采用適用于各種強度湍流大氣的M譜,即:

(3)

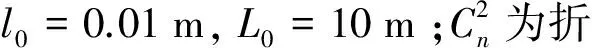
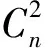
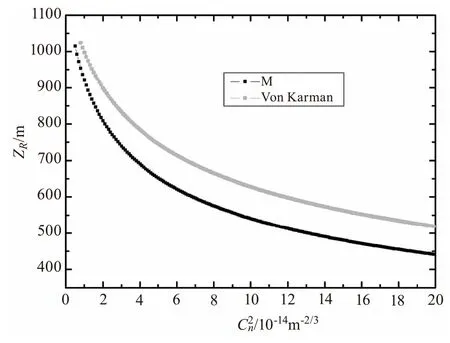
圖1 ZR隨變化關系圖(ω0=0.02m,α=1,β=1,λ=1.06 μm)

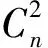
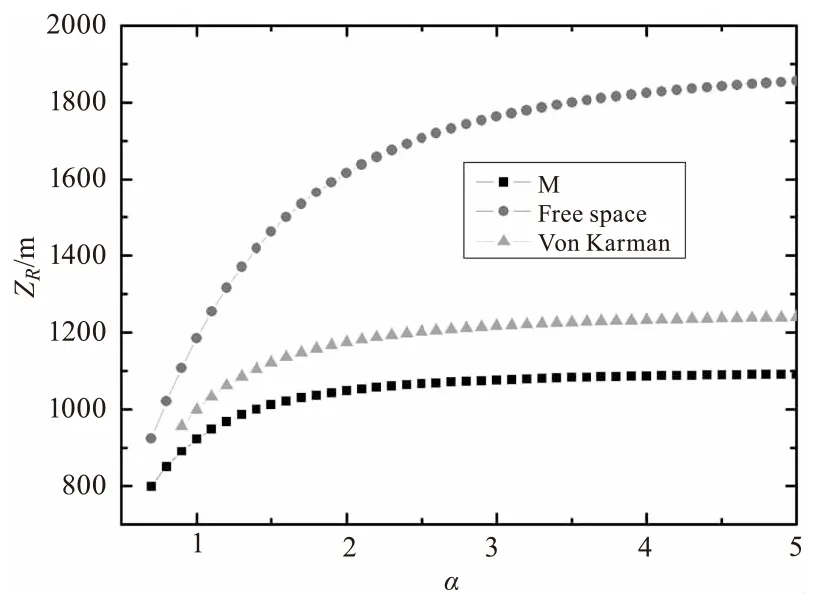
圖2 ZR隨α變化關系圖(ω0=0.02 m,β=1,

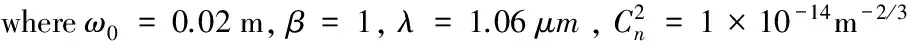
圖2 給出了Von Karman譜和M譜的瑞利區間ZR隨光束相干參數α變化關系曲線,作為對比同時給出了自由空間的瑞利區間。從圖2中可以看出,相比于自由空間,大氣湍流的存在大幅度降低了激光傳輸的瑞利區間,瑞利區間ZR隨相干參數α的增加而增加,但當α>2時,曲線斜率明顯減小,說明繼續增加光束的相干性對提高瑞利區間ZR影響較小。同樣,Von Karman譜和M譜對瑞利區間隨光束相干參數α變化的影響趨勢相同,但是M譜計算得出的瑞利區間比相同條件下Von Karman譜計算得出的瑞利區間稍小。

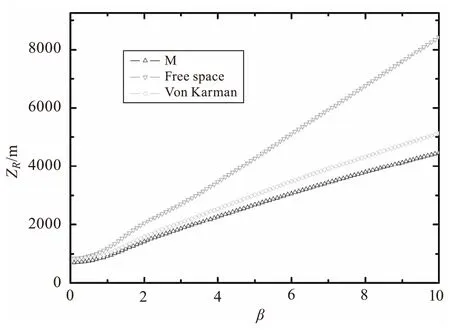
圖3 ZR隨β變化圖(ω0=0.02 m,α=1,

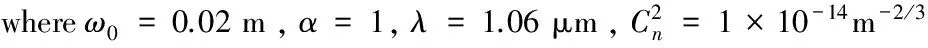
圖3 是Von Karman譜和M譜的瑞利區間ZR隨光束參數β變化曲線,從圖中可以看出,瑞利區間ZR隨光束參數β的增加而增加,特別當β>2則近似于線性增加,說明激光傳輸過程中的光束參數和束腰寬度都對瑞利區間的變化影響顯著,在實際應用中,應該盡可能提高光束參數的大小以利于瑞利區間的增加,提高通信質量。

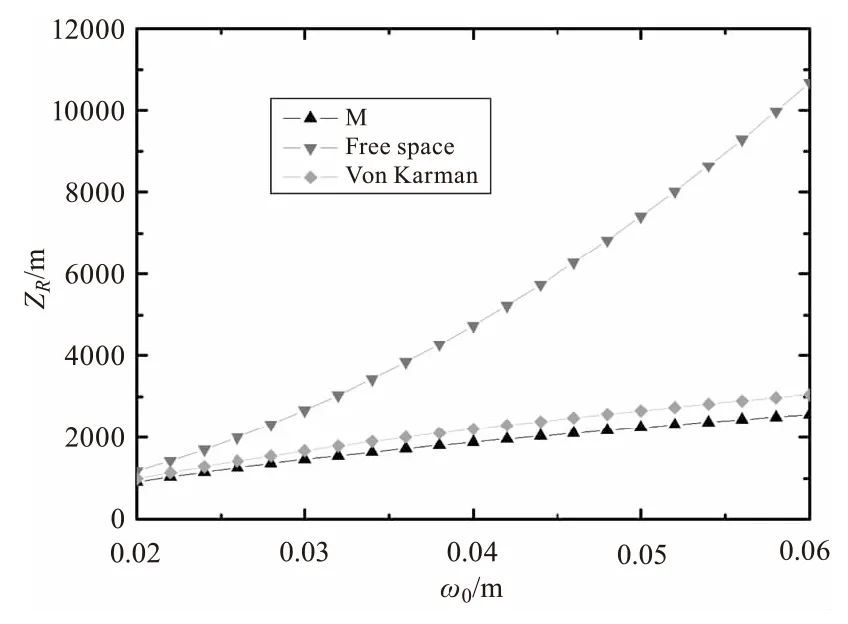
圖4 ZR隨ω0變化關系圖(α=1,β=1,

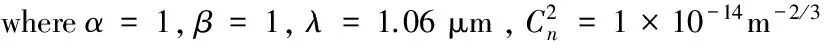
圖4 給出的是Von Karman譜和M譜的瑞利區間ZR隨束腰寬度w0變化曲線,圖中可以看出,在自由空間中,瑞利區間隨高斯束寬的增加而顯著增大,但在實際空間中,瑞利區間仍然呈現出增加的趨勢,但增加趨勢明顯降低,所以增加束腰寬度對激光的相位保持是有利的。

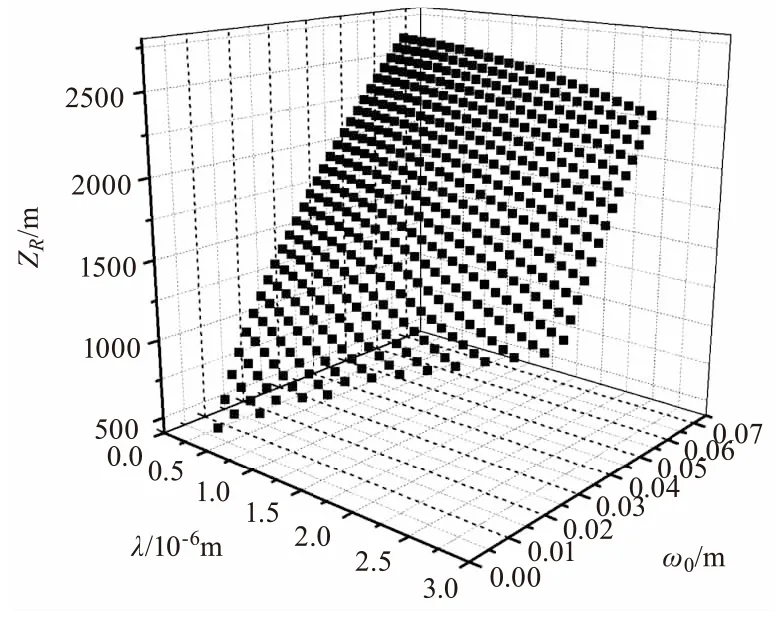
圖5 ZR隨λ與ω0變化關系圖

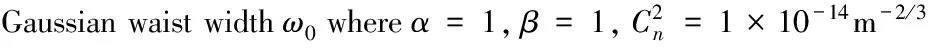
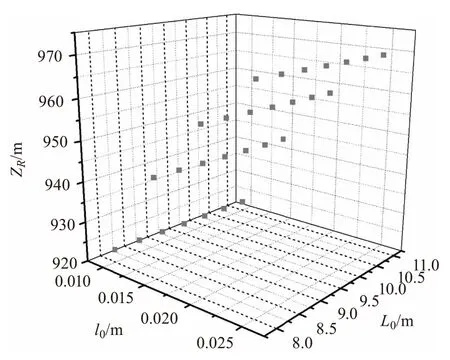
圖6 ZR隨L0與l0變化關系圖(α=1,β=1,

圖5和圖6給出了瑞利區間隨湍流尺寸及激光波長的對應關系。圖5表明波長λ越小、束腰寬度ω0越大,瑞利區間ZR越大。光束波長越小,則光子的能量越大,其受散射作用相對越弱,因此瑞利區間越大。因此實際應用中可以通過提高相干參數α、提高光束參數β、增加束腰寬度ω0以及減小光束波長λ來提高瑞利區間ZR。圖6表明瑞利區間ZR受湍流外尺度L0變化的影響較小,而受湍流內尺度l0變化的影響較大,湍流內尺度l0越大,瑞利區間ZR越大,表現出明顯的尺寸效應。大氣湍流內尺度在地面附近的典型測量結果是幾個毫米,并且隨高度的增加而增加,最大能夠達到幾十厘米,因此選擇湍流內尺度較大的區域有利于提高瑞利區間。

4 結 論

[1] Ji X L,Eyyuboglu H T,Baykal Y.Influence of turbulence on the effective radius of curvature of radial Gaussian array beams[J].Opt.Express,2010,18(7):6922-6928.

[2] Wu J.Propagation of a Gaussian-Schell beam through turbulent media[J].J.Mod.Opt,1990,37:671-684.

[3] Gbur G,Wolf E.Spreading of partially coherent beams in random media[J].J.Opt.Soc.Am.A,2002,19:1592-1598.

[4] Dogariu A,Amarande S.Propagation of partially coherent beams:turbulence-induced degradation[J].Opt.Lett,2003,28:10-12.

[5] JI Xiaoling.Influence of the atmosphericc turbulence on propagation properties of laser beams[J].Journal of Sichuan Normal University:Nature Science,2012,35:127-136.(in Chinese)

季小玲.大氣湍流對激光束傳輸特性的影響[J].四川師范大學學報:自然科學版,2012,35:127-136.

[6] JI Xiaoling.Influence of turbulence on the Payleigh range of partially coherent cosh-Gaussian beams[J].Acta Phys.Sin.,2011,60:064207.(in Chinese)

季小玲.湍流對部分相干雙曲余弦高斯光束的瑞利區間的影響[J].物理學報,2011,60:064207.

[7] LI Jinhong,Lü Baida.Comparative study of partially coherent vortex beam propagations through atmospheric turbulence along an uplink path and a downlink path[J].Acta Phys.Sin.,2011,60:074205.(in Chinese)

李晉紅,呂百達.部分相干渦旋光束通過大氣湍流上行和下行傳輸的比較研究[J].物理學報,2011,60:074205.

[8] Casperson L W,Tovar A A.Hermite-sinusoidal-Gaussian beams in complex optical systems[J].J.Opt.Soc.Am.A,1998,15(4):954-961.

[9] Zahid M,Zubairy M S.Directionality of partially coherent Bessel-Gauss beams[J].Opt Comm,1989,70(5):361-364.

[10]Siegman A E.New developments in laser resonators[C].SPIE,1990,1224:2-14.

[11]Dan Y,Zhang B.Second moments of partially coherent beams in atmospheric turbulence[J].Opt.Lett,2009,34(5):563-565.

[12]Ji X L,Li X Q.Effective radius of curvature of partially coherent Hermite-Gaussian beams propagation through atmospheric turbulence[J].Opt.,2010,12(3):035403.

[13]LIU Yangyang,Lü Qiunbo,ZHANG Wenxi.Simulation for space target interference imaging system distorted by atmospheric turbulence.Acta Phys.Sin.,2012,61(12):124201.(in Chinese)

劉揚陽,呂群波,張文喜.大氣湍流畸變對空間目標清晰干涉成像仿真研究[J].物理學報,2012,61(12):124201.

[14]Salem M,Korotkova O,Dogariu A,et al.Polarization changes in partially coherent electromagnetic beams propagating through the turbulent atmosphere[J].Waves in Random Media,2004,14(4):513-523.

[15]Zhang E T,Ji X L,Lv B D.Propagation of the off-axis superposition of partially coherent beams through atmospheric turbulence[J].Chin.Phys.B,2009,18(2):571-580.

[16]Casperson W L,Hall D G.Sinusoidal-Gaussian beams in complex optical system[J].J.Opt.Soc.Am.A.,1997,14(12):3341-3348.

[17]YUAN Zhongheng,ZHANG Wentao.The analisis and research for the laser beam through onflow atmosphere channel[J].Laser & Infrared,2006,36(4):272-274.(in Chinese)

袁縱橫,張文濤.大氣湍流對激光信號傳輸影響的分析研究[J].激光與紅外,2006,36(4):272-274.

[18]XIANG Libin,YUAN Yan,Lü Qunbo.Spectral transfer function of the fourier transform spectral imager[J].Acta Phys.Sin.，2009,58(8):5400.(in Chinese)

相里斌,袁艷,呂群波.傅里葉變換光譜成像儀光譜傳遞函數研究[J].物理學報,2009,58(8):5400.

[19]WU Lin,YING Jiaju,GENG Biao.Effect on laser propagation in the atmosphere turbulence[J].Laser & Infrared,2008,38(10):974-977.(in Chinese)

武琳,應家駒,耿彪.大氣湍流對激光傳輸的影響[J].激光與紅外,2008,38(10):974-977.

[20]ZHU Lin,SONG Miao.Numerical simulation of the impact of atmospheric turbulence on the laser signal[J].Laser & Infrared,2013,43(11):1268-1272.(in Chinese)

朱耀麟,宋苗.大氣湍流對激光信號影響的數值模擬[J].激光與紅外,2013,43(11):1268-1272.

Influence of atmospheric turbulence on the Rayleigh range of Gaussian beams

WANG Hui,YANG Jun,ZHANG Xi

(Institute of Science,PLA University of Science and Technology,Nanjing 211101,China)

Rayleigh range;Gaussian beam;atmospheric turbulence;Andrews modified fluctuation spectrum;Von Karman fluctuation spectrum

1001-5078(2015)11-1355-05

總參謀部信息化部通信指揮裝備軍內科研基金(No.KYLYZXJK140002)資助。

王 慧(1981-),男,講師,主研領域為激光傳輸理論。E-mail：wanghuinj@foxmail.com

2015-03-23;

2015-04-09

O436

A

10.3969/j.issn.1001-5078.2015.11.014