基于Bayes-GO 的制動風源子系統可靠性評估

王雯雯 朱愛華 楊建偉

（1.北京建筑大學機電與車輛工程學院 北京 100044 2.北京建筑大學城市軌道交通車輛服役性能保障北京市重點實驗室 北京 100044）

1 引言

近年來，交通安全問題日益突出，隨著人民生活水平的提高，私家車越來越多，軌道交通在緩解城市交通壓力方面起到了重要的作用。然而隨著城市軌道交通建設蓬勃發展，軌道交通安全事故也時有發生，其中事故的發生多與車輛制動裝備有密切關系。因此維護制動系統可靠性，是維護軌道交通安全的重要措施，制動系統是由許多部件及子系統組成的，不同部件和子系統又包含著制動的不同功能，而風源制動系統在制動系統制動中發揮著越來越重要的作用。因此本文特別對風源制動系統部件進行可靠性分析。

由文獻[1]可知，Bayes-GO 方法與復雜系統可靠性評估常用的Monte Carlo 方法相比，運算速度更快，運算精度和運算效率也更高，所以該方法是行之有效的。

2 基于Bayes-go 的風源子系統可靠性評估

2.1 制動風源子系統

風源系統為全列車制動系統、空氣彈簧等裝置提供干燥、清潔的壓縮空氣。風源子系統的結構如圖1 所示，主要包括電動空氣壓縮機、電動空氣壓縮機組的起動裝置、冷卻器、干燥器、濾清器、儲風缸、安全閥、總風壓力開關、壓力調節器、輔助用風裝置、安裝架、彈性安裝件及消音器等部件。從功能上分析，壓力開關控制器用來檢測總風管壓力，控制壓縮機的啟動與關閉。風源壓力控制系統通過壓力控制器檢測壓力值，控制空氣壓縮機的起動與停止，當檢測到的壓力值小于設定值時，正向作用啟動空氣壓縮機大風，反之，反饋作用將空氣壓縮機停止工作，這樣就確保了輸出壓力有一個穩定的閾值。故風源子系統并非為簡單的串聯系統，而是一個閉環可修系統[2]。

圖1 風源子系統的結構Fig.1 Structure of Air Source Subsystem

在風源系統中，空壓機組是關鍵部件。每列車設有兩套電動空壓機組（含過濾、干燥設備以及安全閥等）和兩個總風缸，每輛車配有一個制動輔助風缸，兩種風缸的容積經計算確定。列車配置有順序起動空氣壓縮機的列車線，能夠確保同一列車的兩臺空氣壓縮機在起車前及總風管出現異常泄露時，順序起動。列車的兩套電動空壓機組經列車總風管相連通。在列車正常運行時，兩臺空壓機可分別控制，一臺（列車運行方向前方的空氣壓縮機）正常起動，另一臺備用。

2.2 基于Bayes-GO 的可靠性評估

Bayes 方法可以充分利用單元級的多源先驗信息，而GO 方法又具有直觀、簡便的特點，本文提出的基于 Bayes-go 方法的復雜系統可靠性評估模型，既兼具2 種方法的優點，又克服了上述分析中單一應用一種方法的缺點。

以二級系統為例，Bayes-GO 方法可靠性評估的具體步驟是：首先進行基于Bayes 方法的單元可靠性評估，具體包括單元可靠性先驗信息獲取與處理，單元先驗分布建立和單元驗后分布計算；再完成基于GO 方法的系統可靠性評估，具體包括系統GO模型建立及系統可靠性參數GO 運算[1]。

3 基于Bayes 的風源子系統單元可靠性評估

對各個單元進行可靠性模型的建立，其實就是利用Bayes 方法對各個單元的先驗信息以及抽樣信息分析處理。以空氣壓縮機為例，已知其壽命服從Weibull 分布，對于Weibull 分布，其參數的共扼分布難以找到，但是指數分布的共扼分布是已知的，為伽瑪（Gamma）分布。當威布爾分布的形狀參數m=1 時，威布爾分布即轉化成指數分布。可以看出，指數分布是威布爾分布的一種特殊形式，而當m≠1時可以構造中間量，使它服從指數分布。[1]再由可靠性先驗信息及抽樣信息，求其可靠性參數。

由其壽命服從Weibull 分布W（m，η），其概率密度函數為

式中，η 是尺度參數；m 是形狀參數。

構造中間變量tm，tm服從參數為hm的指數分布，其概率密度函數fE為

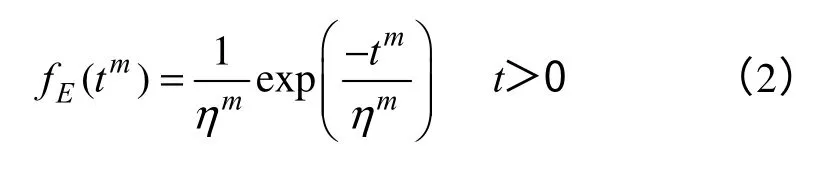
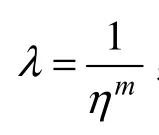
在獲得威布爾分布參數m、η的一些信息后，可以將這些信息轉化為λ的驗前信息。以下是將Weibull 分布轉化成指數分布后的計算過程。

選取λ的先驗分布為共軛驗前Gamma 分布，其密度函數為：

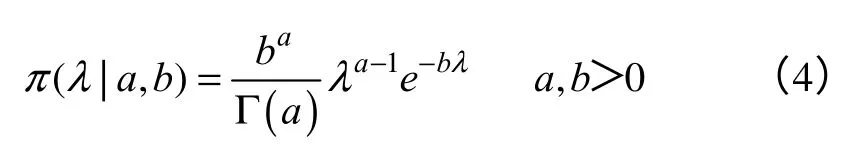
現已知該單元的λ的5%和95%的分位數分別為6.10E-06 和2.07E-05，根據該先驗信息對a、b 進行計算可得到先驗分布中超參數a、b 的值[3]。

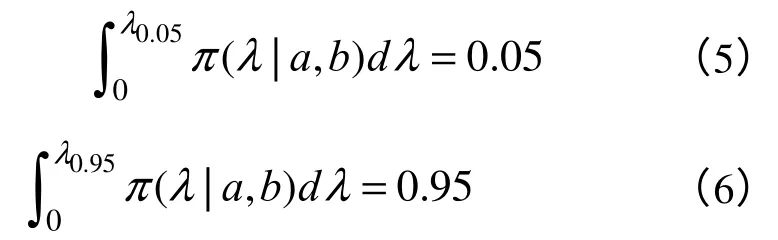
則由計算機可以算出參數a 和b 的值[4]，再結合已有的實驗數據，可得出參數λ的后驗分布的Bayes 估計為

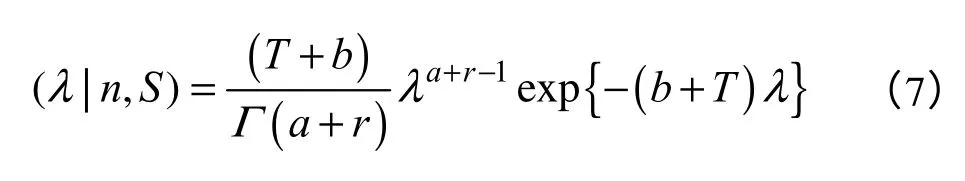
式中，r 為失效次數；T 為試驗總時間。

經計算可得單元二空氣壓縮機的后驗分布服從E（1.21E-5）。由于GO 法運算需要輸入該單元在t時刻成功的概率，根據指數分布的可靠度表達式，空氣壓縮機在t 時刻的可靠度為

采用同樣的步驟，根據已有數據，對其余單元的壽命分布函數可以分別進行運算[1]，得到單元1、單元3～單元10 的壽命分布分別為（3.673E-6）E（1.39E-7）E（4.69E-7）E（9.97E-7）E（4.31E-6）E（5.39E-7））E（4.69E-7）E（5.07E-7）E（1.23E-6）。

以上方法是將對未知先驗分布的Weibull 分布轉化為已知的先驗分布的指數分布的計算過程，根據計算結果對該閉環系統進行GO 運算[4]。

4 基于Go 法的風源子系統可靠性

4.1 風源子系統可靠性GO 模型

根據各個單元連接關系以及工作原理可以看出，電機用操作符5 表示，軟管、安全閥、濾油器、干燥器、止回閥、總風管和壓力開關控制器用操作符1 表示，空氣壓縮機用操作符9 表示[2]。

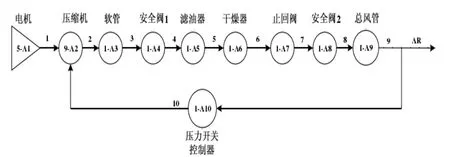
圖2 風源子系統GO 圖Fig.2 Subsystem GO Model

根據上一節運用Bayes 方法，算出空氣壓縮機、電子制動單元、制動控制閥類部件和閘瓦等關鍵部件的可靠性參數，結果見表1。將維修時間對數正態分布近似為指數分布，將平均維修時間的估計值定為維修性指標；其余電子元器件根據元器件的工作環境、工作原理和內部結構，參照國家軍用標準GJB/Z299B—98 選擇可靠性參數；剩余元件或設備的可靠性數據來源于某地鐵列車運營歷史數據統計及經驗值[4]。

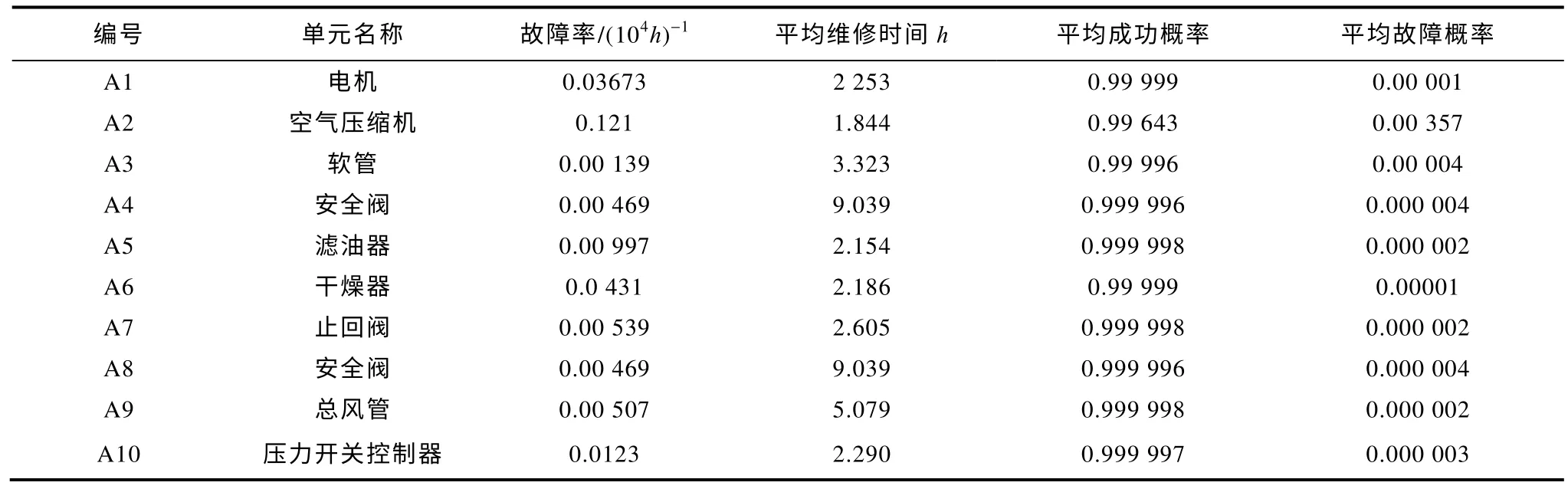
表1 單元可靠性參數Tab.1 Analysis Unit Reliability Parameter

4.2 可靠性參數GO 運算

可修系統是處于正常工作狀態和停工維修狀態交替之中的系統，系統發生故障和完成維修都有隨機性。本文假定動車組風源系統中元件和子系統服從指數分布以及可以轉化為指數分布的分布，則系統的可靠性特征量如下[5]-[9]。

平均無故障工作時間的計算公式為。

式中，λ為故障率平均維修時間的計算公式為

式中，μ為維修率平均壽命周期MCT 的計算公式為

穩態可用度A（平均工作概率）的計算公式為

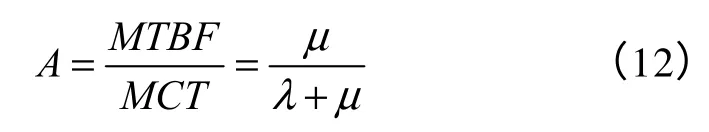
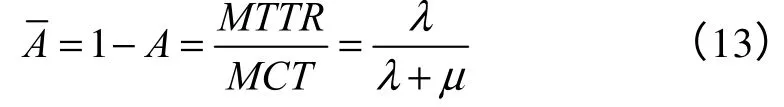
單位時間平均故障次數f 的計算公式為

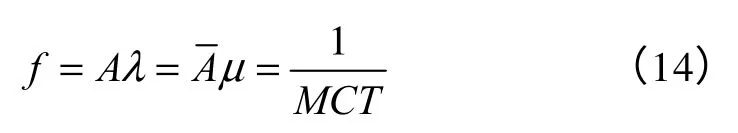
4.3 系統GO 法模型邏輯簡化以及定量分析

可修系統的操作符代表的單元是可修系統，只有成功狀態和故障狀態。穩態時，操作符成功狀態的概率就是單元的可用度，操作符故障狀態的概率就是單元的不可用度，操作符的故障率和維修率就是可修單元的故障率和維修率。GO 法分析過程中信號流代表該信號流前的部分可修系統，只有成功狀態和故障狀態。穩態時，信號流成功狀態概率和故障狀態概率就是其所代表的部分可修系統的可用度和不可用度，信號流所代表的部分可修系統的故障率和維修率稱為信號流的等效故障率和等效維修率。信號流的成功狀態概率，等效故障率和等效維修率不是獨立的，由式（12）聯系，因此以下僅給出其中任意2 個量的計算公式，由式（9～14）可求得所有的可靠性特征量。

由于該子系統為閉環可修制動系統，所以運用閉環可修系統的GO 法來化簡該系統。可得到該系統簡化GO 圖如圖3 所示[6]。A3～A9 屬于串聯邏輯結構，考慮停工相關，做一個等效處理單元M，如圖3a 所示。然后將M 與A10 等效為單元AM，如圖3b 所示[2]。后將M 與A2 等效為E 單元，如圖3c 所示。

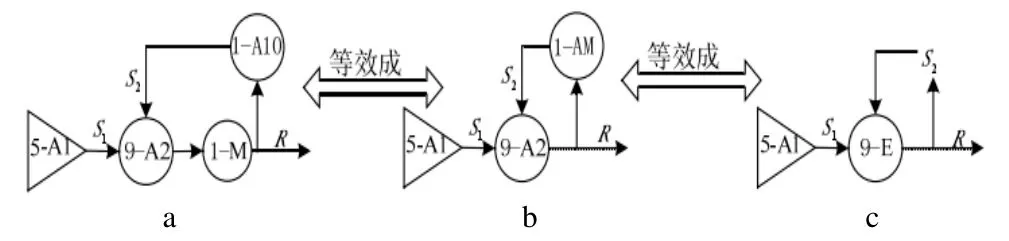
圖3 系統簡化GO 圖Fig.3 Simplified GO figure of system

其中，根據go 法操作符中的與門計算公式可以得到簡化后λAM以及μAM計算公式為

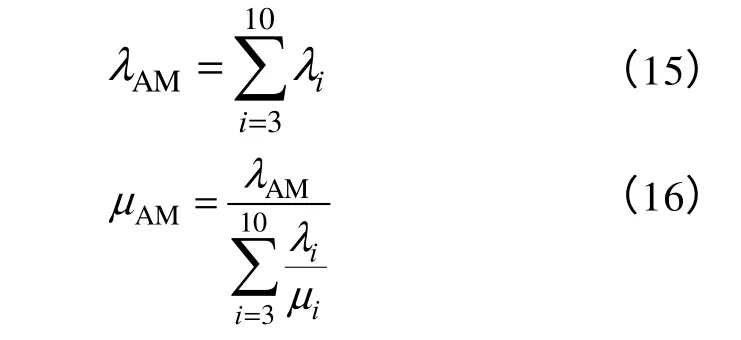
進而可以求出的λE以及μE為

最終可以得到該閉環系統可靠性參數穩態值為

根據以上GO 運算法則[7-9]，得到風源子系統可靠性數據，見表2

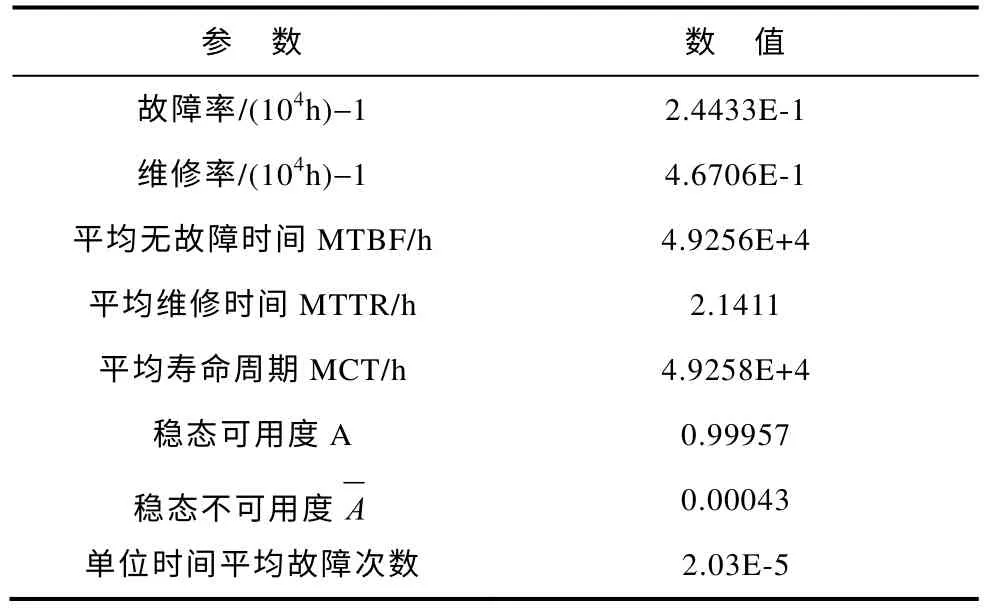
表2 可靠性分析結果Tab.2 Results of Reliability Analysis

4.4 計算結果對比

計算結果均由計算機Matlab 編程所得，結果表明，該方法算出的平均無故障時間為49 256 h，明顯比文獻[10]中沒有結合先驗信息單獨由GO 法所得的平均維修時間所得的平均無故障時間要長，證明該方法不僅運算效率高，精度好，而且經過技術的不斷改進，風源系統的可靠性有大幅度的提高，更能保障列車的正常運營。

5 結論

本文針對軌道車輛制動系統中風源子系統的可靠性評估，首先利用先驗信息和采樣信息運用Bayes 方法獲得單元可靠性的后驗參數，再根據所得的后驗參數利用GO 法進行定量分析和計算，最終得到系統的可靠性參數。這樣就巧妙的將Bayes和GO 法結合起來。Bayes 方法的使用，可以有效地利用經驗信息，使估計結果最大限度地客觀真實。GO 法的使用，使整個系統可靠性運算更加簡單快捷，在復雜系統中其優勢更為明顯。雖然僅僅分析了一個簡單的串聯閉環可修系統，但是可以將其原理及思路推廣至整個制動系統以及其他復雜可修系統，充分體現Bayes 和GO 的優點以及盡可能避免單獨使用其中一種方法的缺點。

[1]尹宗潤,李俊山,蘇東,孫衍欣.基于Bayes-GO 的復雜系統可靠性評估模型[J].計算機工程,2013,39(11):226-230.Yin Zongrun,Li Junshan,Su Dong,Sun Yanxin.Reliability Assessment Model of Complex System Based on Bayes-GO[J].Computer Engineering,2013,39(11):226-230.

[2]董軍哲.城市軌道交通車輛制動系統可靠性建模及仿真研究[D].山西:太原科技大學,2009.Dong Junzhe.Urban Rail Transit Vehicle Brake System Reliability Modeling and Simulation Research,[D].Shan xi:Taiyuan University of Science and Technology,2009.

[3]范英,田志成.基于Bayes 方法的小子樣可靠性分析[J].機械強度,2012,34(2):274-277.Fan Ying,Tian Zhicheng.Reliability Analysis on Small Sample Based on Bayes[J].Journal of Mechanical Strength,2012,34(2):274-277.

[4]彭照光,李傳日.基于Bayes 的指數分布型無故障驗證試驗方案[J].現代預防技術,2010,38(2):25-27.Peng Zhaoguang,Li Chuanri.Failure-Free Compliance Test Plan of Exponential Distribution Based on BayesTheory[J].Modern Defence Technology,2010,38(2):25-27.

[5]沈祖培,黃祥瑞.GO 法原理及應用[M].北京:清華大學出版社,2004.Shen Zupei,Huang Ruixiang.The Principle and Application of the GO Methodology,Beijing:Tsinghua University Press,2004.

[6]黃軼州,石全,郝晉峰,溫亮.基于GO 法的制動系統可靠性分析[J].自動測量與控制,2008,27(11):77-78.Huang Yizhou,Shi Quan,Hao Jinfeng,Wen Liang.Automobile Brake System Reliability Analysis Based on GO Method[J].Automatic Measurement and Control,2008,27(11):77-78.

[7]董軍哲,楊建偉,黃強.基于 GO 法地鐵車輛客室車門可靠性評價[J].城市軌道交通研究,2013,19(4):28-32.Dong Junzhe,Yang Jianwei,Huang Qiang.Reliability Analysis of Passenger Compartment Door of Metro Vehicles Based on GO Method[J].Urban rail transportation research Investigate,2013,19(4):28-32.

[8]蔡國強,周莉茗,李熙,等.基于GO 法的城市軌道交通車門系統可靠性分析[J].西南交通大學學報,2011,46(2):264-230.Cai Guoqiang,Zhou Liming,Li xi.Reliability Analysis of Urban Rail Transit Vehicles Door System sBased on GO Method[J].Journal of Southwest Jiaotong University,2011,46(2):264-230.

[9]陳民武.基于GO 法的高速鐵路牽引變電所可靠性評估[J].電力系統保護與控制,2011,39(18):58-60.Chen Minwu.The reliability assessment of traction substation of high speed railway by the GO methodology[J].Power System Protection and Control,2011,39(18):58-60.

[10]張敏娜,楊建偉,黃強.基于 GO 法動車組風源系統可靠性分析[J].鐵道車輛,2014,52(3):31-33.Zhang Minna,Yang Jianwei,Huang Qiang.The EMP Pouring System Reliability Analysis Based On GO methodology.Railway vehicles,2014,52(3):31-33.