混合鄰域結構的粒子群算法

張澤星

（石家莊經濟學院網絡信息安全實驗室，河北石家莊 050031）

粒 子 群 算 法（particle swarm optimization，PSO）是KENNEDY 和EBERHART 兩位博士于1995年提出的新型進化算法［1］，因其具有易于實現、精度高、收斂快等優點，且在解決實際問題中表現優異，自提出以來便受到了學術界的廣泛重視［2－3］。然而，標準PSO 算 法 的 缺 點 也 是 明 顯 的［4］，首先容易出現陷入局部極值、早熟收斂或停滯現象。其次，PSO 的性能也依賴于算法參數。為此，研究人員分別采用粒子群初始化、鄰域拓撲、參數選擇和混合策略等改進措施克服上述不足［4］。

為避免由于粒子向自身歷史最佳位置和群體歷史最佳位置聚集，形成粒子種群的快速趨同效應現象，在分析不同拓撲結構對算法性能影響的基礎上，結合全局模型，同時使用無標度網絡作為局部鄰域拓撲，在標準測試函數上的實驗結果表明，該方法可有效平衡算法的開采和挖掘能力，性能良好。

1 全局模型與局部模型

1.1 標準粒子群算法（SPSO）

基本粒子群算法的數學表示如下：設搜索空間為D維，由n個粒子組成種群；用Xti和Vti分別表示第i個粒子在第t步迭代時所處的位置和飛行速度：Xti＝（xti1，xti2，…，xtiD），Vti＝（vti1，vti2，…，vtiD）；記pti和ptg分別為到第t次迭代為止，第i個粒子自身經歷的最佳位置和種群經歷的最佳位置。

每個粒子的位置按如下公式變化：

式中：w為慣性因子；d＝1，2，…，D；i＝1，2，…，n；t為當前迭代次數；c1，c2為正的常數，稱為加速因子；r1和r2為［0，1］區間內的均勻隨機數。

式（1）將其他全部粒子視為當前粒子的鄰域，pgd是該鄰域中粒子的歷史最佳位置，該模型被稱為全局模型。除了全局模型外，EBERHART［5］等最早提出了局部版的粒子群算法。局部模型將式（1）中的pgd替換為pld，pld代表當前粒子的拓撲鄰域中所有粒子的最優位置。目前，已被廣泛接受的結論是：鄰域結構是決定PSO 算法效果的極重要因素，這是因為鄰域結構決定了優秀等位基因的傳播和混合，從而影響到搜索性能［6］。前人的研究表明［7］，全局模型收斂速度較快，具有較強的局部搜索能力，但魯棒性較差；局部模型收斂速度較慢，但具有較強的全局搜索能力，魯棒性較好。本文將這2種模型結合在一起，設計了一種新的混合模型。

1.2 鄰域拓撲分析

式（1）被稱為全局模型，該模型中，粒子i的鄰域集合為P－｛i｝，其中，P為全體粒子。也就是說，任何2個粒子之間均存在著“聯系”，從而，全局模型的鄰域拓撲為一個完全圖。

局部模型的鄰域拓撲主要有［7－8］1）環形拓撲：所有粒子首尾互連構成一個環。2）星形拓撲：以其中一個粒子為中心，該中心與相鄰的其他粒子進行信息交換，且其他粒子之間互不聯系。3）塔形拓撲：也稱K面體結構，粒子分布在K面體的K個頂點上，然后所有K面體再相互連接起來。4）馮·諾依曼拓撲：用三維網格的形式把粒子與它上下左右4個最鄰近的粒子相互連接，形成立體網狀結構。

上述提到的拓撲結構特點主要有2個：靜態性和規則性，即拓撲結構是事先給定的規則圖。考慮到個體交互的隨機性，研究人員將動態變化或非規則的拓撲結構引入局部模型，做法分為3類：第1類是從空間距離的角度劃分鄰域。早在1999年，SUGANTHAN［9］引入一個時變的歐氏空間鄰域算子：在搜索初始階段，將鄰域定義為每個粒子自身；隨著迭代次數的增加，將鄰域范圍逐漸擴展到整個種群。再如：范成禮［10］等提出了帶審斂因子的變鄰域粒子群算法，有效避免了常規PSO 算法在復雜多峰函數的求解過程中容易陷入早熟收斂的問題，提高了全局搜索能力。第2類單純從粒子的社會關系角度進行鄰域動態或非規則劃分，如：彭虎［11］等將隨機拓撲和馮·諾依曼拓撲相結合形成動態社會關系鄰域；GONGSUN［12］等將基于小世界網絡的鄰域結構引入到粒子群優化求解中。還有一類借助子群或簇來建立信息交換的拓撲結構，如：郭文忠［13］等基于“簇”思想，對粒子間距離進行重新定義并給出了相應的動態鄰域PSO 算法。再如：倪慶劍［14］等引入了一種粒子群信息共享方式——多簇結構，進而提出了動態可變拓撲策略以協調動態概率粒子群優化算法的勘探和開采能力。針對不同的優化問題，這些拓撲的性能表現各異；但總的來說，隨機拓撲往往對大多數問題能表現出較好的性能［4］。

2 混合拓撲模型

2.1 使用混合拓撲的PSO

使用復雜網絡作為局部鄰域首先要解決的問題是建立復雜網絡。建立復雜網絡的算法有許多，本文采用無標度網絡作為鄰域拓撲，建立該類型網絡的最知名的算法莫過于BA 網絡模型。BA 模型具體描述如下［15］。

假設網絡最初有m0個節點。每一次加入一個新節點，每次加入的新節點通過m（m≤m0）條新加入的連接邊與網絡中已有的m個節點相連。每個新節點與節點i相連的概率∏（ki）依賴于節點i的度ki，且該概率服從如下規則：

重復加入t個節點后，將得到一個有N＝t＋m0個節點和mt條邊的網絡。

其次，需要建立粒子與網絡節點之間的映射，映射的方法有2種：1）當節點數與粒子數相等時，可以采用一對一的映射；2）當節點數大于粒子數時，可以采用多對一的映射，即一個粒子對應網絡上多個節點。本文采用的是第2種方式。不妨設映射函數為f：i→N（i），它將粒子i映射到網絡節點集N（i）上，N（i）＝｛N1（i），N2（i），…，N｜N（i）｜（i）｝；其中，網絡節點Nj（i）（j＝1，2，…，｜N（i）｜）的鄰居集合為｛Nj1（i），Nj2（i），…，N｜Nj（i）｜（i）｝。在迭代時，按如下步驟確定粒子i的鄰域。

步驟1：借助映射函數，確定i對應的網絡節點集合N（i）；

步驟2：隨機從N（i）中取一個元素，不妨設為Nj（i）；

步驟3：將Nj（i）的鄰居作為i的鄰域。

基于無標度網絡鄰域結構的粒子群算法的主體流程如下。

步驟1：初始化運行參數；

步驟2：初始化速度和位置；

步驟3：計算適應度；

步驟4：創建無標度網絡；

步驟5：建立粒子與網絡節點的映射關系；

步驟6：WHILE（滿足迭代條件）；

6.1 如果最優解沒有更新；

6.1.1 為每個粒子產生鄰域；

6.2 對每個粒子；

6.2.1 從其鄰域中找到最優個體；

6.2.2 更新速度與位置；

6.3 更新個體最優歷史；

6.4 更新種群最優歷史；

步驟7：返回最優個體。

上述算法中，速度更新公式如下：

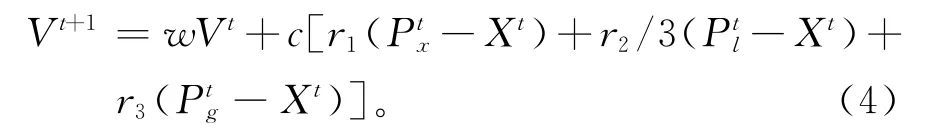
式中：Px，Pl，Pg分別代表粒子的歷史最優、鄰域最優及種群最優；w，c分別為慣性因子和加速因子；r1，r2，r3分別為［0，1］內的3個隨機數。

位置更新公式如下：

2.2 算法分析

全局模型的拓撲是一個完全圖（規則圖）；大量研究結果表明：使用隨機拓撲的粒子群算法效果良好。然而，現實中的網絡即非規則圖也非隨機圖，大多數現實網絡都呈現無標度特性。因此，使用無標度網絡作為鄰域拓撲使粒子的交互結構更貼近現實。從式（4）來看，速度更新考慮了粒子自身的歷史、鄰域和種群三方面信息，從另外一個角度來說，本文設計的是介于全局和局部模型之間的混合模型。

從上面的描述來看，粒子的鄰域是動態變化的，粒子i映射的網絡節點集為N（i）＝｛N1（i），N2（i），…，N｜N（i）｜（i）｝，粒子的鄰域取決于：1）從N（i）中隨機抽取的是哪個網絡節點；2）隨機抽取的網絡節點（不妨設為Nj（i））的度及其相鄰節點。

由于無標度網絡符合冪律分布，設在網絡中隨機抽取到度為k的節點概率為p（k），可以證明［15］：

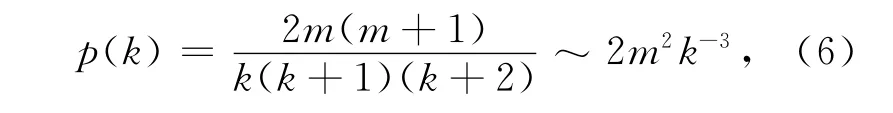
該式說明，度越大的節點出現在網絡中的概率越小。也就是說，大多數粒子的鄰域規模都比較小。

在空間和時間復雜度方面，與標準粒子群算法相比，本文算法空間上需要額外存儲復雜網絡；時間上增加了尋找粒子鄰域的支出。收斂性方面，由于并未從根本上改變粒子群算法的流程，因此，本文算法的收斂性證明與標準粒子群算法一致。

3 實驗結果

借助實驗，需要探究的問題包括：1）算法的性能比較；2）算法的收斂情況；3）不同維度與不同運行參數下的算法性能；4）復雜網絡節點數與算法性能的關系；5）運行時間的比較分析等等。由于篇幅關系，本文僅針對于問題1）和問題2）進行詳細的實驗及其結果分析。

3.1 實驗設計

實驗采用的3個經典測試函數分別描述如下。

這3個函數各有特點，如圖1所示，f1有明顯的全局最優，梯度變化明顯；f2在相對“平坦”的區域有許多局部最優；f3的梯度變化不明顯。相比之下，f1的全局最優最容易尋找；f2和f3尋全局最優解則都比較困難，分別要求算法具有較強的逃逸局部最優的能力（也可以說是勘探能力）和持續進化的能力（或說是開采能力）。

比較算法來自于SPSO2011［16］，其源代碼從文獻［17］獲取。每個測試函數上獨立運行10次，分別記錄：在所有運行中找到最好解（記為HB）、每次獨立運行最優解的平均值和方差（分別記為MEAN和STD）。從某種程度上講，HB越好則算法的開采能力越強。平均數反應的是數據的集中趨勢，越集中說明算法性能越穩定；方差反映的是離散程度，從某種意義上講，越離散說明算法魯棒性越差。

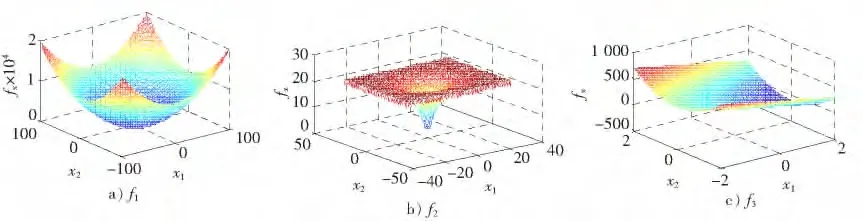
圖1 測試函數圖形Fig.1 Figure of test functions

3.2 實驗結果及分析

實驗一：性能比較。函數維度D＝20，網絡節點數取為100，粒子個數為30。公平起見，其他參數設置同所比較的SPSO2011 代碼［17］。實驗結果見表1，方便起見，以下將本文算法簡記為NPSO。表1中，指標值更好的結果用黑體表示。不難看出，本文算法全面超過了SPSO。

表1 性能比較結果Tab.1 Compared results of performance

從表1來看，在f1上，NSPO 取得的STD 非常小且其MEAN 接近HB，說明NPSO 總能為f1找到非常優異的解。這得益于f1僅有一個全局最優，而且梯度變化明顯（見圖1）。但盡管如此，SPSO 僅能找到7.752 574e－05這樣的解，遠次于NPSO 的7.230 542e－133。這可能是因為在f1的“底部”，地勢較平坦，盡管全局不存在局部最優，但SPSO 在較平坦的底部地形上，“前進”非常困難，而NPSO針對于這樣的地形，尋優能力優越。

在f2上，NSPO 的HB指標值遠優于SPSO，但兩者均值相差不大。實驗中發現，NSPO 在f2上，多數情況下能找到10－15這一數量級的解，偶爾找到100這一數量級的差解。對應的，SPSO 最好解的數量級在10－5，最差解的數量級為100。這反應出NSPO 跳出局部最優解的能力要強于SPSO。但由于f2存在大量的局部最優，盡管NSPO 的勘探能力強于SPSO，但仍有很大提升空間。

在f3上，NSPO 的STD 大于SPSO，但HB 小于SPSO，說明NSPO 具備找到更好解的能力。由于f3的梯度信息不明顯甚至存在“誤導”的梯度信號，比如：從當前位置向左尋找確實能使得解得以進化，但如果正確的方向應該是向下，則“向左”的梯度可能會誤導算法走向錯誤的方向。如此，則會大大降低算法的搜索效率。正因為此，最好情況下，NSPO只找到了10－4這一數量級的解。

實驗二：收斂性實驗。收斂性結果可以從某種程度上反應出算法是否早熟；從某種程度上揭示參數對收斂性及性能的影響等。圖2給出了NPSO與SPSO 一次獨立運行中收斂結果的比較示意圖，本實驗采用的運行參數完全同于實驗一。圖2a），c），e）分別是NSPO 在f1，f2，f3上的收斂示意圖；圖2b），d），f）分別是SPSO 在3個測試函數上的收斂示意圖。

圖2b）明顯反應出SPSO 在f1上存在早熟或停滯現象，最優解僅僅進化了100余次。從圖2a）看出，NSPO 在f1上進化了近2 000次。

在f2上，要求算法必須不斷地逃逸出局部最優。圖2c）和圖2d）顯示，NSPO 的進化次數是SPSO 的3倍多。這說明NSPO 的逃逸能力要強于SPSO，但終究還是在進化了500余次后陷入了無法逃出的某個局部解。這種情況下，增加迭代次數對提高算法性能顯然是無益地。

圖2 收斂對比結果Fig.2 Compared results of convergence

在f3上，不存在局部最優解，但存在大量的“誤導”梯度。從圖2d）和圖2f）可以看出，2種算法均進化了3 000 余次，在一定的迭代次數內，無論是NSPO 還是SPSO，算法總能進化，但這種持續的進化最終使得2種算法均出現“南轅北轍”的現象。但總體上，NSPO 克服“誤導”梯度的能力要更強一些。

4 結 語

本文提出的算法綜合了全局和局部模型，粒子的局部鄰域拓撲根據無標度網絡的結構確定。實驗結果表明，借助無標度網絡作為鄰域拓撲是可行的。與標準PSO 的全局模型相比，本文算法在避免早熟、陷入局部最優、停滯這些缺點上，有較好的改善。新算法的適應性、魯棒性更強，具有較強的可應用性和拓展性。

／References：

［1］ KENNEDY J，EBERHART R C.Particle swarm optimization［A］.Proceedings of IEEE International Conference on Neural Networks［C］.Piscataway：IEEE Press，1995：1942－1948.

［2］ RADA－VILELA J，JOHNSTON M，ZHANG M J.Deception，blindness and disorientation in particle swarm optimization applied to noisy problems［J］.Swarm Intelligence，2014，8（4）：247－273.

［3］ SHEN M，ZHAN Z H，CHEN W N，et al.Bi－velocity discrete particle swarm optimization and its application to multicast routing problem in communication networks［J］.IEEE Transactions on Industrial Electronics，2014，61（12）：7141－7151.

［4］ 戴 朝 華.粒 子 群 優 化 算 法 綜 述［EB／OL］.http：／／www.doc88.com／p－30490875816.html，2010－05－24.DAI Zhaohua.A Suvery of Particle Wwarm Optimization［EB／OL］.http：／／www.doc88.com／p－30490875816.html，2010－05－24.

［5］ EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory［A］.Proceedings of the 6th International Symposium on Micro Machine and Human Science［C］.［S.l.］：IEEE Xplore，1995：39－43.

［6］ PAYNE J L，GIACOBINI M，MOORE J H.Complex and dynamic population structures：Synthesis，open questions，and future directions［J］.Soft Computing，2013，17（7）：1109－1120.

［7］ KENNEDY J.Small worlds and mega－minds：Effects of neighborhood topology on particle swarm performance［A］.Proceedings of the IEEE Congress on Evolutionary Computation［C］.Washington：IEEE，1999：1931－1938.

［8］ KENNEDY J，MENDES R.Population structure and particle swarm performance［A］.Proceedings of IEEE Congress on Evolutionary Computation［C］.Honolulu：［s.n.］，2002：1671－1676.

［9］ SUGANTHAN P N.Particle swarm optimiser with neighbourhood operator［A］.Proceedings of the IEEE Congress on Evolutionary Computation［C］.Piscataway： NJ，1999：1958－1962.

［10］ 范成禮，邢清華，范海雄，等.帶審斂因子的變鄰域粒子群算法［J］.控制與決策，2014，29（4）：696－700.FAN Chengli，XING Qinghua，FAN Haixiong，et al.Particle swarm optimization and variable neighborhood search algorithm ith convergence criterions［J］.Control and Decision，2014，29（4）：696－700.

［11］ 彭虎，張海，鄧長壽.動態鄰域混合粒子群優化算法［J］.計算機工程，2011，37（14）：211－213.PENG Hu，ZHANG Hai，DENG Changshou.Dynamic neighborhood hybrid particle swarm optimization algorithm［J］.Computer Engineering，2011，37（14）：211－213.

［12］ GONGSUN Y J，ZHANG J.Small－world particle swarm optimization with topology adaptation［A］.Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation［C］.［S.l.］：［s.n.］，2013：25－32.

［13］ 郭文忠，陳國龍，洪玉玲.求解TSP問題的動態鄰域粒子群優化算法［J］.漳州師范學院學報，2007，20（2）：37－41.GUO Wenzhong，CHEN Guolong，HONG Yuling.Dynamic neighborhoodd particle swarm optimization for TSP［J］.Journal of Zhangzhou Normal University，2007，20（2）：37－41.

［14］ 倪慶劍，張志政，王蓁蓁，等.一種基于可變多簇結構的動態概率粒子群優化算法［J］.軟件學報，2009，20（2）：339－349.NI Qingjian，ZHANG Zhizheng，WANG Zhenzhen，et al.Dynamic probabilistic particle swarm optimization based on varying multi－cluster structure［J］.Journal of Software，2009，20（2）：339－349.

［15］ BARABASI A L，ALBERT R.Emergence of scaling in random networks［J］.Science，1999，286：509－512.

［16］ CLERC M.Standard Particle Swarm Optimisation：From 2006 to 2011［EB／OL］.https：／／hal.archives－ouvertes.fr／hal－00764996，2012－09－23.

［17］ OMRAN M G H.Standard PSO Source Code Version 2011［EB／OL］.http：／／www.particleswarm.info／standard＿pso＿2011＿c.zip，2011－11－04.