基于混合邏輯動態模型的逆變器和電機建模仿真
羅 凱,崔博文
(集美大學,福建廈門 361021)
基于混合邏輯動態模型的逆變器和電機建模仿真
羅 凱,崔博文
(集美大學,福建廈門 361021)
逆變電路是一個由離散的控制信號驅動連續狀態變量隨時間演化的典型的混雜系統,傳統的基于數學模型的建模方法要么只考慮了系統的離散控制變遷忽略了系統的連續狀態變遷,要么只考慮系統的連續狀態變遷忽略了系統的離散控制變遷,這非常容易造成重要故障信息的丟失,大大影響故障診斷的實時性和可靠性。通過分析逆變器和電機系統的運行模式,建立逆變器和電機的混合邏輯動態模型,并運用MATLAB/SIMULINK對逆變器和電機的故障模式進行仿真分析,仿真結果表明該方法很好地描述了逆變器故障時系統的輸出特性,為后續的故障診斷提供準確的故障信息。
逆變電路;混合邏輯動態模型;故障模式;仿真
0 引言
在電機驅動系統中,逆變器根據控制器發出的開關信號調制出一定頻率和幅值的電壓脈沖序列,是一個典型的非線性環節,這些電壓脈沖作用在感性的電機繞組上產生連續的狀態電流,因此,逆變器和電機構成了一個由離散事件驅動連續狀態演化的混雜系統。而現有的基于逆變器數學模型的建模方法中多采用狀態空間平均法,對一個調制周期內的開關模式做時域上的平均處理,無法將瞬態過程揭示出來,例如逆變器傳統開關函數模型,只考慮了電路控制變遷,而沒有描述與電路連續狀態相關的條件變遷,這可能導致重要故障信息的丟失,不能用于功率管故障狀態時的分析。而混雜系統(Hybrid System,HS)是指離散事件系統和連續變量系統相互混雜、相互作用而形成的統一動態系統,不僅可以描述電感電流連續時的電路特性,又可以描述電感電流斷續時的電路特性。因此使用混雜系統對逆變器和電機系統建模可以獲得更為準確的數學模型,更好地實現系統的分析和診斷。
1 逆變器和電機的混雜系統建模及故障分析
1.1 電機驅動系統的運行模式分析
電機及其驅動系統一般由電機本體、功率變換器、轉子位置傳感器和控制器四部分構成[1]。功率變換器是AC-DC-AC環節,其中的AC-DC是整流環節,DC環節使用了濾波電容以提升直流輸出質量,DC-AC環節是逆變環節,電機三相繞組采用星型連接。當系統正常運行時,控制器接收指令和反饋的三相電流信息和電機位置角信息,然后將反聵信息轉變成開關信號S1~S6輸出,開關信號經過系統的隔離與驅動輸入到DC-AC環節中,DC-AC環節能夠產生離散電壓脈沖信號,這些離散的電壓脈沖信號輸入到帶有電感的電機中產生連續的狀態電流。圖1是逆變器和電機的等效電路。
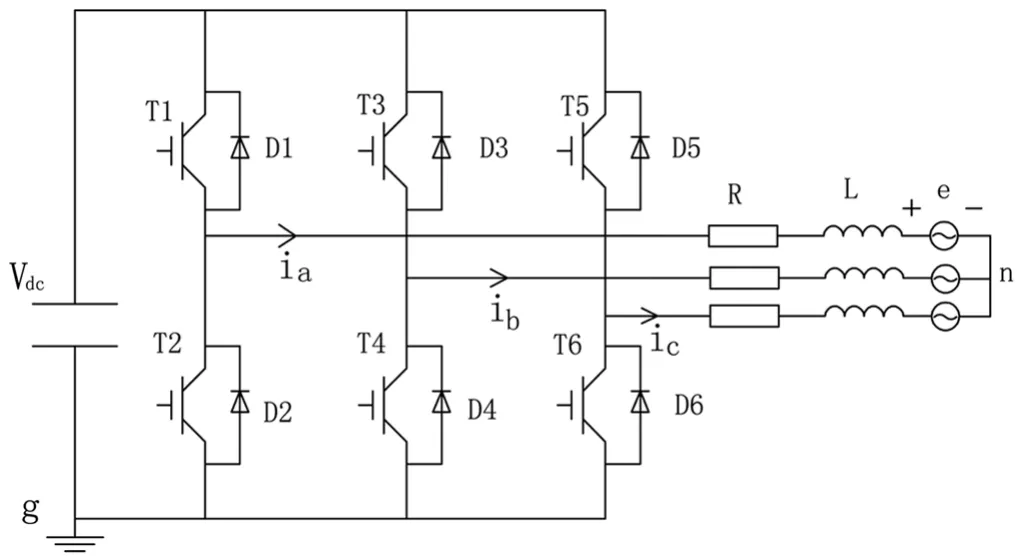
圖1 逆變器和電機系統等效電路
1.2 逆變器和電機的混雜系統模型
對圖1中的逆變器和電機等效電路,根據基爾霍夫定律求得電機的三相繞組電壓表達式為:
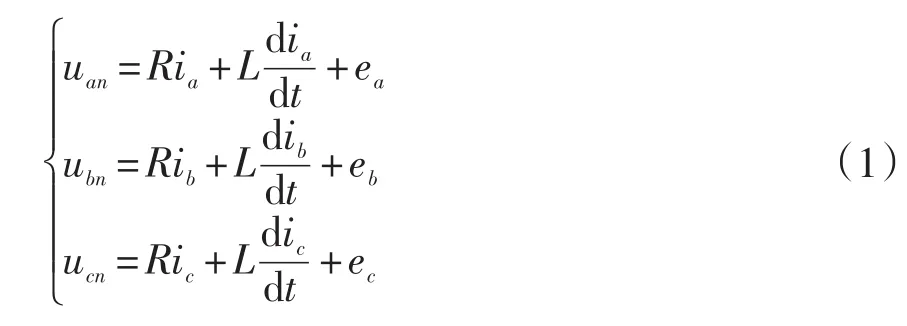
其中,uan、ubn、ucn為電機繞組和電路假想中點n之間的三相電壓(V);
ia、ib、ic為電機三相繞組電流(A);
ea、eb、ec為電機三相反電勢(V);
R為電機三相繞組電阻(Ω);
L為電機定子電感(H),L=LS-M,其中 LS為自感,M為互感。
假設T1~T6都為理想開關,并規定電路中電流流入電機三相繞組為正,電流流出為負,用S1=0表示T1斷開,S1=1表示T1導通,依次類推S6=0表示T6斷開,S6=1表示T6導通。以電路中a相繞組為例,設在a點和g點之間的電壓為uag,那么有:

對于采用三相對稱星型繞組,有ia+ib+ic=0,又由于電機的三相反電勢是處于平衡狀態的,即有ea+eb+ec=0,結合式(1)得:

進而求解出電機三相電壓方程是:
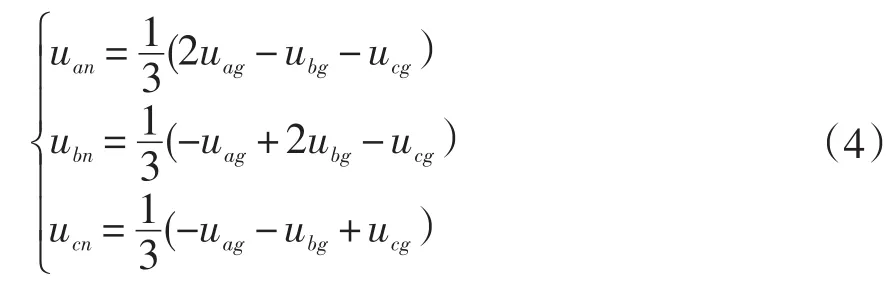
定義輔助邏輯變量δa、δb、δc令:
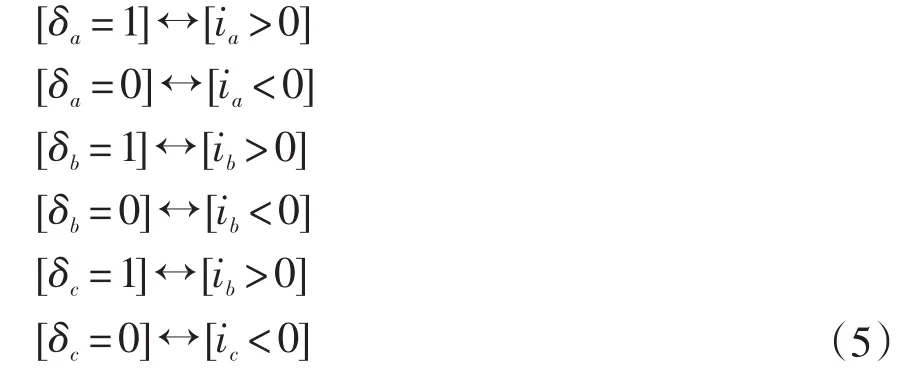
結合式(4)有下列邏輯關系:
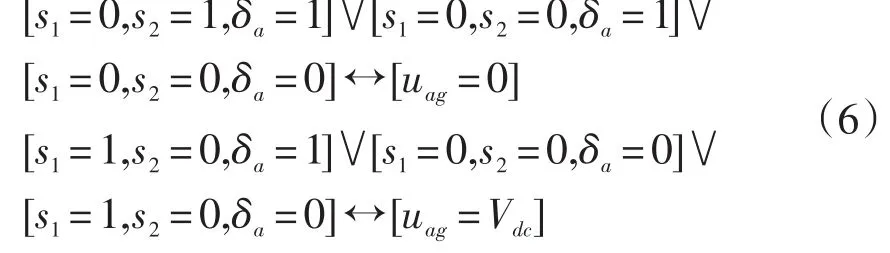
同理可得電機驅動系統電壓的混合邏輯動態模型為:
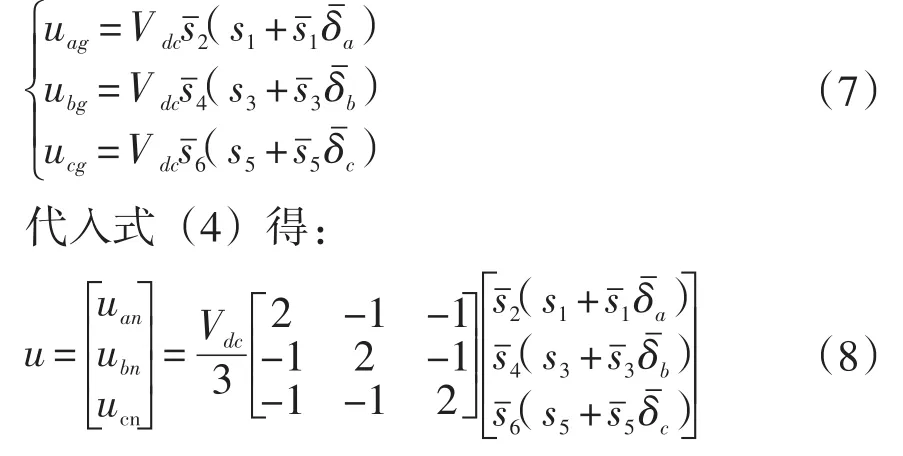
同理代入式(1)可得:
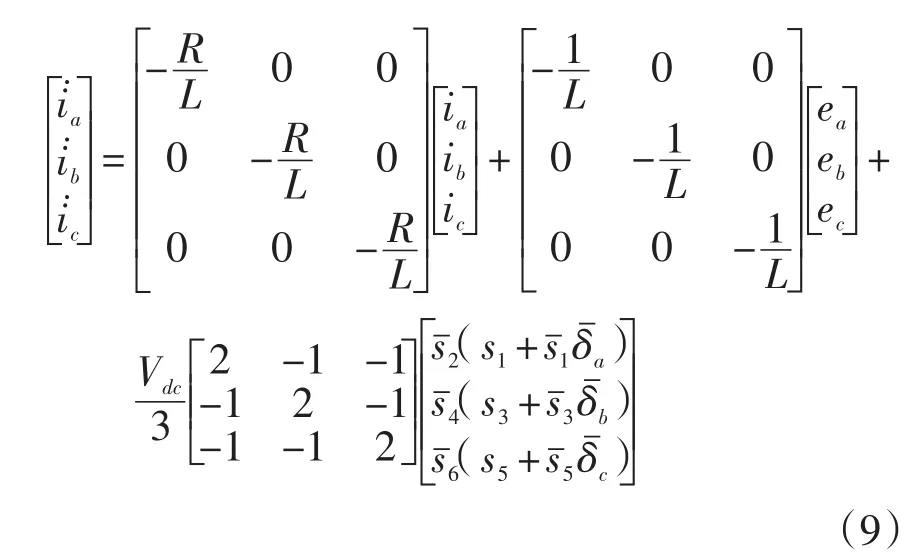
設δ=[δ1δ2δ3]T,令:

可得以電流為狀態變量的電機驅動系統混合邏輯動態模型為
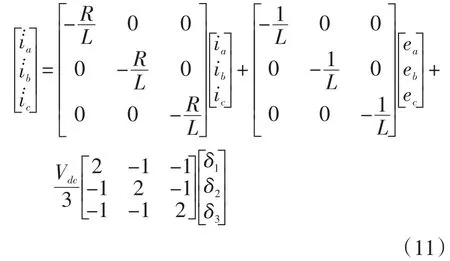
用向量表示為

利用式(12)構建電機驅動系統的健康混合邏輯動態模型狀態估計器:

用式(12)減去式(13)可得系統狀態殘差為

1.3 逆變器故障模式分析
逆變器故障主要發生在逆變電路的功率開關元件上,且是電機驅動系統發生故障的主要原因,在電機驅動系統中,逆變電路主電路常見的故障模式[2]有:
(1)任一功率開關元件發生短路故障;
(2)任一功率開關元件發生開路故障;
(3)同一相橋臂兩功率開關元件同時發生開路故障。
通常情況下可以采用功率開關元件與熔斷器進行串聯的方式[3],當功率開關元件發生短路故障時熔斷器斷開,因此可以將短路故障可以等同于開路故障來研究。
以逆變器a相為例,當T1發生開路故障時有S1=0,則有:

當T2發生故障是有S2=0,則有:

當T1和T2同時發生故障時,則有:
當T1發生故障時,則有:

設故障前殘差初始值為零,寫出方程組形式有:
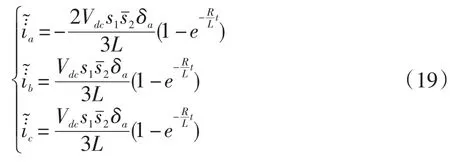
當T2發生故障時有:
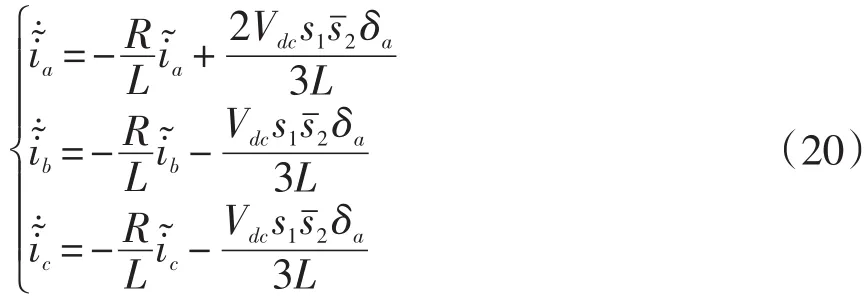
當T1和T2同時發生故障時有:
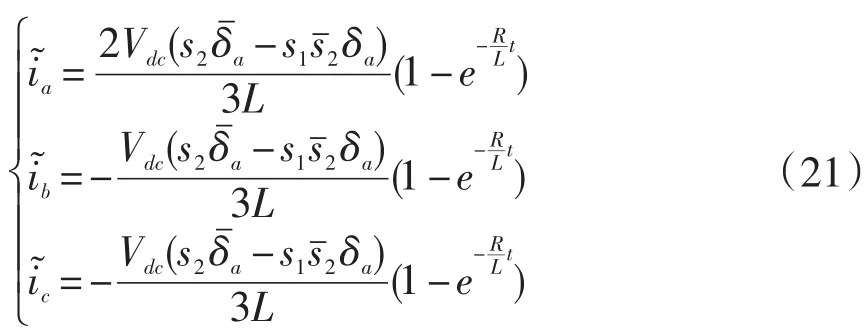
2 仿真和結果分析
在MATLAB/SIMULINK仿真環境下搭建永磁同步電機系統及其MLD模型,其中濾波電感、電阻、電容分別為:100 μH、20 mΩ、0.01 F,母線電壓320 V,開關頻率10 kHz,給定轉速2 400 r/min,負載轉矩2 N·m,假設當t=0.1 s時,a相橋臂上管T1開路故障、下管T2開路故障及T1與T2同時開路故障的仿真結果分別如圖2~10所示。
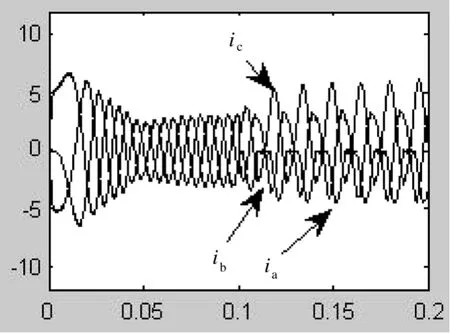
圖2 T1在t=0.1 s故障時實際三相電流
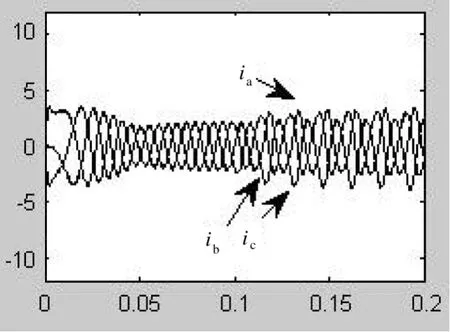
圖3 T1在t=0.1 s故障時MLD模型中三相電流
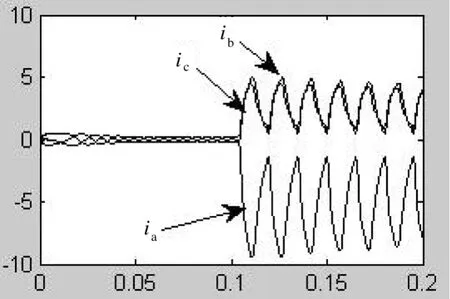
圖4 T1在t=0.1 s時三相電流殘差
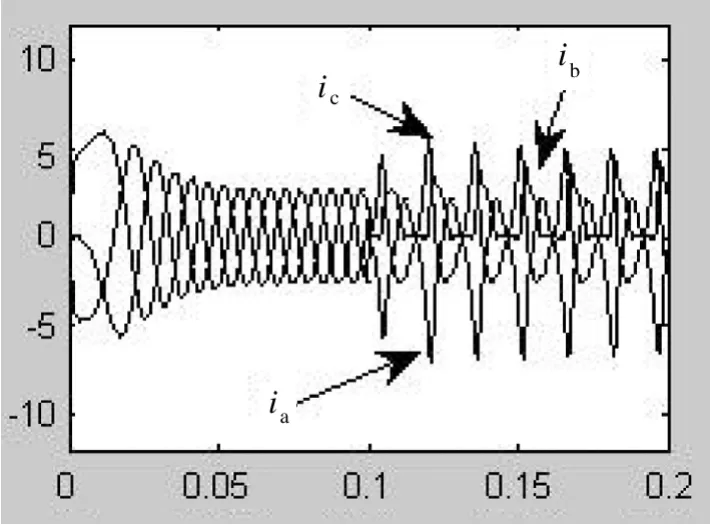
圖5 T2在t=0.1 s故障時三相電流
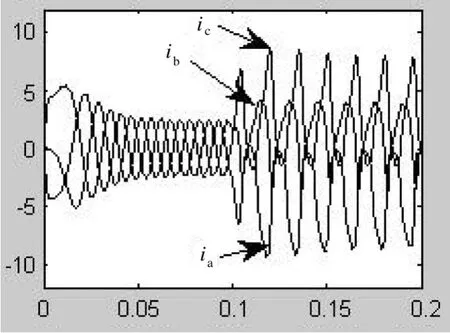
圖6 T2在t=0.1 s故障時MLD模型中三相電流

圖7 T2在t=0.1 s時三相電流殘差
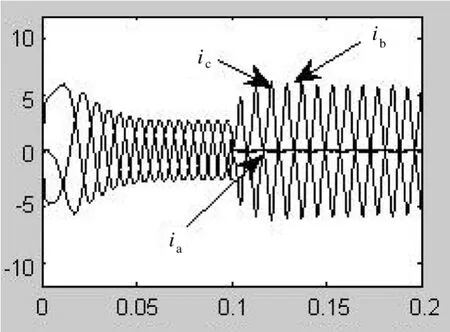
圖8 T1和T2同時在t=0.1 s故障時三相電流
從T1在0.1 s發生開路故障時的仿真結果可以看出,當T1反生開路故障時,三相電流殘差基本符合這說明MLD模型能準確描述實際系統故障時的狀態。
從T2在0.1 s發生開路故障時的仿真結果可以看出,當T2發生開路故障時,三相電流殘差基本符合這說明MLD模型能準確描述實際系統故障時的狀態。
從T1和T2在0.1 s同時發生開路故障時的仿真結果可以看出,當T1反生故障時,三相電流殘差基本符合正負值交替變化。這說明MLD模型能準確描述實際系統故障時的狀態。
3 結語
本文在對逆變器和電機工作模式分析的基礎上,建立了逆變器和電機的混雜系統模型,利用實際系統與MLD模型狀態估計器之間的輸出產生殘差,建立系統的狀態的殘差方程,仿真結果表明利用MLD模型建立的電機驅動系統MLD模型能夠準確地描述實際系統的狀態,利用MLD模型構建的殘差方程仿真結果與理論十分接近,對逆變電路的故障檢測診斷提供了一種行之有效的建模方法。
Modeling and Simulation for Inverter and Motor Based on Mixed Logical Dynamical Model
LUO Kai,CUI Bo-wen
(Jimei University,Xiamen361021,China)
Inverter circuit is a continuous state variable is driven by a discrete control signal with time evolution of a typical hybrid system,traditional modeling method based on mathematical model only consider the system either ignore discrete control change the state of continuous change of the system,and the ignored either considering only the system state of continuous change of discrete control system change,it is very easy to cause the loss of fault information is important,greatly influence the real-time performance and reliability of fault diagnosis.This paper has established the mixed logic dynamic model of inverter and motor through the analysis of the mode of the inverter and motor system,and using MATLAB/SIMULINK to simulation analysis the fault mode of inverter and motor,the simulation results shows that the method is very good to describe the output characteristics of system when inverter fault,provide accurate fault information for subsequent fault diagnosis.
inverter circuit;mixed logic dynamic model;fault mode;simulation
TM464 TM346
A
1009-9492(2015)10-0066-04
10.3969/j.issn.1009-9492.2015.10.016
2015-04-15

