再入飛行器等離子體預測與氣體組分相關性

苗文博，黃 飛，程曉麗，俞繼軍

（中國航天空氣動力技術研究院，北京 100074）

文章編號：1001?246X（2015）01?0027?06

再入飛行器等離子體預測與氣體組分相關性

苗文博，黃 飛?，程曉麗，俞繼軍

（中國航天空氣動力技術研究院，北京 100074）

對一類大鈍頭再入飛行器，理論分析電子密度預測與氣體組分的相關性，使用經驗證的數值模擬方法研究化學反應模型對等離子體預測的影響.研究發現：馬赫數是影響等離子體預測與氣體組分相關性的重要參數，馬赫數越高，不同氣體組分模型所得電子密度差異越大.氣體組分模型對等離子體預測的影響在駐點強壓縮區域和身部位置基本一致.對于大鈍頭再入飛行器，高度H＝60 km，馬赫數大于23時應該采用11組分化學反應模型.

再入飛行器；等離子體；氣體組分；化學反應模型；數值模擬

0 引言

當飛行器以高超聲速再入大氣層時，激波后溫度快速升高，達6 000 K～10 000 K，甚至10 000 K以上，氣體大量離解并伴隨電離反應進行.飛行器周圍產生高密度、強電離的等離子層，形成“等離子體鞘套”.這種“等離子體鞘套”對通信天線的電磁波信號形成屏蔽作用，進而產生“黑障”.“黑障”問題最先在航天器再入過程中發現，針對高超聲速再入飛行器在進入地球大氣時遇到的等離子體屏蔽問題，NASA基于Apollo探月工程進行了大量的理論分析、地面試驗以及飛行試驗研究，我國的探月和載人探月研究也會遇到類似的等離子體屏蔽問題.

等離子體由激波后氣體大量電離產生，實際飛行中，氣體電離程度受來流條件、壁面燒蝕引射產物等因素影響.Candler［1］、Ghislain［2］等人研究了不同飛行狀態下等離子體的分布規律，研究發現馬赫數越高，高度越低，電子密度越高.Scalabrin［3］針對高馬赫數狀態（Ma＞25）對比分析了不同的化學反應模型對電子密度預測影響，發現11組分反應動力學模型所得電子密度高于7組分，與飛行試驗結果更接近.程曉麗［4］在地面電弧風洞實驗研究了材料燒蝕對尾跡電子密度的影響，燒蝕將小幅降低尾跡電子密度.董維中［5］分析了再入體表面硅基材料燒蝕對電子密度的影響，燒蝕對頭部區域電子密度影響微弱，將降低身部及尾跡區電子密度.這些影響因素中，氣體組分及化學反應模型的選擇對電子密度預測的影響最顯著.高鐵鎖研究發現當飛行速度極高，激波后氣體溫度達10 000 K以上時，除了需要考慮NO＋離子還要考慮O＋離子對等離子體分布的影響［6］.Park［7］研究認為，11組分化學動力學模型可以更準確地模擬流場的化學反應過程，但是其同時帶來更大的計算成本.如何選擇盡可能少的氣體組分及相應的化學動力學模型，使得計算結果更準確，計算成本更低？本文基于平衡流假設和Gibbs自由能原理分析氣體組分與電子密度預測的相關性，并采用經驗證的數值模擬方法，分析了一類大鈍頭飛行器再入過程中，氣體組分及化學反應動力學模型對等離子體分布的影響規律和機理，獲得等離子體預測與氣體組分相關性的認識.

1 控制方程

求解的控制方程為三維化學反應完全N?S方程［8］，并基于以下假定：流動滿足化學非平衡及熱力學平衡；忽略輻射以及徹體力的影響；流動質量擴散采用雙組元氣體模型假設.三維化學反應完全N?S方程如下，其中連續性方程為各組元連續性方程，同時包含化學反應源項.

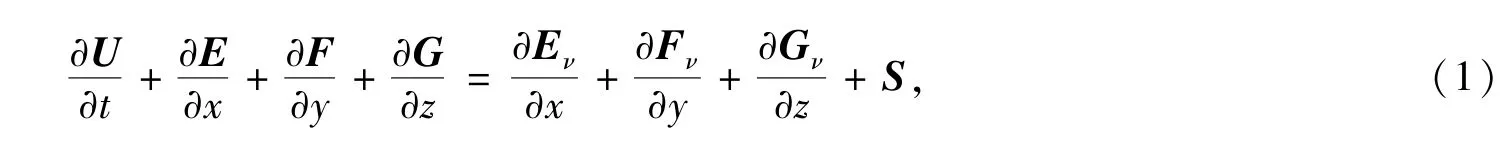
其中

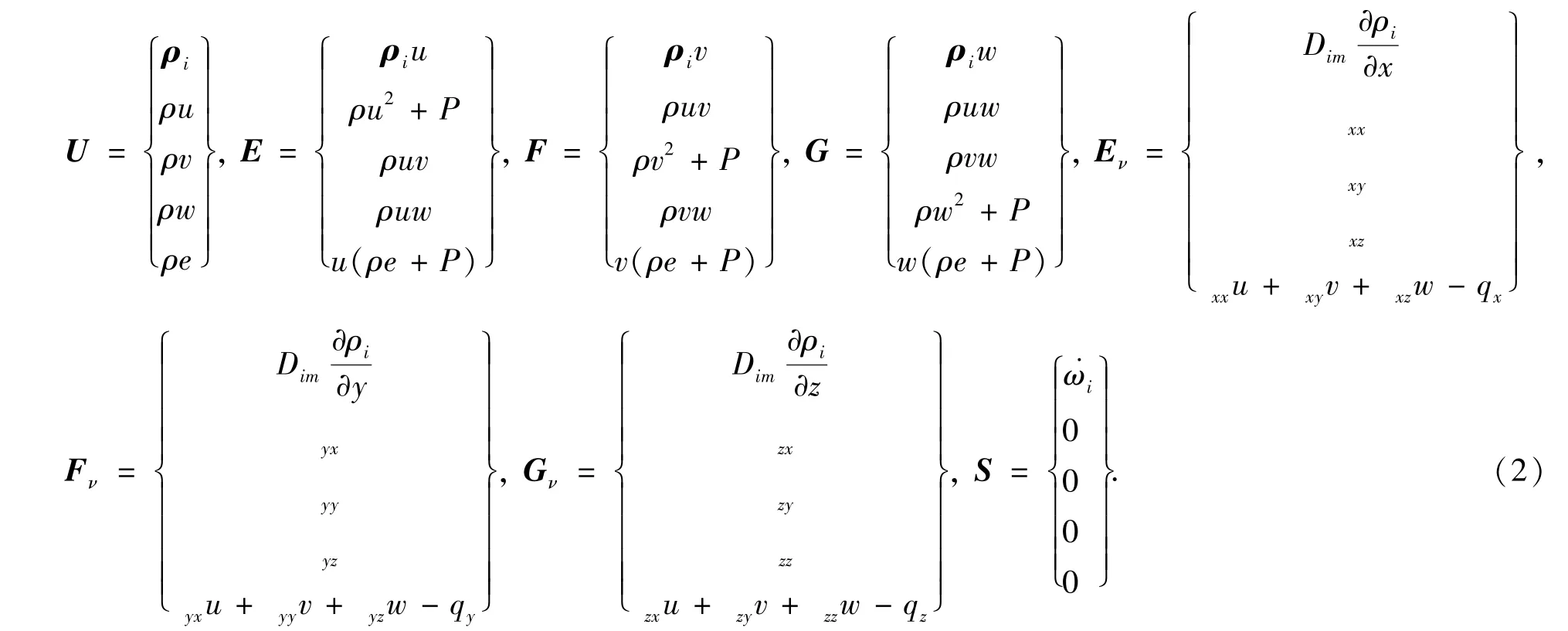
其中，ρi＝［ρ1，ρ2，…，ρns］T，ns為氣體組分的個數，ρ＝∑ρi為氣體總密度，u，v，w分別為x，y，z方向速度，P為壓強，e為單位質量的總能量．Dim為氣體組分i的等效擴散系數，為氣體組分i的化學反應生成項.

2 數值格式

選用具有較高流場分辨率的AUSM＋格式對控制方程進行離散.AUSM＋格式［9］的主要思想認為流場在傳播中存在對流影響與聲波影響，為分別考慮兩個過程，將無粘項分為對流項和壓力項進行處理，基于馬赫數對兩者分別進行特征分裂，是適用于化學反應流求解的一類高精度格式.下面給出其通量表達式.僅以項為例說明.

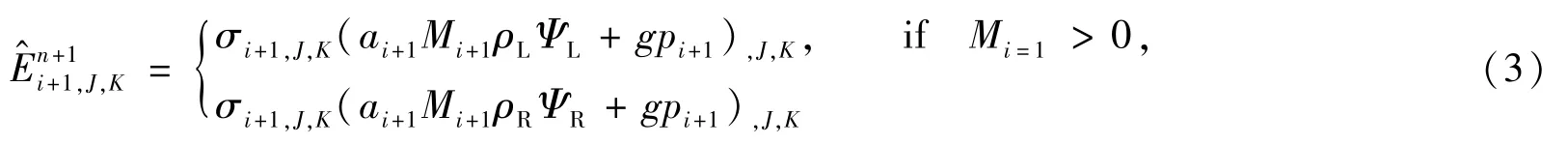
其中，Ψ＝（ci，u，v，w，H），g＝（ci，nx，ny，nz，0），其中下標i＋1表征界面參數，L和R分別表征左右臨近界面參數.

3 數學物理模型

進行流場以及電子密度場求解時分別使用了7組分7反應模型和11組分20反應模型［10］.7組分模型考慮了N，O，N2，O2，NO，NO＋，e－7個組分，只考慮了NO分子的電離過程，11組分模型考慮了N，O，N2，O2，NO，NO＋，，，N＋，O＋，e－11個組分，同時考慮了NO，N2，O2，N，O這5種氣體組分的電離.

選擇雙子星再入飛行器進行電子密度預測與氣體組分的相關性分析，其具有和探月飛行器類似的倒鐘型布局特征.圖1給出飛行器基準外形幾何尺寸示意圖.

4 算法驗證

選擇RAM?CII飛行試驗結果對電子密度預測方法進行驗證［11］.RAM?CII飛行器是一個頭部半徑為0.152 4 m，半錐角為9°，長度為1.295 m的球錐體.選用非催化壁壁面條件，計算高度 H＝71 km，Ma＝25.9的飛行狀態，壁面溫度取Tw＝1 500 K，分別進行了7組分和11組分化學反應模型.此時，飛行器繞流流場中氣體充分電離.圖2給出該狀態下沿軸向的電子密度峰值分布對比.預測結果與實際飛行試驗測量結果及分布趨勢吻合較好.并且可以看到，對于該狀態，11組分預測結果比7組分預測結果大約1個量級.11組分模型預測結果高估峰值電子密度，而7組分模型預測結果低估峰值電子密度.

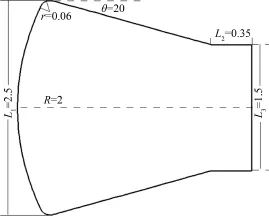
圖1 飛行器幾何尺寸示意圖Fig.1 Outline of the vehicle

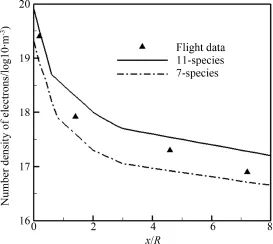
圖2 峰值電子密度沿流向對比Fig.2 Peak electron density along x direction

5 結果及分析

對于鈍頭再入飛行器，頭部駐點區域受強激波壓縮，化學反應非常劇烈，流動可以近似看作平衡流［12］.基于Gibbs自由能原理求解可以獲得激波后氣體平衡組分濃度分布［13］.通過對比氣體組分中離子的含量，可以確定影響等離子體分布的主要組分，從而為數值模擬的氣體組分選擇提供參考.此時，激波后氣體壓力由正激波關系式給出，激波后氣體總焓依據總能守恒原理由來流總焓給出.

表1給出高度H＝60 km多個馬赫數狀態下的平衡狀態正激波后氣體電離組分摩爾分數以及N＋，O＋，和離子之和對電子密度所做貢獻與NO＋所做貢獻之比.此處取N＋，O＋，和離子對電子密度的貢獻與NO＋離子貢獻之比?為參考量.由表1可以看到，對于高度H＝60 km，隨著馬赫數升高激波后氣體電離程度快速增加.在馬赫數M＝18時，?僅0.037 8，在馬赫數M＝25時，?已經超過1，預示此時N＋，O＋，和離子對電子密度的貢獻已超過NO＋離子，7組分氣體模型已經失效.

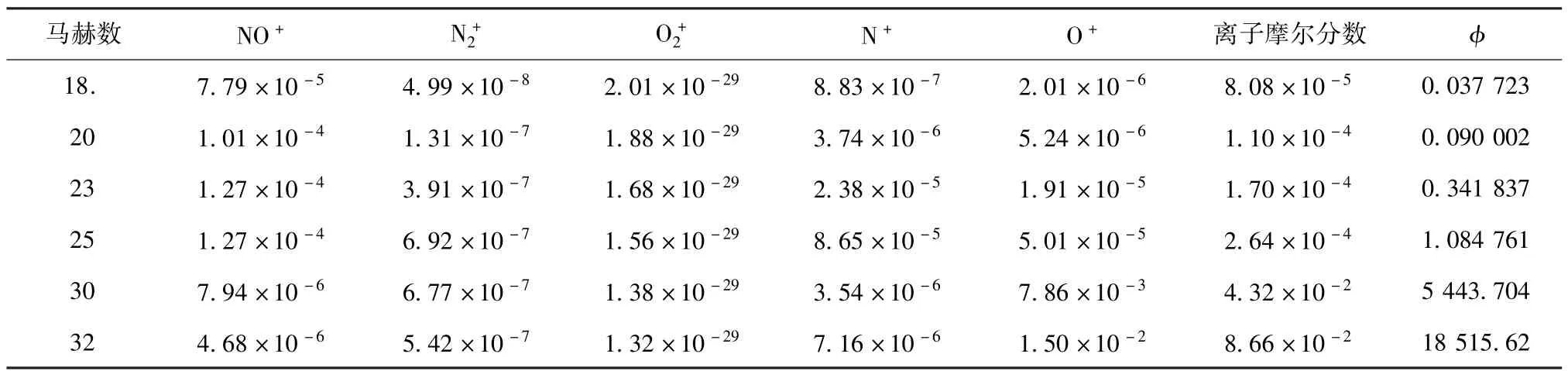
表1 H＝60 km處，平衡假設下激波后離子摩爾分數Table 1 M olar fraction of ions after the shock at H＝60 km

依據Gibbs自由能原理和駐點區域平衡流假設僅給出頭部強壓縮區域的氣體組分與等離子體預測隨來流條件變化的規律，對于身部以及尾跡區域同樣的規律是否依然存在？由于身部存在明顯的膨脹以及大分離流動，氣體平衡假設很難滿足，無法使用平衡流假設進行分析.以往研究表明，等離子體主要由頭部強壓縮區域產生，隨著流動逐漸向下游發展，上游的流動特征將對下游產生一定的影響.因此設置以下算例使用數值模擬的方法進行分析，高度H＝60 km，飛行攻角20°，飛行速度分別為10 km·s－1，7.0 km·s－1，5.5 km·s－1，對應的馬赫數分別為32.66，22.86和17.96.對這三個狀態分別使用7組分模型和11組分模型進行了數值模擬分析.

圖3給出3個狀態不同化學反應模型所得電子密度對比，可以看到在Ma＝17.96時，11組分模型所得電子密度略高于7組分模型，相差在5%以內，隨著馬赫數升高，11組分模型所得電子密度與7組分模型差異逐漸明顯，Ma＝22.86的時候不同化學反應模型所得電子密度相差30%左右，Ma＝32.66時不同化學反應模型差異1－2個量級.駐點區域數值預測所示規律與基于Gibbs自由能原理分析所得基本一致，在Ma＝23時，不同氣體組分所得電子密度差異已大于30%.這種差異在頭部強壓縮區域與身部大面積區域同時存在，不同位置的氣體組分對電子密度預測的影響規律一致，基于平衡流假設和Gibbs自由能原理可以獲得電子密度預測與氣體組分相關性較合理的認識.

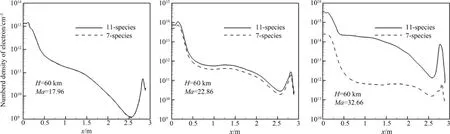
圖3 兩種化學反應模型迎風子午面峰值電子密度x方向分布Fig.3 Peak electron density along windward generatrix in chemical reaction models

對比發現，數值預測所得差異略小于理論分析所得，這主要是因為使用11組分化學反應模型時，激波后氣體內能除了用于激發NO＋電離之外還要用于激發N＋，O＋，和離子電離，而使用7組分化學反應模型時更多的能量用于NO＋電離，NO＋離子貢獻的電子密度要高于11組分反應時NO＋離子貢獻的電子密度.

駐點區域是流動化學反應最強烈的位置，對馬赫數Ma＝17.96和Ma＝32.66兩個狀態進一步分析不同化學反應模型的駐點線流場參數.圖4給出兩個狀態駐點線溫度分布，Ma＝32.66時，激波后氣體溫度在10 000 K左右，考慮N＋，O＋，和離子氣體電離過程使得更多的氣體內能轉化為化學能，降低了激波后氣體溫度，同時使得激波層更靠近壁面.而對于Ma＝17.96，激波后氣體溫度在6 000 K左右，氣體電離程度減弱，即使考慮更多的氣體電離過程仍對流場能量分布狀態影響微弱.

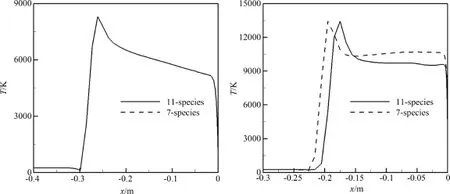
圖4 駐點線溫度分布（左：Ma＝17.96，右：Ma＝32.66）Fig.4 Temperature along stagnation line（left：Ma＝17.96，right：Ma＝32.66）

圖5給出2個狀態駐點線離子數密度分布對比.對于Ma＝32.66狀態，受高溫高壓作用，氣體電離以原子電離為主，N＋，O＋，和離子電離明顯，特別是N＋和O＋離子.對于Ma＝17.96狀態，N＋，O＋，和離子相比NO＋的電離程度微弱的多.可見當流場中N＋，O＋，和離子的電離度與NO＋相當或者高于NO＋離子時，必須考慮11組分化學反應模型.此處假定N＋，O＋，和離子的電離度與NO＋的電離度之比大于20%時，必須考慮11組分化學反應模型.由此可以認為，對于大鈍頭再入飛行器，當H＝60 km，馬赫數高于23的時候，應該選擇11組分化學反應模型進行電子密度預測.

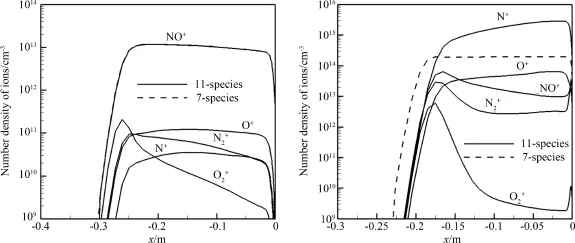
圖5 駐點線離子數密度分布（左：Ma＝17.96，右：Ma＝32.66）Fig.5 Number density of ions along stagnation line（left：Ma＝17.96，right：Ma＝32.66）

6 小結

高超聲速再入飛行器再入過程往往經歷“黑障”，要進行飛行器通信中斷邊界分析需要獲得準確的電子密度分布，本文使用數值模擬和理論分析手段研究了大鈍頭再入飛行器再入過程時氣體組分對電子密度預測的影響規律和機理.獲得以下結論：對于高馬赫數再入飛行狀態，馬赫數是影響氣體組分與電子密度預測相關性的重要參數，馬赫數越高，不同化學反應模型所得電子密度差異越大.氣體組分對等離子體預測的影響規律在駐點強壓縮區域和身部大面積區域一致，理論分析與數值模擬所得結論基本一致，可以通過理論分析快速選擇等離子體預測時的氣體組分模型.對于大鈍頭再入飛行器，高度H＝60 km，馬赫數Ma大于23時應考慮11組分化學反應模型.

［1］ Candler G V.The computational of weakly ionized flow in non?equilibrium［D］.California：Stanford University，1988.

［2］ Ghislain T.Numerical prediction ofweakly ionized high enthalpy flow in thermo?chemical non?equilibrium［R］.AIAA 2004－2462，2004.

［3］ Scalabrin L C，Boyd ID.Numerical simulation ofweakly ionized hypersonic flow for reentry configurations［R］.AIAA 2006－3773，2006.

［4］ Cheng X L，Dong Y H，Li T L.Computational and experimental studies of ablation effect on electronic characteristics in vehicle wake［J］.Acta Aeronautica et Astronautica Sinica，2007，28（4）：796－780.

［5］ DongW Z，Gao T S，Ding M S，Jiang T.Numerical analysis for the effect of silicon based material ablation on the flowfield around re?entry blunt body［J］.Acta Aerodynamica Sinica，2010，28（6）：708－714.

［6］ Gao TS，DongW Z，Ding M S.The effects of physicochemicalmodels on distribution of plasma in high temperature flow field ［J］.Acta Aerodynamica Sinica，2013，31（5）：541－545.

［7］ Park C，Griffith W，Nonequilibrium hypersonic aerothermodynamics［M］.New York：Wiley，1990.

［8］ 歐陽水吾，高溫非平衡空氣繞流［M］.北京：國防工業出版社，2001.

［9］ Liou M S.A further developmentof the AUSM＋scheme towards robustand accurate solutions for all speeds［R］.AIAA Paper 2003－4116，2003.

［10］ Gnoffo P A，Gupta R N，Shinn J L.Conservation equations and physical models for hypersonic air flows in thermal andchemical non?equilibrium［R］.NASA TP－2867，1986.

［11］ Scbexnayder C J，Huber P W，Evans J S.Calculation of electron concentration for a blunt body at orbital speed and comparison with experimental data［R］.NASA TN?D－6294，1971.

［12］ Park C，Howe JT，Jaffe R L.Review of chemical?kinetic problems of future NASAmissions，I：Earth entries［J］.Journalof Thermo?physics and Heat Transfer，1993，7（3）：383－392.

［13］ Liu X Z.Numerical simulation of hypersonic thermochemical equilibrium flows［D］.Beijing：China Academy of Aerospace Aerodynamics，1994.

Plasma Prediction of Reentry Vehicle and Gas Com ponents

MIAOWenbo，HUANG Fei，CHENG Xiaoli，YU Jijun
（China Academy ofAerospace and Aerodynamics，P．O．Box 7201?16，Beijing 100074，China）

Hypersonic flows around a bluntbody are studied with numerical simulation and theoretical analysis.Correlations between plasma prediction and gas components are obtained.It shows that it is Mach number which affects the peak number density of electrons.Numerical simulation agreeswith theoretical analysis well.Differences between two gasmodels get greater as Mach number increases.The differences follow same trend at back taper with stagnation region.A 11?species chemicalmodel should be applied to increase accuracy when reentry capsule flight at height of60 km and Mach number is over 23.

reentry vehicle；plasma；gas components；chemical reaction model；numerical simulation

V211.3

A

2013－12－30；

2014－04－11

苗文博（1980－），男，博士，高級工程師，主要從事非平衡流研究，E?mail：tingles＠126.com

?通訊作者：黃飛（1982－），高級工程師，E?mail：huang05013＠163.com

Received date： 2013－12－30；Revised date： 2014－04－11