應用于反應堆熱工水力程序的核態沸騰傳熱關系式評價

李美琳，林 萌，楊燕華，張 昊，龔 湛

（1.上海交通大學核能科學與工程學院，上海200240；2.國家核電技術有限公司北京軟件技術中心，北京100029）

COSINE程序是我國自主開發的核電廠設計與安全分析軟件之一［1］，主要由求解器、本構關系、熱構件和水力學構件等幾部分組成。其中，本構關系描述流體之間或流體與壁面之間相互作用，包括壁面傳熱和摩擦、相間傳熱和摩擦、局部阻力等內容，主要用于封閉守恒方程，其準確性對于程序計算結果的正確性影響很大。而且在核電站中堆芯燃料棒與冷卻劑之間、穩壓器內加熱元件與流體之間、蒸汽發生器U形管兩側及壓力容器外部冷卻（ERVC）等主要都是通過壁面傳熱進行換熱工作的，所以本構關系中的壁面傳熱模型對于反應堆熱工水力程序計算的準確性非常重要。且流體流經燃料棒表面等壁面時，壁面溫度等參數會不斷變化，流體與壁面間的傳熱模式也就不斷變化。正常運行工況下反應堆系統主要發生臨界前壁面傳熱，其中，核態沸騰傳熱因應用多、機理復雜且傳熱關系式相差大，最值得研究，所以本文的研究對象為過冷和飽和核態沸騰傳熱。

壁面傳熱原理十分復雜，多數情況下會使用實驗關聯式計算，而實驗關聯式受參數適用范圍影響很大，超出范圍便可能不適用。COSINE程序要選擇適用于國內反應堆包括先進反應堆的核態沸騰傳熱關系式，可以借鑒目前已有的反應堆系統熱工水力程序中常用的核態沸騰關系式。它們的適用范圍見表1。我國主要堆型為壓水堆，反應堆系統中可能發生核態沸騰的工況中，如蒸汽發生器二次側換熱等工況基本處于表1中部分關系式的適用范圍內，其實驗也相對較易進行，相關研究相對較多，可以直接使用適用范圍包括該工況的關系式或通過已有實驗驗證后再選擇，這里不再進行研究；但有些特殊工況如燃料棒與冷卻劑的核態沸騰換熱和ERVC工況下，壓力分別為15.5MPa和0.1MPa，特征尺寸分別為0.01m和4m左右，由于這兩種工況不在任一關系式的適用范圍內；兩種工況的壓力高或特征尺寸大，驗證實驗并不容易進行，實驗數據不易獲得；兩種工況較特殊，ERVC為先進反應堆才有的現象，相關研究相對不是很多等原因，不能直接選擇關系式或直接進行實驗驗證。所以有必要對備選關系式進行預先的評價，對各關系式結果差異大的范圍建議在程序中設置用戶選項，可以讓用戶自行選擇關系式；同時為后期實驗驗證提供參考意見，使實驗更具針對性。考慮到目前已有的反應堆系統熱工水力程序中常用的核態沸騰關系式不僅較廣泛地應用于反應堆系統程序，而且也被應用于具有大特征尺寸的安全殼程序，最有必要作為首要研究對象，因此本文重點研究這些關系式在這兩種工況下的計算結果。

為了對應用于反應堆熱工水力程序的核態沸騰傳熱關系式進行評價，本文將先借助一般工況下的實驗數據研究影響核態沸騰傳熱量的各參數變化對結果的一般影響規律，再研究核電廠兩種特殊的核態沸騰工況，即燃料棒表面核態沸騰換熱和ERVC工況下計算結果隨參數變化規律、不同關系式計算結果間差異大小、不同區域內參數敏感性大小等內容。

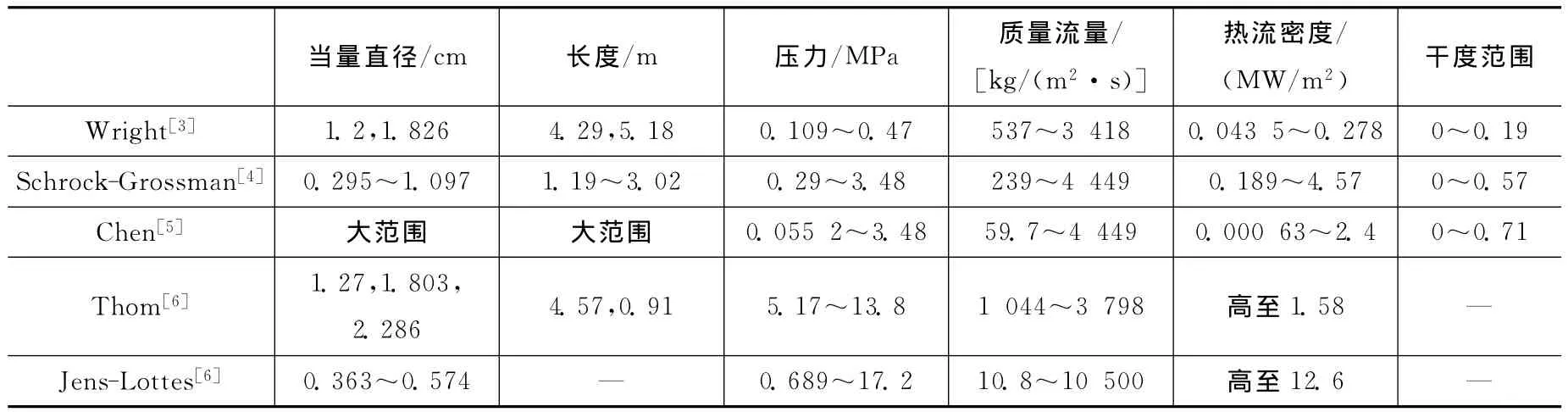
表1 核態沸騰關系式適用范圍比較［2］Table 1 Range of application of nucleate boiling correlations

1 一般工況核態沸騰傳熱量隨參數變化特性

幾種反應堆系統熱工水力程序常用的核態沸騰傳熱關系式見附錄。可以看出，核態沸騰傳熱量主要受壁面過熱度、干度、質量流速、當量直徑、壓力和流體溫度等參數影響。應用控制變量法研究各參數變化后結果的變化情況。

由于沒有在兩種特殊工況下的實驗數據，本節將先利用一般工況下的實驗數據研究一般工況下核態沸騰傳熱量隨各參數變化規律，作為特殊工況下變化規律的一種參考，但不同工況變化特性可能不同，不能將其當做絕對的結論。

傳熱量隨過熱度變化規律的實驗研究相對較多，一般均呈傳熱量隨過熱度增加而增大的趨勢［5，6，9-11］；傳熱量具有低干度時不隨干度變化，高干度時隨干度增加而增大的規律［9，12-15］；傳熱量具有低干度時不隨質量流速變化，高干度時隨質量流速增加而增大的規律［9，10，12，15，16］。鑒于針對傳熱量隨其他參數變化趨勢的研究相對較少，暫不將它們作為一種普遍規律列出。上述一般工況下較普遍的規律也只是作為后續研究的一種參考。

2 兩種特殊核態沸騰工況下計算結果分析

本節將研究各關系式計算結果隨過熱度、干度、質量流速、當量直徑、壓力和流體溫度等變化情況，參數變化范圍內各關系式計算結果間差異大小及計算結果隨參數變化的敏感性。由于要研究的燃料棒-冷卻劑換熱和ERVC兩種工況環境壓力分別為高壓和常壓，壓力一般為常量，且主流溫度主要分過冷和飽和兩種類型，所以本節將分高壓飽和、高壓過冷、常壓飽和、常壓過冷四種情況研究其他參數變化時對計算結果的影響，及高壓和常壓時流體是否過冷對其造成的影響。

根據反應堆堆芯參數范圍，設計燃料棒-冷卻劑換熱工況（以下簡稱高壓工況）的標準工況取壓水堆壓力P=15.5MPa，燃料棒直徑D=0.01m，堆芯質量流速G=3 000.0kg／（m2·s）［17］，干度x=0.1，壁溫Tw=620K，飽和時主流溫度Tl=617.91K，過冷時主流溫度取堆芯流體平均溫度Tl=573K；根據ERVC工況（以下簡稱常壓工況）時的參數范圍，設計常壓標準工況取大氣壓P=0.1MPa，當量直徑估值D=4.0m，質量流速G=60.0kg／（m2·s），干度x=0.1，壁溫Tw=375K，飽和時主流溫度Tl=372.782K，過冷時流體溫度取室溫Tl=300K。參數變化范圍要覆蓋以上兩種工況，取當量直徑D：0.01～4.5m，質量流速G：0～5 000.0kg／（m2·s），由于核態沸騰干度和過熱度沒有明確范圍，所以范圍取的較大，干度x：0～0.95，過熱度dT：0～100K。前述計算工況不在任一關聯式適用范圍內，不能針對關聯式適用范圍比較其適用性，所以這里均在全范圍內對關聯式適用性進行重新研究。

2.1 干度

如前所述，由于核態沸騰干度沒有明確范圍，本節研究的干度變化范圍選取較大為0～0.95，但一般小于0.7的干度范圍內結果相對更有意義，高干度范圍的結果列出僅供參考。

圖1表明過冷工況計算結果差異很大，尤其是高干度區域差異更大，Schrock-grossman1［8］、Schrock-grossman2［4］、Wright［3］計算結果較其他大很多。

Schrock-grossman1、Schrock-grossman2、Wright計算結果隨干度增加先增大后減小，在干度為0.8左右存在峰值；Rohsenow［7］、Jens-Lottes［6］、Thom［6］、Forster-Zuber［5］不隨干度變化；Chen［5］在飽和時存在峰值，過冷時隨干度增加傳熱量減小。一般工況下核態沸騰實驗數據顯示傳熱量有在干度較小時不隨干度變化，干度稍大時隨干度增加而增大的趨勢，所以特殊工況下傳熱量隨干度增加呈增大或不變的趨勢均為可能現象；而在干度很大時作者認為由于氣相傳熱能力小于液相，傳熱量隨其增加而減小較合理。

2.2 質量流速

圖2顯示常壓和高壓過冷工況各關系式計算結果差異最大，Jens-Lottes、Thom公式較其他方法計算結果相差較大，其他計算方法在質量流速較小時較接近，質量流速增大后差異增加。

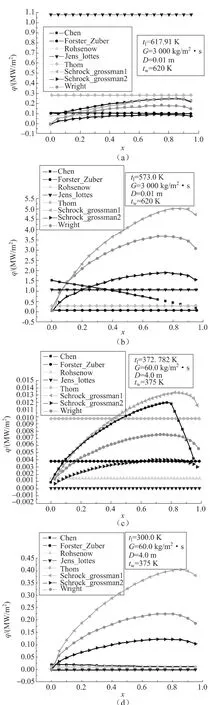
圖1 熱流密度隨干度變化曲線Fig.1 The trend of heat flux versus quality

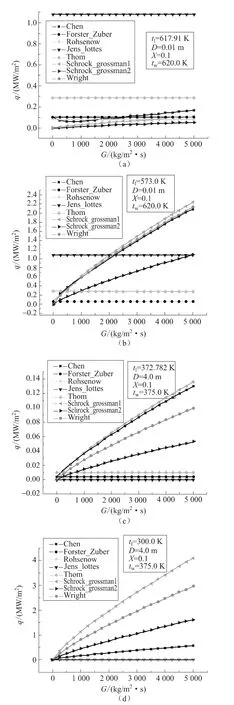
圖2 熱流密度隨質量流速變化曲線Fig.2 The trend of heat flux versus mass flux

Jens-Lottes、Rohsenow、Thom、Forster-Zuber公式不受質量流速影響，其他公式結果基本隨質量流速增加而增大。上節實驗結果顯示一般工況下傳熱量具有低干度時不隨質量流速增加而變化，高干度時隨質量流速增加而增大的趨勢，特殊工況下傳熱量呈隨干度增加而增大或不變化的趨勢均為可能現象。

2.3 壁面過熱度

壁面過熱度的研究范圍為0～100K，大于100K之后傳熱模式為臨界后傳熱，但一般核態沸騰過熱度要小于100K，且沒有明確邊界值，所以這里列出高過熱度區結果作為參考，著重比較小過熱度區域的計算結果。

圖3顯示Jens-Lottes、Rohsenow計算結果遠大于其他關系式的計算結果，過熱度小時計算結果較接近，過熱度大時結果相差很大，高壓時Jens-Lottes計算結果隨過熱度增加可達106MW／m2量級以上，Rohsenow、Thom、Forster-Zuber計算結果也在幾十MW／m2以上，基本超過了一般情況下反應堆核態沸騰熱流密度幾MW／m2的量級。

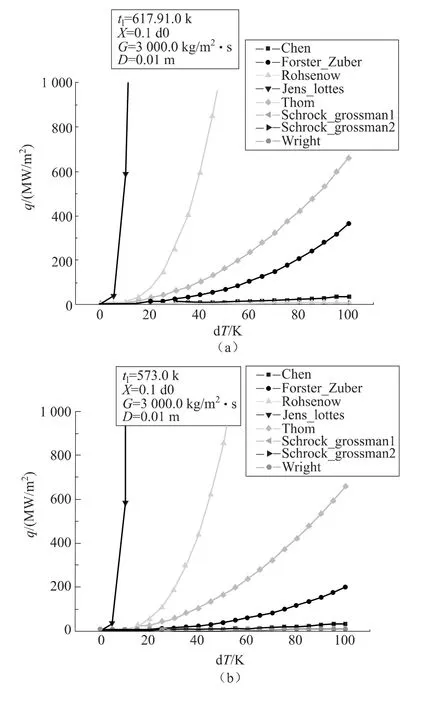
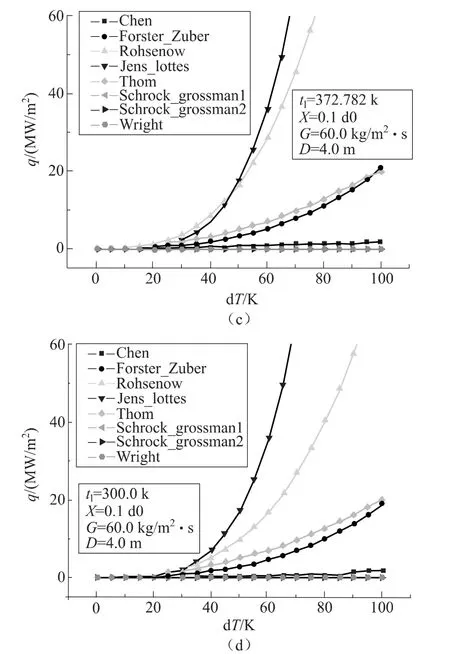
圖3 熱流密度隨壁面過熱度變化曲線Fig.3 The trend of heat flux versus degree of superheat

Jens-Lottes隨過熱度增加迅速增加，敏感性很大，Rohsenow、Thom、Forster-Zuber對過熱度敏感性也很大，在過熱度大于20K時結果急速增大，其他公式計算結果隨過熱度增加平穩增大。上節實驗數據顯示一般工況傳熱量隨過熱度增加而增大，且過熱度增加驅動力增大傳熱量增加較合理，所以計算結果隨過熱度增加而增大基本是正確的。

2.4 當量直徑

圖4顯示Jens-Lottes和Thom公式與其他關系式計算結果相差較大，其他公式結果比較相近，當量直徑小時比當量直徑大時公式間差異大。

在當量直徑小于1m時Chen、Wright、Schrock-grossman1、Schrock-grossman2計算結果隨當量直徑增加急劇減小，對其敏感性很大，Rohsenow、Jens-Lottes、Thom、Forster-Zuber計算結果不隨當量直徑變化；在當量直徑較大時各關系式計算結果均隨其變化很小。

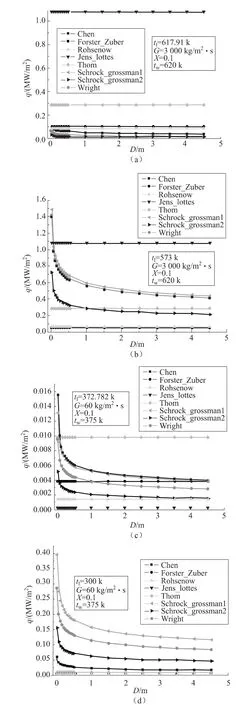
圖4 熱流密度隨當量直徑變化曲線Fig.4 The trend of heat flux versus equivalent diameter

2.5 主流溫度影響

分析以上幾組計算結果可以發現過冷工況相對飽和工況各關系式計算結果差異更大。Jens-Lottes和Thom不受過冷影響，Rohsenow、Forster-Zuber受過冷影響較小。Rohsenow和Forster-Zuber計算結果在高過熱度等情況下甚至出現隨主流溫度降低而減小的現象，其他公式結果隨流體溫度降低而增大，且在高干度、高質量流速、小當量直徑時及常壓時受流體溫度影響更大。作者認為流體溫度降低，帶走壁面熱量增加，壁面傳熱量增大較為合理。

3 關系式評價及建議

3.1 燃料棒-冷卻劑核態沸騰換熱工況分析

對燃料棒-冷卻劑核態沸騰換熱工況，即上述的高壓過冷工況來說，過熱度增加后結果變化最大，計算結果間差異最大，熱流密度值也非常大，最需要進行實驗研究。其次，干度變化引起的結果變化也較大。Jens-Lottes公式計算結果普遍偏大，與其他關系式計算結果一般相差較大。總體而言，Chen、Schrock-Grossman1、Schrock-Grossman2和Wright公式計算結果隨干度、質量流速、過熱度變化趨勢相對較合理，不會出現結果過高或隨參數變化率過高現象，更加利于程序穩定，相對更適用于堆芯燃料棒壁面核態沸騰傳熱工況的程序計算。

3.2 ERVC工況分析

對ERVC工況，即上述的常壓過冷工況來說，除了高過熱度區域最值得研究外，由于質量流速增加時計算結果間差異很大，也應進行實驗研究。總體而言，對ERVC工況來說也是Chen、Schrock-Grossman1、Schrock-Grossman2和Wright公式計算結果隨干度、質量流速、過熱度變化趨勢比較合理，不會出現結果過高或隨參數變化率過高現象，更加利于程序穩定，更適于程序選擇。

3.3 小當量直徑工況的分析

當量直徑小時計算結果對當量直徑敏感性很高，結果間差異也相對較大，所以像反應堆堆芯燃料棒壁面核態沸騰傳熱這種小當量直徑工況相對大當量直徑工況更需要進行驗證或在程序計算中設置用戶選項。

4 結論

本文對幾種常用于反應堆系統的核態沸騰傳熱關系式在兩種特殊的反應堆系統核態沸騰傳熱工況下的計算結果隨影響參數變化情況進行研究，研究了變化趨勢的合理性，比較了在不同范圍內各關系式計算結果間的差異程度和參數敏感性，得出的主要結論為Chen、Schrock-Grossman1、Schrock-Grossman2和Wright公式相對更適用于反應堆熱工水力分析程序中這兩種工況下核態沸騰的計算。在選擇應用于堆芯燃料棒壁面核態沸騰傳熱的關系式時最應進行高過熱度和干度增加的實驗；選擇應用于ERVC核態沸騰的傳熱關系式時最應進行高過熱度和質量流速增加的實驗，因為在這些范圍內各關系式計算結果差異最大。

附錄 核態沸騰計算關系式

［1］ Yang Yanhua.Requirement analysis and primary design of COSINE code［C］／／Proceeding of American Nuclear Society Annual Meeting.［s.1.］：［s.n.］，2012.

［2］ Anh T.Mai.Thermal Hydraulic and Fuel Performance Analysis for Innovative Small Light Water Reactor Using VIPRE-01and FRAPCON-3［EB／OL］.Oregon：Oregon State University，2011.http：／／hdl.handle.net／1957／26964.

［3］ R.M.Wright.Downflow forced-convection boiling of water in uniformly heated tubes［M］.California：University of California，Berkeley，1961.

［4］ Jianyun Shuai.Flow Boiling Heat Transfer in Narrow Vertical Channels［M］.Goettingen：Cuvillier Verlag，2004.

［5］ The RELAP5Code Development Team.RELAP5／MOD3 CODE MANUAL VOLUME IV：MODELS AND CORRELATIONS［M］.Idaho：Idaho National Engineering Laboratory，Lockheed Idaho Technologies Company，1995，（4）：57-128.

［6］ 潘欽.沸騰熱傳與兩相流［M］.臺北：國立編譯館，2001：186-222.

［7］ W.M.Rohsenow.A Method of Correlation Heat Transfer Data for Surface Boiling of Liquids［J］.Heat Transfer，1952，74（4）：969-973.

［8］ 魯鐘琪.兩相流與沸騰傳熱［M］.北京：清華大學出版社，2002：212-222.

［9］ T.N.Tran，M.W.Wambsganss，D.M.France.Small circular-and rectangular-channel boiling with two refrigerants［J］.Multiphase Flow，1996，22（3）：485-498.

［10］ 唐琦琳.管束外垂直上升汽液兩相流沸騰傳熱特性的實驗研究［D］.上海：上海交通大學，2007.

［11］ Peter Griffith，John D.Wallis.The role of surface conditions in nucleate boiling［R］.Washington：the Office of Naval Research，1958.

［12］ K.Aroonrat，A.S.Dalkilic，S.Wongwises.Experimental study on evaporative heat transfer and pressure drop of R-134aflowing downward through vertical corrugated tubes with different corrugation pitches［J］.Experimental Heat Transfer.2013，26：41-63.

［13］ Peter A.Kew，Keith Cornwell.Correlations for the prediction of boiling heat transfer in small-diameter［J］.Applied Thermal Engineering，1997，17：705-715.

［14］ B.Thonon，A.Feldman，L.Margat，C.Marviilet.Transition from nucleate boiling to convective boiling in compact heat exchangers［J］.Refrig，1997，20（8）：592-597.

［15］ A.Feldman，C.Marvillet，M.Lebouche.Nucleate and convective boiling in plate fin heat exchangers［J］.International Journal of Heat and Mass Transfer，2000，43：3433-3442.

［16］ 沈秀中，宮崎慶次，徐濟鋆.在垂直環形窄縫流道中的沸騰傳熱特性研究［J］.核科學與工程，2001，21（3）：244-251.

［17］ 林誠格，郁祖盛，歐陽予.非能動安全先進核電廠AP1000［M］.北京：原子能出版社，2008.