基于BP 神經網絡的住宅項目工程造價估算模型研究

劉嘉威 同濟大學 經濟與管理學院，上海 201804

在住宅項目中，項目前期的投資估算是較為重要的一環。投資估算是整個項目投資控制的起點，是實施階段投資控制的基礎。同時，投資估算也是業主對于項目方案是否可行的重要評價依據，對于業主融資方式的選取以及招標方案的選擇也有重要意義。因此，采用合適的方法快速準確地估算出住宅項目的造價對于業主而言有著極為重要的現實意義。

大量住宅項目的資料表明，住宅項目的造價與工程特征因素之間存在聯系，這種聯系表現為高度的非線性和不確定性。而BP 神經網絡是一種智能仿生模型，具有自組織、自適應、非線性映射能力以及高容錯性，能夠完成任意復雜函數關系的映射。因此本文將利用已建住宅項目的資料，選取影響住宅造價的主要工程特征因素，然后選取若干已竣工備案的相似住宅工程，利用這些工程的數據，在Matlab R2012a 環境下對BP 神經網絡進行訓練，建立住宅造價與各工程特征因素間的關系模型，并借助建立的模型對住宅項目造價進行估算，通過估算造價與實際造價的比較，分析模型是否可行。

1 BP 神經網絡模型的建立

1.1 BP 神經網絡原理

BP 神經網絡有輸入層、隱含層和輸出層，網絡由兩部分組成:信息的正向傳遞與誤差的反向傳播。在正向傳遞中，輸入信息從輸入層經隱含層逐層計算傳向輸出層，如果在輸出層沒有得到期望的輸出，則計算輸出層的誤差值，然后反向傳播，通過網絡將誤差信號沿原來的連通路反傳回來，修改各層神經元的權值直至達到期望目標。

1.2 網絡結構的選取

輸入層單元數的選取與影響造價的主要工程特征因素有關，本模型中選取工程因素為結構類型、土方工程、基礎類型、砌筑工程、門窗工程、內墻裝飾、外墻裝飾、樓地面工程、安裝工程、建筑層數、建筑面積，故選擇輸入層的單元數為11。

為了更加直觀地得出模型估算出的造價值，可以將輸出層輸出的信息選擇為住宅項目的工程造價，因此，選擇輸出層的單元數為1。

1.3 模型自變量數據的處理

由于BP 神經網絡的輸入數據必須為實數，而自變量中除了建筑層數和建筑面積均為定性因素，故首先需要對這些自變量進行定量化處理。自變量的定量化處理規則如表1 所示。

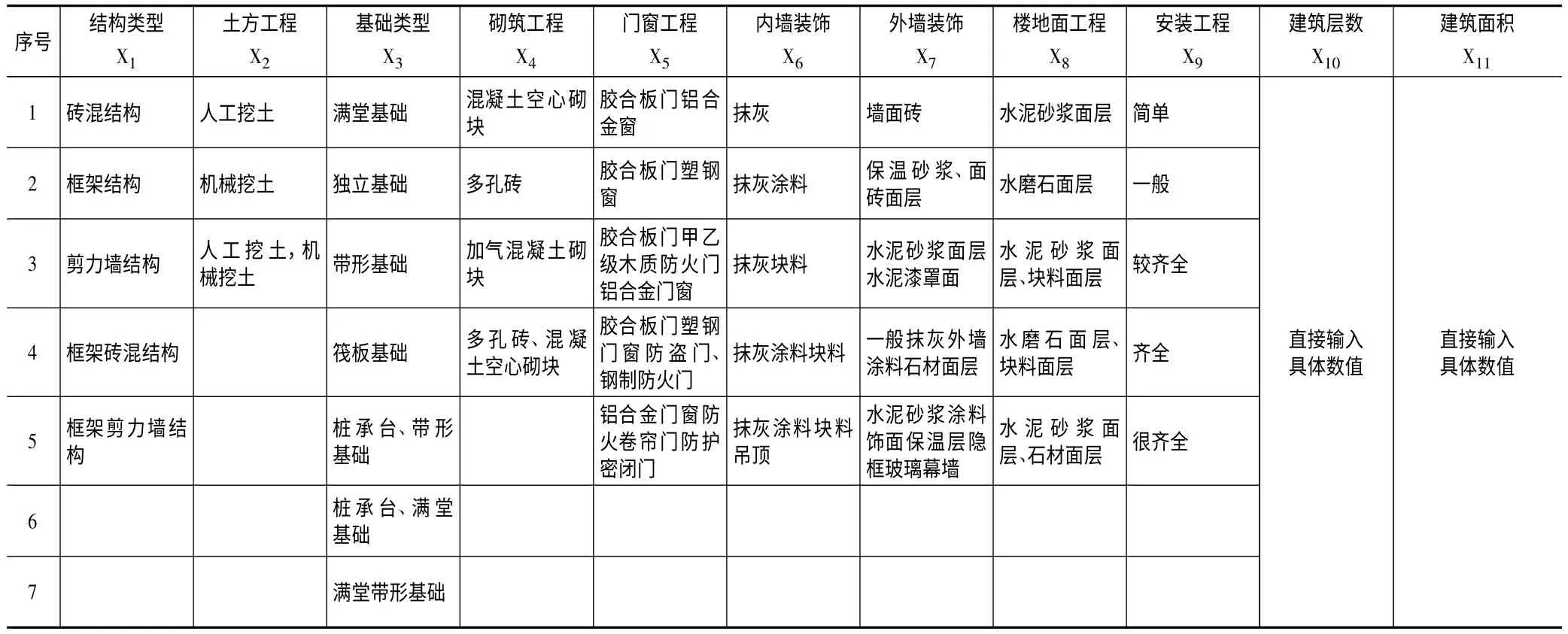
表1 自變量的定量化處理規則

1.4 BP 神經網絡模型的訓練

1.4.1 信息的正向傳遞

設Xj表示輸入層第j 個單元的輸入，j=1，2…，L;wij表示隱含層第i 個單元到輸入層第j 個單元的權值;θj表示隱含層第i 個單元的閾值;wki表示輸出層第k 個單元到隱含層第i 個單元之間的權值;αk表示輸出層第k 個單元的閾值，k=1，2，…，N;Ok表示輸出層第k 個單元的輸出，tk為輸出層第k 個單元的期望輸出，p 為樣本數，所有樣本的誤差為E，no為迭代次數。

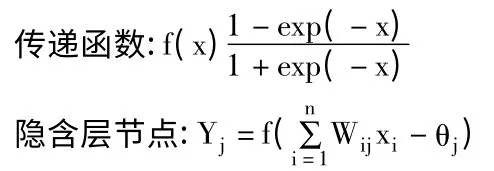
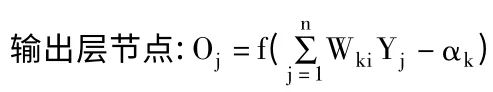
樣本輸出點的誤差為:

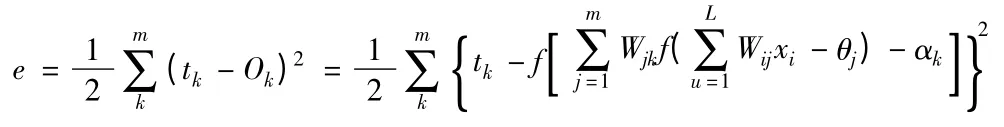
1.4.2 誤差的反向傳播

輸出層節點與隱含層節點間，誤差計算公式為:

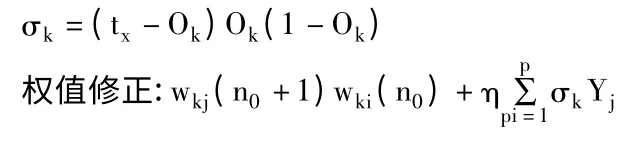
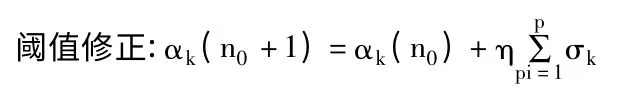
輸入層節點與隱含層節點之間，誤差計算公式為:

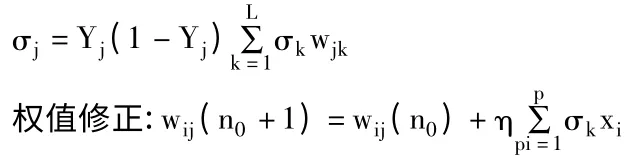
2 實例仿真與結果分析

2.1 數據樣本的獲取

本實例以北方某城市2013-2014 年間竣工驗收的18 個住宅項目的原始數據為樣本，數據按表1 中的規則進行定量化處理之后如表2所示。

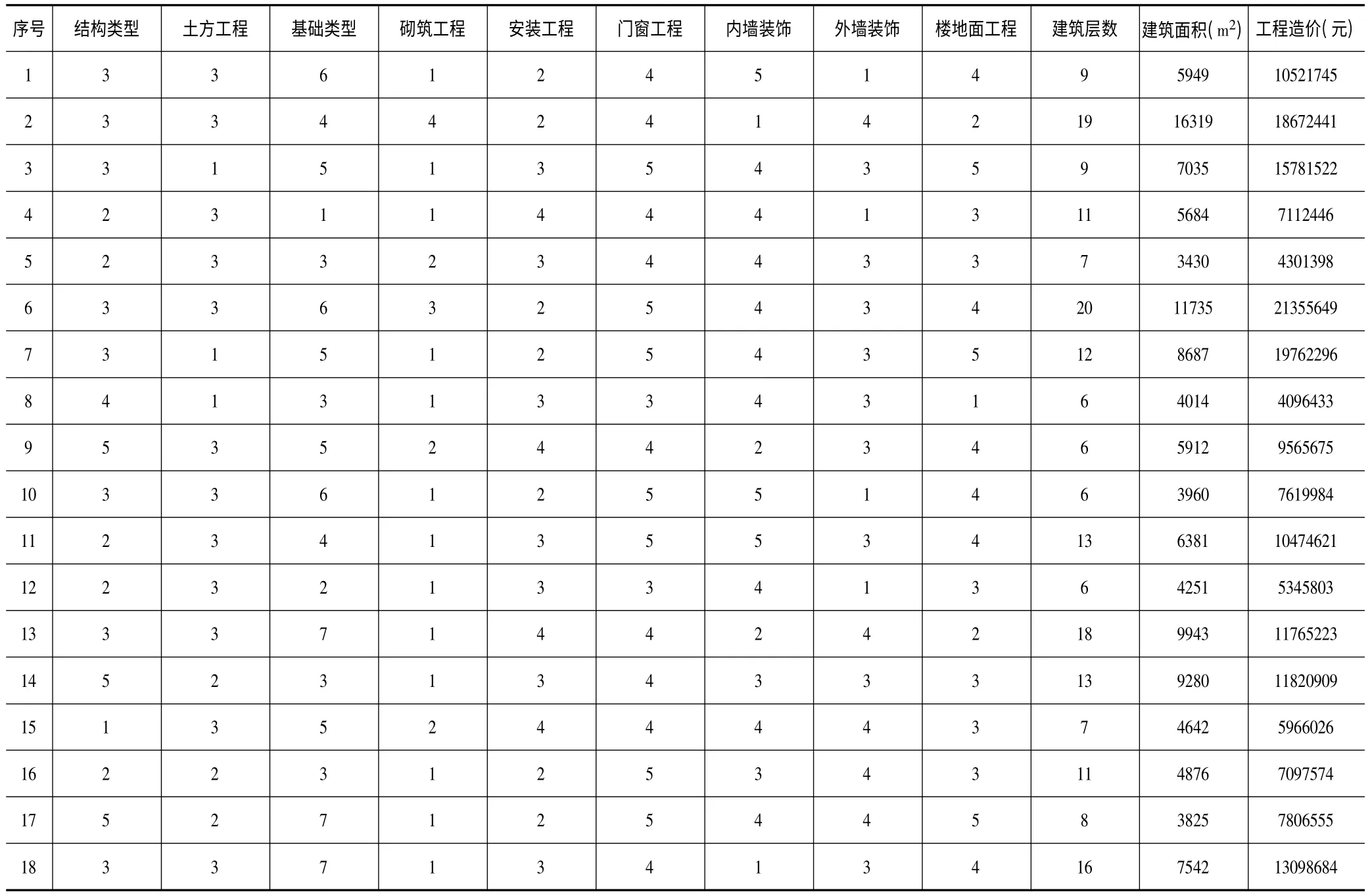
表2 定量化處理后的樣本數據

2.2 估算模型在Matlab 中的建立

2.2.1 Matlab 中BP 神經網絡模型的建立

在獲取住宅項目的樣本數據后，可以在Matlab 軟件中進行實例仿真。本文在Matlab R2012a 環境下建立BP 神經網絡，輸入的特征向量為P，結合經驗公式采用試湊法發現當隱含層單元數選取為13 時，網絡收斂速度最快，精度最高，輸出層單元數為1，傳輸函數為tansig，網絡的訓練采用Levenberg-Marquardt 算法，選取trainlm 函數，采用newff 函數建立網絡，語句為:

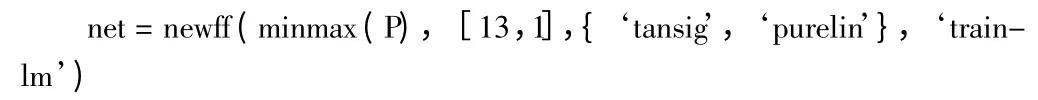
2.2.2 樣本數據的歸一化處理

在對實例樣本的數據進行定量化處理后，依然無法直接作為輸入層和輸出層變量對BP 神經網絡進行訓練，原因是表2 中的數據在數量級上相差較大，若直接用于神經網絡的訓練，會嚴重影響神經網絡的學習速度及網絡的精度、收斂情況等。

因此，在利用樣本對網絡訓練前，首先要對樣本進行歸一化處理。本文利用Matlab 中已有的premnmx 函數直接進行變量的歸一化處理，原始的輸入層特征向量為P，輸出層特征向量為T，歸一化處理后輸入為p1，輸出為t1，則premnmx 函數的調用語句為:

2.2.3 軟件中BP 神經網絡的訓練

用trainlm 函數對網絡進行訓練，用Levenberg-Marquardt 算法修正BP 神經網絡的權值和閾值，設定最大循環次數為30000，目標誤差1e-5，初始學習速率為0.02，語句為:

將表2 中前16 組樣本數據輸入網絡進行網絡訓練，訓練過程中網絡誤差的變化如圖2 所示。

圖2 訓練過程中網絡誤差變化曲線

2.3 模型仿真結果分析

將表2 中最后兩組數據輸入到已經訓練好的BP神經網絡中進行造價估算。首先將最后兩組數據進行歸一化處理，然后輸入到模型中進行估算，將計算出的數值進行反歸一化，就能得出所需的估算造價了。其中反歸一化處理可以直接調用Matlab 中的postmnmx 函數，具體的語句形式為:

將表2 最后兩組數據輸入后，得到的結果如表3 所示。

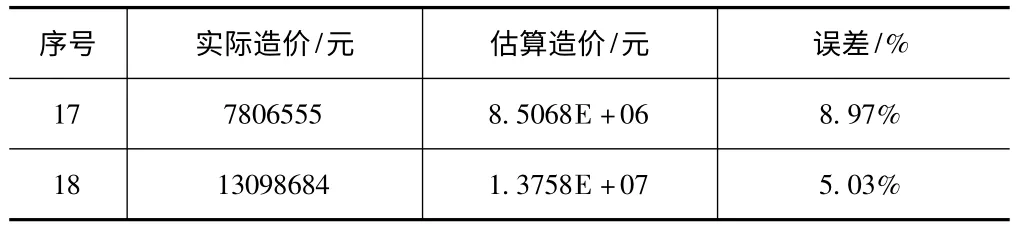
表3 工程造價估算結果

由表3 中的數據可知，本模型估算出的造價與工程的實際造價相比誤差均在10%以下，根據行業內實際工程中的經驗可知，在項目決策的最終階段，投資估算的誤差率應控制在±10%范圍內，因此，利用BP神經網絡技術建立的造價估算模型在決策階段對住宅項目的造價進行估算是可行的，是能夠滿足誤差要求的。

3 結束語

相比于傳統的造價估算方法，本文提出的基于BP 神經網絡技術的住宅項目工程造價估算模型不僅能夠滿足決策階段對于投資估算的精度要求，而且速度更快，更加適合在工程決策階段對不同方案進行比選時使用，有助于項目投資者更加快速、準確地對項目的選擇作出決策。

當然，本模型目前的估算精度依然還可以繼續提高，在未來的研究中，有需要在模型中引入更多的工程特征因素，并且完善工程特征因素的定量化處理規則，并且通過更多的實例工程數據對模型進行檢驗，以不斷完善本估價模型。

［1］馬輝.建設工程項目快速投資估算方法研究［D］.天津大學，2006.

［2］張智峰，白秀巍，艾永利.影響民用住宅造價的幾個因素［J］.福建建材，2007，05:117-118.

［3］梁文珠.影響住宅建筑工程造價的主要因素分析［J］.科協論壇(下半月)，2009，02:149.

［4］葉青，王全鳳.基于BP 神經網絡的工程估價模型及其應用［J］.廈門大學學報(自然科學版)，2008，06:828-831.

［5］嚴薇，龍昭乾，劉亮晴.基于人工神經網絡的住宅造價估算［J］.建筑經濟，2009，S1:312-315.

［6］李曉娟.基于BP 神經網絡的工程造價估算模型研究［J］.甘肅聯合大學學報(自然科學版)，2011，04:47-49 +113.

［7］王建茹.基于BP 神經網絡的建設工程造價預測方法［J］.沈陽建筑大學學報(社會科學版)，2014，01:42-45.

［8］周開利，康耀紅.神經網絡模型及其MATLAB 仿真程序設計［M］.北京:清華大學出版社，2005:69-100.