一種基于頻率校正的BPSK信號高精度載頻估計(jì)算法
易輝++侯孝民++吳濤


摘 要: 為了實(shí)現(xiàn)BPSK信號載頻的高精度估計(jì),提出一種基于頻率校正的高精度BPSK信號載頻估計(jì)算法。算法通過非線性變換將BPSK信號的載頻估計(jì)問題轉(zhuǎn)化為對點(diǎn)頻信號的估計(jì),再用DFT對點(diǎn)頻信號進(jìn)行粗估計(jì),針對DFT估計(jì)頻率分辨率差的問題,采用相位差校正法對DFT估計(jì)頻率進(jìn)行校正,從而實(shí)現(xiàn)BPSK信號載頻的高精度估計(jì)。最后,通過性能分析和計(jì)算機(jī)仿真驗(yàn)證了算法的有效性,其結(jié)果表明:該算法在低信噪比情況下能獲得較好的估計(jì)精度,在高信噪比情況下,估計(jì)精度大幅提高。
關(guān)鍵詞: BPSK信號; 載頻估計(jì); DFT; 相位差校正法
中圖分類號: TN914.2?34 文獻(xiàn)標(biāo)識碼: A 文章編號: 1004?373X(2015)22?0004?04
載頻估計(jì)是數(shù)字信號分析的重要內(nèi)容。在測控任務(wù)中,通過測量飛行器和觀測站之間的相對運(yùn)動引起的載波多普勒頻移可計(jì)算出飛行器的相對徑向速度[1?3]。同時(shí),在電子對抗中,尤其是對未知信號的偵查中,載頻估計(jì)也是信號后續(xù)處理的基礎(chǔ)[4]。因此,研究BPSK信號載頻的高精度估計(jì)有著十分重要的意義。
BPSK載頻估計(jì)的典型方法大致可分為兩類:第一類是通過現(xiàn)代譜估計(jì)的方法進(jìn)行譜估計(jì)及測頻,這類方法算法復(fù)雜,計(jì)算量大,且需要較高的信噪比;第二類是通過對信號進(jìn)行平方運(yùn)算,將BPSK信號載頻估計(jì)問題轉(zhuǎn)化為點(diǎn)頻信號頻率估計(jì)問題[5]。該方法在工程中較為常用,其載頻估計(jì)精度取決于點(diǎn)頻信號的估計(jì)精度。
對于點(diǎn)頻信號的估計(jì),常用的有時(shí)域法、頻域法、最大似然法和特征子空間法。時(shí)域法主要包括過零檢測法[6]和相位法[7],適合在信噪比比較高的情況下使用,在信噪比較低時(shí)性能急劇下降;頻域法主要包括直接法(周期圖法)、Rife算法[8]、Quinn算法[9?10]及其他基于DFT的各種改進(jìn)算法;這些方法可以用快速傅里葉算法(FFT)快速實(shí)現(xiàn),在工程上應(yīng)用廣泛。直接采用DFT法估計(jì)頻率時(shí),存在很嚴(yán)重的欄柵效應(yīng)[11],估計(jì)精度取決于頻率分辨率。而頻譜分辨率取決于采樣頻率和采樣點(diǎn)數(shù)(FFT點(diǎn)數(shù)),當(dāng)采樣頻率一定時(shí),想要獲得高精度的估計(jì)就必須不斷提高采樣點(diǎn)數(shù),這會造成運(yùn)算時(shí)間過長。
1 基于頻率校正的BPSK載頻估計(jì)算法
為了克服欄柵效應(yīng),同時(shí)兼顧運(yùn)算速度,本文提出一種基于頻率校正的BPSK信號高精度載頻估計(jì)算法。離散頻譜相位差校正法[12],利用DFT變換后譜線的相位信息對離散譜線進(jìn)行校正,可對點(diǎn)頻信號的頻率進(jìn)行高精度估計(jì)。本文將離散頻譜相位差校正法應(yīng)用到BPSK信號的載頻估計(jì)中,通過對BPSK采樣信號進(jìn)行平方運(yùn)算,得到二倍載波的單頻分量[2f0],對得到的信號進(jìn)行DFT運(yùn)算,并對頻譜進(jìn)行最大值搜索便可獲得BPSK信號二倍載頻的粗估計(jì)。在此基礎(chǔ)上,利用相位差校正法對離散頻譜進(jìn)行校正,便可得到二倍載頻[2f0]的高精度估計(jì)。為了避免在平方運(yùn)算后的頻率模糊,需要在平方運(yùn)算前進(jìn)行二倍內(nèi)插并濾除鏡像。算法的處理框圖如圖1所示。
3 頻率校正法性能分析
本文先對BPSK進(jìn)行平方運(yùn)算,將BPSK信號載頻估計(jì)轉(zhuǎn)換成電頻信號頻率估計(jì)。用DFT變換對點(diǎn)頻信號進(jìn)行粗略估計(jì),在DFT估計(jì)的基礎(chǔ)上,用相位差校正法對粗估結(jié)果進(jìn)行頻率校正。
相對于直接DFT估計(jì),頻率校正法只增加了頻率校正過程,并不會增加太多運(yùn)算量。由于增加了頻率校正過程,DFT粗估計(jì)的精度要求不需要太高,前期做DFT的點(diǎn)數(shù)也可以相對降低。假設(shè)采樣點(diǎn)數(shù)為[N2]點(diǎn),經(jīng)過內(nèi)插濾波后變?yōu)镹點(diǎn),平方運(yùn)算需要進(jìn)行N次實(shí)數(shù)乘法運(yùn)算,DFT用FFT實(shí)現(xiàn)需要[N2]log2 N次復(fù)數(shù)乘法運(yùn)算,到此便是使用直接DFT估計(jì)的運(yùn)算量;增加頻率校正過程,第二段信號可以只做第[k0]點(diǎn)的DFT而不必做N點(diǎn)的FFT,這里需要N-m次復(fù)數(shù)乘法運(yùn)算,增加的運(yùn)算量主要來自這N-m次復(fù)數(shù)乘法,這相對于[N2]log2 N來說非常的小。由于本文是在DFT估計(jì)的基礎(chǔ)上做頻率校正,對DFT的頻率分辨率要求不用太高,所用的采樣點(diǎn)不必太長,這可以減小DFT的運(yùn)算量。直接DFT估計(jì)的精度取決于DFT的頻率分辨率,即由采樣頻率和采樣點(diǎn)數(shù)決定,估計(jì)精度為頻率分辨率的一半。而相位差校正法理論上的誤差是極小的,不存在分辨率的問題。因此,在相同運(yùn)算量的情況下,相位差校正法載頻估計(jì)的精度將遠(yuǎn)遠(yuǎn)高于直接DFT估計(jì)法。
關(guān)于N和m的取值問題,N作為DFT的點(diǎn)數(shù),N越大,時(shí)間越長,頻譜越窄,旁瓣效應(yīng)就越小,但N過大會導(dǎo)致運(yùn)算時(shí)間過長,所以,N的選取要在精度和運(yùn)算速度上做一折中。為了使第二次N-m點(diǎn)做DFT的點(diǎn)數(shù)盡量長(頻譜盡量窄),m應(yīng)取較小的整數(shù)值[12]。
4 仿真結(jié)果及分析
下面對上述算法進(jìn)行仿真實(shí)現(xiàn)。仿真條件:待估計(jì)BPSK信號的載頻為59 kHz,采樣頻率300 kHz,取N=1 024的個(gè)采樣點(diǎn)。信噪比從-5~5 dB以0.25 dB的間隔變化,對每個(gè)信噪比做1 000次蒙特卡洛仿真。這里所說的信噪比是調(diào)制后信號的功率比噪聲功率。
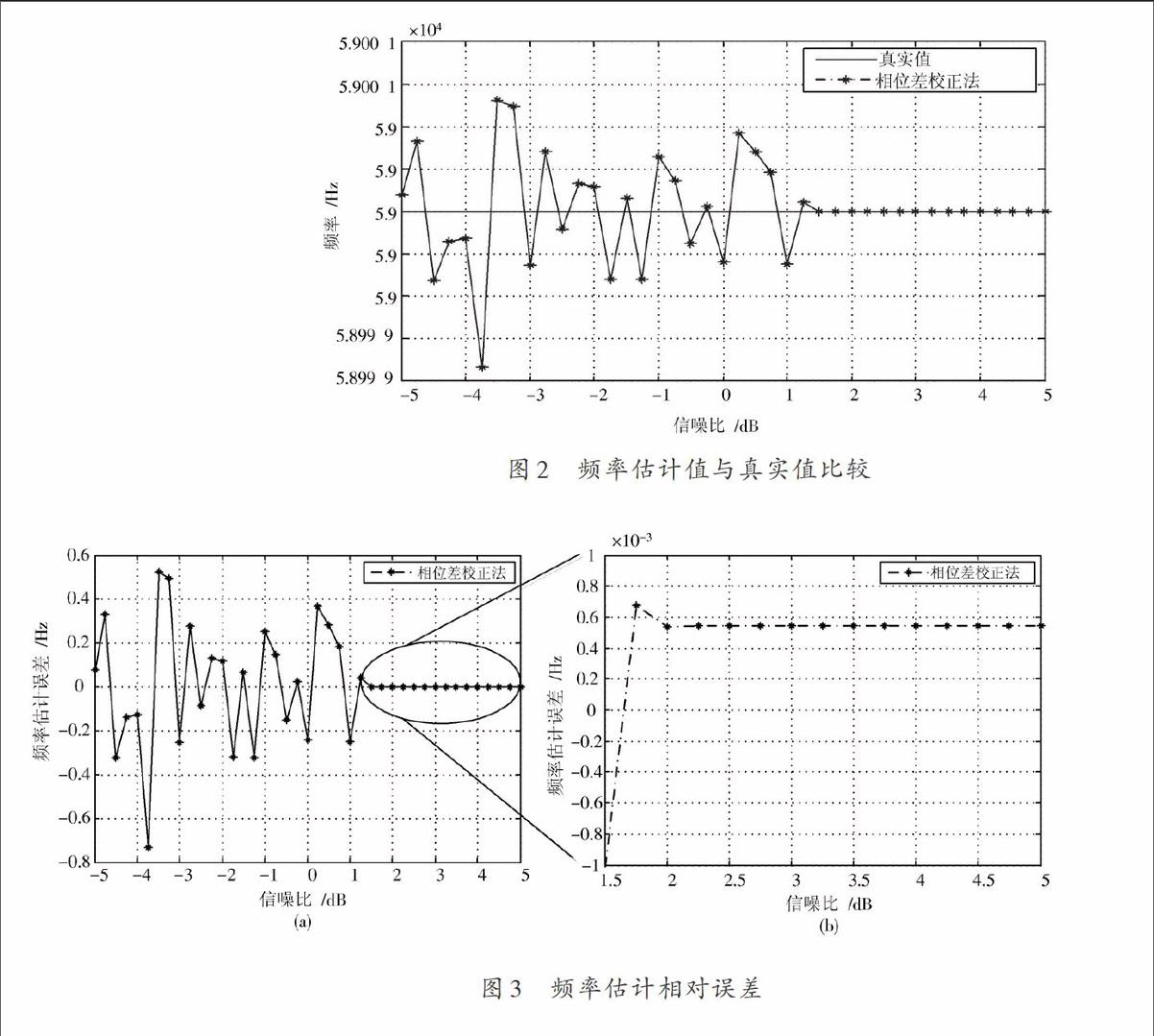
二倍內(nèi)插并濾波后,信號點(diǎn)數(shù)將變?yōu)? 048個(gè)點(diǎn),采樣率變?yōu)?00 kHz。如果只用FFT估計(jì)載頻的話,此時(shí)頻譜的頻率分辨率為[Δf=0.293 kHz],估計(jì)的精度為頻率分辨率的一半,即[0.146 kHz]。若在FFT估計(jì)后,再做頻率校正,估計(jì)精度將大大提高。1 000次蒙特卡洛仿真結(jié)果如圖2,圖3所示。
圖2所示為載波頻率估計(jì)值與真實(shí)值對比圖。從圖2中可以看出,當(dāng)信噪比低于1 dB的時(shí)候,載頻估計(jì)值在真實(shí)值附近上下大幅度波動。這是由于噪聲過大,影響了相位差的計(jì)算結(jié)果,導(dǎo)致校正后,估計(jì)頻率呈現(xiàn)出隨機(jī)波動的現(xiàn)象。當(dāng)信噪比高于1 dB時(shí),估計(jì)頻率逐漸穩(wěn)定并趨近于真實(shí)值,在2 dB附近達(dá)到穩(wěn)定狀態(tài)。當(dāng)信噪比高于2 dB時(shí),載頻估計(jì)值基本等于真實(shí)值。
圖3所示為載頻估計(jì)值減去真實(shí)值后得到的誤差。從圖3中可以看出,當(dāng)信噪比低于1 dB時(shí),估計(jì)誤差較大且波動較為劇烈,但仍然遠(yuǎn)小于DFT的頻率分辨率,估計(jì)誤差在1 Hz以內(nèi)。可以算出相對誤差可達(dá)到[10-5]數(shù)量級。當(dāng)信噪比高于2 dB時(shí),估計(jì)誤差在0.001 Hz以內(nèi),相對誤差可達(dá)[10-8]數(shù)量級。
從圖3中的放大圖中還可以看出,當(dāng)信噪比大于2.5 dB以后,頻率估計(jì)的誤差并沒有再減小,而是一個(gè)穩(wěn)定的值,這正是由于前面所分析的[XsN(ejω)]正、負(fù)頻譜相互疊加所造成的。
5 結(jié) 語
本文將相位差校正法應(yīng)用到BPSK信號的載頻估計(jì)中,對算法原理進(jìn)行推導(dǎo)并分析了算法的性能,通過仿真分析驗(yàn)證了算法的估計(jì)精度和有效性。基于頻率校正的BPSK信號載頻估計(jì)算法是針對DFT的頻率估計(jì)的校正算法,具有速度快、實(shí)時(shí)性好的優(yōu)點(diǎn),有利于硬件實(shí)現(xiàn)。同時(shí),該算法運(yùn)算簡單,估計(jì)精度高,可以有效克服欄柵效應(yīng),適用飛行器測控。
參考文獻(xiàn)
[1] 劉嘉興.飛行器測控與信息傳輸技術(shù)[M].北京:國防工業(yè)出版社,2011.
[2] 黃富彪,何兵哲.一種衛(wèi)星信號載波頻率精確估計(jì)算法[J].現(xiàn)代電子技術(shù),2012,35(3):129?131.
[3] 劉嘉興.飛行器測控通信工程[M].北京:國防工業(yè)出版社, 2010.
[4] Richards Mark A.雷達(dá)信號處理基礎(chǔ)[M].北京:電子工業(yè)出版社,2012.
[5] 鄭紀(jì)民,胡亞.一種MPSK信號載頻高精度實(shí)時(shí)估計(jì)算法[J].無線電工程,2012(5):21?23.
[6] 張旻,王倫文,陳家松.用于通信對抗偵察的高精度測頻方法[J].無線電通信技術(shù),2000(5):48?50.
[7] BOASHASH B. Estimating and interpreting the instantaneous frequency of a signal II: Algorithms and application [J]. Proceedings of the IEEE, 1992, 80(4): 540?568.
[8] RIFE D R B. Single tone parameter estimation from discrete?time observations [J]. IEEE Transactions on Information Theory, 1974, 20(5): 591?598.
[9] QUINN B G. Estimation of frequency, amplitude, and phase from the DFT of a time series [J]. IEEE Transactions on Signal Processing, 1997, 45(3): 814?817.
[10] 謝勝,陳航,于平,等.基于Quinn算法和相位差法的正弦波頻率估計(jì)綜合算法[J].信號處理,2011(5):771?775.
[11] 陳奎孚,焦群英,高小榕.提高 FFT 譜質(zhì)量的一種新方法[J].振動·測試與診斷,1998(3):62?66.
[12] 朱利民,賈民平,鐘秉林.轉(zhuǎn)子振動監(jiān)測中的采樣與相位誤差補(bǔ)償[J].東南大學(xué)學(xué)報(bào),1997(2):117?122.

