非線性特性在船舶電力系統(tǒng)中的研究及仿真

王 超，王 剛

(沈陽工程學(xué)院，遼寧 沈陽110136)

0 引 言

船舶電力系統(tǒng)的穩(wěn)定性是指在航行過程中系統(tǒng)受到干擾(如絕緣故障﹑系統(tǒng)負(fù)載瞬間突變以及海水乳濁等)時，系統(tǒng)各支路發(fā)電機(jī)是否能夠在一定范圍內(nèi)保持同步，并提供穩(wěn)定頻率的電壓。由于現(xiàn)代船舶電力系統(tǒng)結(jié)構(gòu)越來越復(fù)雜，負(fù)載分支也越來越多，導(dǎo)致船舶供電穩(wěn)定性更加重要。

船舶電力系統(tǒng)屬于一類非線性控制系統(tǒng)，同時隨著現(xiàn)代控制理論的發(fā)展，系統(tǒng)的自動化程度不斷提升，與傳統(tǒng)的機(jī)械發(fā)電不同，現(xiàn)在大部分已采用自動化發(fā)電方式，這就對電力系統(tǒng)的穩(wěn)定性提出更高要求。

本文首先研究了系統(tǒng)支路負(fù)載與發(fā)電機(jī)組的非線性特性，基于魯棒性控制原理，建立了非線性數(shù)學(xué)模型，反映了整個支路負(fù)載與發(fā)電系統(tǒng)耦合特性以及負(fù)載動靜態(tài)過程。

最后，本文提出了一種利用Hamilton 函數(shù)方式的并聯(lián)電力非線性控制系統(tǒng)，通過預(yù)置系統(tǒng)狀態(tài)以及運(yùn)行狀態(tài)反饋系統(tǒng)非線性特征系數(shù)來調(diào)節(jié)系統(tǒng)的連續(xù)性及穩(wěn)定性，并通過仿真驗(yàn)證了系統(tǒng)的有效性。

1 船舶電力系統(tǒng)的非線性原理

1.1 電力系統(tǒng)非線性特性

一般船舶電力系統(tǒng)主要由變電器﹑連接電纜﹑發(fā)電源機(jī)組﹑中央控制器以及配電裝置組成，是一個異構(gòu)復(fù)雜的非線性結(jié)構(gòu)。而電路中每個元器件特性各不相同，對元器件的單獨(dú)分析是不現(xiàn)實(shí)的，所以對整個系統(tǒng)的非線性以及造成供電系統(tǒng)不穩(wěn)定的主要元器件進(jìn)行分析成為主流。

現(xiàn)在，根據(jù)船舶電力系統(tǒng)不同的負(fù)載模型，對系統(tǒng)的非線性數(shù)學(xué)模型主要有以下3 種:網(wǎng)絡(luò)降階模型﹑普通簡化模型﹑網(wǎng)絡(luò)保留結(jié)構(gòu)。本文主要對網(wǎng)絡(luò)降階模型進(jìn)行研究。

假設(shè)在穩(wěn)態(tài)過程中，發(fā)電機(jī)組的輸出功率保持不變，電力系統(tǒng)負(fù)載可用接入中性點(diǎn)的相同阻抗來代替，n 臺發(fā)電器組可以等效為帶有n個電源節(jié)點(diǎn)的網(wǎng)絡(luò)，因此n 臺發(fā)電器組構(gòu)成的電力系統(tǒng)的數(shù)學(xué)模型可以用一個2n 階的非線性偏微分方式來表示，如圖1 表示為n 組多電機(jī)系統(tǒng)的網(wǎng)絡(luò)結(jié)構(gòu)圖，圖2為其數(shù)學(xué)模型。

圖1 多發(fā)電機(jī)組電力系統(tǒng)Fig.1 Multi generator power system

圖2 電力系統(tǒng)數(shù)學(xué)模型Fig.2 The mathematics model of power system

整個系統(tǒng)將負(fù)載節(jié)點(diǎn)、發(fā)電機(jī)內(nèi)部電路、發(fā)電機(jī)端口電路進(jìn)行整體建模，圖2 中f(?，V)函數(shù)為非線性，且在各種狀態(tài)下滿足二階擺動方程f(?，V)=。通過對網(wǎng)絡(luò)結(jié)構(gòu)的數(shù)學(xué)模型分析可以得到影響系統(tǒng)穩(wěn)定的關(guān)鍵元器件動態(tài)特性。

1.2 船舶電力系統(tǒng)的非線性控制

現(xiàn)代船舶電力系統(tǒng)對于非線性控制一般有以下2 種方式:

1)將相同型號發(fā)電機(jī)組構(gòu)成的電力系統(tǒng)近似線性化，依據(jù)H∞線性控制理論，采用自動化控制技術(shù)與PID控制相結(jié)合來控制發(fā)電機(jī)在負(fù)荷變化條件下的電壓幅值及頻率穩(wěn)定性。

2)采用理想建模方法精確描述電力柴油機(jī)轉(zhuǎn)速與供電電壓之間的相互關(guān)系，建立船舶電力柴油機(jī)的非線性模型，同時將非線性模型等化為H∞線性控制、勵磁控制及反饋系統(tǒng)控制器共同控制供電系統(tǒng)的穩(wěn)定性。圖3 給出了此種方式的船舶電力系統(tǒng)非線性控制結(jié)構(gòu)。

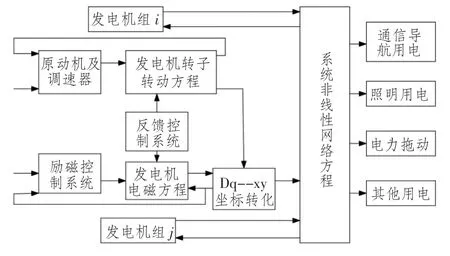
圖3 船舶電力系統(tǒng)的控制結(jié)構(gòu)圖Fig.3 The control structure diagram of ship power system

2 動態(tài)負(fù)載船舶電力系統(tǒng)數(shù)學(xué)模型

2.1 柴油發(fā)電機(jī)組的同步輸出功率

將圖1 中發(fā)電機(jī)端口電路電壓U 分為d，q 方向的2個分量，表達(dá)式如下:

現(xiàn)實(shí)中各電網(wǎng)供電系統(tǒng)之間距離較短，傳輸電纜的電壓幅值及頻率較低，傳輸電纜阻抗及變頻器阻抗可近似為零，則發(fā)電機(jī)電流如下:

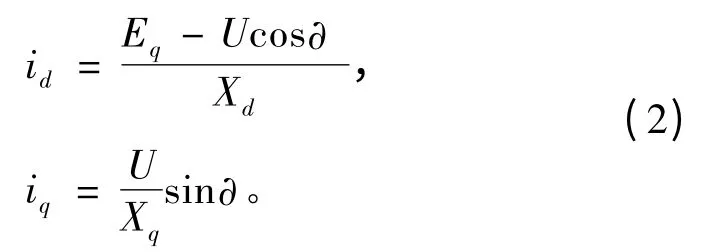
其中Eq為不加負(fù)載時發(fā)電機(jī)電勢。

系統(tǒng)穩(wěn)態(tài)時的電勢E′q與Eq之間的聯(lián)系為:

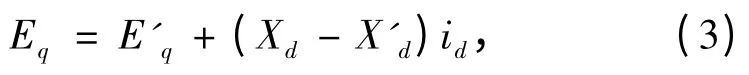
船舶三相發(fā)電機(jī)組的輸出功率為:

同時由于船舶電力系統(tǒng)發(fā)電機(jī)組都是同步發(fā)電，Xd≠Xd，將式(2)中的id，iq代入式(4)，可得到有功功率輸出方程:

柴油發(fā)電機(jī)功率角度?與其電轉(zhuǎn)速ω 之間有如下關(guān)系:

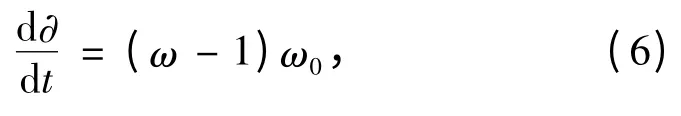
其中ω0為穩(wěn)態(tài)時的初始轉(zhuǎn)速。將式(6)代入式(5)并結(jié)合算式(2)和式(3)，即可得到柴油發(fā)電機(jī)組非穩(wěn)態(tài)下的非線程數(shù)學(xué)方程:

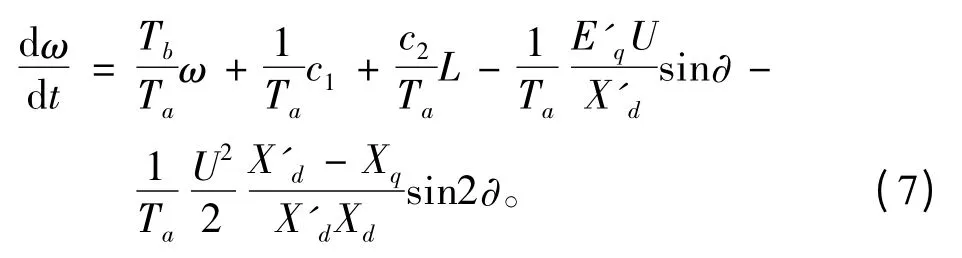
2.2 柴油發(fā)電機(jī)組分散勵磁系統(tǒng)描述

船舶電力結(jié)構(gòu)中的勵磁控制器在整個非線性系統(tǒng)中的位置如圖1所示，現(xiàn)在對其一般采用三階數(shù)學(xué)模型分析，并且假設(shè)發(fā)電機(jī)電子轉(zhuǎn)速恒定，且忽略非穩(wěn)態(tài)的凸極情況，則勵磁控制器暫態(tài)方程如下:

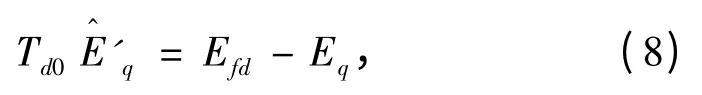
將式(7)代入此方程得到其動態(tài)方程:

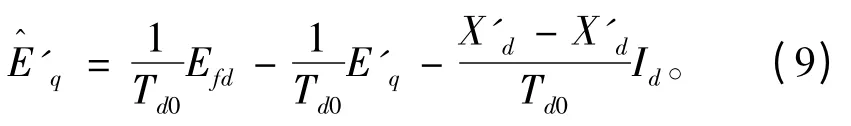
聯(lián)系式(8)和式(9)，可得到分散勵磁控制系統(tǒng)的三階數(shù)學(xué)方程如下:

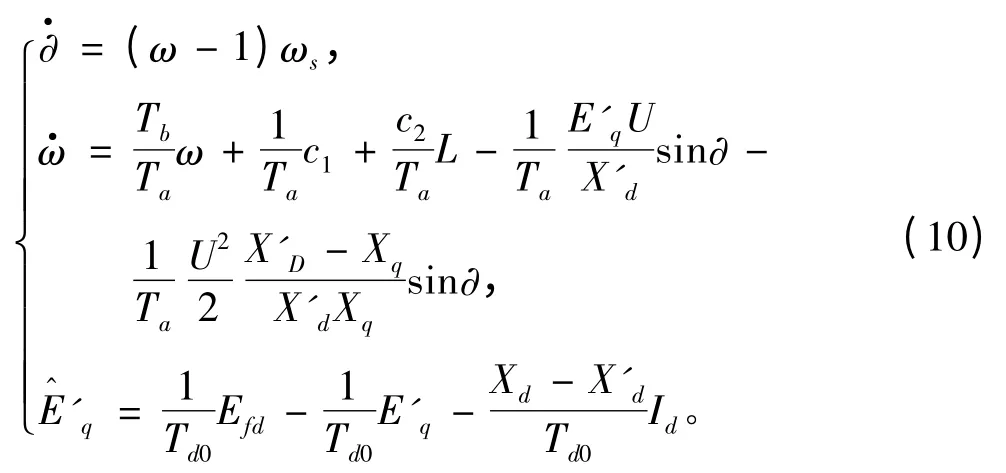
2.3 船舶電力系統(tǒng)的動態(tài)負(fù)載描述

現(xiàn)在船舶由于其容量越來越大，電路系統(tǒng)的負(fù)載容量也越加龐大，負(fù)載主要由永磁同步電機(jī)及螺旋設(shè)備組成。

永磁同步電機(jī)同樣采用d－q 坐標(biāo)描述，理想狀態(tài)下有如下假設(shè):

1)永磁電機(jī)磁路消耗忽略，并且電機(jī)沒有強(qiáng)阻尼干擾。

2)三相電機(jī)的電壓及電流相等。

3)永磁電機(jī)的磁體不會衰變。

則它在d－q 坐標(biāo)下的電壓方程如下:

式中rS為定子電阻;np為極對數(shù);ωr為發(fā)電轉(zhuǎn)子轉(zhuǎn)速;φd和φq為磁體的坐標(biāo)分量。

船舶動力系統(tǒng)的負(fù)載可用如下方程表示:

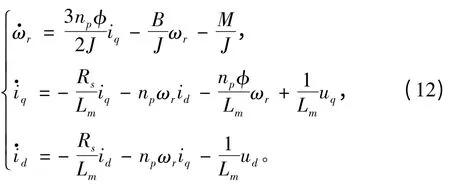
式中Lm為d－q 坐標(biāo)下勵磁電感;φ 為永磁體產(chǎn)生的磁場;M 為負(fù)載轉(zhuǎn)矩;J 為轉(zhuǎn)子定量;B 為系統(tǒng)阻尼大小。

3 Hamilton 方法控制系統(tǒng)及仿真

3.1 Hamilton 方法非線性控制描述

船舶電站的非線性控制系統(tǒng)結(jié)構(gòu)如圖4所示。

圖4 是基于Hamilton 函數(shù)非線性控制思想，整個控制系統(tǒng)采用先分后合，分為暫態(tài)穩(wěn)定以及動態(tài)系統(tǒng)，同時采用Hamilton 方法設(shè)計控制器使得系統(tǒng)中影響供電穩(wěn)定的主要器件保持恒定，提高系統(tǒng)的暫態(tài)穩(wěn)定性，算法如下:

1)Hamilton 函數(shù)輸入(u，y)為一階輸出，則整個控制系統(tǒng)穩(wěn)態(tài)子狀態(tài)方程如下:

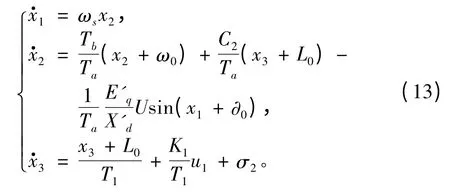
式(13)為控制器輸出的電壓u1的零暫態(tài)方程。

2)設(shè)計控制器的電壓u1使得上式中內(nèi)部保持恒定，同時需要設(shè)計勵磁控制器u2，使整個船舶電力非線性控制系統(tǒng)達(dá)到動態(tài)平衡。根據(jù)魯棒理論，系統(tǒng)平衡的評價如下式:

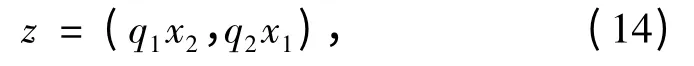
上式q1和q2為權(quán)重因子，用來調(diào)節(jié)輸出電壓穩(wěn)定。

3)令x1=e1，取得虛函數(shù)=-ce1，同時V1，可得下式:

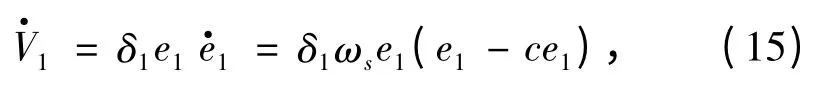
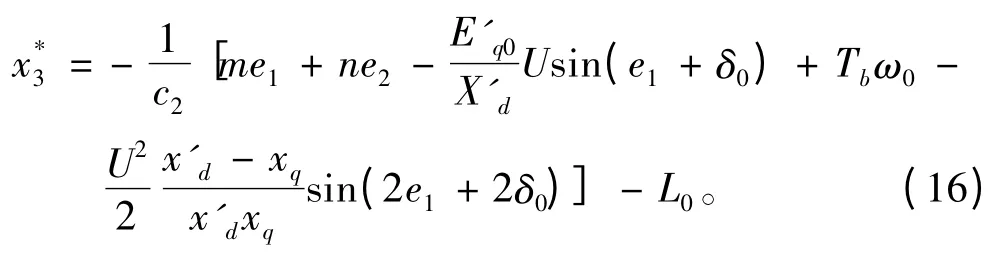
5)最后取得基于Hamilton 函數(shù)方法的控制器u 公式:

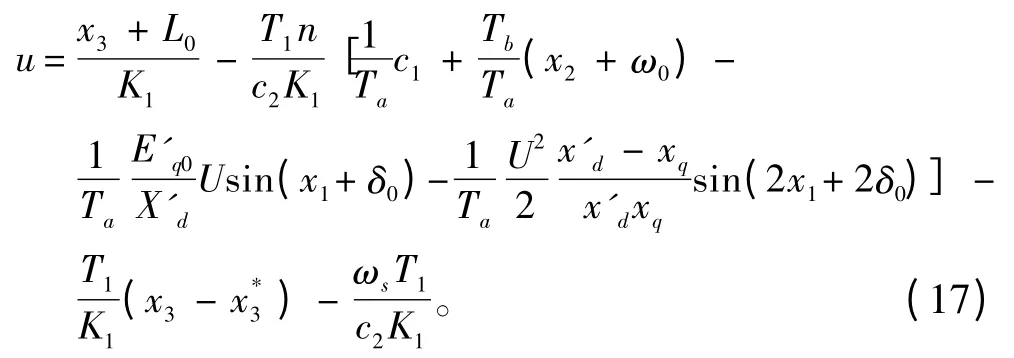
3.2 算法仿真

船舶柴油發(fā)電的功率值為1 250 kW，機(jī)組轉(zhuǎn)速為n=1 500 r/min，額定傳輸距離為11.9 kN·m，同步發(fā)電機(jī)組三相電壓390 V，電流為2 310 A，因子系數(shù)為0.8，勵磁控制系統(tǒng)電壓83 V，電流為7.7 A，各參數(shù)如表1～表4所示。

表1 發(fā)電機(jī)參數(shù)Tab.1 Parameters of generator

表2 系統(tǒng)參數(shù)Tab.2 System parameters

表3 負(fù)載電子器件參數(shù)Tab.3 Parameters of electron device

表4 非線性控制參數(shù)Tab.4 Nonlinear control parameters

圖5 給出了仿非線性控制方法的負(fù)載功率仿真曲線。

通過圖5 可以看到，控制系統(tǒng)隨著時間的推移不斷的改善了發(fā)電機(jī)輸出電壓的品質(zhì)，該控制系統(tǒng)在船舶電力系統(tǒng)中具有較強(qiáng)的動態(tài)穩(wěn)定性。

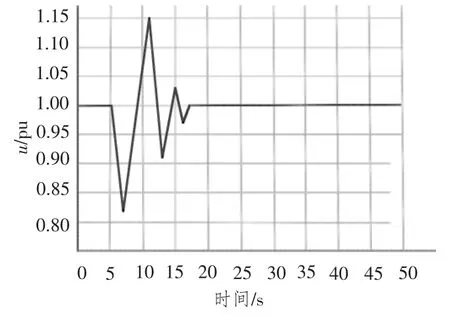
圖5 仿真曲線圖Fig.5 The curve of simulation result

4 結(jié) 語

本文首先研究了現(xiàn)代船舶電力系統(tǒng)的非線性原理及特性，隨后詳細(xì)描述了動態(tài)負(fù)載非線性數(shù)學(xué)模型，以及支路負(fù)載與系統(tǒng)非線性的耦合，同時給出了柴油發(fā)電機(jī)分散勵磁控制系統(tǒng)描述。

最后本文給出了一種基于Hamilton 函數(shù)方法的船舶非線性電力控制系統(tǒng)，詳細(xì)了描述了此方式算法步驟，并通過仿真證明了該方法的有效性。

［1］ZHAO Jie-mei，MENG Jie，ZHANG Li-jun.Passivity-based sliding mode predictive control of discrete-time singular systems with time-varying delay［C］//IEME 2011.

［2］ISHIMARU M，YOKOYAMA R，SHIRAI G，et al.Robust thyristor-controlled series capacitor controller design based on linearmatrix inequality for a multi－machine power system［J］.Electrical Power Energy Systems，2002，24:621－629.

［3］都紹裘.非線性波阻及船型優(yōu)化研究［J］.艦船科學(xué)技術(shù)，1994(6):1－5.

［4］張冰，姜長生.艦船在水平面運(yùn)動中非線性模型的建立［J］.艦船科學(xué)技術(shù)，2005(5):25－27.

［5］ESEOBAR G，SIRAR H.A Passivity based-sliding mode control approach for the regulation of power faector precompensators［J］.Decision and control，1998(3):2423－2424.

［6］錢佳，何祖軍.船舶動力定位非線性自適應(yīng)濾波算法［J］.艦船科學(xué)技術(shù)，2013(12):25－28.

［7］JASWANTH C，RANJITH M，ASAD Davari Edge detection and segmentation formachine vision［C］//IEEE，2005:457－461.