基于GA+ACO的交通擁擠及事故規避系統研究

陸文昌++鄧傲++袁朝春++陳龍

摘 要：為了減少車輛在行駛過程中產生的交通事故和規避擁擠道路，研究了道路擁擠程度的影響因素和評價指標以及道路事故的理論與模型。提出采用路網的動態路阻對事故的影響程度和道路擁擠程度進行綜合評價，并對動態路阻采用模糊理論進行量化。同時研究了遺傳算法和蟻群算法在該規避系統中的應用，采用遺傳蟻群的混合算法，綜合了遺傳算法全局搜索和蟻群算法求解精確的特點。用Matlab對該路阻函數和混合算法進行仿真，并進行了實際路網測試，結果表明利用該路阻函數和混合算法能夠達到規避擁擠、規避潛在事故和規避已發事故的目的。

關鍵詞：交通路網；遺傳蟻群混合算法；道路擁擠；最優路徑；事故阻斷

中圖分類號：U461.91文獻標文獻標識碼：A文獻標DOI：10.3969/j.issn.2095-1469.2015.05.10

隨著社會經濟的飛速發展，我國的汽車保有量也逐年提高，造成道路交通承載壓力越來越大，導致大量的交通擁擠和交通事故。所以道路交通的擁擠程度評價和交通事故的預測規避對交通規劃以及道路交通安全控制等具有重要意義。交通擁擠程度評價系統的核心在于動態路阻的計算和最小擁擠路徑的求解。國內外對于交通擁擠進行了多方面的研究，在動態路阻的計算與評價方面主要有層次分析法、模糊綜合法、主成分分析法等[1]。最小擁擠路徑的求解算法經典的有Dijkstra、Floyd、A*算法以及它們相應的改進算法等[2]。仿生智能路徑優化算法是針對實際路網的復雜性以及用傳統方法求解優化問題存在很多困難的情況而發展起來的。目前國內外研究熱門的智能路徑優化算法主要有遺傳算法、粒子群優化算法以及蟻群算法等[3]。

交通事故的預測是道路安全評價、規劃以及決策的基礎，其預測模型主要有回歸模型法、經驗模型法、時間序列法等[4]。國內外大多數論文一般將擁擠評價和事故預測規避分開，然而兩者間互相有很深的聯系，事故的發生會導致擁擠程度的快速增長，擁擠程度也會導致潛在事故概率的變化。考慮到道路交通各影響因素內部關系的錯綜復雜性和價值系統的模糊性，對模糊理論進行了相關研究，利用模糊綜合法設計了一種路阻的動態計算模型。將道路的擁擠情況和事故鏈結合綜合評價，然后利用遺傳與蟻群混合算法，綜合遺傳算法的全局搜索能力和蟻群算法的快速精確性，進而求解得到最優路徑，達到規避擁擠、規避潛在事故和規避已發事故的目的。

1 路網的數學模型

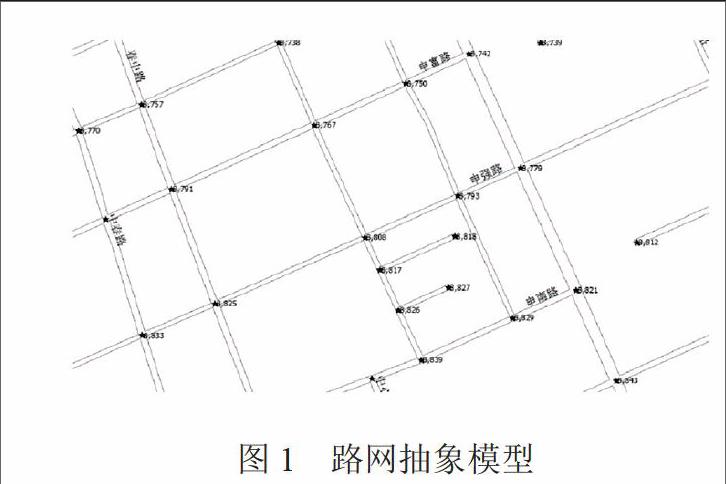
為了迅速、準確而安全地到達目的地，車輛行駛過程中，就要有效地避開擁擠路段和潛在風險事故大的路段或已發生事故的路段，即在起點與終點間尋找一條綜合了道路擁擠與事故概率后的最優路徑。為了解決上述問題，以結構直觀的交通網路圖（圖1

為用Mapbasic語言編程后，得到的路網抽象模型）為基礎，將最優路徑的尋找轉換成在有向賦權圖上求解兩點間最短距離的問題。這里的有向賦權圖是這樣來建立的，即用道路的交叉口或者道路特性（道路寬度、等級）發生改變的位置對應圖的節點，兩交叉口之間的路段對應圖中的邊，路段的長度作為該邊的權值。這樣的賦權有向圖用下述公式表示為

。

式中，G為表示路網的賦權有向圖；

為路網節點集合；n為路網節點數；E為路網邊集合；m為路網邊數；D為路網的路權矩陣；dij為i、j兩節點間的道路長度，m。根據不同的優化目標，可以定義相應的路權，反映到賦權有向圖上，就是各條邊的權。本文將其它的影響因素量化為道路的長度，即選取行駛距離為優化目標。設D（t）為路網的動態路阻矩陣，則t時刻相鄰2節點i到j的路阻可以簡單地表示為Dij（t）=λdij。

2 動態路阻的計算

2.1 動態路阻影響因數的選取

路阻影響因數主要包含兩大類：道路屬性（寬度、道路等級、交通限制）和交通參數（交通流量、速度、道路占有率、路口排隊長度等）。各個因數的影響大小不一樣，數據的獲得也存在著難易程度上的差別。高速公路或者城市快速路具有典型的連續交通流特征，在上面行駛的車輛可以在相當長的路段上不受其它道路交通流的影響而連續運行，且不會發生因紅綠燈而引起的交通擁擠現象。行駛于城市快速路和高速路上的車輛所形成的交通擁擠除了環境因素外，往往是因交通流量過大而造成的。

所以對于高速公路或者城市快速路，選取平均行程速度和交通流量[3，5]。對城市道路而言，其具有典型的間斷交通流特征，選取平均行程速度、飽和度S=V/C、平均延誤時間[3，6-7]。其中V為進口車道實際交通量，輛/h；C為進口車道通行能力，輛/h。

2.2 動態路阻選取因數的量化[3]

動態路阻矩陣Dij（t）=λdij 。

式中，。

其中λ1為道路屬性信息相關的路權系數；λ2為實時交通信息相關的路權系數；λ3為與駕駛者特殊要求相關的路權系數；λ4為與安全相關的路權系數；1為道路長度系數。

（1）λ1取值

λ1=1/GW。G為道路等級，我國將道路分為四個等級：1， 2， 3， 4，數字越大道路越差；W為道路寬度，m。

（2）λ2取值

λ1是動態路阻模型的核心之一，用于表征實時交通信息對擁擠程度的影響，其取值范圍為0～1，與相對應道路的擁擠程度成正比關系。λ2的獲取步驟如下：

①根據交通流的特性分類，即分成連續交通流和間斷交通流。

②根據不同的交通流參考國內外的評價標準，對連續交通流和間斷交通流進行擁擠程度的評價。

③利用模糊理論將評價的擁擠程度量化成0～1間可計算的數值。

對高速公路和城市快速路，影響因數為平均行程速度和交通流量。以下各表是由我國采用的《城市交通管理評價指標體系》，我國交通發展研究中心的《交通擁堵評價研究報告》和相關理論研究[7-8]制定。

模糊控制量化步驟：

①選擇模糊控制變量，具體見2.1節。

②對輸入輸出變量的模糊分割。

③選擇合適的隸屬度函數，所選擇的隸屬度函數為梯形隸屬度函數，其具有計算簡單、使用方便的特點。

④根據相關資料和經驗確定控制規則。

⑤獲取輸出曲面。

對連續交通流按照上述步驟獲取的輸出曲面如圖2所示。

城市道路屬于間斷交通流，選取的參數為飽和度、平均行程速度和平均延誤時間。

同理，利用模糊控制的步驟可得當橫坐標為平均行程速度，縱坐標為平均延誤時間時的輸出曲面，如圖3所示。

（3）λ3取值

取值為0和0.5，當高速優先時，對高速公路路阻取0，普通道路取0.5，反之分別取0.5和0。駕駛若無特殊要求取值都為0。

（4）λ4取值

事故評價同λ2，分為連續交通流和間斷交通流。對連續交通流，由鎮江市歷年交通事故分析和相關文獻[3，9]選取平均行程速度、行車間距、交通流量和貨車超載比例。對間斷交通流選取平均行程速度、行車間距、交通流量和信號交叉口違規概率。

連續交通流λ4，隸屬度函數采用高斯函數，利用重心法反模糊化，輸出曲面如圖4所示。同理，間斷交通流輸出曲面如圖5所示。

然后我們可以根據實時接收到的車速、流量等數據得到某時刻的λ2、λ4值。

（5）β的取值

令β[β1， β2， β3]，則β為權向量。采用AHP法確定其權重。構造判斷矩陣為，則A的最大特征根為3.009 2，檢驗指標RI0.009 2/0.580.016<0.1，且β（0.16， 0.30， 0.54）。故可以加權實時的λ值，進而得到實時的動態路阻矩陣。特殊地，當λ21時（表示某段道路因發生事故或其它情況完全堵塞）或當λ41時（表示某段道路非常危險，有很大概率發生交通事故），此時β2或β3取無窮（具體取999 999代替）。

3 最優路徑的計算

遺傳算法在搜索初期具有較高的向最優解收斂的速度，但之后求最優解的速率顯著下降。而蟻群算法在搜索的初期由于缺乏信息素，搜索速度緩慢，但當信息素積累到一定強度之后，向最優解收斂的速度就會迅速提高[10-11]。綜合兩種算法的特點，采用遺傳-蟻群混合算法對最優路徑進行計算。

3.1 遺傳算法與蟻群算法的融合

本文遺傳算法與蟻群算法的融合主要體現在兩個方面，一是算法初期利用遺傳算法的特點快速計算出多組優化解，然后蟻群算法根據這些優化解生成初始的信息素分布，從而彌補蟻群算法初期搜索速度緩慢的不足；二是在利用蟻群算法求解時，為了避免算法過早地陷入局部最優解同時增加求解準確率，利用遺傳操作作用于螞蟻的解分布，增加種群搜索的多樣性，從而較高概率地搜索獲得問題最優解。其算法流程圖如圖6所示。

3.2 遺傳算法生成信息素的初始分布

3.2.1 編碼

本文采用的方式為符號編碼，即用實數編號表示節點，然后用這些編號作為一種編碼形式參與遺傳操作，該編碼方法不僅易于遺傳操作，而且可以簡化優化程序，并可以保證搜索到全局最優解可能存在的整個空間[7]。

3.2.2 種群

種群包含種群的規模和產生初始種群的方法。本文初始種群采用完全隨機的方式，即先隨機產生染色體。染色體的第一個基因就是起點，第二個基因是從與起點連接的其它節點中隨機選擇的，重復進行這個過程，直到到達終點為止。為了避免產生環路，規定在一條染色體中，當一個基因被選中之后，就給該基因（節點）作個標記，只有沒有標記的基因才能被該染色體選中，該條染色體產生完成后標記全部刷新，然后重復第一步，直到產生的染色體數達到初始種群規模的要求（種群規模選擇為100）。

3.2.3 遺傳操作

（1）選擇算子：遺傳算法通過選擇操作從當前種群中選出優良個體遺傳到下一代，體現“優勝劣汰”的原則。目前常用的選擇方法有排序選擇法、分級選擇法和賭盤選擇法等。本文選擇賭盤選擇法，即每個染色體被選中的概率與其適應度值的大小成正比。此處適應度函數為fij（t）1/Dij（t）。與此同時為了解決賭盤選擇法容易引起的“早熟”和“收斂停滯”問題，采用最優保存策略，即當前種群中適應度值最大的染色體直接復制進入下一代種群，不對其進行選擇、交叉和變異操作。該策略可以加快收斂速度。

（2）交叉算子模仿了自然界有性繁殖的基因重組過程，是遺傳算法較其它進化算法的獨有特征，主要通過將兩個父代個體的部分基因相互替代得到兩個新個體。在遺傳算法中，交叉算子是產生新個體的主要手段，保證了種群的多樣性。本文采取的交叉方法為隨機單點交叉。

（3）變異算子是模仿生物由于各種偶然因素引起的基因突變，是遺傳算法中產生新個體的輔助方法，可以保持種群的多樣性，防止算法陷入局部最優解。變異算子和交叉算子相互配合，共同完成搜索最優解的過程。變異有刪除、替代、插入三種方式，由于本文遺傳算法主要工作是提供初始的信息素分布，為了節約算法的時間，采用刪除和替代兩種方式。

3.3 蟻群算法求解最優路徑

算法步驟：

（1）參數初始化。將螞蟻的位置隨機分布在節點上，根據遺傳算法產生的優化解對節點間的信息素進行分布。

（2）開始循環。對每個螞蟻，根據概率轉移公式由節點i轉移到節點j。當i，j都不在禁忌表時概率轉移公式為

。

否則為0。為啟發函數，取表達式為1/Dij（t）。α是概率轉移公式中信息素影響因子，反映了在運動過程中信息素對蟻群擇優的作用大小，其值越大蟻群越傾向于已選擇的路徑，從而易于陷入停滯狀態。β則是概率轉移公式中的啟發式影響因子，體現了算法中蟻群不同于真實蟻群所添加的啟發信息的影響大小。

（3）信息素更新，更新公式為

。

式中，。

（0<<1）表示信息素揮發系數，當第k只螞蟻在本循環中經過i，j時：

。

否則為0。Lk表示第 k只螞蟻在本次循環中所走過的路徑總長度。

（4）得到本次循環的最優路徑和次優路徑，并且路徑間進行交叉和變異操作。

（5）判斷是否達到迭代終止條件，此處選為到達一定的迭代次數。

4 仿真分析

4.1 遺傳算法對最優路徑的計算

采用Matlab對遺傳算法進行仿真。

路網圖為34個節點的賦權有向圖，如圖7所示。

用Matlab對遺傳算法進行30次仿真。選取種群規模100，交叉率0.9，變異率0.01，找到最優解的概率約為70%，平均時間2.2 s。輸出結果如圖8所示。

4.2 蟻群算法對最優路徑的計算

螞蟻個數選取100，轉移選擇因子選0.2，信息素蒸發系數選0.8。其最優解概率約為80%，平均搜索時間為3.0 s。輸出結果如圖9所示。

4.3 遺傳+蟻群混合算法

參數選擇同上，使用遺傳算法優化初始信息分布和求解過程中的解分布。最優解概率約為96%，平均時間為3.5 s。輸出結果如圖10所示。

4.4 仿真結果分析

由表3中的仿真結果可以得出，遺傳算法在速度上存在優勢（高于蟻群算法25%），蟻群算法則在精確度方面表現良好（高于遺傳算法13%）。當節點數目較少時，混合算法在精確度方面得到了提高（12%），但速度方面略微下降（-14%）。這是由于在進行蟻群算法時，為進一步提高精確率進行遺傳操作增加了一定時間，此時間大于用遺傳算法優化蟻群解分布節約的時間，從而得到的結果是最優解概率得到提升，算法時間增加。但當節點數目增加到100時，混合算法在精確度（10%）和時間（15%）上都有所提升，故在節點數目足夠多時，混合算法相對于單一的算法，集成了二者的特點。

5 試驗測試

考慮到實際項目需求（集成事故預警與事故鏈阻斷系統，本文未涉及），將系統放于車載終端上硬件資源（arm11開發板）可能出現資源不足，故將最優路徑的計算放于后臺服務器。測試連接原理圖如圖11所示。

車載端用于人機交互，主要用于數據的傳輸和地圖的顯示。車載端為基于安卓的嵌入式ARM板。OBU與RSU為DSRC無線通信模塊，OBU用于與RSU的通信，RSU主要用于部分數據的采集工作與通信。后臺為一臺PC機，主要用于最優路徑的計算。

圖12為車載端圖，車載DSRC（OBU）為方便安裝信號天線置于車頂，由于試驗條件所限，實時的平均行程速度和流量數據由兩輛汽車的數據平均而來。

圖13為路側端，試驗時放于路邊。實時數據的獲取方式如圖14所示。

實時數據獲取途徑如下。

平均行程速度：首先，車載端通過由裝于OBD接口的北斗云藍牙OBD-2模塊（圖14（b）中左上角白車與右邊黑車）獲取自車速度，并將自車速度通過圖14（a）中的移動RSU（路側通信單元）和（b）中左上方小紅車上的RSU傳給后臺，后臺將車速平均得到近似平均行程速度。

交通流量：RSU的無線范圍約為500 m，兩臺移動RSU和兩臺固定RSU統計約2 000 m內的車流量，得到近似交通流量。

飽和度：由裝于交叉口的兩臺固定RSU計算飽和度。

行車間距：由4臺RSU根據車輛方位近似計算。

信號交叉口違規概率、貨車超載比等由歷史數據進行近似。

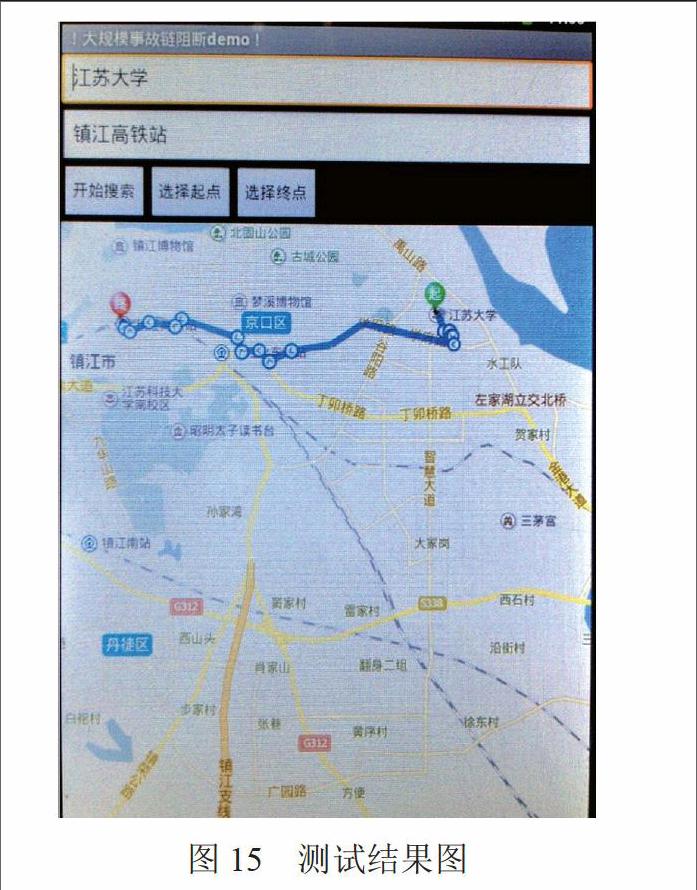
測試結果如圖15和圖16所示。

測試為在車載端輸入起點與終點（移動RSU放于天橋路），然后傳給后臺。

如圖15所示，起點選擇為江蘇大學，終點選擇為鎮江高鐵站，兩點間直線距離為8.2 km，兩點間節點數量為67個。顯示的最優路徑全長10.3 km，計算時間約為5 s，準確率接近100%。對比仿真試驗時間略微增加（約1 s左右），經過對比后發現是ARM板與后臺的通信過程中耗費了一定的時長。

如圖16所示，選定起點與終點后，改變某路段的擁擠度值或安全度值并到達一定閥值，路線會發生相應的改變。為排除規避擁擠、規避已發事故、規避潛在事故間試驗的相互影響，測試時選擇相同道路（天橋路）進行改變。

由表4和圖16可得出，當實時的擁擠狀況和安全狀況發生改變且到達一定的閥值時，最優路徑會發生相應的改變，達到了規避擁擠和規避潛在事故的目的。當標記某段道路為事發路段后，同樣可以達到規避已發事故的目的。

6 結論

（1）利用模糊控制對動態路阻進行了量化，采用遺傳蟻群的混合算法對最優路徑進行求解，并進行了Matlab仿真和實地試驗。

（2）仿真結果表明，當節點數目較小時，混合算法在精確度上具有明顯優勢，但在時間上略微增加。當達到一定的節點數目時，混合算法綜合了遺傳算法與蟻群算法的優勢，在時間和精確度上都有提高。

（3）試驗結果表明，使用該模型和算法可以求解得到實時的最優路徑，且該路徑能達到規避擁擠、規避潛在事故和規避已發事故的目的。

參考文獻（References）：

祝付玲， 王煒. 城市道路交通擁堵評價指標體系研究[D]. 南京：東南大學，2006.

Zhu Fuling，Wang Wei. Research on Index of Urban Traffic Congestion Measures [D]. Nanjing：Southeast University， 2006.（in Chinese）

HUANG C J，WANG Y W，CHEN H M，et al. Application of Cellular Automata and Type-2 Fuzzy Logic to Dynamic Vehicle Path Planning [J]. Applied Soft Computing，2014，19（2）：333-342.

李云，謝剛. 基于遺傳算法的動態路徑優化 [D]. 太原：太原理工大學， 2010.

Li Yun，Xie Gang. Dynamic Path Optimization Based on the Genetic Algorithm [D]. Taiyuan：Taiyuan University of Technology，2010.（in Chinese）

李相勇， 張南， 蔣葛夫. 道路交通事故灰色馬爾可夫預測模型 [J]. 公路交通科技，2003（20）：98-100.

Li Xiangyong，Zhang Nan，Jiang Gefu. Grey-Markov Model for Forecasting Road Accidents [J]. Journal of Highway and Transportation Research and Development， 2003（20）：98-100.（in Chinese）

賈順平，於毅. 城市道路交通狀態判別方法研究 [D]. 北京：北京交通大學， 2007.

Jia Shunping，Yu Yi. Research on the Identification Method of Urban Road Traffic Conditions [D]. Beijing：Beijing Jiaotong University，2007.

韓悅臻，曹三鵬. 城市道路交通狀態指標體系設計探討[J]. 公路，2005（6）：121-123.

Han Yuezhen，Cao Sanpeng. Research on the Index System of Urban Road Traffic State [J]. Highway，2005（6）：121-123.（in Chinese）

徐建閩，孫超.城市道路交通狀態評價分析研究 [D].廣州：華南理工大學，2010.

Xu Jianming，Sun Chao. Research on Urban Traffic Network State Evaluation and Analysis [D]. Guangzhou：South China University of Technology，2010.（in Chinese）

郝媛，徐天東，孫立軍. 基于模糊的城市快速路交通流狀態判別 [J]. 公路工程，2008，33（2）：94-99.

Hao Yuan，Xu Tiandong，Sun Lijun. Fuzzy Logics Based Traffic State Identification on Urban Expressway [J]. Highway Engineering，2008，33（2）：94-99.（in Chinese）

孟祥海， 鄭來， 秦觀明. 基于模糊邏輯的交通事故預測及影響因數分析 [J]. 交通運輸系統工程與信息， 2009， 9（2）：87-92.

Meng Xianghai，Zheng Lai，Qin Guanming. Traffic Accidents Prediction and Prominent Influencing Factors Analysis Based on Fuzzy Logic [J]. Journal of Transportation Systems Engineering and Information Technology，2009，9（2）：87-92.（in Chinese）

Yu Shiwei，Ding Chang，Zhu Kejun.A Hybrid GA-TS Algorithm for Open Vehicle Routing Optimization of Coal Mines Material [J]. Expert Systems with Applications，2011，38（8）：10568–10573.

?ATAY B. A New Saving-Based Ant Algorithm for the Vehicle Routing Problem with Simultaneous Pickup and Delivery [J]. Expert Systems with Applications，2010，37（10）：6809–6817.