廈門海滄體育中心體育場風荷載數值模擬計算
匡子佑,肖偉,楊瑪莎,徐洪勇
(廈門合道工程設計集團有限公司 福建廈門 361002)
1 提出問題
圖1 海滄體育中心整體效果圖
海滄體育中心由主體育場、游泳館、綜合館、門球館等組成(圖1)。主體育場長軸 292m,短軸 200m,鋼結構屋蓋最高點高度為32m,由東西看臺組成,看臺最大懸挑32m(圖 2,圖 3),體型呈現開敞橢球形。該屋蓋結構質量輕、柔性大,風荷載為控制屋面結構設計的主要荷載;同時,該結構位于大氣邊界層中處于風速變化大、湍流度高的區域,再加上屋面形狀多不規則,《建筑結構荷載規范》中未規定對應可查詢的風荷載體型系數,規范建議該類風荷載敏感的結構宜通過風洞試驗確定體形系數。本文體育場為例,在風洞尚未進行的情況下,利用風數值模擬求得風荷載體型系數進行初步設計;在風洞試驗進行之后,與風洞試驗結果進行對比,分析數值模擬結果的精度和可靠性,探討數值風洞的模擬方法和該結果用于初步設計的合理性。
2 數值模擬計算
2.1 風荷載數值模擬分析過程

圖2 體育場建筑效果圖圖3體育場結構計算模型
a.根據研究對象的幾何尺寸建立物理模型,確定計算流域的范圍,保證流域足夠大能消除邊界對研究對象的影響。
b.根據實際情況選擇合理的網格形式。
c.選擇基本方程并根據研究的問題和需要的精度,確定所需要的湍流模型。
d.空氣的相關參數的設定。
e.根據實際來流條件確定相應的邊界條件。
f.根據求解精度的需要和促進迭代計算收斂的需要,調節各項的控制參數,收斂標準等。
g.計算和求解,進行迭代計算直至滿足收斂標準。
h.檢查結果,保存結果,如果結果不理想,還需要繼續調整網格,改變數值和物理模型。
2.2 數值模型選擇
本文數值模擬選用k-ε模型,壓力與速度耦合方式為simple算法,收斂精度取值0.00013,經過計算,能夠較好的收斂。
2.3 模型建立
主體育場模型以全尺寸模型建立,模型中心位于地面長軸方向距離風洞入口1/3處,計算域尺寸為長×寬×高為1500×1000×350m,網格采用非結構化網格,網格數量約為400萬(圖4、圖5)。
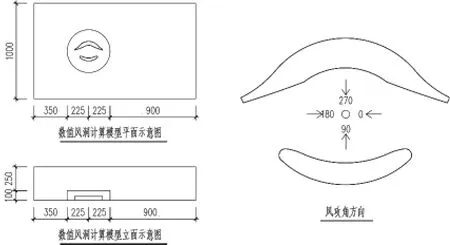
圖4 計算模型示意圖
2.4 邊界條件設置
入口風剖面:
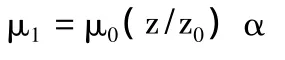
其中,μ1為垂直高度z位置的水平風速,μ0為參考高度 z0位置的風速;本工程數值模擬取值 μ0為 15m/s;本工程地面粗糙度為A類,故α取值為0.12。
湍流強度:


圖5 計算模型局部圖
zG取值為350m
壁面條件:
數值風洞表面和側面采用自由滑移,壁面上速度為0。
出口條件:
出口位置認為湍流已經充分發展,沿流動方向沒有變化,即為勻速,故各變量法向導數為0。
3 結果分析
3.1 數字模擬結果特性分析
各風向角下屋蓋及其周圍的整體的風壓分布云圖如(圖6、圖7)所示,可以看出,體育場屋蓋主要受負壓作用,尤其在邊緣處局部負壓較大。對于該大懸挑屋面分析其在各個風向下的風壓分布,限于篇幅,本文取典型的0°和270°來 進行分析。
0°風向角時,即是風從東側吹到西側,順著屋蓋長的方向。該方向上南北懸挑屋蓋表面風壓分布規律大致相同,上表面為負壓,下表面也為負壓,上表面負壓絕對值略大于下表面負壓,上下疊加結果整體表現為負壓;南北懸挑屋蓋最大風壓均出現在外邊緣處,且邊緣離風入口最近處風壓最大;由于南北懸挑屋蓋內側邊緣處趨于平緩,體育場屋蓋為開敞結構,該位置風壓接近為0。

圖6 0°風向平均壓力系數分布圖
270°風向角時,即是風從北側吹到南側,垂直于屋蓋長方向。該方向上南北懸挑屋蓋表面風壓分布沿著南北中心線呈現左右對稱的規律,北懸挑屋蓋上下表面風壓均為負壓,上表面負壓絕對值較大,外邊緣離風入口最近處風壓最大,體形系數達到約-3.7,從外邊緣到內邊緣,風壓梯度減小;南懸挑屋蓋由產生兜風效應,故而上表面風壓為負壓,下表面風壓為正壓,上表面負壓和下表面正壓絕對值均也較小,整體表現為向上的吸力。
3.2 風洞試驗結果簡介

圖7 270°風向平均壓力系數分布圖(數值模擬)
本工程委托中國建筑科學院風洞實驗室進行試驗,試驗模型縮尺比例為1:200(圖 8),試驗采用美國Scanlivalve公司最新的電子壓力閥掃描系統DSm3400對模型表面進行平均和脈動壓力測量,試驗風速為15m/s,采樣時間為21s。從風洞試驗室提供的文本來看,數值模擬與之規律是一致的。

圖8 風洞試驗模型
4 數字模擬與風洞試驗結果對比
4.1 結果對比
本文通過對風洞試驗和數值模擬結果進行整理(圖9~13),分別對比屋蓋中間大面積區域和邊緣突變處兩者風壓體型系數數值的差異,結果見(表1)。
從(表1)對比可以看出,整體數值上來看,風洞試驗結果大于數值模擬結果。具體到各個位置,除部分風壓絕對值小于0.5區域以外,屋蓋大部分區域兩者偏差均在25%以內,誤差最大為270度風攻角時的北懸挑屋蓋外邊緣處。
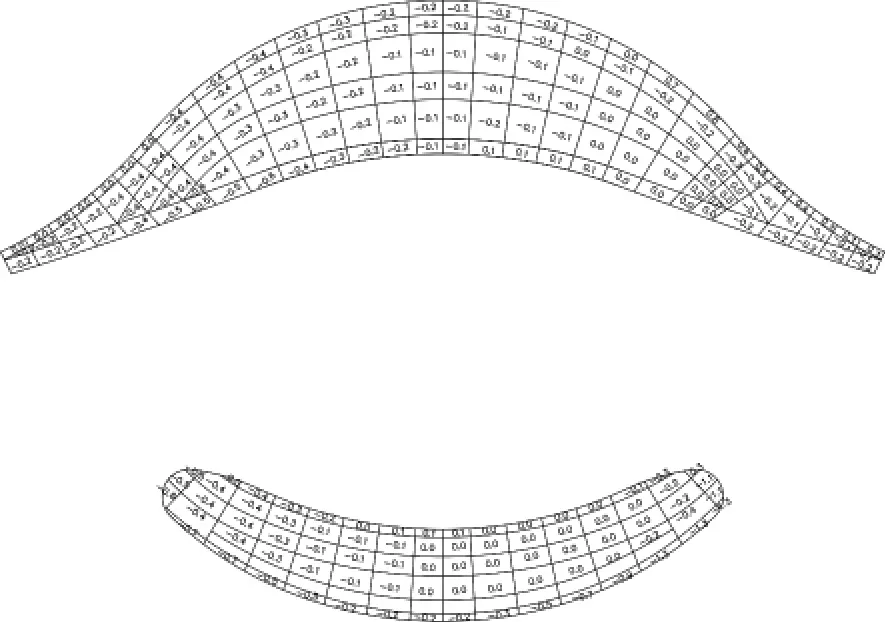
圖9 0°風向平均壓力系數分布圖(風洞試驗)
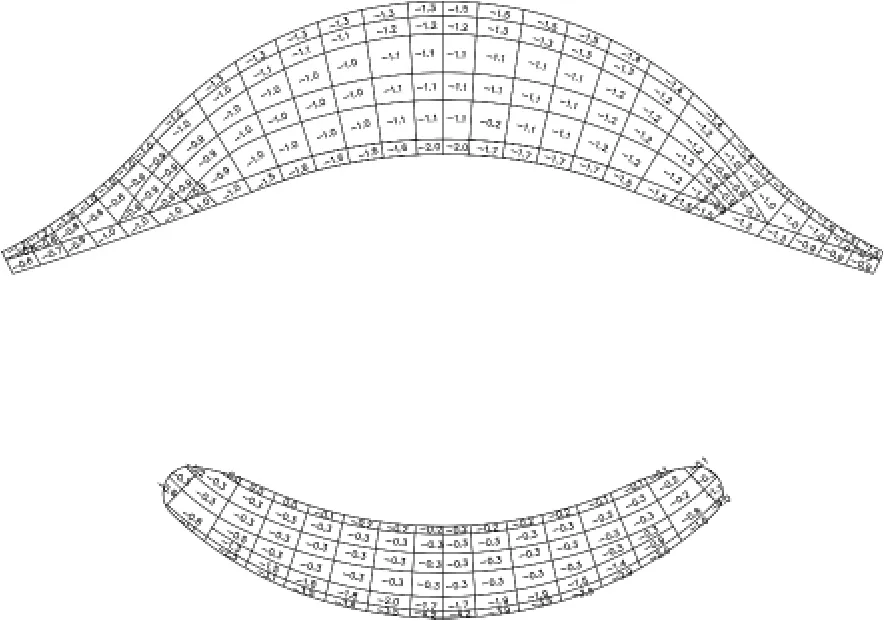
圖10 90°風向平均壓力系數分布圖(風洞試驗)
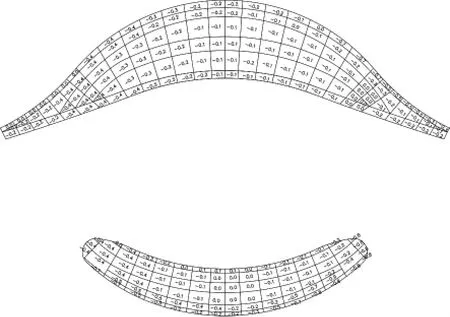
圖11 0°風向平均壓力系數分布圖(數值模擬)
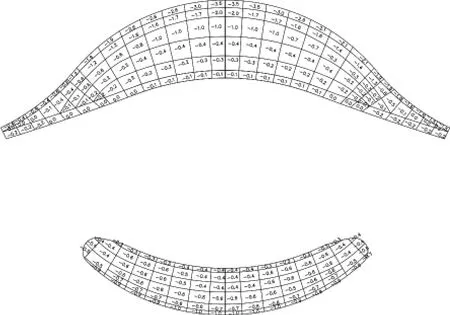
圖12 90°風向平均壓力系數分布圖(風洞試驗)
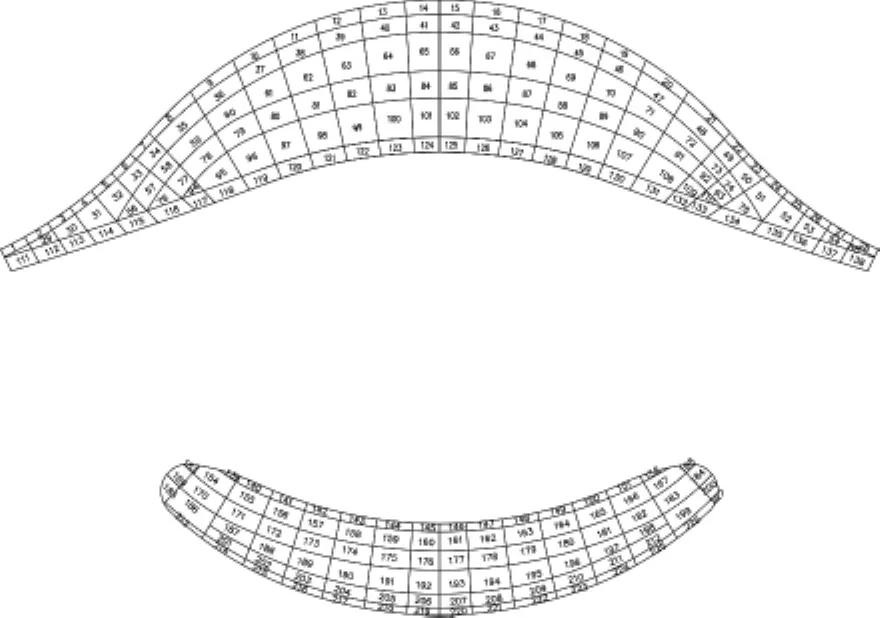
圖13 數據整理網格圖
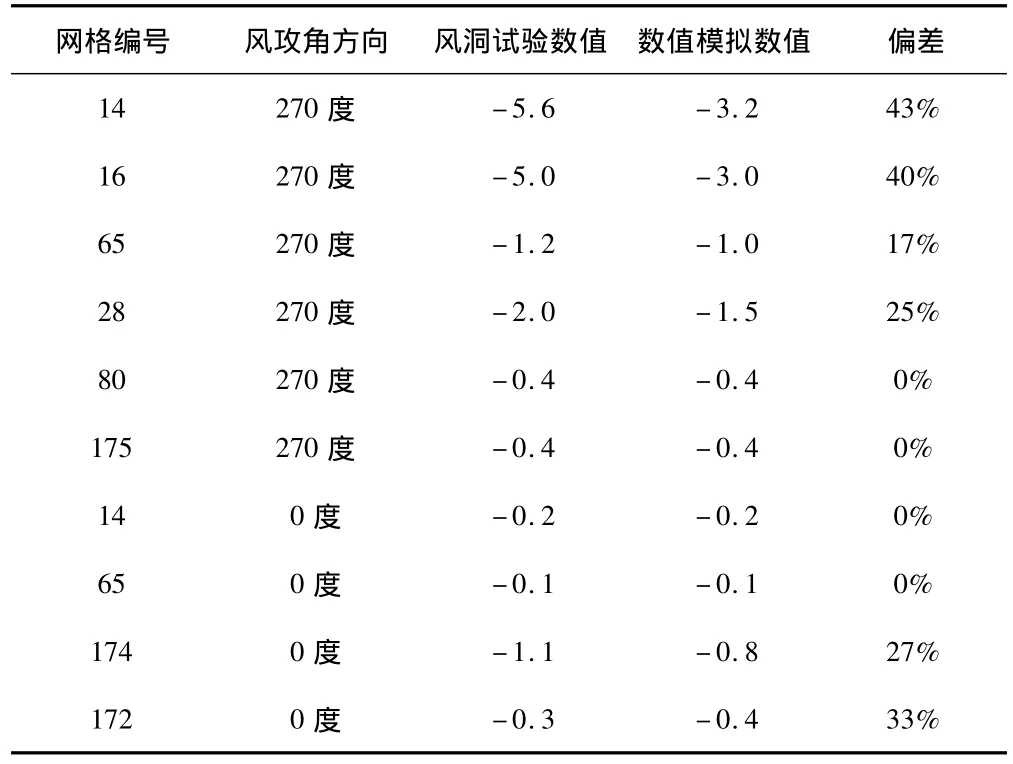
表1 結果對比
4.2 誤差分析
a.模型誤差:體育場館幾何模型建模和網格劃分難度較大,計算機的計算能力有限,模型不能建立得十分精確,計算時網格數量不能劃分得足夠精細,并且收斂誤差取值0.00013略微偏大;
b.模型誤差:邊界條件不能完全吻合,入口的風剖面、粗糙度等不能完全模擬風洞試驗的環境,導致流體在建筑物周圍產生漩渦、分離等與試驗有一定的差別,局部誤差較大;
c.方法誤差:數值模擬方法采用的是足尺度建模,而風洞實驗采用的是幾何相似、動力相似和來流條件相似的縮尺寸模型。
5 總結
(1)對海滄體育中心體育場風荷載進行數值模擬,并將體育場屋蓋風荷載的數值模擬結果與已有的風洞試驗數據進行比較,風荷載體型系數基本規律相同,屋蓋中間大面積區域數值結果相近,雖然邊緣處誤差較大,但該位置面積較小,初步設計時雖然局部荷載計算不足,對整體結構指標影響不大,施工圖階段只需調整少數構件即可,從而說明數值模擬在初步設計階段,作為結構設計的依據是可靠的。
(2)相比風洞試驗,數值模擬具有以下幾個特點和優勢a.費用低,所需周期短、效率高;b.可以進行全尺度的模擬,能克服邊界層風洞試驗中難以滿足雷諾數相似的困難;c.數值模擬方法有可視化的數據結果,可以提供風洞試驗不便或無法提供的繞流流場信息。
(3)在風洞試驗階段,數值模擬結果對于風壓測點布置具有一定的指導意義。
(4)通過對體育場風洞試驗和數值模擬結果對比研究,發現對復雜大跨結構數值模擬精度有待進一步提高,特別是高負壓處和邊緣區域的局部誤差較大。
[1]黃本才,汪叢軍.結構抗風分析原理及應用[M].同濟大學出版社.2008(2).9.
[2]孫曉穎,朱曉潔,武岳,等.深圳大運會主體育場罩棚風壓分布的數值模擬[J].哈爾濱工業大學學報.2010.8.
[3]海滄體育中心風洞測壓試驗報告[D].中國建筑科學院.2012.2.

