3D Hough Transform在激光點云特征提取中的應用

李明磊，李廣云，王 力，李海波，范哲瑞

(1.信息工程大學導航與空天目標工程學院，河南鄭州450052;2.68029部隊，甘肅蘭州730000;3.66240部隊，北京 100042)

一、引 言

近年來，激光掃描測量技術得到了飛速發展，測量速度從每秒幾千個點提升到百萬量級，測量精度在一定距離內可達到毫米級甚至亞毫米級;其應用范圍幾乎涵蓋所有傳統測繪的應用領域，包括地形測繪［1］、礦山測量［2］、變形監測［3］、文物保護［4］、虛擬現實［5］、數字城市［6］、逆向工程［7］等。激光掃描測量技術大幅減少了外業數據采集的時間和工作量，內業數據處理成為項目的工作重心，也是難點所在。對激光點云數據進行處理、挖掘點云數據信息是當前激光掃描測量技術的研究熱點之一。特征提取方法作為二維圖像處理的重點研究對象，在三維激光點云數據處理中也存在類似的研究價值，其不僅可以用來進行多站點云的快速自動拼接，還可以用于點云的簡化及后續的建模等任務。Paul Hough［8］于 1962 年提出 Hough transform(HT)，用于二維圖像中的直線檢測，目前已發展出多種形式，包括直接由二維HT導出的standard Hough transform(SHT)，以及改進的 fast Hough transform(FHT)［9］、probabilistic Hough transform(PHT)［10］和randomized Hough transform(RHT)［11］等。二維 HT 可以容易地擴展到三維空間，即三維Hough transform(3D-HT)。本文在分析三維激光點云特點的基礎上，以點云中平面特征的提取為例，研究將3D-HT用于點云特征提取所涉及的關鍵技術。

二、Hough transform原理

1.二維HT直線探測原理

在二維圖像空間，每一個像素點在笛卡爾坐標系中都有一個明確的二維坐標(x，y)，如果圖像中某一特征能用函數F進行數學表示，則此特征上的所有像素點都應滿足由函數F變換得到的等式。以二維直線特征為例，函數F用式(1)表示。式中，θ取任意角度圖像中每一個像素點(x，y)都能在二維Hough空間找到對應的Hough變換后的坐標(θ，ρ)。其中θ和ρ的幾何意義是:從原點O向過點P的直線F作垂線L，L與x軸之間的夾角即為θ，ρ為原點O到直線F的垂距，如圖1所示，圖中FON(foot of normal)表示L與F的交點。

之后利用二維累加器(θ方向按角度劃分為若干段，ρ方向按距離數值劃分為若干段)將二維Hough空間的點坐標θ和ρ分別按照角度和距離進行累加統計，即對于累加器中的任一角度θ1，利用式(1)求出對應的 ρ1，累加器中(θ1，ρ1)處進行一次累加，這個過程也被稱作投票。如果二維圖像中存在一條直線，其參數為(θ0，ρ0)，則累加器累加結果在(θ0，ρ0)處存在一個峰值。每個峰值代表一條直線，因此下一步任務就是對累加器的累加結果進行局部峰值的探測。峰值探測最常用的方式是通過劃定一個閾值來確定各個峰值的分布，提取出各個票數高于閾值的峰值。

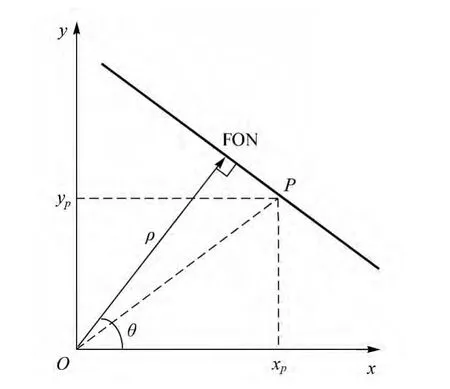
圖1 二維空間直線的Hough變換

2.三維SHT平面識別原理

對于三維激光點云的特征識別，對二維HT增加一個參數φ就可以比較容易地擴展到三維HT。如果三維空間中某一特征可以用函數F進行數學表示，如平面、球、圓柱等，3D-HT就可以以某種適當的方式對此特征進行識別。以平面特征為例，在三維笛卡爾坐標系中，F一般表示為

為確定某一平面，必須利用這4個參數a、b、c、d，由于4個參數的取值范圍是不確定的，直接以這4個參數進行投票時累加器無法確定范圍和投票間隔。因此，3D-HT采用式(3)表示平面特征，將平面參數轉換為角度信息。

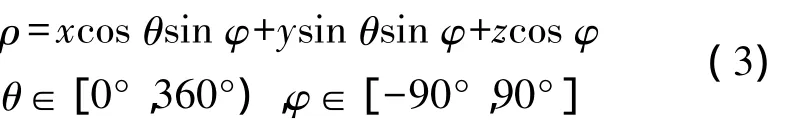
式中，參數θ表示平面的法向n在xoy平面中的投影和x軸正向之間的夾角;φ表示n和xoy平面的夾角;ρ表示原點O距離平面的距離，如圖2所示。

以nφ表示在φ方向將三維Hough空間劃分的段數，以nθ表示在θ方向劃分的段數，以nρ表示在ρ方向劃分的段數，則三維Hough空間共被三維劃分為nθ×nφ×nρ塊，用作累加器的分區，以進行下一步投票。事實上三維空間中過點P的平面有無窮多個，而由于對三維Hough空間的離散化劃分，平面個數被限制到 nθ×nφ個(θ和φ 確定后代入式(3)，ρ也可確定，故個數為 nθ×nφ)，這也就意味著對于每一個點P，需要找到這nθ×nφ個滿足式(3)的平面(按劃分間隔逐個尋找)，即每個點P在三維累加器中需要投票nθ×nφ次。假設點云中共有N個點，則累加器整個過程就需要N×nθ×nφ次。最終在累加器累加結果中，局部峰值點表示可能存在的平面。

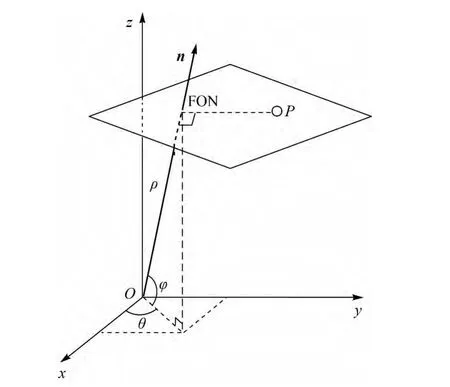
圖2 三維空間平面的Hough變換

上述過程即為利用三維標準Hough變換(3DSHT)對平面特征進行識別。從其過程的實現來看，此方法耗費的時間和計算資源較大，因此許多改進算法被用于改善標準Hough變換效率低、耗空間等問題。

三、3D-HT平面提取新方法

僅用三維點的笛卡爾坐標進行3D-SHT平面特征識別還可能會存在一些問題。如圖3所示，內層平面和外層平面(就平面本身來說是三維無限的)雖然相交，但事實上卻沒有相交的點，但3D-SHT識別的結果是將外層平面上與內層平面理論相交的點也識別為內層平面上的點。為解決這個問題就需要對3D-SHT額外增加相應的限制條件，這樣的限制條件并不容易找到，而且適用性不一定廣泛。從3D-SHT原理來看，此方法僅利用各個點的三維坐標信息，并且將各個點單獨考慮，沒有利用各點之間的相互關系，而且每個點對360°范圍內任意傾角φ和θ的平面都要投票(求出任意傾角φ和θ相應的距離常數ρ)，存在變換效率低、耗空間等缺點。事實上對激光點云進行處理時至關重要的一步就是確定各點之間的關系，以此為基礎才能對點云進行下一步分析處理，本文嘗試以此種思路出發提出3D-HT的新方法。

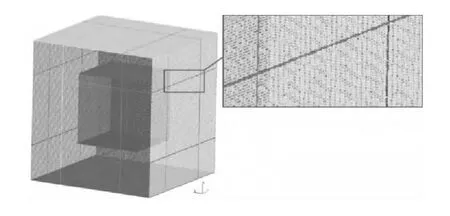
圖3 3D-SHT平面識別結果

首先利用數據結構快速恢復點云之間的鄰近關系，進而估計每個點的法矢(法向計算與重定向)。激光點云中每個點的法向是指該點及其臨近的若干點確定的三維表面在此點處的法向。激光點云的法向信息是激光點云數據處理中的一個極其重要的信息，對激光點云進行法向計算也是其數據處理中很重要的一步，之后利用恢復出的每個點的法向信息進行HT的投票。每個點只投票一次，降低投票的次數;利用法向信息進行投票，利用到了點與點之間的鄰接關系，每個點與其鄰近點的法向比較近似，一般不會發生突變，圖3所示的錯誤識別問題也可解決。

具體過程如下:

1)利用數據結構對點云進行分塊，從而可以迅速確定點之間的鄰接關系，加快對每個點鄰近點的搜索速度，本文中數據結構采用的是八叉樹［12］。利用八叉樹對某模型的點云數據進行分塊的效果如圖4所示(視圖的方向逆著y軸方向，故只能看到二維效果)。

圖4 八叉樹分割效果

2)利用數據結構尋找點P0的k個鄰近點，用這些點進行最小二乘平面擬合(按式(2)進行)［13］，并依次以此方式計算各個點的法向。算得的法向方向具有二向性(可能與實際情況相反)，通過從某點出發進行鄰近傳遞可對其進行調整。而對于激光點云，每個點的法向n=(nx，ny，nz)T必定逆向激光的入射方向r=(x，y，z)T，因此只需保證式(4)中 d為負，即可調整法向到正確指向。

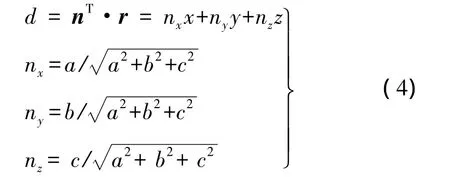
3)將各個點的法向轉換為式(5)所示的以角度和距離參數表示的形式，以利于投票過程的執行。

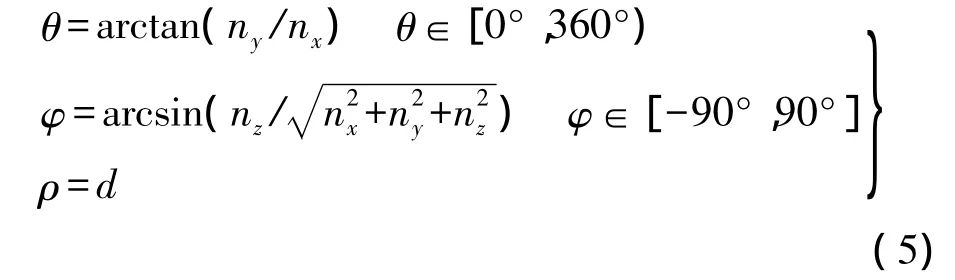
4)確定累加器的劃分間隔，利用各點變換得到的(θ，φ，ρ)進行投票。

5)局部峰值探測，從而找出點云中可能存在的各個平面。

6)利用歸類到各個平面上的點集重新按照式(2)進行抗差最小二乘平面擬合［13］，以使提取的平面具有更好的平面度。

從執行過程可以看出，該方法比較充分地利用了激光點云預處理得到的成果(鄰近關系的確立、法向的計算與重定向等)，在步驟4)的投票過程中假設點云共有N個點，此方法也就僅需要投票N次，遠遠少于3D-SHT的N×nθ×nφ次，大大降低了投票過程的復雜度。

由于法向計算方式的影響，在墻角等特征突變點附近的法向計算結果一般是不正確的，因此墻角等處的點集也就不能通過HT進行有效識別。本文方法在步驟6)重新進行了抗差最小二乘平面擬合，得到的不僅有平面法向參數(a、b、c)，還有平面到原點的距離參數d，即激光三維點云笛卡爾坐標系下完整的平面方程式，在平面上的點一定滿足相應的平面方程。據此可對法向計算結果錯誤的特征突變點及其附近點等進一步歸類，分離出墻角點等特征突變點:

1)由于墻角點滿足步驟6)結果中兩個以上的平面方程(平面的交點)，依此可以有效地將其分離出。

2)將墻角點附近點的坐標分別代入步驟6)平面方程式，可以將其重新歸類到其應在的平面，并且其法向計算結果也可以得到修正。

四、試驗驗證

首先是累加器劃分間隔的具體確定方法。本文利用Rigel公司的VZ-400掃描儀對某實驗室的普通墻面(一般建筑內部的常用墻面具有較好的代表性)進行精掃，如圖5所示。圖5(a)是對墻面拍攝的照片;圖5(b)中上圖為在掃描結果中選取墻面比較平整的點云塊，下圖為點云法向計算結果添加光照顯示的效果;圖5(c)為將對每個點算得的單位化后的法向(包含3個方向的分量)作為三維坐標顯示(分布在半徑為1的球面上)的效果，由于墻面不平整、激光掃描儀誤差、法向計算誤差等因素的影響，對墻面點云算得的法向并不完全相同(若完全相同，圖5(c)所有點都重合為一個點)。

圖5 實驗室墻面照片與點云

對墻面的法向計算結果進行統計，結果見表1。由于y軸與墻面的夾角最大，接近垂直，故其方向誤差較小。由于 sin(1°)=0.017 5，對于兩個單位向量，坐標差別0.017 5相當于夾角差別接近1°。根據法向計算的中誤差將累加器中角度的劃分間隔設置為1°(法向夾角小于1°的兩個點當作處于兩個平行平面上的點，根據距離參數確定兩平面是否重合)，根據實際平面特征分布，將距離劃分間隔設為5 cm(距離小于5 cm的兩平行平面當作同一平面，間隔太小無意義且增加空間消耗，太大則不能有效識別平面特征)。

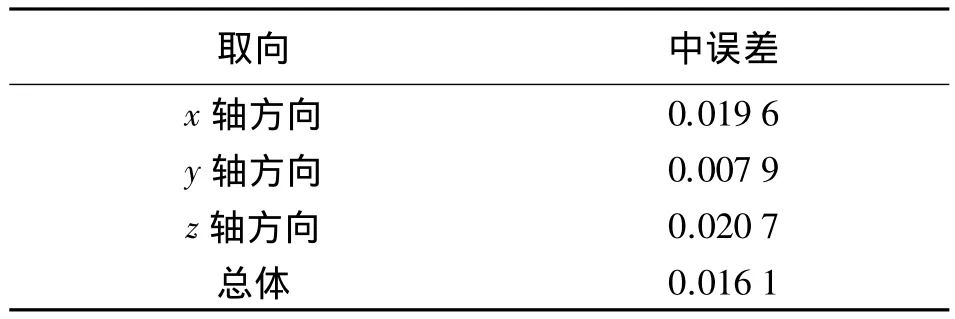
表1 墻面法向中誤差

為測試本文方法的有效性，首先利用兩層立方體模擬數據(共12個平面，303 612個點)進行試驗。圖6即為平面識別的效果，不同的平面之間用不同的顏色來區分。圖6(a)所示，由于一般的鄰近點平面擬合不能有效計算得到正確的法向，故在平面相交處的點(邊角點)并未被有效識別。而通過本文特征突變點及其附近點重新歸類的思路(修正方案)，可以有效地對其重新歸類，將平面和墻角分離，效果如圖6(b)所示。表2為對模擬數據進行平面提取的輸出結果(轉換成式(2)的4個參數，并記錄平面上識別到的點數)，與圖6數據模擬時的設定值基本符合(內層平面完全符合，外層平面由于內層平面與其交線的影響有個別點仍未有效歸類)。

圖6 兩層立方體數據平面提取效果

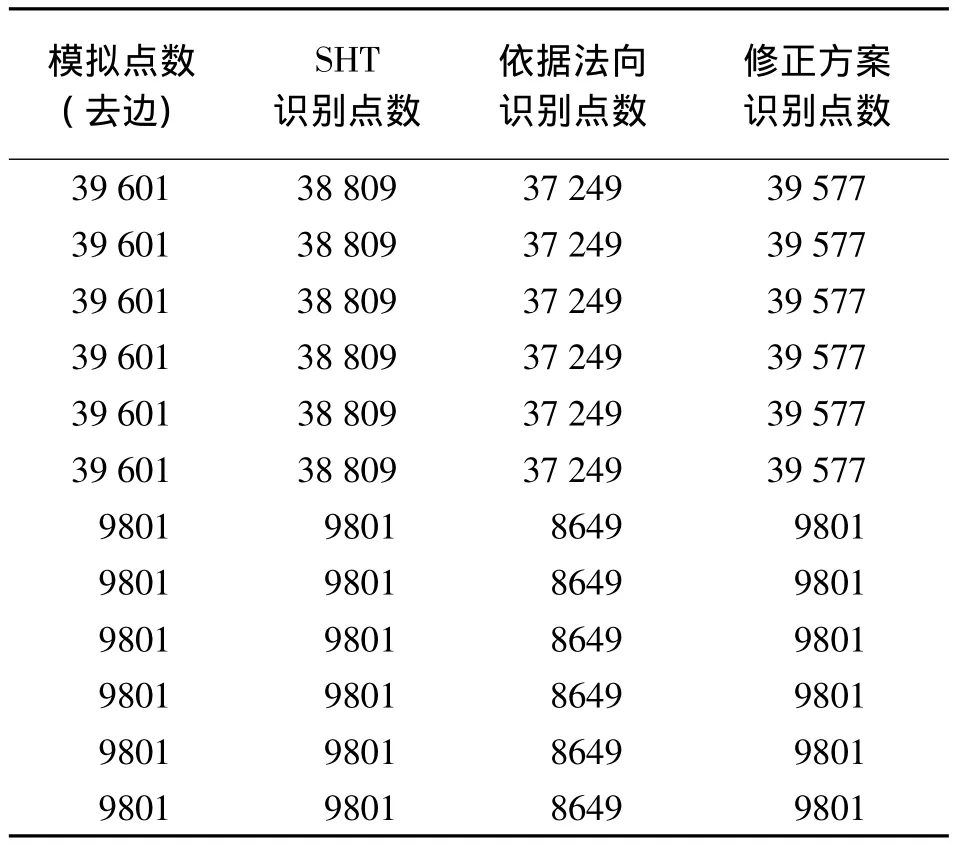
表2 兩層立方體數據平面提取結果

為測試本文方法的實用性，利用某實驗室內部激光掃描實測數據進行試驗。圖7即為平面識別的效果，圖7(a)為僅依據法向投票識別的效果，圖7(b)為利用修正方案識別的效果，圖7(c)為將分離出的墻角顯示的效果。最終平面提取結果為6個，與實際符合，而且墻面墻角特征可以有效分離。

圖7 激光實測數據平面提取效果

五、結束語

本文根據激光點云數據處理的特點，結合激光點云數據預處理中點與點之間鄰近關系的確立及法向的計算與重定向，提出了直接根據每個點法向進行Hough變換的方法，極大地降低了3D HT的復雜度，并可以有效解決3D-HT存在的錯誤識別問題。對特征突變點及其附近點的重新歸類方法可以進一步識別大部分沒有正確識別的特征突變點，并可以對其法向計算結果進行修正。本文提出的方法僅受法向計算結果制約，具有良好的適用性。試驗中首先利用普通常見墻面的激光掃描儀精掃數據確定了三維累加器的劃分間隔，之后分別利用模擬數據和實測數據證明了該方法的有效性和實用性。

本文的工作主要集中于激光三維點云平面特征及相應墻角輪廓的提取，下一步可以以此為基礎研究更多種類特征的提取方法。

［1］許映林.3維激光掃描技術在溫泉水電站大比例尺地形圖測量中的應用［J］.測繪通報，2007(6):9-13.

［2］楊青，張亮，王振.基于KD樹和CDT的露天礦三維建模［J］.計算機技術與發展，2011，21(12):224-226.

［3］譚國銓.3D激光掃描儀在電廠冷卻塔變形監測中的應用探討［J］.勘測設計，2009(4):30-32.

［4］周俊召，鄭書民，胡松，等.地面三維激光掃描在石窟石刻文物保護測繪中的應用［J］.測繪通報，2008(11):68-69.

［5］李暉，吳祿慎.三維激光掃描技術在虛擬現實中的應用［J］.南昌大學學報:工科版，2007，29(3):239-242.

［6］趙海瑩，張正鵬.三維激光點云數據在城市建模中的應用［J］.城市勘測，2009(1):69-72.

［7］馬有良，李占峰.三維激光掃描儀在曲面逆向工程中的應用研究［J］.機械設計與制造，2009(10):85-87.

［8］HOUGH PV C.Method and Means for Recognizing Complex Patterns:US，Patent 3069654［P］.1962-12-18.

［9］OGUNDANA OO，COGGRAVE CR，BURGUETE R L，et al.Automated Detection of Planes in 3-D Point Clouds Using Fast Hough Transforms［J］.Optical Engineering，2011，50(5):053609.

［10］KIRYATI N，ELDAR Y，BRUCKSTEIN A M.A Probabilistic Hough Transform ［J］.Pattern Recognition，1991，24(4):303-316.

［11］XU L，OJA E，KULTANEN P.A New Curve Detection Method:Randomized Hough Transform(RHT)［J］.Pattern Recognition Letters，1990(11):331-338.

［12］邢坤.海量激光掃描測量數據的處理［D］.鄭州:信息工程大學，2009.

［13］李明磊.點云平面擬合新方法［J］.測繪通報，2012(S1):84-87.