陸面過程模型中垂直非均勻土壤的水分傳輸及相變的模擬

李倩 孫菽芬

1 中國科學院大氣物理研究所季風系統研究中心, 北京100190

2 中國科學院大氣物理研究所大氣科學和地球流體力學數值模擬國家重點實驗室, 北京100029

1 引言

土壤濕度是控制陸面與大氣相互作用的一個重要變量（Shukla and Mintz，1982；Koster et al.,2004）。它可以通過對地表蒸發及其他地表能量通量的影響來影響天氣過程。土壤濕度的異常可以持續幾個月，雖然缺乏足夠的觀測事實證明土壤濕度對于降水的影響，但是它對降水的作用在大氣環流模 型 （ Atmospheric General Circulation Model–AGCM）中是常常可見的（Rind，1982；Yeh et al.,1984）。事實上，很多AGCM的研究已經表明，海洋對于夏季中緯度陸地上降水的影響要小于土壤濕度對降水的影響。且考慮了土壤濕度的異常對于降水的季節預報有很好的改進作用（郭維棟等，2007）。

不同復雜程度的陸面模式對土壤濕度的準確模擬關系到陸—氣間水平衡和水交換的模擬結果，因此顯得十分重要（Mahmood and Hubbard，2003）。在現有眾多的陸面過程模型中，對于土壤濕度的定量描述是通過以下兩個方面來實現的：（1）在垂向分布均勻的介質基礎上，基于推廣的達西定律（即Richard方程）來描述土壤水的流動；（2）同時賦以地表土壤不同的水文特征和熱力學特性。但在現實中，土壤質地的垂直非均勻分布是很常見的。很多理論研究（Yeh et al., 1985a，1985b；Mantoglou，1992）和實驗室（Yeh and Harvey，1990；Sassner et al., 1994；Destouni et al., 1994）及野外觀測（Jensen and Mantoglou，1992）已表明，這樣的非均勻性對于非飽和土壤內部的水分輸送有很大影響。且在模型中也顯現出由于土壤特性的垂直非均勻性而造成土壤導水率、水勢等土壤水力性質的非均勻性，進而影響土壤水分平衡和土壤濕度的模擬結果（Mahmood and Hubbard, 2003；Jhorar et al., 2004）。此外，當土壤發生凍融時，土壤中除了有液態水之外還有固態水—冰，即使含水量一樣，冰含量垂直分布的不同也會使土壤的導水率垂直分布不均勻，從而形成水勢大小和梯度的垂直不均勻分布。因此，即使是垂直均質和含水量均勻分布的土壤中，當土壤伴有凍融過程發生時，其水分也會受到由冰含量垂直分布不同而形成的水勢梯度力的驅動而發生流動，這相當于強化了土壤非均勻性的特點。

盡管目前部分陸面過程模型在水分的模擬上通過分層和土壤性質的參數化方案來刻畫土壤的非均勻性，但是不同的模型對于同一土壤模擬的結果還是有差別的。這不僅與模型選用的土壤水性質的參數化方案有關，還與模型如何處理描述土壤水分變化的方案有關。

在土壤水力性質的參數化方面，土壤水分特征關系式是一個重要的水力學關系，如何確定關系式中的各參數，會對模型的模擬結果產生影響。土壤水分特征關系式包括了土壤基質勢與土壤水分的關系以及土壤導水率與土壤水分的關系。且當土壤凍結時，這些關系式中會增加相應的參數（Ck和E）分別將土壤含冰量對土壤水勢和導水率的關系聯系起來，因此相對于未凍結土壤其水分特征關系式會有所變化。Zhang et al.（2007）利用模型對Ck和E的存在對于模擬結果進行了敏感性試驗，其結果表明，當Ck為零，即不考慮含冰量對土壤水勢的影響時，模型就會高估土壤中冰含量而低估液態水含量，土壤溫度的日變化也被低估，潛熱通量偏小。同時，如果E為零，即不考慮含冰量對土壤導水率的影響，有時會出現土壤水分流動過大，造成與實際相悖的某層土壤水過飽和的情況。除此之外，其中與土壤本身性質有關的個別參數是以指數形式對土壤基質勢及導水率產生影響的。而在目前大多數陸面過程模型中這些與土壤質地有關的參數都是根據經驗或者部分實驗室結果而得，具體大小對土壤水分的模擬會產生怎樣的影響需要進一步探討，且對發生凍融的土壤會產生怎樣的影響也尚未有具體分析。

在處理描述土壤水分變化方案方面，目前常用的處理土壤濕度變化的推廣達西定律，即Richard方程是一個高度非線性方程，一般很難有解析解，只有依靠數值解。而在這一求解過程中（包括基本方程的建立和推演，數值求解方法的發展），如果處理不慎、簡化不當就會丟失土壤非均勻性的特征對水流的影響。例如，在Richard方程中，土壤的水分流動速率是由與土壤基質勢梯度有關的項來驅動的。但在一些模型中為了求解方便，將土壤基質勢的梯度項簡單地轉換成與土壤含水量梯度有關的項（張述文等，2009），正是這一轉換就將土壤性質的空間非均勻性和土壤含冰量對土壤水勢的影響丟失了。張述文等（2009）的研究曾明確指出，由于土壤質地在垂直方向上的不均勻性，很多陸面過程模型如果使用土壤濕度的梯度進行描述土壤水分變化，模擬出來的土壤水分是連續分布的，但是模擬的土壤基質勢出現不連續的情況，這是與實際相悖的情形。而用土壤基質勢的梯度進行描述時，模擬出的基質勢是連續的，但是土壤水分是空間分布不均的，這與實際相符，因此在描述非均勻土壤中水流運動時不應該利用土壤含水量梯度來表征水流運動。

基于以上提到的不同模型對土壤水力學特性和土壤濕度變化方程處理的不同，也鑒于未有深入的研究指出不同的陸面過程模型對于表征土壤質地的參數選取方面的敏感性，本文中選用了Li and Sun（2008）發展的簡化的通用土壤模型對土壤水分模擬的敏感性進行試驗研究。研究中選取目前常用的表征土壤水分特征的關系式（Clapp-Hornberger關系式）及不同土壤水分特性參數，并重點考慮了土壤凍結期間土壤濕度的模擬對各參數的敏感性。

2 非飽和土壤中的土壤濕度方程

2.1 陸面過程模型中常用的非飽和土壤濕度方程

基于土壤水分守恒建立的用于描述土壤非飽和流垂直運動的方程可寫為

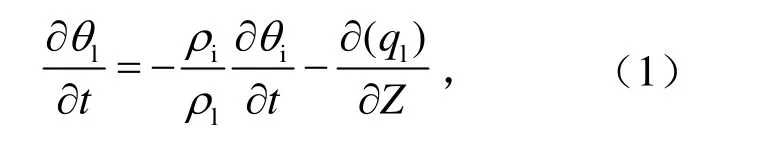
如果土壤未凍結，方程寫為

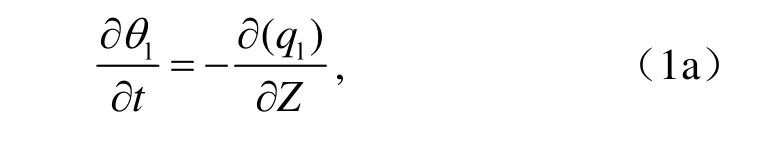
式中，lθ為土壤單位體積液態水含量（m3m-3，文中以下簡稱土壤體積含水量或含水量）；iθ為體積含冰量 (m3m-3)；iρ和lρ分別為冰和液態水的密度(kg m-3)；t為時間 (s)；z為土壤深度 (m)，也代表了豎向的坐標（向下為正）。ql是液態水流通量（向下為正），遵循非飽和介質中推廣的達西定律（即Richard方程），可寫為

其中，ψ為土壤基質勢 (m)，Kl是土壤的導水率(m s-1)；將上式帶入（1）式，得到土壤體積含水量的變化方程：

2.2 土壤水分特征關系式

非飽和土壤中，忽略滲透勢的影響，土壤水分特征曲線表征了土壤水勢和土壤含水量及導水率之間的本構關系。這一本構關系與土壤中土壤顆粒的尺度和分布及孔隙空間的結構有關，隨著土壤質地的變化而變化。根據大量的田間和實驗室采樣試驗可以得出不同土壤質地的水分特征曲線關系式。目前常用的表征土壤水分特征曲線的經驗關系式基本有三種，即Brooks-Corey 關系式（Brooks and Corey，1966）、van Genuchten關系式（van Genuchten,1980）和Clapp-Hornberger 關系式（Clapp and Hornberger，1978）。這三個關系式都是簡潔、方便使用的數學關系式，能與很多的土壤特征曲線擬合得較好。

Brooks-Corey 關系式：

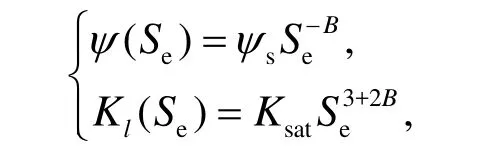
van Genuchten關系式：

Clapp-Hornberger 關系式，也是Brooks-Corey 關系式的簡化和近似：這些關系式中，Ksat為土壤的飽和導水率 (m s-1)；ψs,θs分別為土壤飽和水勢（m；為一負值）和土壤孔隙度（m3m-3）；Se為土壤有效孔隙度；參數B,α,m均為隨著土壤質地而變化的常數 (Burdine，1953)。參數B稱為土壤孔隙大小分布指數，孔隙的大小和分布決定了土壤吸附力和水分之間的關系。根據Clapp and Hornberger 的大量試驗（1978）證明，砂土的參數B最小，粘土的最大。Clapp-Hornberger關系式和Brooks-Corey關系式僅當ψ＜ψs時成立，且當ψ＞ψs時θl=θs。van Genuchten關系式能更好地描述土壤濕度和土壤含水量之間的關系，尤其在土壤接近飽和時，但是由于其復雜的非線性關系，大多數的陸面過程模型并不采用。而用較為簡潔的Clapp-Hornberger 關系式。

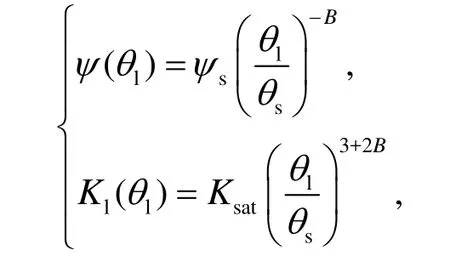
當土壤發生凍結時，冰的存在對土壤水勢和導水率均產生影響，因此在凍土情況下 Clapp-Hornberger關系式可推廣寫為（Koren et al., 1999;Jame and Norum, 1980）：

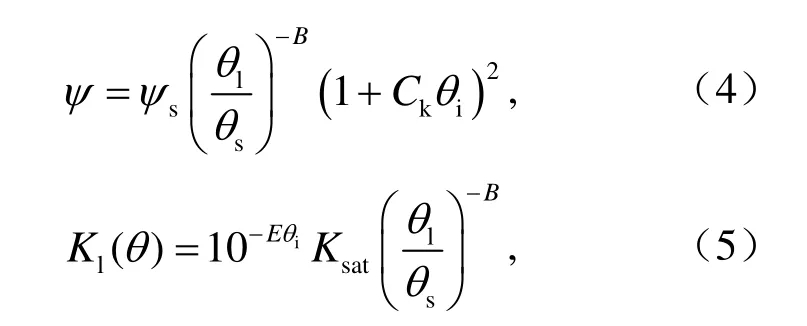
式中，Ck為經驗常數（有一定取值范圍），本文中取為8；E根據Shoop and Bigl（1997）提出的與飽和導水率有關的經驗關系式而定。

因此可見，當土壤質地在垂直方向上有改變、呈現明顯的非均勻性時，相應的土壤水分特征曲線中的與土壤質地有關的參數（如Ksat,ψs,θs，B，Ck和E等）都會有所不同。在這里需要指出的是，目前很多陸面過程模型（Engelmark and Svensson，1993；Koren et al., 1999；M?lders and Walsh，2004）中將（2）式改寫為

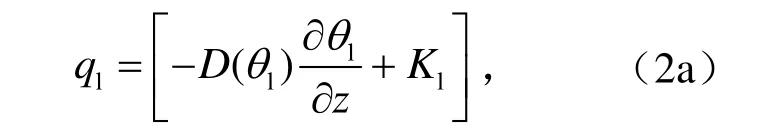
D(θl) 為非飽和土壤水分擴散率（m s-2），且D=Kl(?ψ?θl)，即僅用土壤水分梯度來表征非飽和土壤液態水流動。應該說，在均勻、非凍結土中，土壤水勢和土壤含水量均連續變化、且變化方向相同，方程（2a）能合理地描述液態水流動速率的變化情況。但是在非均勻土或凍土中，土壤水勢應是空間分布連續的，而含水量在不同土壤質地的交界面處會不連續，發生跳躍，且水勢增（減）的方向與含水量增（減）方向有可能不一致，因此由方程（2）決定的水流方向也許與土壤濕度降低的方向相反，所以由含水量梯度決定［即由方程（2a）決定］的水流動并不能正確地反應土壤液態水的流動。且從關系式（4）中可以看出，非均勻土壤中，土壤水勢不僅僅與土壤液態水含量有關，當土壤凍結時還與含冰量有關，與影響土壤質地的土壤飽和水勢及參數B等一起都會對土壤水勢有很大影響。因此如果要用土壤水分擴散率來表征非飽和土壤中液態水流動時，關系式（2）應寫為

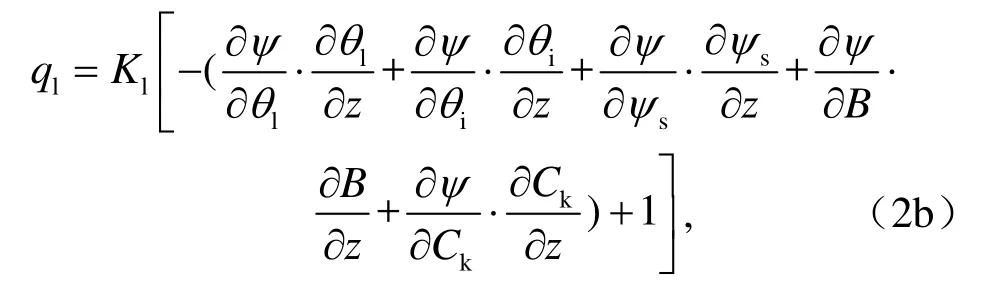
為了簡化，可將方程（2b）寫為

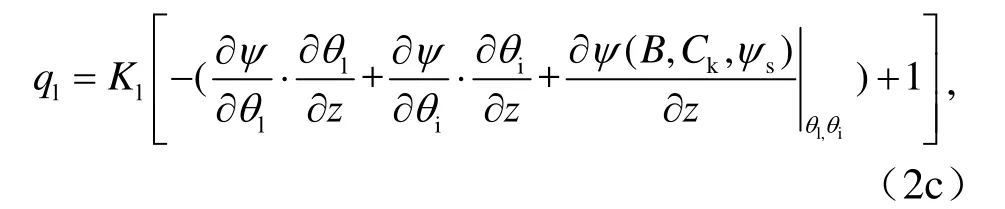
式（2c）中的第一項表示了由于土壤液態水含量的梯度引起的水分流動；第二項表示由于含冰量在垂直方向上的不均勻對水勢影響而造成的液態水流動；第三項表征在液態水含量和含冰量一定的情況下，由于土壤本身質地的不同（B、Ck、ψs的不同）而引起的非均勻性對液態水流動的影響。因此推廣的Darcy定律中描述土壤水分的垂直運動并不是簡單的 ?ψ?z=(?ψ?θl) · (?θl?Z)。所以，在陸面 過程模式中考慮到非均質土和凍土的情況，描述 的液態水流動只能或是直接采用土壤水勢梯度(?[ ?ZKl·(?ψ?Z) ]) 或是采用展開式（2b）才是合理的，但從模型簡潔和應用的角度來說，采用土壤水勢梯度的表達更合理。

2.3 Clapp-Hornberger 關系式中各參數對土壤水力特性的影響

表征非飽和土壤的水分特征曲線關系式（4）、（5）中，影響水分特征曲線的參數包括Ksat,ψs,θs,B,Ck和E等。鑒于Zhang et al.（2007）已經對Ck和E對凍融土壤水熱輸送影響有過相關研究，在這里就不再贅述。仔細觀察后發現，參數B是通過指數形式對土壤水力特性進行影響的。因此這里主要以參數B為例，定量地描述參數B對于土壤水勢和導水率的影響，我們探討了在不同的土壤濕度情況下，土壤水勢和土壤導水率隨參數B的變化情況。

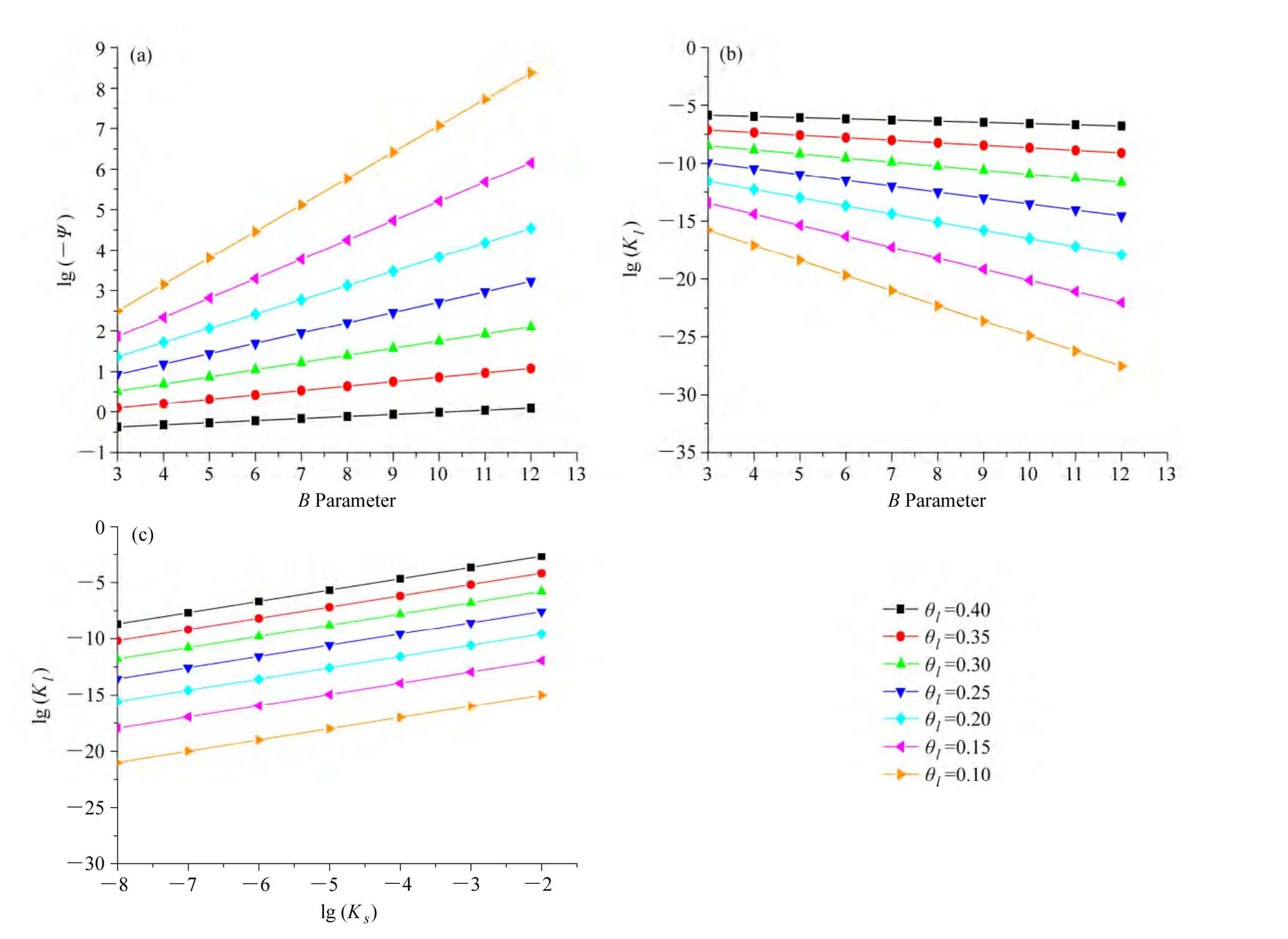
圖1 （a）土壤水勢絕對值的對數（lg(-ψ)）與參數B的關系（ θτ = 0 .40，θs= 0 .45，ψ s =-0 .3）；（b）土壤導水率的對數（ lg (Kl)）與參數B的關系（ θ = 0 .40，θ= 0 .45， K = 4 × 1 0 -6）；（c）土壤導水率的對數（ lg (K)）與飽和導水率的對數（ lg (K)）的關系（ θ= 0 .40，θ= 0.45，B=5）τ ssat ls τ sFig. 1 (a) The relationship between lg(-ψ) and parameter B (θ τ = 0 .40,θs = 0 .45,ψs =-0 .3); (b) the relationship between lg(Kl)and parameter B(θ= 0 .40,θ= 0 .45, K = 4 × 1 0 -6); (c) the relationship between l g(K) and l g(K)(θ= 0 .40,θ= 0 .45,B=5) τ s sat ls τ s

圖1 a中顯示了當土壤總含水量（τθ）為0.4，孔隙度（sθ）為0.45時，不同的液態水含量情況下，土壤水勢絕對值的對數（lg(-ψ)）隨著參數B的變化而變化的情況。可看出，隨著B的不斷增大，土壤水勢絕對值均有所增加。但是，較干的或含冰量越多的土壤水勢絕對值的增幅明顯要高于較濕潤或者含冰量較少的土壤。同時也意味著，在同一含水量情況下，粘土（B=11.4）比砂土（B=4.05）的土壤水勢的絕對值要大。對于土壤導水率來說，隨著B的增加，導水率是下降的（圖1b）。且對于較干的或者凍結程度較深的土壤，其隨著B增加而下降的趨勢比濕潤或未凍結的土壤更明顯。并且當B越大，導水率隨含水量的變化也越大。也就意味著，粘土的導水率明顯低于砂土，且當土壤質地偏向粘土或者是粘土時，土壤含水量的變化能引起導水率較大的變化。此外，導水率的變化除了與參數B有關外，飽和導水率也在一定程度上影響了土壤導水率。明顯地，土壤導水率隨著飽和導水率的增大而增大（圖1c）。即在同一含水量情況下，砂土的導水率高于壤土和粘土。

觀察關系式（4）還發現，不同質地土壤的飽和水勢也對土壤水勢有明顯影響。可以清楚地看出，當土壤飽和水勢絕對值越大，土壤水勢的絕對值也越大。即在同一個溫度下，土壤顆粒對于土壤水的吸附力就會增大，需要更低的土壤溫度才能使土壤水開始凍結。因此掌握了基本的土壤性質參數對土壤水分模擬的影響后，在利用陸面過程模型對垂直非均勻性的土壤進行模擬時，就能較為容易地判斷出模型模擬結果的偏差原因，對模型的校驗有一定的幫助。

3 模型及數據簡介

3.1 簡化的統一土壤模型（Simple Unified Soil Model-SUSM）

SUSM是一個基于物理基礎建立的可用于氣候研究的統一土壤模型（Li et al., 2010）。模型中，采用預報變量替換的方法改寫了目前土壤模型中常用的預報方程，即用土壤焓和土壤水總質量分別代替土壤溫度和土壤含水量作為控制方程的預報變量，使之能有效地處理目前土壤模型中有凍土時存在數值解法不穩定或不收斂的問題。且SUSM保留了用方程（2）（即ql=Kl[ - (?ψ?z)+ 1 ]）來刻畫液態水流通量，能很好地描述由土壤質地本身的空間非均勻性，和由空間非均勻的凍結—融化過程引起的土壤水—熱性質的非均勻性對液態水流通量的影響，從而能很好地應對由此引起的土壤中帶有非均勻性特點的水熱傳輸過程的模擬（Li and Sun,2008），模擬出寒冷地區有凍—融過程的土壤溫度、含水量和含冰量變化。

SUSM中每層土壤的質量平衡和能量平衡方程分別為

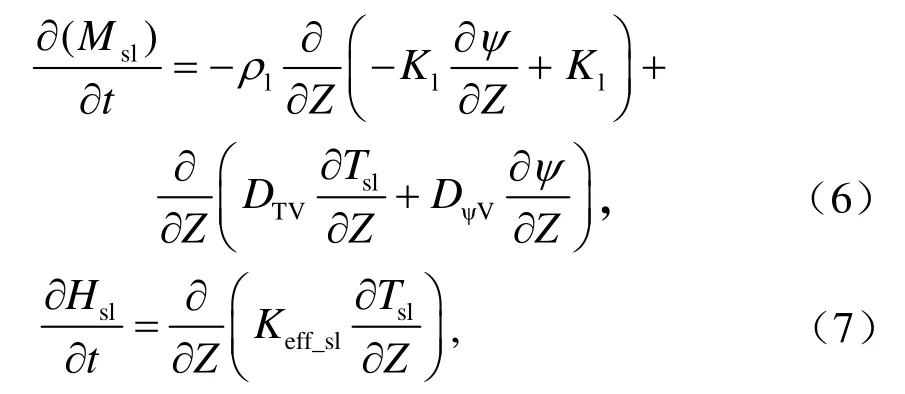
其中，方程（6）為質量平衡方程，Msl為土壤水總質量（為液態水和固態冰的質量之和）（kg m-2）。方程（7）為能量平衡方程，Hsl為土壤總焓（J m-2）（為溫度和含冰量的函數），Keff_sl為土壤有效導熱率（W m-1K-1），Tsl為土壤溫度。方程（6）右邊的第一項代表土壤水分流動對土壤含水量變化的影響，第二項代表土壤中由于溫度梯度和水勢梯度引起的土壤水汽運動對土壤含水量變化的影響。

此外，方程（6）、（7）中有三個未知量（Tsl，θl，θi），要使方程體系完整封閉，還需一個關系式或者限制條件才能決定這三個土壤中的未知量。其中，根據土壤中水—冰—汽三相平衡決定的土壤水勢—冰點的函數關系（稱為冰點水勢方程）：

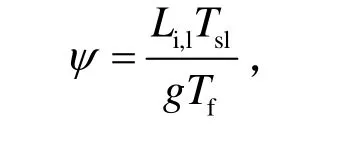
當其與采用的 Clapp-Hornberger關系式（4）聯立后，可得溫度、未凍水含量和含冰量（Tsl，lθ，iθ）三者之間的函數關系：

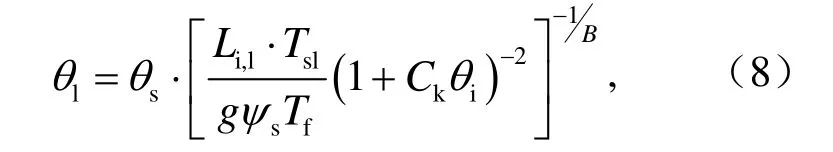
其中，Li,l為融化潛熱，Tsl為土壤溫度（°C），g為重力加速度（m s-2），Tf為273.15 K。Li et al.（2010）分析了目前陸面過程模型中常用的幾類關系式和限制條件后發現，這一關系式是在基于熱力學平衡的基礎上建立起來的，比其他的關系式或者限制條件合理，且采用這個關系式后模型的模擬結果比其他的更加與觀測接近。

針對方程（6）、（7）、（8），Li et al.（2009）發展了相應的有效的數值解法對其進行求解。試驗表明，采用了有效的數值解法的SUSM在運行時更加省時，也更適合于氣候模擬的研究。

3.2 數據簡介

為了研究季風系統中青藏高原陸面過程與大氣的相互作用，從 1996年開始，中日科學家進行了“全球能量水分平衡試驗—青藏高原亞洲季風試驗（GAME-Tibet）”的國際合作項目。在1997～1998年分別進行了第一階段（預試驗）和第二階段（加強觀測）的野外工作，在藏北高原的不同地點分別建立了自動氣象站和埋設了土壤溫度濕度觀測系統，進行相關的觀測。我們選擇了位于青藏公路66道班附近D66站的觀測資料對土壤非均勻性的試驗進行驗證。

D66站位于青藏高原北部（35°31'N，93°47'E），海拔4560 m，屬于大陸性高原氣候，年降水量較少。地表植被稀疏，土壤為非均質永凍土（楊梅學等，2000），最深溫度觀測表明至少有2.6 m的活動層，地下水位2.3 m。D66自動氣象站提供了觀測高度在1.5 m的每30分鐘大氣強迫場資料，包括入射短波輻射通量、氣溫、氣壓、相對濕度和風速。土壤溫度的觀測由 10個白金地溫探頭（Pt）和數采儀獲得，地溫探頭埋設的深度分別為 4、20、40、60、80、100、130、160、200、263 cm。土壤濕度（含水量）的測量由6個時域反射儀（Time-Domain Reflectometer，簡稱TDR）探頭和數采儀完成，TDR探頭的埋設深度分別為4、20、60、100、160、225 cm。土壤的觀測數據每小時自動采集記錄一次。

據分析，D66站的土壤類型主要是砂壤土。D66站土壤類型在垂直方向上還有很大的不均勻性。土壤上部導水率比下部大。此外，很多的研究已表明（Zhang et al., 2007；Li et al., 2010），D66站數據的可靠性有助于研究季節性凍土的水熱輸送變化。因此利用這套資料能對模型針對非均勻性土壤水熱傳輸過程的模擬能力進行驗證。

4 試驗和結果

4.1 SUSM對土壤質地的敏感性試驗

1.3 節中已表明 Clapp-Hornberger關系式中與土壤質地有關的參數（B，sψ，Ks等）對土壤水勢和土壤導水率有較大影響。因此在陸面過程模型中應根據土壤的質地來選取不同的參數才能較為準確地模擬出非飽和土壤中內部的水熱輸運過程。尤其當土壤呈現明顯的垂直非均勻性時，合適的參數選取是模型模擬結果好壞的關鍵。本文中為了說明SUSM模型能較好地反應出土壤質地的垂直非均勻對于土壤水分傳輸的影響，且適用于土壤中垂直非均勻的凍融過程，我們設計了幾個試驗（見表1），利用SUSM在D66站的模擬情況來鑒別模型對土壤質地的敏感性。

表1 不同試驗中簡化的統一土壤模型采用的土壤特性參數Table 1 The parameters for soil texture used by SUSM(Simple Unified Soil Model) in different experiments

三個試驗中用到的土壤參數均已列在表1中。其中控制試驗能使SUSM模型能很好地模擬出土壤內部不同深度的土壤含水量和土壤溫度的變化，包括土壤發生凍結時土壤溫度和含水量的日變化特征。在其他參數不變的情況下，試驗一中的B由控制試驗中的3.86升高到8.86，其主要鑒別模型對于參數B的敏感性。而試驗二用于鑒別模型對于飽和水勢的敏感性，其飽和水勢為-0.881，明顯低于控制試驗的-0.131。由于土壤孔隙度和土壤飽和導水率對于土壤水分的變化較為直觀，且表現上不如參數B和飽和水勢的影響明顯，因此這里只顯示模型對于參數B和飽和水勢的敏感性試驗結果。

從圖2中可看出，控制試驗（黑色實線）基本反映出了由于氣溫的日變化造成的 D66站不同深度的土壤溫度和濕度的日變化特征。4 cm的土壤體積液態水含量由于溫度在0°C上下的日變化而相應地出現日循環波動（圖2b），這與觀測結果非常相符。受到日溫度波的影響，20 cm的溫度在 10月13日以后下降到0°C以下并緩慢降低，出現了明顯的日變化（圖2d），同時土壤出現了緩慢增長的冰，液態水含量也相應減少（圖2c）。60 cm以下的土壤溫度沒有明顯的日變化，只是緩慢降低（圖略）。而試驗一中，B的增大使得模擬出的含水量明顯增大，并且未能體現出含水量的日變化特征（綠色實線）。因為B的增大使得土壤的導水率明顯下降（圖1b），所以土壤水在層與層之間的流動明顯減弱，相對維持一個較高的水平（圖2a，b，c）。即使10月9日的一次降水也只有較少的進入表層以下，其余的作為徑流流走。同時，B的增大也使得土壤水勢的絕對值明顯增加（圖1a），土壤對液態水的吸附力增強，開始凍結的溫度也降低，因此當土壤溫度降到攝氏零度以下后，在4cm和20 cm處，與控制試驗比，即使溫度較低土壤所持有的未凍結水含量也較高（圖2b，c），試驗一中土壤并未發生土壤的凍結。此外，從圖2d中明顯看出在夜間，有結冰過程的控制試驗比未發生凍結的試驗一模擬的土壤溫度高，這主要是由于土壤結冰過程中釋放的凝結潛熱所致。因為這種情況下，此時控制試驗的土壤已經結冰，但試驗一中的土壤并未結冰，土壤溫度因為沒有結冰釋放的潛熱加熱而持續下降，從而在觀測的土壤凍結時期，模擬的土壤溫度振幅偏大。同理，在白天溫度升高后土壤融化需要的熱量會使溫度有所降低，而試驗一中并未能體現出這一土壤內部凍融過程對土壤溫度的影響。

試驗二中土壤水勢絕對值的增加使得土壤開始凍結的溫度也下降，結冰過程較之控制試驗有所延遲（藍色實線）。所以表現出在4 cm及20 cm處土壤液態水含量的日變化特征不如控制試驗的明顯（圖2b，c）。但是僅增加飽和水勢絕對值（試驗二）不如增加B的值（試驗一）對水分和溫度的影響明顯。因為B是通過指數形式影響土壤水勢和導水率的。

以上的試驗可以看出，當土壤未凍結時，參數B越大導水率越小，使得土壤水分在上部的流動性減弱，因此試驗一模擬的土壤水分相對于觀測值及試驗二的模擬值偏高。如圖2b中的綠色實線所示。

同時，參數B越大飽和水勢的絕對值也越大，當溫度降到零攝氏度以下時，土壤凍結的臨界溫度較低，液態水含量明顯也偏高。因此關系式（4）中的參數B的選取對于模型在模擬非凍結和凍結土壤時的表現起到很大作用。

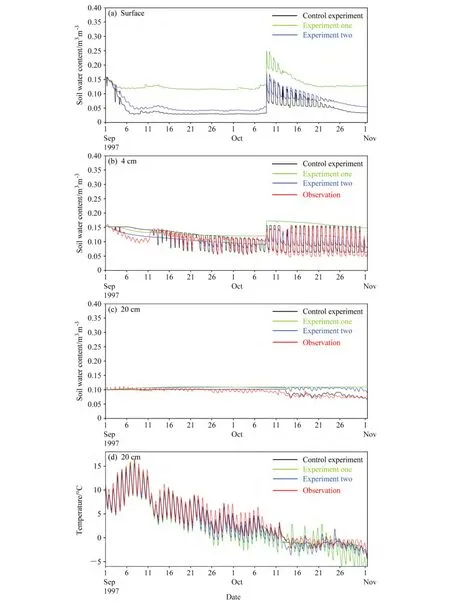
圖2 簡化的統一土壤模型模擬的D66站（a）表面、（b）4 cm、（c）20 cm深度的土壤液態水含量（m3 m-3）和（d）20 cm處土壤溫度（°C）與觀測的比較（紅色實線：觀測；黑色實線：控制試驗；綠色實線：試驗一；藍色實線：試驗二）Fig. 2 Comparison of soil water content (m3 m-3) and soil temperature (°C) at different soil depths at the D66 site between the simulation results and observations: (a) Soil water content at the surface; (b) soil water content at 4 cm; (c) soil water content at 20 cm; (d) soil temperature at 20 cm

同時也看出，SUSM模型在一定程度上能真實地反應出不同質地的土壤中水分和熱量的傳輸，尤其對由凍融過程引起的土壤性質的空間非均勻性的模擬和分析具有很堅實的理論基礎和實際意義。

4.2 SUSM 對垂直非均勻土壤和垂直均勻土壤的模擬對比分析

以上的三個試驗（表1）中，SUSM模型中土壤上下各層采用的參數都是統一的，如表1所示。而實際上，土壤的垂直分布不均勻特征在我國青藏高原等地比較明顯。利用D66站的數據，我們選取了砂土和粘土這兩個對比較明顯的土壤質地類型在垂直方向上進行組合，同時為了對比垂直均勻與非均勻的土壤在水熱傳輸方面的不同，我們設計了以下四組不同的試驗（表2所示）：

表2 SUSM模型模擬的四種不同的土壤垂直分層組合及用到的Clapp-Hornberger關系式中的各參數Table 2 Parameters in the Clapp–Hornberger relationship used for four combinations of soil vertical stratification in SUSM

（一）土壤模型中垂直方向上表現為非均勻性。

組合1：上部（從地表到10 cm深處）為砂土，下部（從10 cm深處到5 m）為粘土；

組合2：上部為粘土，下部為砂土。

（二）土壤模型中垂直方向表現為均一性。

組合 3：上下均為粘土；組合 4：上下均為砂土。

其中，砂土和粘土的Clapp-Hornberger關系式中的各參數均來自于根據 1845個土壤樣本分析得到的具體數值（Tarboton, 2003）（見表2）。與 3.1節不同的是，這里不只是探討模型對于某個參數的敏感性，而是多個參數的共同作用下的模型對于垂直均勻和非均勻土壤的敏感性。

從圖中可以看出，組合1中（藍色實線）上部大、下部小的飽和導水率導致土壤表面及上部的水分往下流，下部的含水量增大（圖3c）。同時，參數B隨著深度的增加而增加，也會導致土壤導水率越往下越小，從而水分出現明顯的上部偏小（圖3a，b），下部明顯偏大的情形（圖3c）。而根據前面的試驗一和試驗二可看出，參數B對導水率的影響會明顯大于飽和導水率對導水率的影響。組合1中飽和水勢的絕對值也是隨著深度的增加而增大，使得土壤開始結冰的臨界溫度越來越低，結冰過程延后，在20 cm處即使土壤溫度到達零攝氏度以下依然沒有結冰。也就意味著模式中的土壤在實際觀測當中應該結冰（融化）時沒有結冰(融化），所以土壤溫度因為沒有結冰（融化）釋放（吸收）的潛熱加熱（冷卻）而持續下降（上升）因此溫度的振幅明顯大于觀測值。

組合2（綠色實線）與組合1在土壤濕度的模擬上完全相反，上部大下部小的參數B，以及上部小下部大的飽和導水率使得土壤導水率隨著深度的增加而增大，因此10 cm以上的土壤含水量均比觀測值偏大。同時上部飽和水勢絕對值較大的粘土其結冰的臨界溫度也偏低，因此即使在4 cm處當溫度小于零攝氏度，且含水量達到0.26都未結冰。而在20 cm處，砂土的飽和水勢絕對值明顯降低，即使含水量較低（約 0.08），土壤依然隨著溫度的日變化而出現凍結和融化現象。這一日時間尺度上出現的上部未結冰而下部有結冰發生的現象可以說是由于土壤在垂直分布上的不均勻性造成的。在目前大部分模型的模擬結果中是很難見到的。也很少有研究關注。在較短的時間尺度上（日尺度），雖然無足夠的觀測事實來證明這一現象的普遍性，但是從理論上來說，由于土壤的垂直非均勻性造成的這一現象應該也是存在的，因為上下部土壤性質本身的差別造成了土壤凍結臨界溫度的差別，那么即使溫度有到零攝氏度以下，且含水量較高，而未達到使之凍結的臨界溫度土壤仍然不會凍結。

所以從上面的分析可以看出，認識到土壤垂直分布的非均勻性以后如何在模型中加以考慮將直接影響到模型模擬的水熱傳輸等過程。

以上分析了模型在模擬上下部不同土壤質地

的含水量和土壤溫度的變化，為了對比其與垂直均勻的土壤的情形，組合 3（黃色實線）試驗和組合4（紫色實線）試驗分別展示了上下均為粘土和上下均為砂土的具體模擬結果。可看出，對于組合 3來說，在上部（圖3a，b）與組合 2（綠色實線）的結果接近，都是土壤含水量由于較低的導水率而偏大。而在下部（圖3c），組合3由于飽和水勢的絕對值較組合2中的較大，土壤凍結的臨界溫度較組合2中的砂土偏低，因此土壤并未結冰，即含水量維持不變。相應地，20 cm處的溫度振幅也明顯偏大。

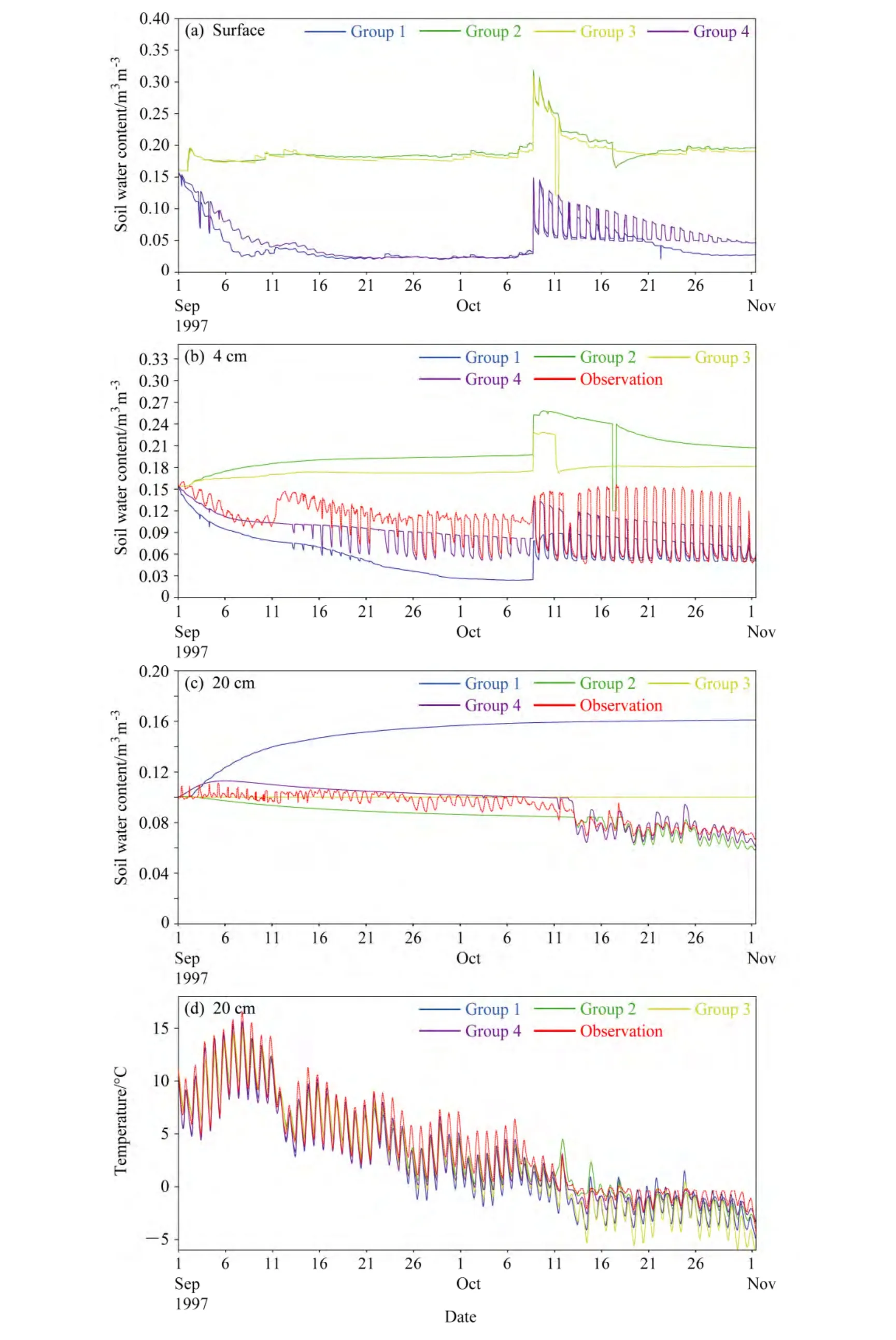
圖3 SUSM模擬的D66站（a）表面、（b）4 cm、（c）20 cm深度的土壤液態水含量（m3 m-3）和（d）20 cm處土壤溫度（oC）與觀測的比較。紅色實線：觀測；藍色實線：組合1；綠色實線：組合2；黃色實線：組合3；紫色實線：組合4Fig. 3 Comparison of soil water content (m3 m-3) and soil temperature (°C) at different soil depths at the D66 site between the simulated results and observations: (a) Soil water content at the surface; (b) soil water content at 4 cm; (c) soil water content at 20 cm; (d) soil temperature at 20 cm

上下均為砂土的組合4較之組合1來說，明顯的差別在4 cm和20 cm處的土壤濕度的模擬上，組合4中下部偏大的導水率使得4 cm和20 cm的含水量分配更為合理，并不像組合2中由于下部小的導水率使得20 cm處偏高。同時，較組合1偏小的飽和水勢絕對值，也使得組合4中的土壤在20 cm處即使含水量不及組合1中的含水量高，也可以有凍融現象發生。此外，從與觀測的對比上看，似乎上下均為砂土的組合4更接近于觀測值，但這并不能完全認為 D66站的土壤實質為上下均一的均勻性土壤。只可以說土壤類型應該是偏砂土類型的，因為這還與模型的分層等有關。

5 結論和討論

本文主要是針對陸面過程模型中非均勻土壤的濕度模擬進行理論分析和敏感性試驗研究。關于土壤非均勻性的概念，文中不僅考慮土壤質地的垂直非均勻分布，還包括了土壤發生凍結后有冰存在導致的土壤性質的不均勻性。對陸面過程模型中常用的描述非均勻土壤水分垂直流動的推廣的達西定律進行理論分析，指出采用土壤水勢梯度表征水分流動的合理性和優越性，也指出目前常用的部分陸面過程模型中采用土壤含水量梯度表征水分流動不合理性，即可能會出現水分流動沿土壤濕度減小、但水勢增大（水勢絕對值減小）方向的不協調情況。并利用了表征土壤水分特征的經典的 Clapp-Hornberger關系式對土壤水分特性進行了分析。結果表明，關系式中的參數B，飽和水勢及飽和導水率對土壤濕度的模擬起到了關鍵作用。參數B的增加會導致導水率的大大下降。飽和水勢的絕對值和參數B的增加會使得土壤水勢絕對值增加明顯，從而土壤的凍融過程發展的向低溫方向偏移，即在同一溫度、同一總含水當量下，具有較大值的參數B和飽和水勢絕對值的土壤凍結的可能性小，而所含的液態水含量較大。

盡管文中我們重點討論了土壤的非均勻性對土壤水分特征和水分傳輸的影響。實際上，從圖中可以看出，土壤中的溫度和水分是相互作用的。例如，組合1和組合3中的土壤在20 cm處未發生凍結，使得此深度的土壤溫度未受到土壤凍（融）所釋放（吸收）熱量的影響，從而出現了比觀測值振幅偏大的情況。這一現象明顯體現出土壤中的水熱傳輸的相互作用。本文雖主要集中在用 Clapp-Hornberger關系式中用到的各參數來討論土壤非均勻性對水量平衡的影響，實際上，土壤中與熱傳輸緊密相關的土壤導熱率也受到土壤質地的影響。王愚等（2013）的工作曾指出過采用不同的土壤熱傳導方案對青藏高原站點土壤溫度的模擬結果有較大影響。土壤的孔隙度，飽和度和晶粒尺寸分布及礦物質含量等都會對土壤的熱傳導率有影響，當有冰存在時，由于冰的導熱系數是水的4倍，因此土壤中冰的存在又會大大增加土壤的熱傳導率。所以可以看出，土壤濕度和溫度的模擬都應該合適準確地考慮到土壤的垂直非均勻性，并且考慮兩者是相互影響和作用下進行的。

文中的工作僅僅是利用模式對于土壤垂直非均勻性的敏感性試驗來說明土壤性質參數選取的一個重要性，它對于陸面過程模型起到了關鍵作用。但是在實際應用中，如果考慮到不同地區不同深度的土壤質地非均勻性，那么將是一個繁重的工作，對于計算空間和機時等的要求也會比較大。所以在認識到土壤垂直非均勻性的重要性之后，我們可以在模型中選用一個較為理想的替代方法，將某個尺度的非均勻性土壤看作是一個等效的均勻介質或等效簡化的非均勻介質，用一組有效的土壤性質參數來表征這一均勻介質或等效簡化的非均勻介質，以求對這一尺度的土壤平均流做出合適的預報。例如3.1節中所提到的控制試驗，其中所采用的參數并非根據某一類型土壤的具體特性而定，而可以將這個非均勻土壤看作一個等效簡化的均勻介質來對待，所以這一方法就回歸到對某一組有效參數的鑒定上。但是這樣做僅僅是為了計算和應用的方便，并不能真正地忽視土壤垂直非均勻性在水熱傳輸模擬中的重要性。

此外，本研究僅僅利用了一個沒有考慮植被覆蓋的土壤模型，當有植被覆蓋時，植被的根抽吸作用對于土壤水分的影響也應該考慮。

（References）

Brooks R H, Corey A T. 1966. Properties of porous media affecting fluid flow [J]. J. Irrig. and Drain. Div. ASCE, 92: 61–90.

Burdine N T. 1953. Relative permeability calculations from pore size distribution data [J]. Journal of Petroleum Technology, 5 (3): 71–78.

Clapp R B, Hornberger G M. 1978. Empirical equations for some soil hydraulic properties [J]. Water Resour. Res., 14: 601–604.

Destouni G, Sassner M, Jensen K H. 1994. Chloride migration in heterogeneous soil: 2. Stochastic modeling [J]. Water Resour. Res., 30:747–758.

Engelmark H, Svensson U. 1993. Numerical modelling of phase change in freezing and thawing unsaturated soil [J]. Nord. Hydrol., 24: 95–110.

郭維棟, 馬柱國, 王會軍. 2007. 土壤濕度——一個跨季度降水預測中的重要因子及其應用探討 [J]. 氣候與環境研究, 12 (1): 20–28. Guo Weidong, Ma Zhuguo, Wang Huijun. 2007. Soil Moisture—An important factor of seasonal precipitation prediction and its application [J]. Climatic Enviromental Research (in Chinese), 12 (1): 20–28.

Jame Y W, Norum D I. 1980. Heat and mass transfer in a freezing unsaturated porous medium [J]. Water Resour. Res., 16: 811–819.

Jensen K H, Mantoglou A. 1992. Application of stochastic unsaturated flow theory, numerical simulations, and comparisons to field observations [J].Water Resour. Res., 28: 269–284.

Jhorar R K, Dam J C, Bastiaanssen W G M, et al. 2004. Calibration of effective soil hydraulic parameters of heterogeneous soil profiles [J]. J.Hydrol., 285: 233–247.

Koren V, Schaake J, Mitchell K, et al. 1999. A parameterization of snowpack and frozen ground intended for NCEP weather and climate models [J]. J. Geophys. Res., 104: 19569–19585.

Koster R D, Dirmeyer P A, Guo Z, et al. 2004. Regions of strong coupling between soil moisture and precipitation [J]. Science, 305: 1138–1140.

Li Q, Sun S F. 2008. Development of the universal and simplified soil model coupling heat and water transport [J]. Sci. China Ser. D Earth Sci.,51: 88–102.

Li Q, Sun S F, Dai Q D. 2009. The numerical scheme development of a simplified frozen soil model [J]. Adv. Atmos. Sci., 26: 940–950.

Li Q, Sun S F, Xue Y K. 2010. Analyses and development of a hierarchy of frozen soil models for cold region study [J]. J. Geophys. Res., 115,doi:10.1029/2009JD012530.

Mahmood R, Hubbard K G. 2003. Simulating sensitivity of soil moisture and evapotranspiration under heterogeneous soils and land uses [J]. J.Hydrol., 280: 72–90.

Mantoglou A. 1992. A theoretical approach for modeling unsaturated flow in spatially variable soils: Effective flow models in finite domains and nonstationarity [J]. Water Resour. Res., 28: 257–267.

M?lders N, Walsh J E. 2004. Atmospheric response to soil-frost and snow in Alaska in March [J]. Theor. Appl. Climatol., 77: 77–105.

Rind D. 1982. The influence of ground moisture conditions in North America on summer climate as modeled in the GISS GCM [J]. Mon. Wea.Rev., 110: 1487–1494.

Sassner M, Jensen K H, Destouni G. 1994. Chloride migration in heterogeneous soil: 1. Experimental methodology and results [J]. Water Resour. Res., 30: 735–746.

Shoop S A, Bigl S R. 1997. Moisture migration during freeze and thaw of unsaturated soils: Modeling and large scale experiments [J]. Cold Reg.Sci. Technol., 25: 33–45.

Shukla J, Mintz Y. 1982. Influence of land-surface evapotranspiration on the Earth’s climate [J]. Science, 215: 1498–1501.

Tarboton D G. 2003. Rainfall-Runoff Processes [R]. Workbook, Utah State University.

van Genuchten M T. 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Sci. Soc., 44:892–898.

王愚, 胡澤勇, 荀學義, 等. 2013. 藏北高原土壤熱傳導率參數化方案的優化和檢驗 [J]. 高原氣象, 32: 645–653. Wang Yu, Hu Zeyong, Xun Xueyi, et al. 2013. Optimization and test of soil thermal conductivity parameterization schemes in northern Qinghai–Xizang Plateau [J].Plateau Meteor. (in Chinese), 32: 645–653.

楊梅學, 姚檀棟, 勾曉華. 2000. 青藏公路沿線土壤的凍融過程及水熱分布特征 [J]. 自然科學進展, 10: 443–450. Yang Meixue, Yao Tandong, Gou Xiaohua. 2000. Soil freezing and thawing process and its hydrothermal distribution along the Qinghai–Tibet highway [J]. Progress in Natural Science (in Chinese), 10: 443–450.

Yeh T C, Harvey D J. 1990. Effective unsaturated hydraulic conductivity of layered sands [J]. Water Resour. Res., 26: 1271–1279.

Yeh T C, Wetherald R T, Manabe S. 1984. The effect of soil moisture on the short-term climate and hydrology change—A numerical experiment [J].Mon. Wea. Rev., 112: 474–490.

Yeh T C, Gelhar L W, Gutjahr A L. 1985a. Stochastic analysis of unsaturated flow in heterogeneous soils: 1. Statistically isotropic media[J]. Water Resour. Res., 21: 447–456.

Yeh T C, Gelhar L W, Gutjahr A L. 1985b. Stochastic analysis of unsaturated flow in heterogeneous soils: 2. Statistically anisotropic media with variable α [J]. Water Resour. Res., 21: 457–464.

張述文, 李得勤, 邱崇踐. 2009. 三類陸面模式模擬土壤濕度廓線的對比研究 [J]. 高原氣象, 28: 988–996. Zhang Shuwen, Li Deqin, Qiu Chongjian. 2009. A comparative study of the three land surface models in simulating the soil moisture profile [J]. Plateau Meteor. (in Chinese), 28:988–996.

Zhang X, Sun S F, Xue Y K. 2007. Development and testing of a frozen soil parameterization for cold region studies [J]. J. Hydrometeor., 8 (4): 690–701.