OSEM 重建算法及其改進算法的研究和比較

楊 娟，王明泉，石 浪，侯慧玲

（中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原030051）

0 引 言

最大似然期望值最大算法 （MLEM）是一種基于統計的迭代重建算法，該算法對噪聲有較強的抑制作用，但因其計算量大，收斂速度慢，在實際當中的應用較少。Hudson等將有序子集 （ordered subsets of projection data）應用到MLEM 算法中，簡稱OSEM。OSEM 算法將投影數據按投影角度分解成有限個有序子集，每個子集應用MLEM 算法對圖像更新一次，為一次子迭代，所有的子集全部使用完，為一次完整的迭代。相對于MLEM 算法，OSEM 算法在一次迭代過程中，重建圖像更新了n次，因此加快了圖像的收斂速度［1，2］。

OSEM 算法子集水平的不同會對重建圖像的收斂速度以及重建圖像的質量產生不同的影響。如何選取子集才能使重建結果最優，許多學者對OSEM 算法做出了不同的改進。Kadrmas提出了統計自適應EM 算法 （StatREM）［3］，該算法利用投影數據的統計信息，通過檢驗統計量，在每次迭代時自動調整子集數目，但其統計過程比較復雜；孔慧華等將MOS－BR算法應用到OSEM 算法中，提出了子集序列EM 算法 （SSEM）［4，5］，該算法提前將子集水平設為一個單調不增序列，每次迭代順序使用序列中的子集數，但其子集序列的選擇還要視重建結果予以調整；Vaissier提出了CROSEM （Count－Regulated OSEM）算法［6］，該算法只需設定子集水平為最大值，重建過程中，根據每個像素的活度大小，對其進行更新。該算法有效地改善了OSEM 算法重建SPECT 圖像時低頻元素丟失的問題［7］。

本文首先研究了OSEM 算法子集的不同選取對重建結果的不同影響，然后分析了SSEM 算法和CROSEM 算法的原理，最后分別使用OSEM 算法、SSEM 算法和CROSEM算法完成對Sheep＿Logan模型和固體火箭發動機模型的重建，對比重建圖像的收斂速度、重建圖像的質量，分析3種算法的實用性和有效性。

1 OSEM 算法

1.1 OSEM 算法簡介

設定重建圖像大小為n×n，360 個投影角度，每個角度下n條投影射線。將投影數據按投影角度劃分成T 個有序子集。OSEM 算法的迭代公式如下

式中：x——待重建圖像，pi——第i條射線的投影數據，wij——第i條射線穿過第j個像素的長度，Sl——第l個子集，l＝1，2，...，T。

1.2 子集水平對重建結果的影響

OSEM 算法重建圖像過程中，子集水平較大時，圖像先恢復高頻元素信息，子集水平較小時，圖像先恢復低頻元素信息。并且，當投影數據不含噪聲時，子集水平越大，重建圖像的收斂速度越快；子集水平越小，圖像的收斂速度越慢。但是一般CT 設備的投影數據都含有泊松噪聲，此時，使用OSEM 算法進行重建，子集水平越大，圖像收斂速度依舊比較快，但是隨著迭代次數的增加，圖像會發散，而子集水平越小，圖像收斂速度越慢，并且圖像的高頻元素信息會丟失［8］。

2 SSEM 算法

為了改善OSEM 算法子集水平對重建圖像的收斂速度以及重建圖像的質量的影響，孔慧華基于MOS－BR 算法，對OSEM 算法做出改進，提出了子集序列EM 算法 （subset sequence EM），簡稱SSEM。

SSEM 算法對OSEM 算法的改進之處在于：SSEM 算法的子集水平不是一個固定值，而是一個單調不增序列。在迭代重建過程中，先使用大的子集水平，恢復圖像的高頻元素，加快重建圖像的收斂速度，然后在下一次迭代時降低子集水平，恢復圖像的低頻元素，避免重建圖像的發散。如此循環，到子集序列結束。

這樣，在重建過程中，先恢復高頻元素，再恢復低頻元素，既加快了重建圖像的收斂速度，又避免了重建圖像的發散。

SSEM 算法子集序列的不同也會對重建圖像的收斂速度以及重建圖像的質量產生影響。一般序列中的第一個子集水平要不大于投影角度數，大小相同的子集水平的個數還要具體視重建結果予以調整［9］。

3 CROSEM 算法

OSEM 算法重建SPECT 圖像時，子集水平選擇越大，在重建過程中，低活度像素的灰度值會被更新為0，導致這些像素信息的丟失。而子集水平選擇越小，圖像的收斂速度越慢，隨著迭代次數的增加，低活度像素的灰度值仍然會被更新為0，導致信息的丟失［10－12］。

為此，Vaissier提出了CROSEM （count－regulated OSEM）算法，該算法與OSEM 算法的不同之處在于：OSEM算法每次迭代更新圖像，都是對圖像的每一個像素值進行修正；而CROSEM 算法在迭代更新圖像時，需要判斷每一個像素的活度是否大于一個設定的閾值CTV （count threshold value），如果大于，這個像素值才會被更新，否則，不予更新。并且，CROSEM 算法的子集水平是其取值范圍內的較大值，如此可以加快重建圖像的收斂速度。

將CROSEM 算法應用到CT 圖像重建，其重建步驟是：

（1）使用MLEM 算法，迭代一次重建圖像。根據重建圖像估計每個像素的活度，確定閾值CTV；

（2）k＝0，并給定正的初值圖像x（0），指定迭代次數Niter，指定子集水平NS等于或小于投影角度數；

（3）進入子集Sl運算，計算下列參數

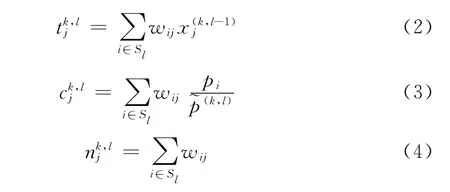
（4）根據第三步的結果，計算下列參數

重復步驟 （3）、步驟 （4），直到k＝Niter。

CROSEM 算法根據每個像素的活度來更新圖像，解決了子集水平過高時，低活度像素丟失的問題，并且，其子集水平為取值范圍內的較大值，加快了重建圖像的收斂速度［9－11］。

4 實驗結果及分析

為了對比3種算法的有效性和實用性，分別使用3種算法對Sheep＿Logan頭部仿真模型和實際的固體火箭發動機模型進行重建，并采用歸一化均方距離對重建結果進行評價，其表達式如式 （8）所示

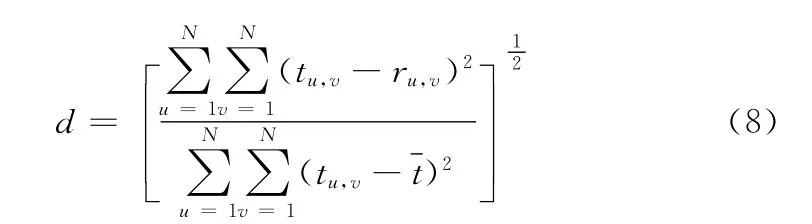
式中：tu，v，ru，v——原始圖像和重建圖像中各像素的灰度值。珋t——原始圖像灰度的平均值。d 值越小表示重建圖像與原始圖像的偏差越小，重建圖像的質量越好。

重建Sheep＿Logan頭部模型，重建圖像大小為256×256，投影角度是將360°均分為256份，每個投影角度下有256條投影射線。OSEM 算法選定子集為64，迭代5 次；SSEM 算法選定的子集序列為256→128→64→32→32；CROSEM 算法的子集為最大值256，迭代5次。原始圖像及其第128行的灰度曲線如圖1所示，3種算法的重建圖像及其第128行的灰度曲線分別如圖2、圖3、圖4所示。

圖1 原始圖像及灰度曲線

3種算法重建圖像的歸一化均方距離d 見表1。

對實際采集的投影數據進行重建，實驗參數為：射線源電壓為290KV，電流為1.8mA。探測器大小為1920×1536，探元大小為0.127mm，射線源到旋轉中心的距離為1060mm，旋轉中心到探測器的距離為140mm，工件旋轉一周，采樣間隔為1 度。設定重建圖像大小為256×256。OSEM 算法選定子集水平為36，迭代3次，其重建結果如圖5所示。

表1 3種算法重建圖像的歸一化均方距離

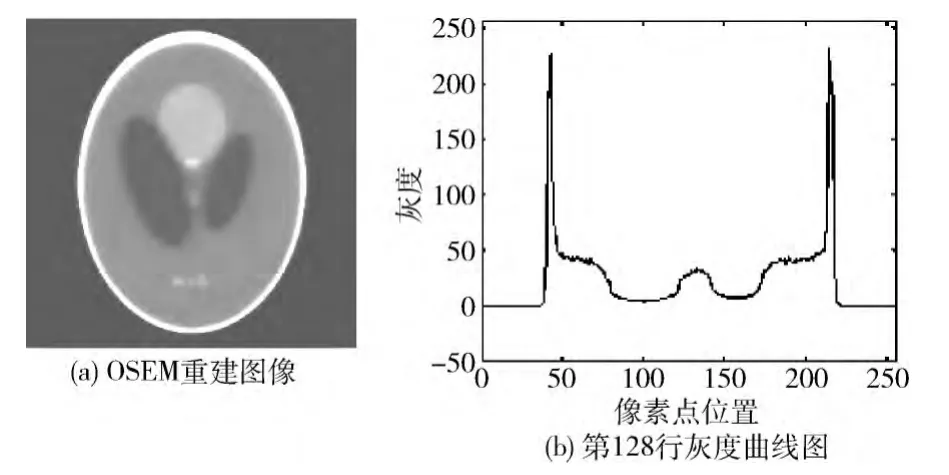
圖2 OSEM 重建圖像及灰度曲線

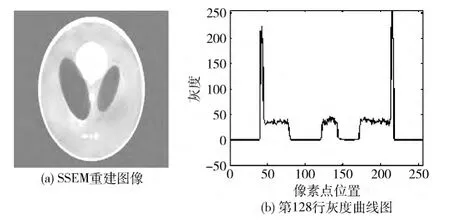
圖3 SSEM 重建圖像及灰度曲線

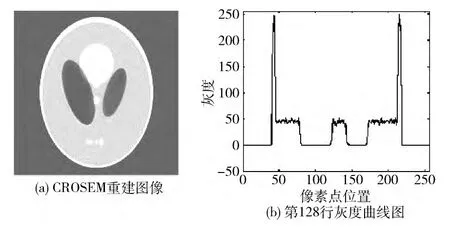
圖4 CROSEM 重建圖像及灰度曲線

圖5 OSEM 算法重建圖像

SSEM 算法，選定子集序列為90→90→60→60→30，其重建結果如圖6所示。

CROSEM 算法，設定子集水平為90，迭代5次，其重建結果如圖7所示。

圖6 SSEM 算法重建圖像

圖7 CROSEM 算法重建圖像

對比3種算法重建的結果以及表1所示的歸一化均方距離，可知：

（1）算法的收斂速度：3種算法相同的迭代次數，所得重建圖像的歸一化均方距離關系為：CROSEM＜SSEM＜OSEM，因此，CROSEM 的收斂速度優于SSEM，SSEM優于OSEM；

（2）重建圖像的質量：CROSEM 優于SSEM，SSEM優于OSEM；

（3）子集選擇的不定性：CROSEM 算法的子集水平為其取值范圍內的較大值，而OSEM 算法與SSEM 算法的子集水平，都要根據重建結果來不斷的調整，因此，CROSEM 算法更有實用性。

5 結束語

OSEM 算法子集的使用加快了MLEM 算法的收斂速度，但是OSEM 算法子集水平選擇較高時，重建圖像收斂速度快，但隨著迭代次數增加，重建圖像會發散；而子集水平較低時，重建圖像的收斂速度又會變慢，而且，圖像的高頻信息會丟失。因此，子集水平的選取對重建圖像的收斂速度以及重建圖像的質量有很大的影響。SSEM 算法設定子集水平為一個單調不增序列，解決了OSEM 算法子集水平帶來的問題。但是SSEM 算法子集序列的選取，還要視重建結果予以調整。而CROSEM 算法只需設定子集水平為一個固定值，在重建過程中，根據每個像素的活度對圖像進行更新，有效地解決了低活度像素丟失的問題。

最后，對比3種算法對Sheep＿Logan頭部仿真模型和實際固體火箭發動機模型的重建圖像的收斂速度以及重建圖像的質量，驗證了CROSEM 算法的收斂速度更快，重建質量更好，有更好的實用性。

［1］SUN Shousi，QIU Jun，GUI Zhiguo，et al.The EM iterative imaging on the discrete reconstruction points ［J］.Journal of North University of China（Natural of Science Edition），2014，35 （2）：209－217 （in Chinese）.［孫守思，邱鈞，桂志國，等.重建點模型的EM 迭代成像 ［J］.中北大學學報：自然科學版，2014，35 （2）：209－217.］

［2］QUE Jiemin，WANG Yanfang，SUN Cuili，et al.Comparison of four iterative algorithm based on incomplete projection reconstruction ［J］.CT Theory and Applications，2012，21 （2）：169－178 （in Chinese）.［闕介民，王燕芳，孫翠麗，等.基于不完備投影數據重建的四種迭代算法比較研究 ［J］.CT 理論與應用研究，2012，21 （2）：169－178.］

［3］KONG Huihua，PAN Jinxiao.Statistical self－adaptive ordered subsets algorithm for image reconstruction ［J］.Journal of North University of China（National of Science Edition），2010，31 （1）：79－83 （in Chinese）.［孔慧華，潘晉孝.圖像重建的統計自適應子集算法 ［J］.中北大學學報：自然科學版，2010，31 （1）：79－83.］

［4］KONG Huihua.Research on iterative algorithms to speed image reconstruction ［D］.Taiyuan：North University of China Press，2006：32－47 （in Chinese）.［孔慧華.加速圖像重建的迭代算法研究 ［D］.太原：中北大學出版社，2006：32－47.］

［5］KONG Huihua，PAN Jinxiao，WU Kun.Three dimensional OSEM image reconstruction algorithm based optimizing subset order ［J］.Journal of Test and Measurement Thchnology，2011，25 （2）：169－171 （in Chinese）. ［孔慧華，潘晉孝，吳琨.基于優化子集順序的三維OSEM 圖像重建算法 ［J］.測試技術學報，2011，25 （2）：169－171.］

［6］Vaissier PEB，Goorden MC，Taylor AB，et al.Count－regulated OSEM reconstruction ［C］／／IEEE Nuclear Science Symposium and Medical Imaging Conference Record，2012：3315－3320.

［7］ZHANG Xuezhu，QI Yujin.Research on fully 3Dimage reconstruction of pinhole SPECT imaging ［J］.Chinese Science Bulletin，2010，55 （18）：1846－1855 （in Chinese）.［張雪竹，漆玉金.針孔SPECT 成像完全三維圖像重建的研究 ［J］.科學通報，2010，55 （18）：1846－1855.］

［8］JI Dongjiang.Research on iterative reconstruction algorithms of 3D cone beam CT ［D］.Chongqing：Chongqing University Press，2008：18－21（in Chinese）.［冀東江.三維錐束CT 迭代重建算法研究［D］.重慶：重慶大學出版社，2008：18－21.］

［9］KONG Huihua，PAN Jinxiao.An sequence subsets simultaneous algebraic reconstruction techniques［J］.CT Theory and Applications，2008，17 （2）：42－47 （in Chinese）. ［孔慧華，潘晉孝.序列子集聯合代數重建技術 ［J］.CT 理論與應用研究，2008，17 （2）：42－47.］

［10］ZHANG Quan，FU Xuejing，LI Xiaohong，et al.High quality ordered subset expectation maximization reconstruction algorithm，based on multi－resolution for PET images ［J］.Journal of Computer Applications，2013，33 （3）：648－650（in Chinese）. ［張權，付學敬，李曉紅，等.基于多分辨率的PET 圖像優質有序子集最大期望重建算法 ［J］.計算機應用，2013，33 （3）：648－650.］

［11］Zhao Jingwu，Su Weining.An iterative image reconstruction algorithm for SPECT ［J］.Nuclear Science and Techniques，2014，25 （3）：1－5.

［12］LIU Lu.Parallel computing for multi－pinhole SPECT reconstruction algorithm ［D］.Beijing：Tsinghua University Press，2012 （in Chinese）.［劉路.多針孔SPECT 重 建算法并 行實現 ［D］.北京：清華大學出版社，2012.］