基于擴展KMCSP的國際航線運價搜索模型及算法

謝繼文，徐 濤，姜錫珂，李建伏

（1.中國民航大學 計算機科學與技術學院，天津300300；2.中國民航大學 中國民航信息技術科研基地，天津300300；3.民航重慶空管分局 技術保障部，重慶400000）

0 引 言

國際航線運價搜索［1］要解決的問題是在客戶容忍的時間內，在時間和費用等條件約束下，尋找出K 條 “最短路徑”，本質上是一個擴展的K 條多約束最短路徑 （extended K multiple constrained shortest path，EKMCSP）問 題［2］。EKMC－SP問題是在普通K 條多約束最短路徑 （K multiple constrained shortest path，KMCSP）問題的基礎上，將單弧圖模型擴展為多弧圖模型后形成［3］。長期以來，普通KMCSP問題 （屬NP難問題）受到了廣泛的關注和大量的研究，如互聯網中保證服務質量的QoS路由問題是最基本的多約束條件下求K 條最短路徑問題［4］。求解普通KMCSP問題的算法種類繁多，例如IDA＊ ＿MCSP 算法［5］、SAMCRA 算法［6］、隨 機 化 算 法［7］和H ＿MCSP 算 法［8］等，這些算法僅能用來解決K＝1的情形。文獻 ［9］提出的以A＊算法為基礎的A＊Prune算法，致力于尋找K 條最短路徑 （K＝1，2，3…），該算法采用Dijkstra算法做輔助計算，通過不斷搜索和剪枝，直到找出滿足約束的K 條路徑或完成所有路徑搜索為止。

針對國際航線運價搜索中龐大的搜索規模和復雜的圖模型等問題，本文建立了國際航線運價搜索問題的EKMCSP模型并提出了相應的A＊Level算法。該算法結合國際航線運價搜索問題的特點，采用啟發式函數思想和大量剪枝策略來大規模減小搜索空間和提高運算效率。

1 國際航線運價搜索模型

國際航線運價搜索的目的是尋找最能滿足用戶需求的旅行路徑，搜索范圍為整個航線網絡中所有航班，主要約束條件有時間和運價等［10］。運價FARE 定義為兩個城市之間不論有多少航班參與情況下的單程旅行最終花費，其中

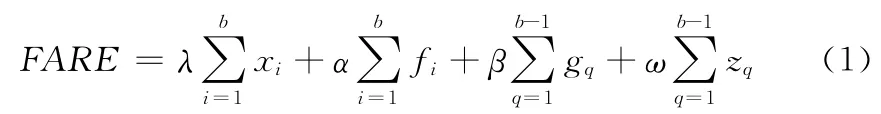
式中：b——起飛城市到目的城市之間的航班數量，xi、fi——第i個航班的飛行時間及票價，gq、zq——第q次中轉的停留時間及金錢花費。FARE 是所求K 條最短路徑排序的依據，當以時間花費為排序的主要依據時，令"＝1，#＝0，$＝1，%＝0；以金錢花費為排序的主要依據時，令"＝0，#＝1，$＝0，%＝1。

國際航線運價搜索的EKMCSP問題與KMCSP問題的差異主要體現在：

（1）圖模型不同。KMCSP問題的圖模型中節點之間僅有一條單向或雙向弧；而在國際航線運價搜索的EKMCSP問題的圖模型中，節點之間可以有多條弧，且弧上權值復雜，包括票價，起降時間和航班號等。

（2）輔助算法不同。求解KMCSP 問題的H ＿MCSP算法和A＊Prune算法等均采用Dijkstra算法進行輔助運算；而國際航線運價搜索的EKMCSP問題因其復雜的圖模型無法使用Dijkstra算法進行輔助運算。

（3）搜索方式不同。KMCSP問題中，可以進行無序或有序搜索；而在國際航線運價搜索中，無論是以最低票價還是以最短旅行時間為目標，旅客轉機次數均是有限的，因此國際航線運價搜索的EKMCSP問題更適合于有限的層次搜索。

1.1 EKMCSP問題的一般描述

令GRA ＝（VR，EG，LI）為一網絡圖，其中VR 為節點集，VR ＝｛vi｜1≤i≤n｝，n為節點數目；EG 為邊集，記eh（vi，vj）為節點vi與vj之間的第h條邊，EG ＝｛eijh｜eijh＝eh（vi，vj），vi，vj∈VR｝；LI 為 所 有 邊 的 權 值 集 合，記l（eijh）為邊eijh的權值，LI＝｛lijh｜lijh＝l（eijh），eijh∈EG｝。假設有起始節點s，目標節點t和約束集CON ＝｛CONi｜i＝1，2，…，R｝，記p（s，t）為s到t的某條可達路徑所經邊的集合，Y（p（s，t））為p（s，t）在約束CON 下的花費，其中

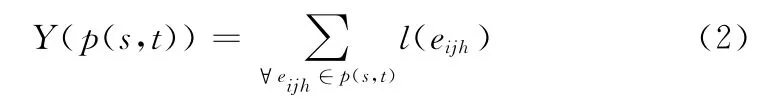
EKMCSP問題即從起始節點s到目標節點t的所有可達路徑中找出K 條最短路徑p（s，t）。

1.2 國際航線運價搜索的EKMCSP模型

國際航線運價搜索問題的EKMCSP模型可以直觀地反映航線網絡的特點。圖1是一個簡單航線網絡的EKMCSP模型圖示例，其中A、B、C、D、E、F 代表6個城市，節點間的每條弧代表執行該航段的一個航班。記MCT ＿TIME為中轉過程中降落航班和起飛航班之間的最小連接時間，BCT＿TIME 表示中轉過程中降落航班和起飛航班之間所允許的最大連接時間，TR 表示可容忍的最大花費，約束條件通常包括：①抵達航班的降落時間與換乘航班的起飛時間之差要大于MCT＿TIME，且小于BCT＿TIME；②已搜索路徑的花費和小于TR；③轉機次數。

針對起始節點到目標節點的可達路徑搜索以樹形層次順序進行。在圖1 中，設起始節點為C，目標節點為B，MCT＿TIME為30分鐘，BCT＿TIME 為120分鐘，轉機次數不超過3次，以C到B的直達航班最高票價作為TR。若任意節點u和d之間存在多弧的情況，則將邊eh（u，d）依次記為udh（h＝1，2，…）。于是，從C 到B 的可達路徑有｛CB1｝，｛CA1，AB1｝，｛CA2，AB1｝，｛CF1，FD1，DB1｝，｛CF2，FD2，DE1，EB2｝等。其中｛CA2，AB1｝不滿足約束條件①，｛CF1，FD1，DB1｝不 滿 足 約 束 條 件②，｛CF2，FD2，DE1，EB2｝不滿足約束條件③。因此在該模型下，運價搜索的結果按照金錢花費多少排序為｛CA1，AB1｝，｛CB1｝。

2 基于EKMCSP模型的搜索算法

國際航線運價搜索的EKMCSP模型中，節點之間存在一條或多條弧，而KMCSP 算法只能解決節點間單弧連接的模型，如A＊Prune算法和約束剪枝算法［11］等。為此針對國際航線運價搜索問題的EKMCSP模型，以A＊算法為基礎，借鑒A＊Prune算法的路徑搜索方式，從初始節點開始搜索，在擴展下一個節點時，不再使用Dijkstra算法進行輔助運算，而是采用路徑價值評估函數的運算結果作為啟發信息。根據這些信息對存儲的路徑集按價值高低進行排序，優先擴展價值較高的路徑。并且在搜索過程中加入有限層搜索的思想，通過不斷的擴展，將生成的新的路徑存儲在價值優先隊列中，利用時間和費用等方面的約束條件對搜索空間進行剪枝，從而形成多約束條件下有限層搜索的A＊算法，簡稱A＊Level算法。

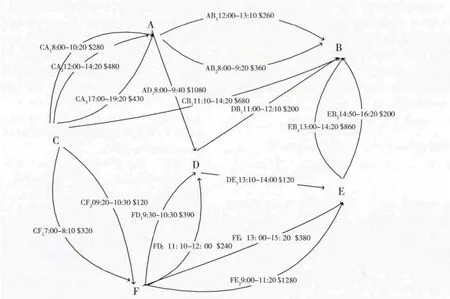
圖1 某航線網絡的EKMCSP模型

2.1 關鍵步驟

2.1.1 數據預處理

對航班屬性等相關數據進行整理并建立相應的數據結構。該數據結構以offairport（起飛機場）為主要標識建立數據塊，數據塊中包含offairport（起飛機場），offcity （起飛城市），inairport（降落機場），incity （降落城市），offtime（起飛時間），intime （降落時間），cost（運價），dep＿longi（起飛機場經度），dep＿lati（起飛機場緯度），arr＿longi（降落機場經度），arr＿lati（降落機場緯度），ct（航班 所 屬 國 家），fltno （航 班 號），onlynumber （唯 一 標識）等信息。所有數據塊以鄰接鏈表形式存儲，并輔助以onlynumber進行定位。

以圖1中的某航線網絡為例，所形成的數據結構如圖2所示。

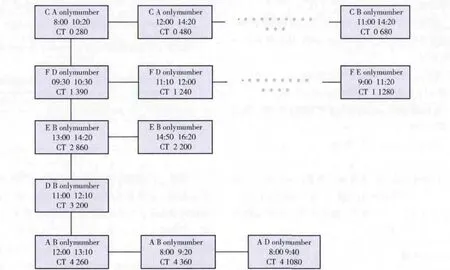
圖2 數據結構

2.1.2 路徑價值評估函數

記任意節點u的地理坐標為（ulongi，ulati），其中ulongi和ulati分別代表節點u的經度和緯度。

設任意節點u和d之間的距離為DISud，則

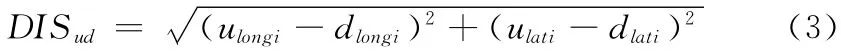
設起始節點s到目標節點t經過節點w，SW（p（s，w））為p（s，w）的路徑和，則

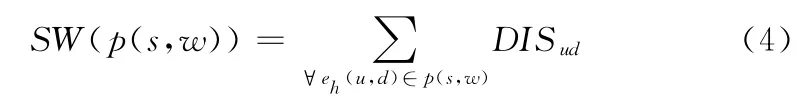
設路徑p（s，w）的價值為VAL（p（s，w）），則

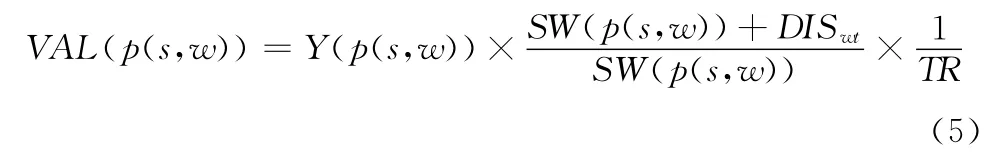
路徑價值評估函數中，綜合考慮了機場地理坐標信息和運價花費等因素，VAL（p（s，w））的值越小，則表示路徑p（s，w）的價值越高。

2.2 算法描述

A＊Level算法的輸入有起飛機場、目的機場、起飛時間和搜索層次等。輸出為起飛機場到目的機場的K 條可達路徑。A＊Level算法的完整描述如下：

步驟1 數據預處理。對航班數據進行整理，并存入特定的數據結構中。

步驟2 初始化。設已找到的路徑數k＝0，并確定TR的值。如果起始節點s和目標節點t之間有直達航班，則以該航班的最高運價為TR；否則從起始節點s開始做兩層搜索，在形成的所有路徑中以花費最多的路徑的運價為TR。從起始節點s開始做一次擴展，形成的所有滿足約束的路徑放入隊列AL＿QUEUE中。

步驟3 隊列排序。對AL＿QUEUE 中所有路徑按其價值從大到小排序。

步驟4 路徑擴展。AL＿QUEUE 隊首的路徑出隊，設該路徑的尾節點為lnode，擴展節點lnode的后繼節點生成若干條新的路徑。

步驟5 剪枝。遍歷擴展生成的所有新的路徑，對產生回路或者不滿足約束條件①、②的路徑進行剪枝。

步驟6 有限層搜索。只在有限層進行路徑擴展，超過限定的層次則進行剪枝。

步驟7 判斷。如果路徑的尾節點即為目標節點，則k＝k＋1。

步驟8 擴充路徑隊列。將擴展后沒有產生回路，且滿足約束條件①、②、③的路徑加入隊列AL＿QUEUE。

步驟9 重復步驟3～步驟8，直到k＝K （目標最短路徑數）或隊列AL＿QUEUE為空。

3 實驗結果及分析

實驗所采用數據集包含網上采集及其它途徑獲得的航班數據，共有12716個國際航班的相關數據。每條航班數據包含offairport，offcity，inairport，incity，offtime，intime，cost，dep＿longi，dep＿lati，arr＿longi，arr＿lati，ct，fltno，onlynumber等字段。設MCT＿TIME 為30 分鐘，BCT＿TIME 為180 分鐘。實驗機器配置：Intel

CoreTM2Duo CPU E4600 2.40GHz，內存2.00GB，操作系統：Microsoft Windows XP Professional 2002Service Pack 3，數據庫：Oracle 9i，編程：Java＋Myelipse＋struts。為驗證基于EKMCSP 模型的A＊Level算法的性能，共設計了3個實驗來進行驗證。

實驗一：設查詢得到的路徑數為K 且為K 條最短路徑，或得到的路徑數小于K 且均為最短路徑，則查詢成功；否則查詢失敗。多組實驗的綜合正確率ACC 為

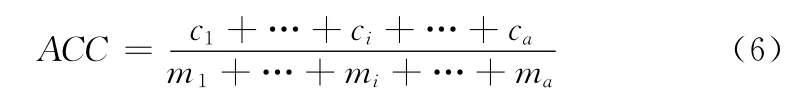
式中：a——進行實驗的組數，mi（1≤i≤a）表示第i組實驗進行的實驗次數，ci——第i組實驗中搜索結果正確的次數。對12716條航班數據進行處理，如果城市間存在多個航班，則只保留一個航班，即將節點間多弧連接的國際航線運價搜索的EKMCSP 模型簡化為節點間單弧連接的KMCSP模型。分別對A＊Level算法和約束剪枝算法進行5組實驗，其中每組實驗5次，每次輸入不同的起飛機場，目的機場，起飛時間和票價類型等。通過實驗后發現，整體上A＊Level算法搜索的正確率和時間效率均高于約束剪枝算法。圖3和表1給出了進行5組實驗的搜索結果。

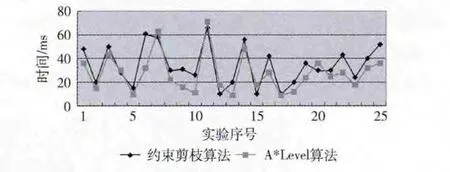
圖3 約束剪枝算法和A＊Level算法的耗時對比

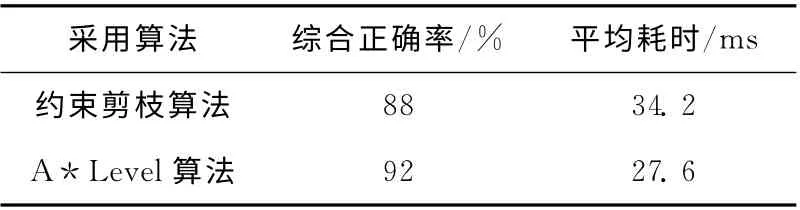
表1 約束剪枝算法和A＊Level算法的效果對比

實驗二：實驗處理的數據對象為12716 個國際航班的相關數據，如果城市間存在多個航班，則保留多個航班，即保持節點間多弧連接的國際航線運價搜索的EKMCSP模型。實驗輸入為：PEK （北京，出發城市），CDG （巴黎，目的城市），2011－01－08 （出發日期），成人 （購票類型）。分別設置4，5和6這3種搜索層次，進行3次實驗。通過實驗后發現，對傳統KMCSP 算法無能為力的國際航線運價搜索的EKMCSP 問題，A＊Level算法可以得到比較滿意的結果。在600ms以內，輸出與搜索層次相對應的最短路徑集，以及每條最短路徑相應的總時間花費和總金錢花費 （見表2）。

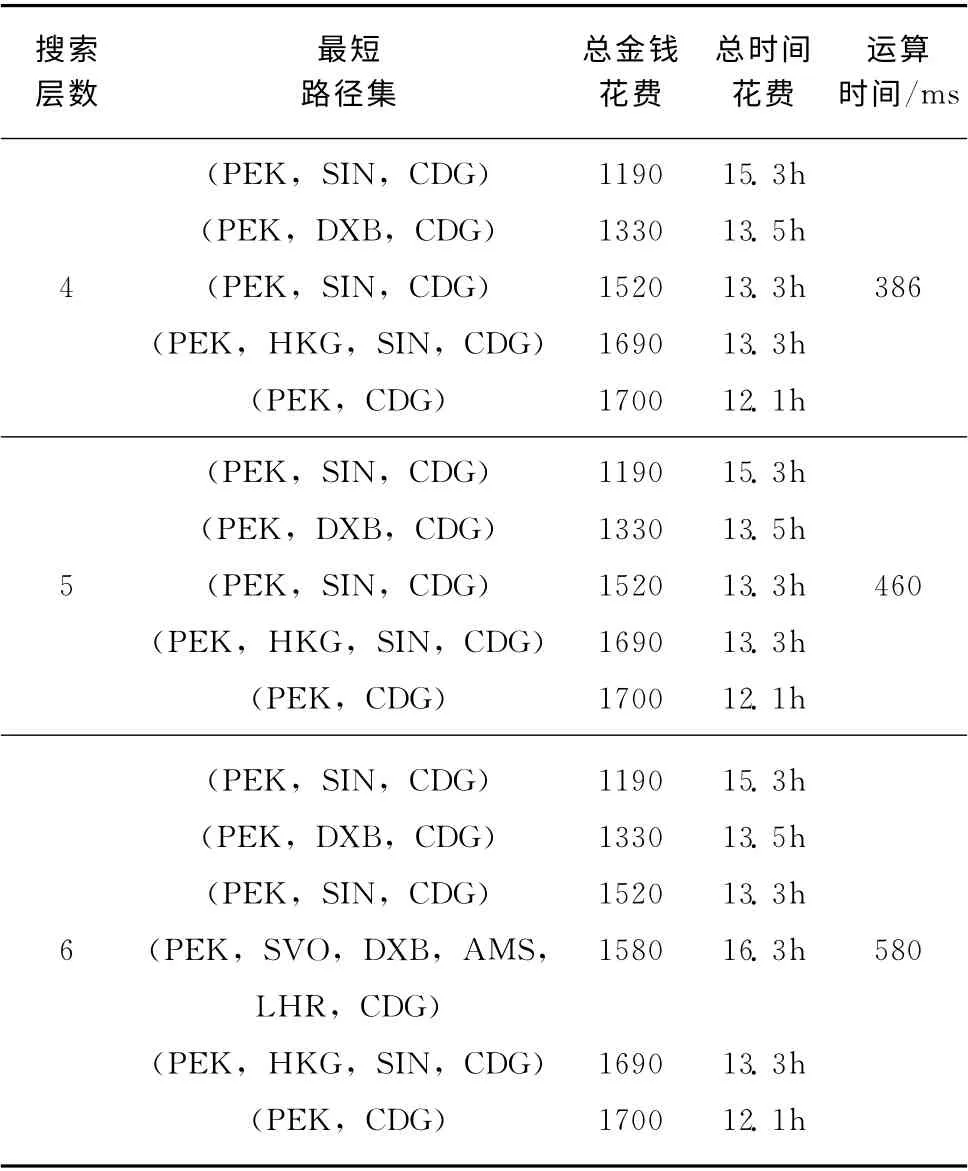
表2 A＊Level算法的輸出結果

實驗三：實驗處理的數據對象為12716 個國際航班的相關數據，如果城市間存在多個航班，則保留多個航班，即保持節點間多弧連接的國際航線運價搜索的EKMCSP模型。表3給出了進行3組實驗的搜索結果，其中每組實驗10次，每次輸入不同的起飛機場，目的機場，起飛時間和票價類型等。

表3 A＊Level算法的正確率驗證

根據式 （4），可得本次實驗的綜合正確率為93.3%。由此可得，A＊Level算法具有較高的正確率。通過3組實驗，證明了A＊Level算法既可以處理節點間存在單弧的模型，也可以處理節點間存在多弧的模型，并具有較優的正確率和時間效率。

4 結束語

目前，國內外對于普通KMCSP問題的應用研究很多，但是針對國際航線運價搜索的EKMCSP問題研究尚少。基于EKMCSP模型的A＊Level算法首先在搜索前進行數據預處理，利用時間、費用等約束條件對搜索空間進行剪枝，并根據民航運輸的特點，采用了有限層搜索的思想。另外，結合機場地理坐標信息和運價花費等因素設計了路徑價值評估函數，以此提高搜索效率。經過驗證，A＊Level算法可以實現國際航線運價搜索的EKMCSP 問題的快速求解，搜索正確率也較高。現實中的全球航線網絡異常復雜，航班數量增加迅速，隨之產生的搜索規模也異常龐大。如何設計更加科學合理的約束條件和更高效率的路徑價值評估函數是下一步研究的重點。

［1］HU Xin，XU Tao，DING Xiaolu，et al.Improvement and simulation of K－shortest－paths algorithm in international flight route network ［J］.Journal of Computer Applications，2014，34 （4）：1192－1195 （in Chinese）. ［胡 欣，徐 濤，丁 曉 璐，等.國際航線網絡中K 條最短路徑算法改進與仿真 ［J］.計算機應用，2014，34 （4）：1192－1195.］

［2］WANG Zhijian，HAN Weiyi，LI Yijun.Shortest path problem with multiple shortest paths［J］.Journal of Harbin Institute of Technology，2010，42 （9）：1428－1431 （in Chinese）.［王志堅，韓偉一，李一軍.具有多條最短路徑的最短路問題［J］.哈爾濱工業大學學報，2010，42 （9）：1428－1431.］

［3］WANG Haimei，ZHOU Xianzhong.Improved shortest path algorithm for restricted searching area［J］.Journal of Nanjing University of Science and Technology （Natural Science），2009，33 （5）：638－642 （in Chinese）.［王海梅，周獻中.一種限制搜索區域的最短路徑改進算法 ［J］.南京理工大學學報（自然科學版），2009，33 （5）：638－642.］

［4］WAN Zhiping，LV Zhimin.A kind of adaptive species optimization of wireless Mesh network Qos routing algorithm ［J］.Journal of Shandong University（Natural Science），2013，48（9）：10－16 （in Chinese）. ［萬智萍，呂志民.一種自適應物種尋優的無線Mesh網絡Qos路由算法 ［J］.山東大學學報（理學版），2013，48 （9）：10－16.］

［5］MA Yueyong，WANG Haimei，LIAO Jianjun.Comparative study of multi－constrained optimal path algorithms ［J］.Journal of Nanjing University of Science and Technology，2011，35（6）：749－754 （in Chinese）. ［馬躍勇，王海梅，廖建軍.多約束最優路徑算法比較研究 ［J］.南京理工大學學報，2011，35 （6）：749－754.］

［6］Zhang Z，Zhao J.Multi－constraint－pru－ning：An algorithm for finding K shortest paths subject to multiple constraints［C］／／Proceedings of APCC，2008：1－5.

［7］ZOU Yonggui，WEI Lai.Optimal path algorithm with multconstrained condition ［J］.Computer Applications，2008，28（5）：1101－1104 （in Chinese）.［鄒永貴，魏來.帶多約束條件的最優路徑選擇算法研究 ［J］.計算機應用，2008，28 （5）：1101－1104.］

［8］NING S.K constrained shortest path problem ［J］.IEEE Transactions on Automation Science and Engineering，2010，7（1）：15－23.

［9］IIT S V，PANDIT A K.A＊prune modified algorithm in video compression ［J］.Ubiquitous Computing and Communication Journal，2008，3 （5）：49－52.

［10］XU Tao，DING Xiaolu，LI Jianfu.Review on K shortest paths algorithms ［J］.Computer Engineering and Design，2013，34 （11）：3900－3906 （in Chinese）. ［徐濤，丁曉璐，李建伏.K 最短路徑算法綜述 ［J］.計算機工程與設計，2013，34 （11）：3900－3906.］

［11］XU Tao，DING Xiaolu，LI Jianfu.K－multiple constrained shortest paths problem for connecting path search in international flight path network ［J］.Journal of Southwest Jiaotong University，2014，49 （1）：153－159（in Chinese）. ［徐濤，丁曉璐，李建伏.國際航線網絡聯程路徑搜索的KMCSP問題研究 ［J］.西南交通大學學報，2014，49 （1）：153－159.］