箱涵結構不同計算模型的精度分析
蒲德龍 李立坤
(1.貴州省交通規劃勘察設計研究院股份有限公司 貴陽 550081; 2.中交二公局第一工程有限公司 武漢 430014)
箱涵結構不同計算模型的精度分析
蒲德龍1李立坤2
(1.貴州省交通規劃勘察設計研究院股份有限公司貴陽550081;2.中交二公局第一工程有限公司武漢430014)
摘要運用結構力學簡化計算及Midas有限元通用軟件,對公路工程中某一常用的通用箱涵結構進行了空間結構受力分析。結果表明,結構力學簡化計算的結果與有限元的計算結果有一定的差距,有限元模型中,用不同單元類型模擬箱涵結構,也存在較大的差別,其中梁單元與板單元的計算結果基本一致,但實體單元的計算結果比其他方法計算的均要小很多;此外,箱涵結構地基支撐剛度也會影響結構的受力;小構件的箱涵結構,結構受力并不是簡單的梁、板單元受力特性,而是一個復雜的空間受力狀況。
關鍵詞公路工程通用箱涵Midas FEA地基剛度
對于公路工程中通用箱涵的受力分析,現行的計算理論主要把空間問題轉化為平面問題,結合結構力學和箱涵計算軟件,對箱涵進行配筋計算和結構驗算。然而,大部分的實際箱涵結構,都是與路線走向有一定的角度,有研究表明[1-2],當斜交角度小于某一個值時,可以不考慮斜交的影響。近些年各大設計院普遍采用斜交轉正交來計算箱涵。當然,對于斜交角度過大的的箱涵,也有其相應的計算理論,那就是通過空間計算結構的彎矩和扭矩,再以主方向上的彎矩和扭矩進行設計配筋。對于這種斜交計算理論,海潮等[3]對其做了研究,王麗等[4]對斜交地道橋的力學特性做了研究,其研究的主要內容是結構的彎矩隨斜交角度的變換情況,對于結構邊界條件支撐剛度的影響等問題并沒有涉獵。目前為止,無論是斜交箱涵還是正交箱涵,做的研究工作,都是在一種計算模式下進行的,并未考慮計算模型的精度,同時,邊界條件均是假定在一個半無限大的彈性體上[5-6],在支撐剛度處理上,支撐剛度對結構受力的影響并沒有做深入的分析。本文對一通用標準箱涵進行多種計算模型下的結構受力分析,得出相關結論,供箱涵結構工程人員參考。
1 工程概況
本合同段為牙同高速公路D標段,項目起點位于青海省海東地區化隆縣哇加灘附近,設計起點樁號為K32+000,路線向南先后跨越S203省道和黃河,再由隆務峽1號長隧道穿越山體,出隧道后,路線終于青海省黃南州尖扎縣當順鄉隆務峽口林業資源管理站附近,終點樁號為K37+000,路線全長5.012km。其中共有13處鋼筋蓋板涵和通道。
選取其中一座箱涵進行結構受力分析,結構尺寸及受力情況見圖1、圖2,設計參數及荷載參數見表1和表2。
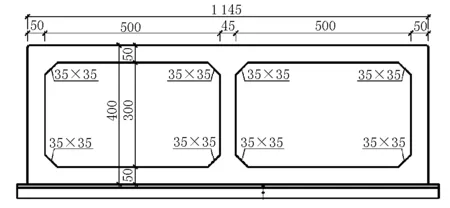
圖1 結構尺寸圖(單位:cm)
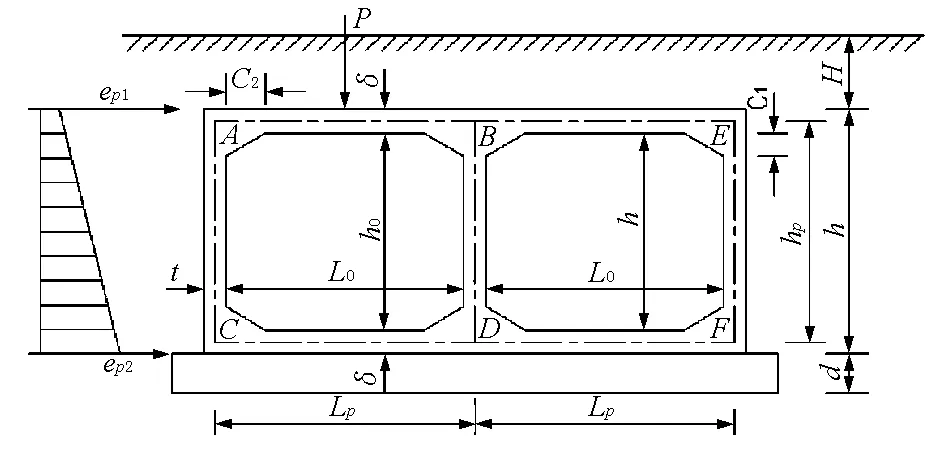

圖2 結構受力簡圖

表2 荷載參數 kPa
2 模型建立及基本假定
本箱涵結構的有限元模型分為平面桿系模型,空間板單元模型以及空間實體單元模型;桿系模型和板單元模型均考慮單元外偏心、無偏心、內偏心3種情況,此外,由于箱涵看作為支撐在半無限體上的空間結構,在荷載或其他作用下,結構是與地基一起發生變形的,故而,本模型考慮了地基支撐剛度對結構受力的影響。
有限元模型基本假定:①箱涵結構底面各點的支撐剛度一致;②不考慮箱涵結構與地基的摩擦作用。實體模型離散圖見圖3。
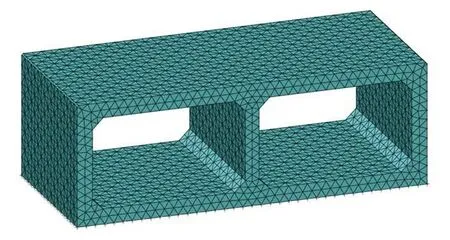
圖3 空間實體模型單元離散圖
3 內力計算及分析
對箱涵中的鋼筋和混凝土進行受力分析,在最不利荷載作用(1.2恒載+1.4活載)下,與結構力學簡化計算所得的內力進行對比,表3~表5為幾種計算方法所得的彎矩內力和應力值。
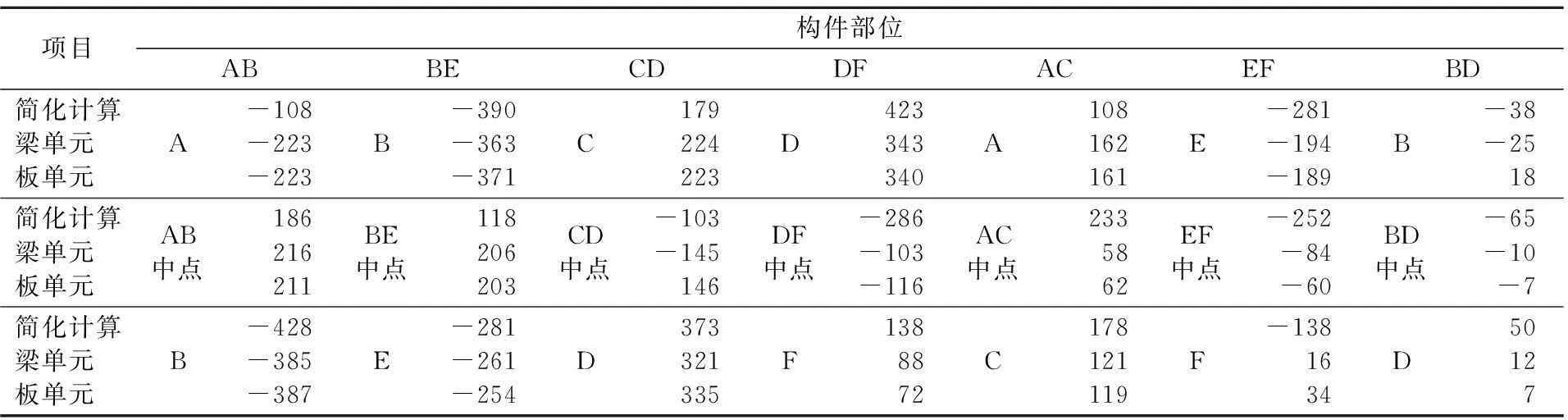
表3 箱涵彎矩內力值比較表 kN·m
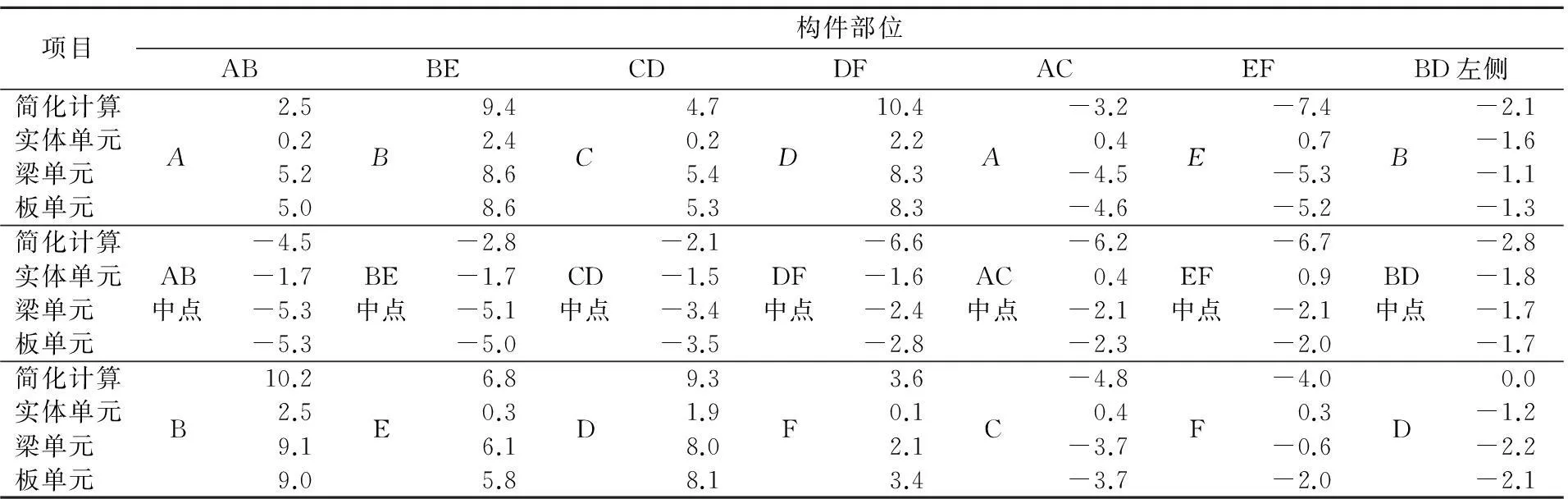
注:構建受壓為正。
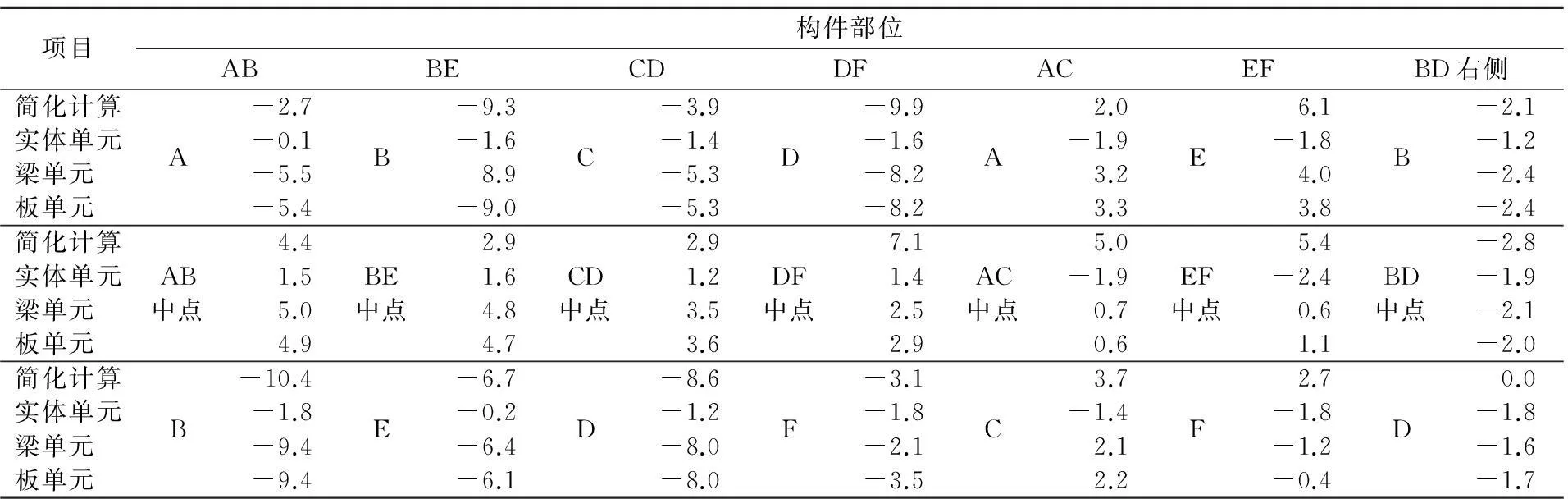
表5 箱涵構件內側應力比較表 MPa
由表3可見,箱涵構件各部分在最不利荷載組合下,簡化計算結果與有限元程序算的結果有一定的差距,箱涵頂板的誤差最大為52%,最小5%;箱涵底板誤差最大為178%,最小11%;箱涵腹板誤差最大為963%,最小33%。而有限元的計算結果,3種方法之間的誤差卻很小,箱涵底板的誤差最大為3%,最小0%;箱涵底板誤差最大為18%,最小0%;箱涵腹板誤差最大為113%,最小0%。從數據變化情況來看,除個別點外,梁、板單元有限元的計算結果,能很好地吻合,而簡化計算與有限元計算之間有很大的差距,特別是腹板的計算;誤差大的原因是除了是由于數據量太小,導致誤差的百分率很大外,另外箱涵簡化計算邊界條件的部分假定,對腹板和底板的受力有很大影響。

圖4 空間實體單元應力圖
從表4、表5,以及圖4的箱涵構件應力計算結果來看,梁、板單元模型的應力值,除腹板和底板的個別點外,大部分關鍵位置的應力值很接近,比如頂板位置以及底板位置都能吻合得好。但實體單元的應力計算結果要遠小于簡化計算和梁、板單元模型的計算結果,部分位置的應力計算結果,簡化計算與梁、板單元模型計算結果能很好地吻合,而與實體單元模型的計算結果有很大的差距,比如BE構件的B位置內側,實體單元模型的應力只有1.6MPa,而其他3種計算方法都在9MPa左右,并且大部分構件的應力值要遠小于簡化計算和梁、板單元模型的計算。
分析原因,對于小構件的箱涵結構,結構受力并不是簡單的梁、板單元受力特性,而是一個復雜的空間受力。對于彎曲平面尺寸大于1/10的構件,截面變形不滿足平截面假定,而梁、板模型均是基于變形協調的平截面假定基礎上進行,使得梁、板模型的計算結果偏大,模擬失真。此外,實體單元底板為一個面的邊界條件,而簡化計算和梁、板單元模型底板的約束情況集中到底板節點上,與實際的受力狀況有一定偏差,對于結構受力不是簡單梁、板單元受力特性的小構件的箱涵來說,這種邊界條件偏差的影響會更大。
4 結論
(1) 構件內力方面,現行的簡化計算結果與有限元的計算結果有一定的差距,并且還與箱涵構件位置有關。
(2) 箱涵邊界條件的假定,對腹板和底板的受力影響要大于頂板,并且把底板的約束情況集中到底板節點上,與實際的受力狀況會有一定偏差。
(3) 箱涵實體空間模型與簡化計算、梁、板單元的平面模型,計算結果有很大的差距,空間實體模型應力值要遠小于平面模型的應力值,說明小構件的箱涵結構,結構受力是一個復雜的空間受力狀況,桿系模型模擬會失真,實體模型模擬相對要可靠。
(4) 按平面桿系計算結果來對箱涵結構進行配筋,箱涵結構的安全系數會很大。
參考文獻
[1]范立礎.橋梁工程[M].北京:人民交通出版社,2001.
[2]林文泉,朱爾玉,田杰.框架式地道橋考慮糾偏內力影響的結構優化設計[J].路基工程,2005(5):4-7.
[3]禹國輝,朱爾玉,李學民.斜交框架箱涵結構在鈍角處的受力和配筋特點[J].北京交通大學學報,37(1):125-127.
[4]王麗,季日臣,伊新芳,等.斜交框架地道橋的力學特性[J].甘肅科學學報,2009,21(1):132-134.
[5]金理平,金明亮.地道橋的有限元法結構分析[J].甘肅科技縱橫,2009,38(1):158-158.
[6]潘文怡.斜交框架地道橋的設計探討[J].鐵道標準設計,2009(6):79-81.
收稿日期:2015-04-11
DOI10.3963/j.issn.1671-7570.2015.04.026

