窄帶雷達觀測下的錐體目標參數估計方法

韓 勛,杜 蘭,劉宏偉

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

窄帶雷達觀測下的錐體目標參數估計方法

韓 勛,杜 蘭,劉宏偉

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

針對現有的基于進動特征的空間錐體目標參數估計假設散射中心微多普勒頻率為正弦與實際情況不符的問題,提出了一種利用窄帶回波中所包含散射中心微多普勒頻率進行參數估計的方法.在建立目標進動模型的基礎上,推導了頂部和底部散射中心理論微多普勒頻率,然后對底部散射中心微多普勒進行展開,并分析了展開系數和目標尺寸與進動參數之間的關系,最后結合頂部與底部散射中心微多普勒建立線性方程組對展開系數進行求解,根據所得展開系數計算了目標尺寸與進動參數.

目標識別;錐體目標;微多普勒頻率;參數估計;特征提取

中段飛行對于彈道防御系統來說十分重要.在這一飛行階段,目標出于保持飛行穩定的需要以及橫向干擾的存在,會出現進動這一特殊的運動形式.進動屬于微運動的一種[1],表現為目標在平動的同時還繞質心小幅轉動.進動可以反映出更多的目標特征,如目標尺寸大小和質量分布等[2-3],這些特征對于真假目標識別是十分重要的,因此利用進動的目標參數估計得到了越來越多的研究.

當目標進動時,被其反射的雷達回波會受到調制,這種調制體現在兩個方面:微距調制與微多普勒頻率調制.微距調制主要是針對寬帶雷達提出的,表現為目標散射中心位置在回波一維距離像序列上周期性變化.微距調制是目標散射中心相對雷達距離發生變化引起的,可以用來對目標尺寸和進動參數進行估計,現有方法也大多是利用一維距離像序列進行參數估計的[4-6].而當雷達發射窄帶信號時,由于帶寬限制,一般無法獲得目標的一維距離像,此時進動引發的調制就表現為微多普勒頻率調制.微多普勒頻率調制的特點是窄帶回波中包含了多個散射中心的瞬時多普勒頻率,反映了進動引發的散射中心相對雷達速度的變化[7-9]. Chen等[10]最早對微多普勒頻率進行研究并推導了不同微動形式對應的理論微多普勒頻率.微多普勒頻率調制相對于微距調制有其優勢所在,體現在對雷達帶寬要求低,同時由于雷達波長短,因此頻率變化更為明顯,更易被提取利用.然而現有工作對基于微多普勒頻率的參數估計研究還不多,且已有的方法一般假設散射中心的微多普勒頻率為正弦,然后利用Hough變化等對正弦曲線進行多維參數提取[11-12].這類方法的缺陷在于:首先,對于錐體目標來說,并不是每個散射中心的微多普勒頻率均為正弦變化,如底部散射中心的微多普勒頻率即較為復雜,不能近似為正弦;其次,即使對于正弦變化的頂部散射中心微多普勒頻率,正弦曲線的幅度也是由多個目標參數共同決定的,僅僅提取曲線參數并不能推得目標參數.因此,基于微多普勒頻率調制的目標參數估計方法還有待進一步研究.

針對上述情況,筆者提出了一種基于微多普勒頻率的錐體目標參數估計方法,對進動狀態下光滑錐體目標表面散射中心的理論微多普勒頻率進行了推導,并根據頂部和底部散射中心的微多普勒頻率關系構建了線性方程組,通過求解方程組系數來對目標參數進行求解,獲得了目標高度、底面半徑、質心位置、進動角及進動頻率等參數.

1 進動目標微多普勒頻率分析

如圖1所示的進動錐體目標,目標高度為H,底面半徑為r,O為目標質心,質心距底面距離OA為h.進動的定義為目標在繞自身對稱軸OZ旋轉的同時還在繞空間定向軸OC旋轉,OZ與OC之間的夾角即進動角為θ;雷達視線（Line of Sight,LoS)與進動軸夾角為γ,γ在短時間內可認為是一個常數.當目標進動時,雷達視線與目標對稱軸夾角β隨時間變化,即

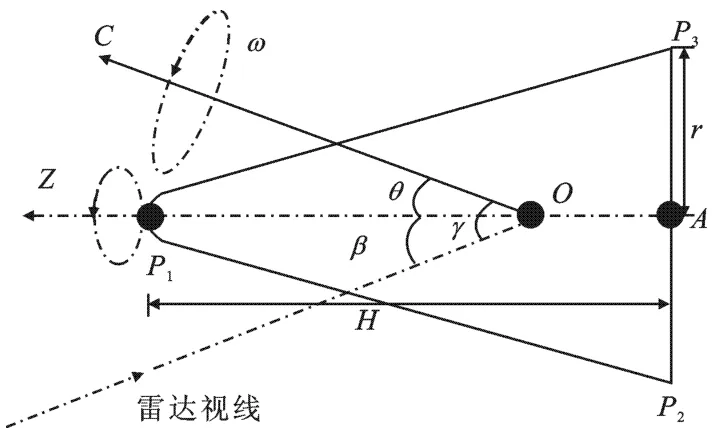
圖1 進動空間錐體目標示意圖

其中,a=cosθcosγ,b=sinθsinγ,ω為目標進動頻率,φ0為初相.當目標位于雷達遠場區時,其表面上起主要作用的有3個散射中心,分別為頂部散射中心P1,底部散射中心P2與P3,其中P2與P3為等效散射中心,由雷達視線和錐體底面共同決定.而對于迎頭飛行的目標來說,P3一般被遮擋,因此主要分析僅P1與P2可見時的情況.

假設目標平動已被補償,進動引發的P1,P2相對雷達距離變化r1（t),r2（t)分別為

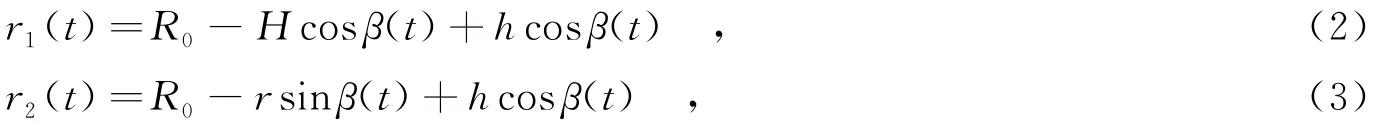
其中R0表示初始距離.由此可推出P1,P2散射點理論微多普勒頻率fm1（t),fm2（t)為

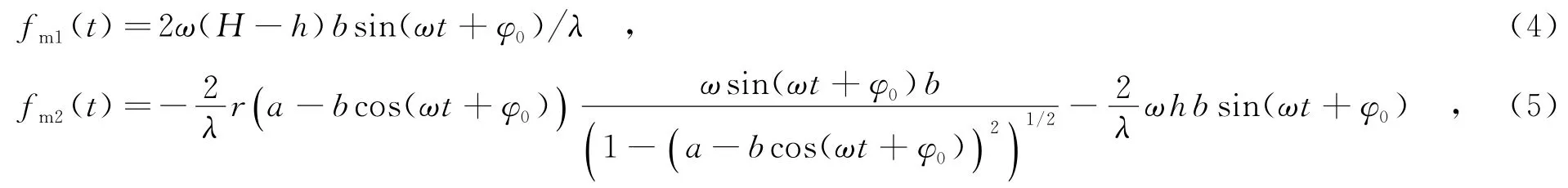
其中λ表示雷達的波長.從理論公式可以看出,頂部散射中心P1微多普勒變化為正弦函數,函數頻率為進動頻率、幅度由進動頻率、目標高度、質心位置、進動角及雷達視線角共同決定.而fm2（t)變化更為復雜,不是一個簡單的正弦函數,包含無窮級的正弦分量.

2 目標尺寸與進動參數估計算法

2.1 底部散射中心回波分析

觀察式（4)與式（5),頂部散射中心微多普勒為正弦曲線,其中可以得到的參數僅為進動頻率,初相意義不大.由于幅度是由多個參數耦合的,因此難以得到更多信息,故筆者重點分析底部散射中心微多普勒幅度.根據式（3),由距離r2（t)推得底部散射中心回波相位φ2（t)為

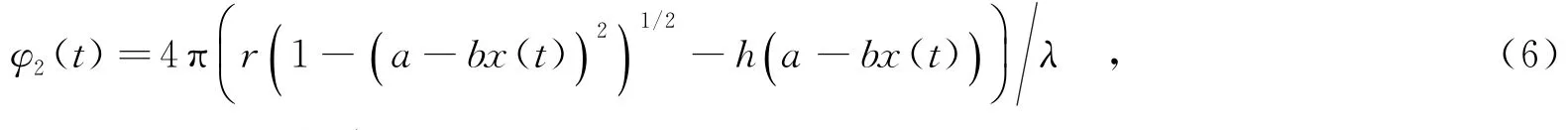
其中,x（t)=cos（ωt+φ0).對式（6)進行泰勒展開,可得

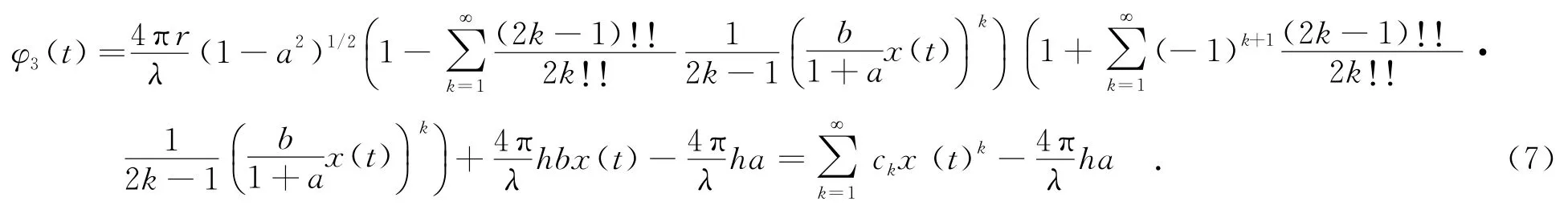
從式（7)可以看出,底部散射中心回波相位是x（t)的無窮級數的線性組合與常數項的結合.根據筆者的推導,其一階系數c1為a,b,r,h的函數,而二階至無窮階系數ck（k＞1)則與h無關,僅為a,b,r的函數.現給出前6階系數:

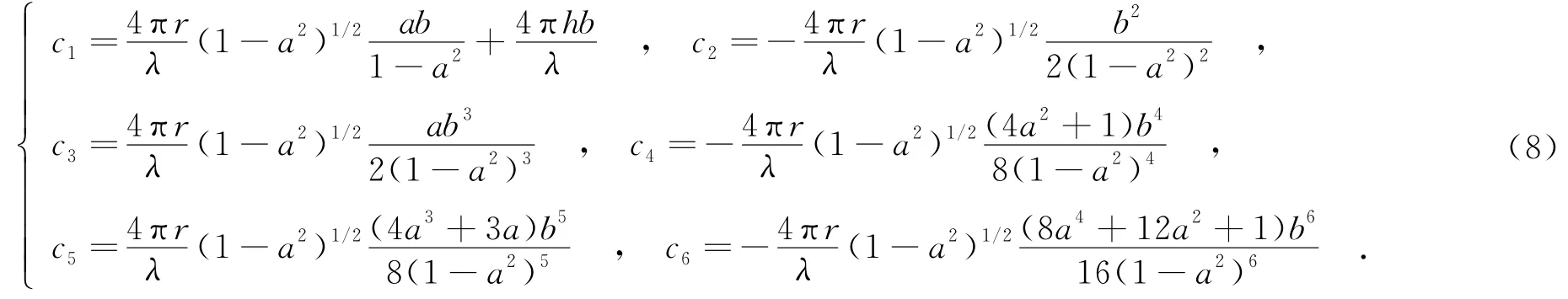
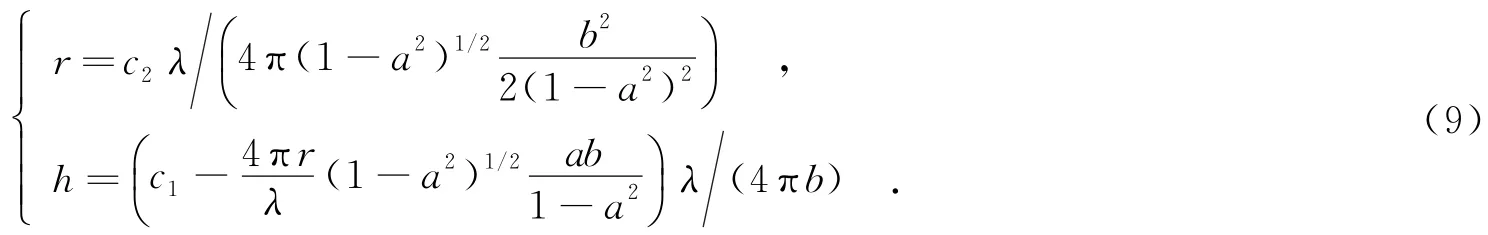
在求解參數a,b,r,h后,利用頂部散射中心微多普勒幅度A=2(ωλ（H-h)b),求解得到目標高度H,而進動角θ與雷達視線角γ可以直接從a,b中得到.

通過上述分析可以看出,在得到級數系數c1～c4后,即可對目標尺寸參數與進動參數進行求解.接下來筆者將根據頂部與底部散射中心微多普勒對系數進行求解.

2.2 系數求解

根據相位與多普勒頻率的關系,對2.1節中推導所得底部散射中心相位式（7)進行求導,可得底部散射中心微多普勒變化fm2（t)為

式（10)即為式（5)的對應展開式.將式（10)離散化,轉化為一個線性方程組的形式,即F=Bc,其中方程組中各元素如下:

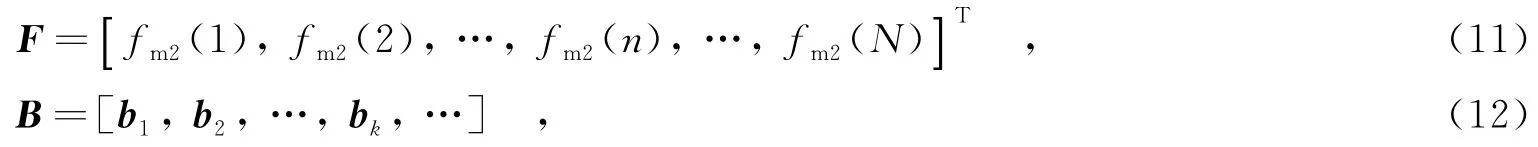
其中,fm2（N)為底部散射中心在時刻N的估計值;bk=[bk（1),…,bk（n),…,bk（N)]T,bk（n)= kx（n)k-1x′（n),x（n)=cos（ωn+φ0),x′（n)=-ωsin（ωn+φ0);c=[c1,c2,…,ck,…]T,為待求系數.可以看出,c=BF,其中B中元素可以通過頂部散射中心微多普勒得到:利用頂部散射中心微多普勒進行正弦擬合,從而得到進動頻率ω,而初相的變化只是相當于微多普勒沿時間平移,并不改變目標參數,因此可設定初相為零,只根據ω構建bk即可,不影響目標參數估計.

至此筆者已經推導出系數c的求解.需要注意的一點是,c有無窮多項,即B的列數可以達到無窮多,而線性方程組只能包含有限的項.經實驗發現,式（7)只要累加到第6階（即k最大為6)時,所得微多普勒與理論微多普勒相比,精度已達到99.996%,滿足計算要求.因此,筆者在構建線性方程組時,只構建B的前6列,即只求得系數c1～c6.

綜上所述,基于微多普勒的進動錐體目標參數估計流程如圖2所示.

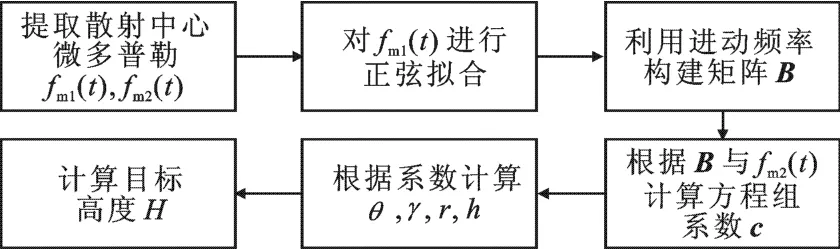
圖2 參數估計流程圖

3 實驗及結果分析

為了對算法性能進行驗證,使用電磁計算數據對目標進行參數估計.計算所用目標模型高度為0.97 m,質心位置為0.15 m,底面半徑為0.25 m,目標進動頻率為2.4 Hz,進動角為7°,雷達視線角設定為36.4°,雷達帶寬為5 MHz,重復頻率為500 Hz,積累時間為1 s,回波HH極化,信噪比設置為25 dB.現有較多從時頻分布中提取目標微多普勒的方法,筆者采用文獻[11]所提算法,利用曲線跟蹤（Curve Tracking,CT)提取微多普勒,提取出的微多普勒如圖3所示,其中頂部與底部散射中心微多普勒可以通過正弦擬合后的殘差來區分,殘差大的為底部分量,小的為頂部分量.

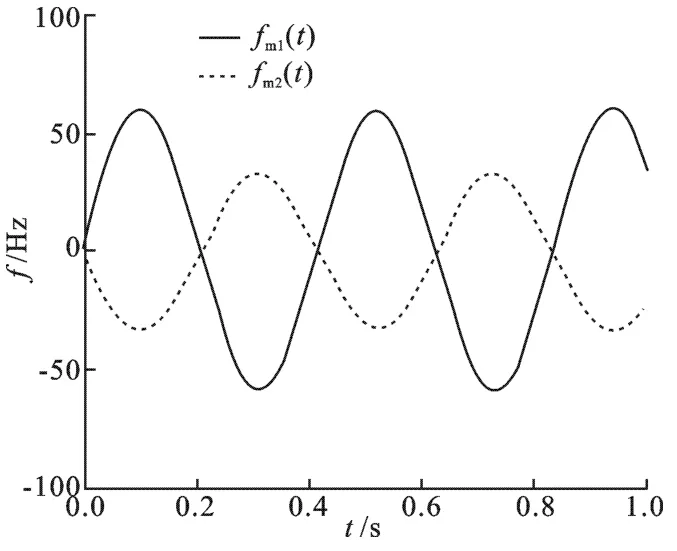
圖3 微多普勒提取結果

對提取出的頂部散射中心微多普勒進行正弦曲線擬合,得到進動頻率ω=2.404 7 Hz,曲線幅度A=58.92 Hz.根據進動頻率構建矩陣B,利用B左除fm2（t),得到系數c1～c6,如表1所示.

根據c2～c4計算a,b,得到a=0.820 7,b=0.064 9.根據a,b與系數c1,c2計算目標底面半徑r與質心位置,最后利用A,h,b,ω計算目標高度H,所得各參數計算值如表2所示.

表1 系數計算結果

表2 參數計算結果

從表2中可以看出,算法有效地對目標的尺寸與進動參數進行了估計,估計精度較高.在當前信噪比條件下,平均估計精度達到了95%以上,其中估計精度的定義為:本算法不涉及耗時較高的運算,例如多維參數搜索,僅利用解線性方程組來求解參數,運算速度較快,在當前參數與平臺（Pentium（R)Dual-Core E6500,主頻2.93GHz,內存2GB)下進行一次參數估計的時間在0.04～0.05 s之間.

為了對本算法的抗噪性能進行評估,筆者在電磁計算數據中注入噪聲,使信噪比從10 d B變化到25 d B,其中信噪比定義為RSN=10 lg（SPNoise),在每種信噪比條件下進行20次實驗,最終所得參數估計精度隨信噪比變化如圖4所示.

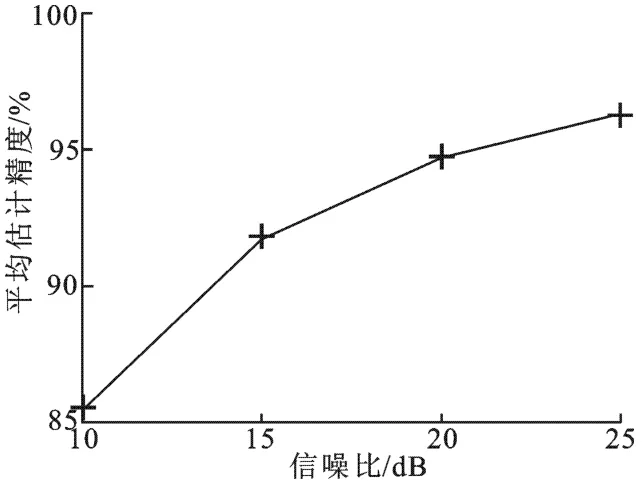
圖4 估計精度隨信噪比變化曲線

從圖4中可以看出,在信噪比大于10 dB時,本算法所得參數估計精度達到85%以上,說明本算法有一定的抗噪性能,而算法的性能也在一定程度上取決于微多普勒提取的精度.需要說明的一點是,仿真結果利用平均信號功率定義信噪比,當目標上不同散射點散射強度相差較大時,要達到相同精度的結果可能需要更高的信噪比.

本算法是利用解線性方程組的形式對參數進行求解的,方程組階數設定為6階,因此在理論上,當獲得6個點的微多普勒估計值時,即可構建矩陣B,進而結合底部散射中心微多普勒進行參數求解,這就使得本算法對積累時間要求較低,并不需要觀測完整的微動周期.為了對本算法在短積累時間內的性能進行評估,估計信噪比為15 dB,變化積累時間從0.1 s到0.5 s,實驗結果如圖5所示.

圖5中的結果顯示,當積累時間為0.1 s時,算法仍然可以對目標參數進行估計,估計精度高于83%;當積累時間達到0.5 s時,估計精度已經基本上與圖4中15 dB的情況相當.這說明了本算法適用于較短積累時間的情況,在實際應用中可以應用于雷達跟蹤多個目標,對單目標積累時間短的場景.這里需要說明的一點是,對于積累時間很短的情況,例如0.1 s時,由于獲得的微多普勒頻率點較少,因此假如獲得的微多普勒集中在兩曲線交點附近時,會對估計結果產生較大的影響.這是因為兩微多普勒曲線相交點為零點,如果利用零點附近的估計值構建線性方程組,會出現類似0=0c的情況,使得方程組奇異,此時較小的微多普勒提取誤差都會帶來很大的參數估計誤差.因此在實際應用中,如果積累時間很短,則應當選取兩散射中心微多普勒差異盡量大的積累時段進行參數估計,以降低這種影響.進一步的實驗也證實,當所提取微多普勒大于完整周期的一半時,這種由方程組奇異帶來的影響就可以被忽略.

圖5 估計精度隨積累時間變化曲線

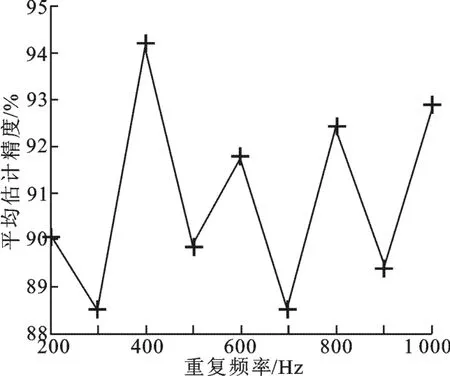
圖6 估計精度隨重復頻率變化曲線

最后對算法估計精度隨雷達重復頻率變化進行分析,估計信噪比設定為15 d B,重復頻率由200 Hz變化到1 k Hz,得到的算法估計精度隨重復頻率變化如圖6所示.

從圖6可以看出,算法估計精度在所設定重復頻率范圍內變化不大,說明算法對于雷達重復頻率變化并不敏感.為了能正確地提取微多普勒頻率變化,要求微多普勒頻率不出現模糊,即fpr＞BmD,其中BmD為微多普勒頻率頻帶寬度.由于仿真實驗中微多普勒頻率帶寬為120 Hz,因此要求雷達重復頻率要高于120 Hz.

4 結束語

筆者提出了一種基于微多普勒頻率的進動錐體目標參數估計算法,利用目標頂部與底部散射中心微多普勒變化構建線性方程組,再利用方程組系數估計得到目標尺寸參數與進動參數.仿真實驗表明:本算法在一定信噪比條件下可以獲得較高的估計精度,且對回波積累時間要求低,運算時間較快.下一步筆者將重點研究低信噪比條件下目標微多普勒提取的問題.

[1] 關永勝,左群聲,劉宏偉,等.空間錐體目標微動特性分析與識別方法[J].西安電子科技大學學報,2011,38(2): 105-111. Guang Yongsheng,Zuo Qunsheng,Liu Hongwei,et al.Micro-motion Characteristic Analysis and Recognition of Coneshaped Targets[J].Journal of Xidian University,2011,38(2):105-111.

[2]Peng L,Sun J P,Wang J,et al.Micro-motion Parameter Estimation of Free Rigid Targets Based on Radar Micro-Doppler[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(10):3776-3786.

[3]Huang J,Ning C,Xiao Z H.Precession and Structural Parameters Estimation of the Cone-Shaped Target Based on the Profile Length[C]//Proceedings of the IEEE International Conference on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber,Physical and Social Computing.Washington:IEEE,2013:1545-1549.

[4]羅迎,張群,李松,等.基于分布式組網雷達的彈道目標三維進動特征提取[J].電子學報,2012,40(6):1079-1085. Luo Ying,Zhang Qun,Li Song,et al.Three-dimensional Precession Feature Extraction of Ballistic Targets in Distributed Radar Networks[J].Acta Electronica Sinica,2012,40(6):1079-1085.

[5] 雷騰,劉進忙,楊少春,等.基于三站一維距離像融合的彈道目標特征提取方法研究[J].宇航學報,2012,33(2): 228-234. Lei Teng,Liu Jinmang,Yang Shaochun,et al.Study on Feature Extraction Method of Ballistic Target Based on Threestation Range Profiles[J].Journal of Astronautics,2012,33(2):228-234.

[6]Feng C Q,Zhang J,Ma Q L.The Estimation of Precession Character Based on Multi-LOS HRRP[J].Applied Mechanics and Materials,2013,2(63):1298-1303.

[7]Gao H W,Xie L G,Wen S L,et al.Micro-Doppler Signature Extraction from Ballistic Target with Micro-motions[J]. IEEE Transactions on Geoscience and Remote Sensing,2010,46(4):1969-1981.

[8]Li P,Wang D C,Wang L.Separation of Micro-Doppler Signals Based on Time Frequency Filter and Viterbi Algorithm [J].Signal,Image and Video Processing,2013,7(3):593-605.

[9]Yao H Y,Li X X,Sun W F,et al.Micro-Doppler Analysis of Nutation Target in Ballistic Midcourse[C]//IET Conference Publications:2013(617CP).Stevenage:IET,2013:0461.

[10]Chen V C,Li Fayin,Ho Shenshyang,et al.Micro-Doppler Effect in Radar:Phenomenon,Model,and Simulation Study [J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):2-21.

[11]李飛,糾博,邵長宇,等.目標微動參數估計的曲線跟蹤算法[J].電波科學學報,2013,28(2):278-284. LI Fei,Jiu Bo,Shao Changyu,et al.Curve Tracking Based Parameter Estimation of Micro-motion[J].Chinese Journal of Radio Science,2013,28(2):278-284.

[12]Liu Y X,Li X,Zhuang Z W.Estimation of Micro-motion Parameters Based on Micro-Doppler[J].IET Signal Processing,2010,4(3):213-217.

（編輯:郭 華)

Parameter estimation method for the cone-shaped target under narrow-band radar observation

HAN Xun,DU Lan,LIU Hongwei
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

The parameter estimation for the space cone-shaped target based on precession is very important for target discrimination.This paper proposes a novel parameter estimation method via the scattering centers’micro-Doppler frequency contained in the narrowband echo.After the establishment of the target’s precession model,the theoretical variation of top and bottom scattering centers’micro-Doppler frequency are derived,and then the micro-Doppler frequency of the bottom scattering center is expanded,and the relationship between the expansion coefficients and the target’s size and precession parameter is analyzed. Finally,a linear system of equations is established to solve the expansion coefficients with the top and bottom scattering centers’micro-Doppler frequencies,and then the target’s size and precession parameters are calculated based on the coefficients.Experiments based on electromagnetic computation data indicate that the proposed method is valid and accurate.

target recognition;cone-shaped target;micro-Doppler frequency;parameter estimation; feature extraction

TN957.52

A

1001-2400（2015)06-0043-06

10.3969/j.issn.1001-2400.2015.06.008

2014-06-16

時間:2015-03-13

國家自然科學基金資助項目（61271024,61201296,61322103);全國優秀博士學位論文作者專項資金資助項目（FANEDD-201156)

韓 勛（1990-),男,西安電子科技大學博士研究生,E-mail:andyhanxun@126.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150313.1719.008.html