不同移動模型下無線多播性能預測模型

譚國平，楊 陽，霍孝義，居美艷

（河海大學 計算機與信息學院 通信與信息系統研究所，江蘇 南京211100）

0 引 言

網絡編碼的概念，使得網絡能夠達到最大流最小割定理所確定的最大理論容量，因而被廣泛研究用于提高網絡吞吐率、安全性、能量利用率［1－3］。文獻 ［4］將網絡編碼技術添加到多播路由協議中，提出了基于部分網絡編碼［5］的實時多播協議PNCRM。本文運用多元回歸分析對PNCRM 協議建模分析。

多元回歸分析在預測方面的應用已經非常廣泛。文獻［6］提出基于穩健回歸分析的實時多播協議性能預測方法，通過給定網絡場景參數能夠較好地預測協議性能，但其只選擇了單個移動模型進行分析，且在網絡仿真場景中各節點移動速度是隨機的，無法準確描述節點移動速度對路由總開銷的影響。本文針對文獻 ［6］的不足選取隨機路點、高斯馬爾科夫和參考點組3種典型的移動模型對穩健回歸分析的實時多播協議性能預測模型進行對比研究。通過對網絡仿真場景中所有節點移動速度設為同一隨機值，可以準確反映節點移動速度對路由總開銷的影響，驗證了該模型具有很好的預測性能。

1 移動模型

為了研究穩健回歸分析的實時多播協議性能預測模型的預測效果，除了NS2中已有的隨機路點移動模型，我們將高斯馬爾科夫以及參考點組移動模型加入NS2中，對比預測模型在3種不同移動模型下的性能表現。

1.1 隨機路點移動模型

隨機路點移動模型［7］（rand waypoint mobility model，RWP）簡單，易于實現，且應用廣泛。在該模型中，節點首先在隨機位置上選擇一個隨機目的地，以速度v朝著目的地移動，到達后停留一段時間Tpause，再以本次的目的地作為下次移動的起點，隨機選擇另一目的地，然后繼續重復上述過程。其中，v∈［vmin，vmax］，服從均勻分布，vmin是節點最小移動速度，vmax是節點最大移動速度。Tpause∈［Tmin，Tmax］，服從均勻分布，Tmin、Tmax分別為節點最小暫停時間和最大暫停時間。

1.2 高斯馬爾科夫移動模型

高斯馬爾科夫移動模型［8］（Gauss－Markov mobility model，GM）中，節點在任意一個時刻的速度與先前一個時刻速度相關，因此節點的運動速度是平滑的，避免了速度或方向的突變行為。速度和方向計算公式如下

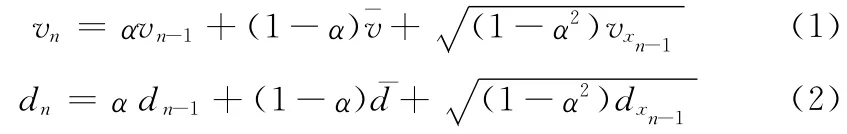
其中，vn和dn為節點在第n個時間間隔的速度和方向；α（α∈［0，1］）用來調節隨機性；和表示當n→∞時速度和方向的平均值；vxn－1和dxn－1服從Gaussian分布。

在第n個時間間隔，節點的位置公式如下

其中，（xn，yn），（xn－1，yn－1）是節點在第n，n－1個時間間隔的坐標；vn－1，dn－1是節點在第n－1個時間間隔的速度和方向。

1.3 參考點組移動模型

參考點組移動模型［9］（reference point group mobility model，RPGM）是一種群組移動模型，在該模型中，每個組有一個稱為參考點的邏輯中心，組邏輯中心的移動決定整組節點的移動。組內節點的移動是將組邏輯中心作為參考點，在其周圍自由移動。假設同一組內的節點P、Q 在t1時刻的速度矢量公式為

上面描述的3種移動模型中，隨機路點移動模型和高斯馬爾科夫移動模型下各節點之間的移動是相互獨立的，而參考點組移動模型節點以群組的模式移動，組內節點的移動并不是完全獨立的，邏輯中心的移動決定本組節點的移動屬性。通過加入3 種典型的移動模型，更好地反映PNCRM 協議的性能表現。

2 仿真數據及模型應用

2.1 PNCRM 仿真參數

為了獲得PNCRM 性能預測模型的原始數據，通過設置不同的編碼塊長度、節點移動速度和接收節點個數取值來構造不同的網絡場景并在NS2中進行仿真，然后對產生的追蹤文件進行處理。

仿真場景見表1。

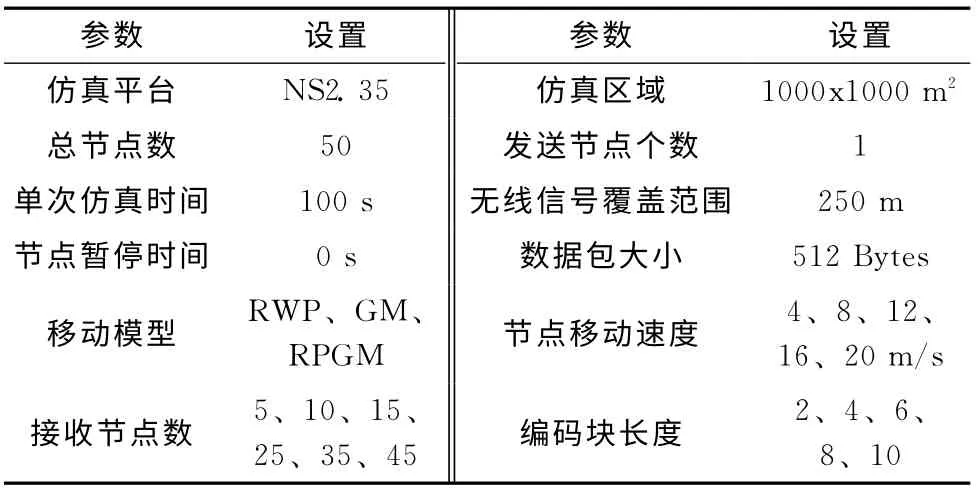
表1 PNCRM 仿真參數設置

2.2 預測模型構建

根據多元回歸分析理論［10，11］，構建PNCRM 協議性能的預測模型，本文采用多項式函數作為各自變量與性能指標的關系類型

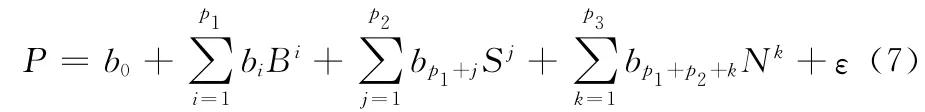
式中：P——協議性能；B——編碼塊長度；S——節點移動速度，每組仿真場景中所有節點的速度為同一隨機值；N——節點個數；b0，b1，…，bp1＋p2＋p3是需要求解的回歸系數，p1，p2，p3——各自變量的最高階次，ε——隨機誤差項。

仿真實驗中選取n組原始數據，n越大求得的回歸方程系數越精確。回歸方程的矩陣表示如下

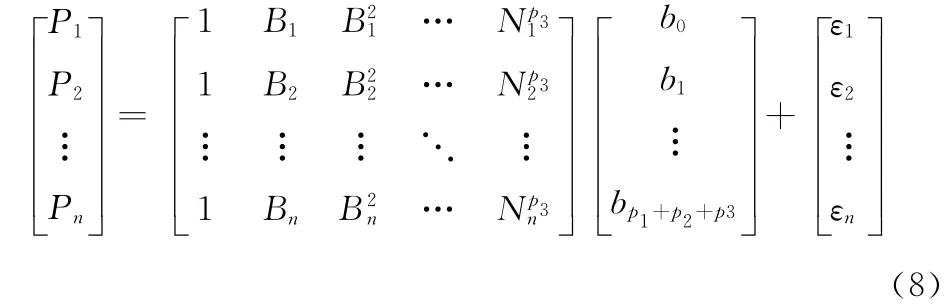
實驗過程中，為了全面評估PNCRM 協議的性能，選取了3個指標進行性能評估，分別是：

分組投遞率 （packet delivery ratio）：它是接收節點收到的分組數與發送節點發送的分組數比值。分組投遞率反映了路由協議的可靠性和正確性，特別是是在拓撲結構高度動態的移動自組網中，路由協議的可靠性至關重要，因此具有較高的分組投遞率是設計移動自組網路由協議的一大準則。

總開銷 （total overhead）：發送的控制分組數、數據分組數之和與接收到的數據分組數之比。它反映了路由協議的效率問題，由于移動自組網中無線帶寬資源有限，因此路由協議的總開銷越小越好。

端到端延時 （delay）：指分組從發送端到接收端所經歷的時間。端到端延時直接影響通信服務質量和用戶的滿意度，對實時性業務影響更是如此。

本文選取總開銷這一性能指標進行建模分析。運用極大似然估計的迭代加權最小二乘法對矩陣進行求解。

2.3 模型參數確定

因為多項式函數 （4）中各自變量的最高階次未知，求解之前需要先確定P1，P2，P3的值。下面給出確定P3值的求解過程，P1，P2同理可得。

本文原始數據值個數n取150，NS2中仿真得到接收節點個數 （N）為5、10、15、25、35、45時與之對應的協議總開銷 （TO） 平均值分別為4.883296、3.277822、2.399537、1.537478、1.125066、0.877239。將得到的數據導入Matlab的Cftool工具箱并選擇多項式逼近，使用最小二乘擬合算法確定函數關系式。通過殘差平方和、調整的判定系數和均方根誤差3個指標作為判定擬合效果的標準。擬合效果如圖1所示，得到TO 函數關系式

由式 （9）可知P3值為3，同理P1、P2值分別為3、3。所以TO 預測模型為

圖1 協議總開銷與接收節點個數的擬合效果

2.4 模型求解及檢驗

最小二乘估計是常用的求解回歸系數的方法，在一切無偏估計類中，具有最小的方差。但是，當實際觀測值中出現異常值時，隨機誤差項將不再服從正態分布，而是重尾分布，此時用最小二乘法求解回歸系數是不準確的。采用極大似然估計 （M－估計）［12］的穩健回歸分析能夠有效地解決最小二乘法的不足，穩健回歸在識別異常值方面具有顯著的優越性。

在極大似然估計中，通過最小化一個關于殘差的目標函數ρ對回歸系數β進行求解，即

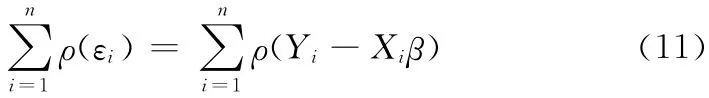
通過比較發現最小二乘法的目標函數就是

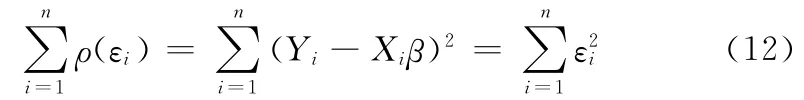
令ψ＝ρ′為目標函數關于回歸系數β的導數，在穩健回歸中稱之為影響函數。為了求目標函數的最小值，令目標函數的導數為0 即可求得，則對上式求關于回歸系數β的導數得

由以上分析可知權重由殘差求得，殘差由回歸系數求得，而回歸系數的求解又與權重有關，所以式 （14）的求解需要用迭代法，此過程稱為迭代加權最小二乘法 （iteratively reweighted least－squares，IRLS）。

目標函數為Bisquare函數，其形式如下

求導得其權重函數為

其中，k為調和常數，為了能夠提供95%的有效性且排除異常值的干擾，常取k ＝4.685σ，σ為殘差的標準差，在實際應用中需用估計量代替。

根據式 （10）構建的預測模型，借助Matlab編程使用極大似然估計的迭代加權最小二乘法求解，得到表2。

采用多元回歸模型的兩種檢驗方法：①方程顯著性檢驗，即F檢驗值反映回歸模型效果的顯著性。由F 分布表得F10，139（0.01）＝2.5365，表2 中F 檢驗值428.09382.5365，所以認為此回歸模型高度顯著。②變量顯著性檢驗，即t檢驗值反映某個自變量對預測變量影響的顯著性。由t分布表得t0.025（140）＝1.9771，所以表2中由t檢驗值可以刪除B2、B3、S、S2和S3。

表2 TO 預測模型求解值

對式 （10）進行刪除項處理，得到新的預測模型，運用Matlab編程求解，得到表3。

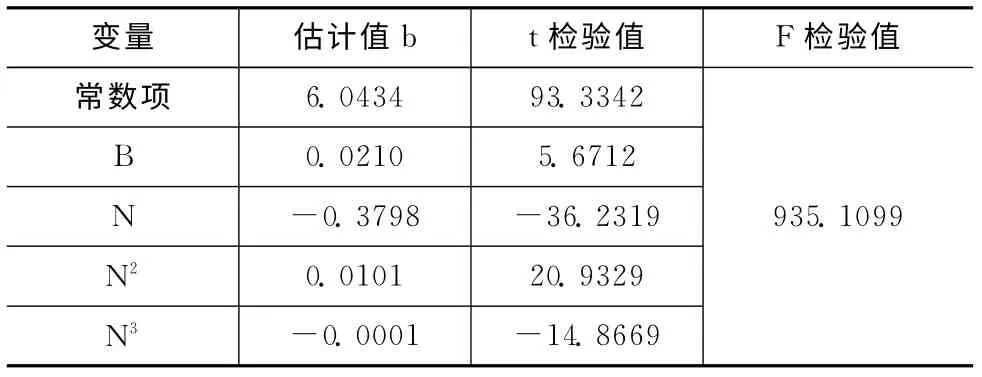
表3 重構后TO 預測模型求解值

由F分布表得F4，145（0.01）＝3.4512，表3中F檢驗值935.1099＞＞3.4512，認為此回歸模型高度顯著。由t分布表得t0.025（145）＝1.9765，所以表3中t檢驗值均滿足顯著性要求。因此，得到

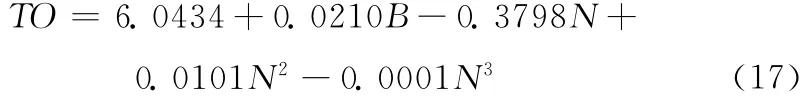
同理，求得隨機路點移動模型下預測模型為

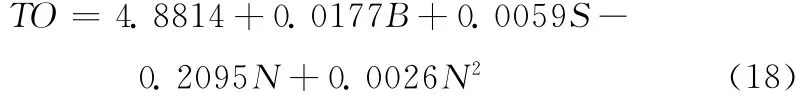
參考點組移動模型下預測模型為

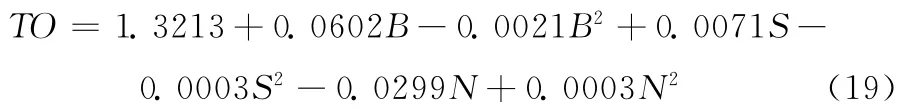
3 預測模型分析

運用多元回歸分析構建PNCRM 性能預測模型的最終目的是預測PNCRM 在不同場景參數下的性能表現。為了檢驗所構建PNCRM 性能預測模型的預測效果，本文通過修改仿真參數選取不同于構建性能預測模型時自變量的取值來獲得總開銷 （TO）的觀測值，對比其與通過所構建性能預測模型得到的預測值的差值，并計算其平均相對誤差來衡量其預測效果，各自變量的取值及其它場景參數設置見表4。

表4 PNCRM預測模型檢驗仿真參數設置

通過改變節點移動速度和接收節點個數的取值組合產生不同的仿真場景，同樣地，每個場景仿真多次取其平均值作為此場景下性能的最終值，其它參數與表1 的設置相同。

本文利用RWP、GM、RPGM 這3種移動模型，檢驗所構建的PNCRM 性能預測模型的預測效果。圖2、圖3、圖4分別描述了3種移動模型的應用效果。

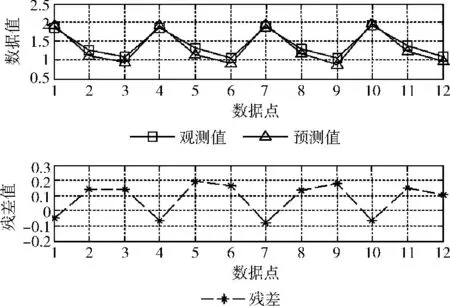
圖2 隨機路點移動模型的TO 預測模型應用

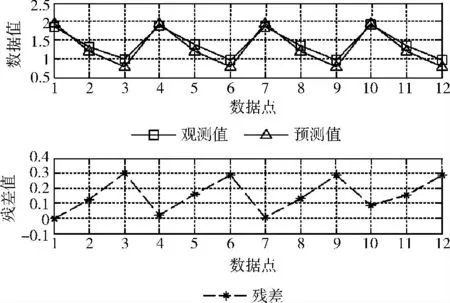
圖3 高斯馬爾科夫移動模型的TO 預測模型應用

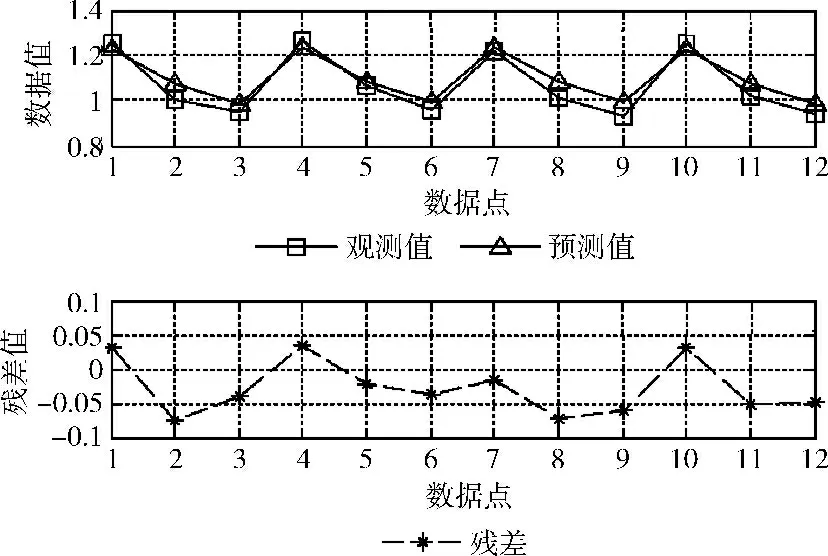
圖4 參考點組移動模型的TO 預測模型應用

圖2、圖3、圖4 中各有3 條曲線，數據點標記符中，方塊是觀測值曲線，三角是預測值曲線，星號是殘差值曲線。

4 結 論

由3組預測模型應用圖可以發現，3種移動模型下TO預測模型的觀測值曲線與預測值曲線基本吻合，計算得其平均相對誤差分別為8.56%、9.27%、4.03%。比較可知，參考點組移動模型的TO 預測模型的誤差變化范圍明顯小于其它兩種移動模型，這是因為參考點組移動模型下的總開銷比其它兩種小得多，使得取值范圍較小，進而誤差值也相對較小。圖中同樣可以發現，高斯馬爾科夫移動模型下TO 預測模型的殘差值大部分為正值，而不是在0 值附近上下波動，且具有最大的平均相對誤差，這是在以后的研究中需要改進的地方。同時，我們可以發現TO 預測模型的平均相對誤差比較大，這是主要因為構建TO 預測模型所使用原始數據中的TO 值在1 至6 之間，變化范圍較大。總體說來，所構建的預測模型能較準確地預測PNCRM 的TO 性能。

5 結束語

本文選取隨機路點移動模型、高斯馬爾科夫移動模型、參考點組移動模型分析PNCRM 性能預測模型的預測效果。預測模型在3種移動模型下所做預測的值與觀測值的平均相對誤差分別僅為8.56%、9.27%、4.03%，具有很好的預測效果。因預測模型中僅研究了編碼塊長度、節點移動速度、接收節點個數對預測性能影響，忽略了如編碼包緩沖區長度，接收節點密度等其它因素的影響。未來的工作中一方面需要考慮這些因素對PNCRM 性能的影響，另一方面應該進一步探索對預測模型的簡化處理，構建更加精確的預測模型。

［1］Zhang Z.Theory and applications of network error correction coding ［C］／／Proceedings of the IEEE，2011：406－420.

［2］Wang S，Vasilakos A，Jiang H，et al.Energy efficient broadcasting using network coding aware protocol in wireless ad hoc network ［C］／／Proc IEEE ICC，2011.

［3］Paramanathan A，Heide J，Pahlavani P，et al.Energy and data throughput for asymmetric intersession network coding［C］／／IEEE 17th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks，2012：358－363.

［4］TAN Guoping，PENG Xinhua，NI Xinyang，et al.Research on partial network coding based real－time multicast protocols in mobile Ad－Hoc networks ［J］.Microelectronics＆Computer，2012，29 （9）：39－41 （in Chinese）.［譚國平，彭新華，倪新洋，等.基于部分網絡編碼的移動自組網實時多播協議研究［J］.微電子學與計算機，2012，29 （9）：39－41.］

［5］Guo Bin，Chang Peiqiang，Lin Yu，et al.A practical network coding scheme over GF （2q）for multi－user cooperative communication ［C］／／IEEE Globecom，2011：1－5.

［6］TAN Guoping，HUO Xiaoyi，TAN Linfeng，et al.A method to predict the performance of wireless real－time multicast protocol based on robust regression analysis ［J］.Journal of Hohai University （Natural Sciences），2013，41 （6）：554－559 （in Chinese）.［譚國平，霍孝義，譚林風，等.基于穩健回歸分析的實時多播協議性能預測方法 ［J］.河海大學學報 （自然科學版），2013，41 （6）：554－559.］

［7］Simaremare H，Syarif A，Abouaissa A，et al.Energy Consumption analysis of modified AODV routing protocol under random waypoint and reference point group mobility models［C］／／International Conference on Advanced Computer Science and Information Systems，2012：28－29.

［8］Rohrer JP，Cetinkaya EK，Narra H，et al.AeroRP performance in highly－dynamic airborne networks using 3D Gauss－Markov mobility model［C］／／Proceedings of Military Communications Conference.IEEE，2011：834－841.

［9］Amjad K.Performance analysis of DSR protocol under the influence of RPGM model in mobile AD－HOC networks ［C］／／31st International Conference on Distributed Computing Systems Workshops.IEEE，2011：100－104.

［10］Mohammad H Mokhtari，Ibrahim Busu，Hossein Mokhtari，et al.Neural network and multiple linear regression for estimating surface albedo from ASTER visible and near－infrared spectral bands［J］.Earth Interact，2013，17 （3）：1－20.

［11］Seal Victor，Raha Arnab，Maity Shovan，et al.A real time multivariate robust regression based flood prediction model using polynomial approximation for wireless sensor network based flood forecasting systems［C］／／Advances in Computer Science and Information Technology，2012：432－441.

［12］Yao Lili，Song Xiangdong.Variable bandwidth M－estimators of the partial linear regression models ［C］／／International Conference on Multimedia Technology，2011：2793－2796.