不確定性數(shù)據(jù)的超球支持向量機(jī)分類(lèi)方法

李文進(jìn)，熊小峰，毛伊敏

（1.江西理工大學(xué) 理學(xué)院，江西 贛州341000；2.江西理工大學(xué) 應(yīng)用科學(xué)學(xué)院，江西 贛州341000）

0 引 言

在數(shù)據(jù)分類(lèi)領(lǐng)域，現(xiàn)有方法的研究往往是針對(duì)確定性數(shù)據(jù)提出，不能直接用于處理不確定性數(shù)據(jù)，且數(shù)據(jù)的不確定性對(duì)分類(lèi)結(jié)果的可靠性具有不可忽視的影響，因此面向不確定性數(shù)據(jù)分類(lèi)方法的研究具有重要的意義［1－3］。

針對(duì)屬性級(jí)不確定性數(shù)據(jù)［2，3］的分類(lèi)問(wèn)題，國(guó)內(nèi)外的研究方興未艾，并取得一定具有代表性的研究成果，主要有基于決策樹(shù)的不確定性數(shù)據(jù)分類(lèi)方法［4］、基于樸素貝葉斯的不確定性數(shù)據(jù)的分類(lèi)方法［5，6］、基于規(guī)則的不確定性數(shù)據(jù)分類(lèi)方法［7］等。現(xiàn)有基于支持向量機(jī) （SVM）分類(lèi)方法的研究主要基于隨機(jī)理論，視樣本為滿(mǎn)足某種已知分布的隨機(jī)變量［8，9］。文獻(xiàn) ［10］提出USVC、AUSVC 及MPSVC3種方法，這3種方法均采用多維高斯分布描述數(shù)據(jù)的不確定性。其中，USVC算法建立了SVC分類(lèi)器的不確定性機(jī)會(huì)約束規(guī)劃問(wèn)題，并將問(wèn)題轉(zhuǎn)化為二階錐規(guī)劃求解問(wèn)題。AUSVC 方法和MPSVC 方法均基于USVC 方法求解基本解，并通過(guò)特定手段迭代調(diào)整各訓(xùn)練樣本對(duì)應(yīng)的機(jī)會(huì)約束的置信參數(shù)，從而減小噪聲樣本對(duì)分類(lèi)器的影響。

基于隨機(jī)理論的方法需要大量的樣本信息來(lái)構(gòu)建概率分布函數(shù)。然而，實(shí)際工程應(yīng)用中滿(mǎn)足隨機(jī)性假設(shè)要求的樣本數(shù)據(jù)通常是缺乏的，但不確定性信息的界限卻容易獲得［8］，這類(lèi)不確定性被稱(chēng)為非概率有界不確定性［3，8，9］，所對(duì)應(yīng)的數(shù)據(jù)稱(chēng)為區(qū)間不確定性數(shù)據(jù)。標(biāo)準(zhǔn)結(jié)構(gòu)支持向量機(jī)是針對(duì)二分類(lèi)提出的，在處理多分類(lèi)時(shí)具有計(jì)算復(fù)雜度較高的局限［11］。超球支持向量機(jī)是一種具有較低計(jì)算復(fù)雜度的球結(jié)構(gòu)支持向量機(jī)分類(lèi)方法［12－14］。

因此，針對(duì)區(qū)間不確定性數(shù)據(jù)分類(lèi)問(wèn)題，本文基于球結(jié)構(gòu)支持向量機(jī)，提出了區(qū)間不確定性超球支持向量機(jī)（interval uncertainty hyper－sphere support vector machine，IUHSVM）。仿真結(jié)果表明，該算法具有一定的抗不確定性噪聲干擾的能力，且具有較優(yōu)的分類(lèi)精度和魯棒性。

1 不確定數(shù)據(jù)模型

1.1 區(qū)間數(shù)的基本概念

非概率有界不確定性在科學(xué)研究和工程實(shí)際中有廣泛的應(yīng)用背景，往往采用區(qū)間數(shù)描述。區(qū)間數(shù)通常定義為一對(duì)有序的實(shí)數(shù)［3，8，9］

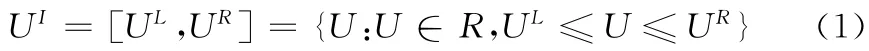
式 （1）中UR表示區(qū)間上界，UL表示區(qū)間下界，若有UR＝UL，則該區(qū)間退化為實(shí)數(shù)。記I（R）一維區(qū)間數(shù)集合，UI也可以定義為如下形式

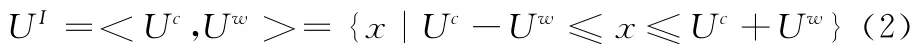
式 （2）中Uc和Uw分別表示區(qū)間UI的中點(diǎn)和半徑

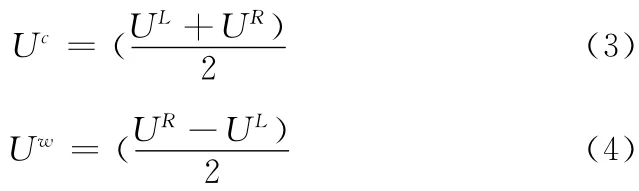
1.2 超橢球凸集模型

非概率集合理論模型是研究有界不確定性?xún)?yōu)化的數(shù)學(xué)方法和理論，主要分為兩類(lèi)［8，9］：一類(lèi)基于凸模型優(yōu)化理論，另一類(lèi)基于區(qū)間數(shù)優(yōu)化理論 （凸模型的一種特例）。本文基于凸模型理論，采用超橢球凸集模型［8，9］描述區(qū)間向量的不確定性信息。記m 維區(qū)間向量U ＝［u1，u2，…，um］∈I（Rm），則區(qū)間向量的不確定性信息可采用一個(gè)多維的超橢球凸集EU來(lái)量化

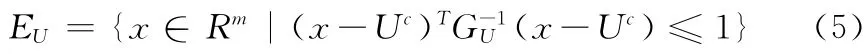
式 （5）中，GU表示超橢球凸集模型的特征矩陣，是一個(gè)m×m 階的正定矩陣

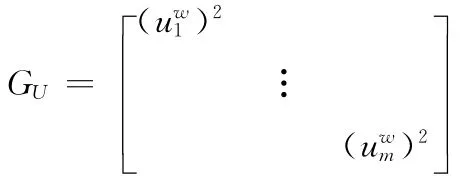
2 區(qū)間不確定性超球支持向量機(jī)

2.1 IUHSVM 數(shù)學(xué)模型

針對(duì)區(qū)間不確定數(shù)據(jù)分類(lèi)問(wèn)題，每個(gè)樣本表現(xiàn)為區(qū)間向量形式，簡(jiǎn)稱(chēng)區(qū)間樣本。本文結(jié)合超橢球凸集模型，提出區(qū)間不確定性超球支持向量機(jī)分類(lèi)方法 （IUHSVM）。與傳統(tǒng)的超球支持向量機(jī)相似，IUHSVM 的分類(lèi)策略如下：將每一類(lèi)區(qū)間樣本的超橢球凸集用最小包圍球界定 （超球體），并通過(guò)各超球判斷某個(gè)樣本是否屬于該類(lèi)。

支持向量機(jī)通過(guò)引入核函數(shù)，將輸入變量xi從樣本空間映射到高維特征空間中構(gòu)造最優(yōu)超平面，解決了非線性數(shù)據(jù)的分類(lèi)問(wèn)題。

假設(shè)從樣本空間到高維特征空間H 的映射為

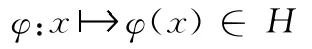
則核函數(shù)與內(nèi)積運(yùn)算相應(yīng)表示為

樣本空間是特征空間的一個(gè)特例，不失一般性，本文直接給出區(qū)間不確定性數(shù)據(jù)在特征空間中的分類(lèi)方法：

對(duì)于m 維屬性區(qū)間不確定性樣本集：Xi，i＝1，2，…l，Xi∈I（Rm）。IUHSVM 模型的最優(yōu)超平面可以通過(guò)求解下面的不確定性約束規(guī)劃問(wèn)題得到

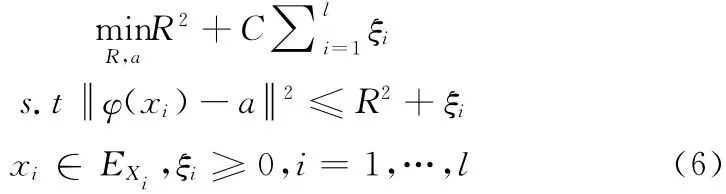
式中：a——球心；R——球半徑；ξ——松弛因子；C——懲罰因子，用于控制模型訓(xùn)練精度和泛化性能的平衡；xi——區(qū)間樣本范圍內(nèi)的不確定向量；EXi——區(qū)間樣本的超橢球凸集，表示樣本的不確定域。

問(wèn)題 （6）是不確定性凸模型優(yōu)化問(wèn)題，通常采用Elishakoff提出的基于 “最差情況”處理的不確定優(yōu)化方法［8］求解，則問(wèn)題 （6）可轉(zhuǎn)化為確定性約束規(guī)劃問(wèn)題

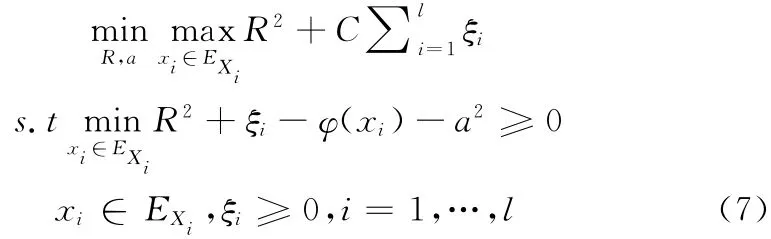
問(wèn)題 （7）是一個(gè)兩層嵌套的凸模型優(yōu)化問(wèn)題［8］，外層優(yōu)化用于設(shè)計(jì)向量尋優(yōu)，內(nèi)層優(yōu)化用于求取不確定性目標(biāo)函數(shù)和約束在不確定域的最不利響應(yīng)。

2.2 IUHSVM 模型的求解方案設(shè)計(jì)

目前，針對(duì)嵌套凸模型優(yōu)化求解方法在理論和算法研究上還不完善，仍未發(fā)展出適應(yīng)性較強(qiáng)的高效率通用求解算法。如文獻(xiàn) ［10］將凸集機(jī)會(huì)約束規(guī)劃轉(zhuǎn)化為二階錐規(guī)劃，導(dǎo)致大量的冗余變量，計(jì)算效率極低。為了降低嵌套凸模型優(yōu)化求解算法的計(jì)算復(fù)雜度，通常根據(jù)問(wèn)題特殊結(jié)構(gòu)設(shè)計(jì)求解方法，如通過(guò)分解技術(shù)［8，15，16］將兩層嵌套優(yōu)化問(wèn)題轉(zhuǎn)轉(zhuǎn)化為上下兩層子優(yōu)化交替迭代尋優(yōu)求解的問(wèn)題，則問(wèn)題 （7）可轉(zhuǎn)為形式如下：

上層優(yōu)化問(wèn)題

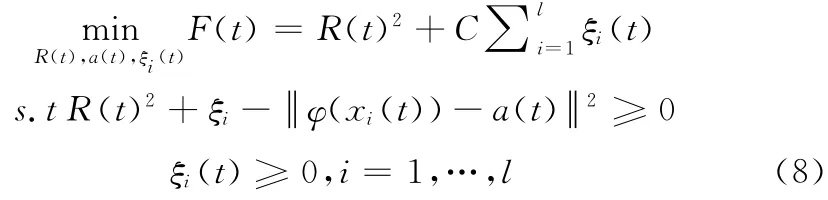
下層優(yōu)化問(wèn)題

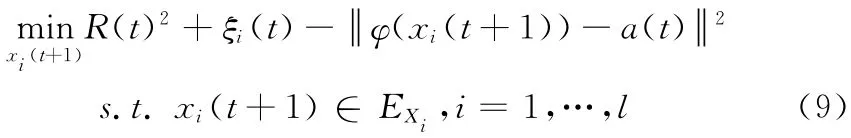
問(wèn)題 （8）和問(wèn)題 （9）中，t表示迭代的次數(shù)。其中，問(wèn)題 （8）是常規(guī)形式的球結(jié)構(gòu)支持向量機(jī)，可以使用其對(duì)偶問(wèn)題求解

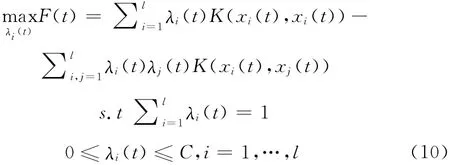
此時(shí)，求解問(wèn)題 （7）等價(jià)于通過(guò)對(duì)子優(yōu)化問(wèn)題 （9）和問(wèn)題 （10）的交替迭代求解，直至收斂得到的最優(yōu)解。非線性凸集規(guī)劃直接求解計(jì)算復(fù)雜度大，通常通過(guò)泰勒展開(kāi)法，根據(jù)凸集的特殊結(jié)構(gòu)，求解其線性近似規(guī)劃問(wèn)題［15，16］，從而得到近似最優(yōu)解。問(wèn)題 （9）是滿(mǎn)足超橢球凸結(jié)構(gòu)的非線性凸集規(guī)劃，因此可以直接通過(guò)泰勒展開(kāi)的線性近似問(wèn)題推導(dǎo)得到其不確定量xi（t＋1）的近似最優(yōu)解。下面給出IUHSVM 算法模型中下層優(yōu)化問(wèn)題中的不確定量xi（t＋1）的求解方法：

核函數(shù)K（x，y）＝φ（x）Tφ（y）包含兩個(gè)參數(shù)x和y，當(dāng)固定其中一個(gè)參數(shù)時(shí)，核函數(shù)可以被視為以另一個(gè)參數(shù)為自變量的函數(shù)。例如：固定y，則K（x，y）可以被視為以x為自變量的函數(shù)。此時(shí)，核函數(shù)關(guān)于x 的一階泰勒展開(kāi)式可表示為

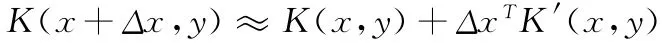
其中，K′（x，y）表示核函數(shù)在y處關(guān)于x 的偏導(dǎo)數(shù)。IUHSVM 算法中下層最優(yōu)問(wèn)題 （9）的求解方法如下：

定理1 在IUHSVM 算法中，下層優(yōu)化問(wèn)題 （9）的最優(yōu)解xi（t＋1）是

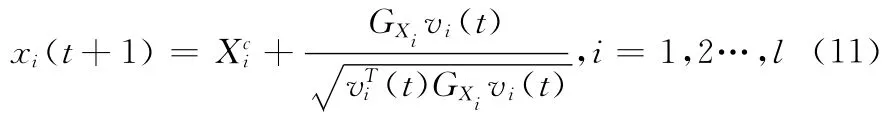
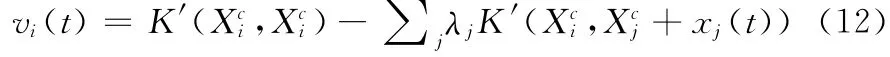
證明：在問(wèn)題 （9）中，R（t），a（t）為已知，則問(wèn)題 （9）等價(jià)于下面問(wèn)題

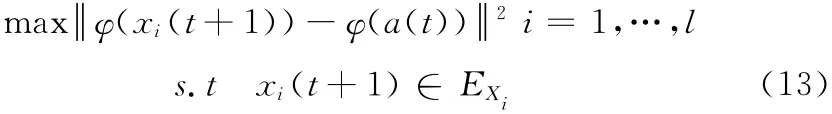
不確定量可用區(qū)間樣本均值和偏移量表示

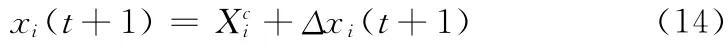
將式 （14）帶入問(wèn)題 （13）的目標(biāo)函數(shù)，并用泰勒公式展開(kāi)得

由題設(shè)條件可知， φ（Xci）－φ（a（t））2為常數(shù)，將式（12）帶入式 （15），并化簡(jiǎn)，問(wèn)題 （13）等價(jià)于下面的問(wèn)題

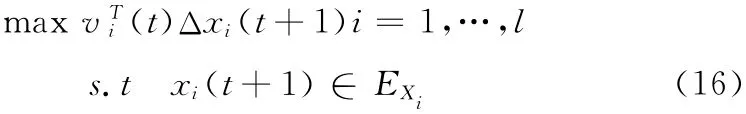
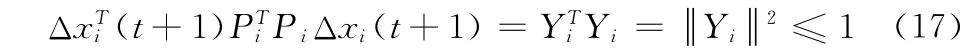
由式 （17） 和 Cauchy－Schwarz 不等式可知， 當(dāng)取得最大值時(shí)，向量Yi與同方向且，令

其中，c為正常量系數(shù)，其值越大，問(wèn)題 （16）的目標(biāo)值越大，將式 （18）帶入式 （17）中，得

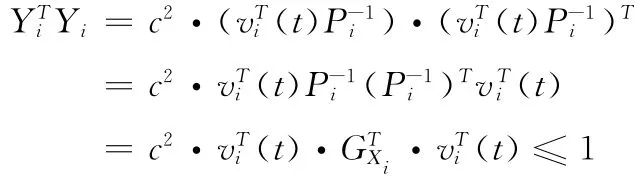
因此可知，當(dāng)c取最大值時(shí)，有

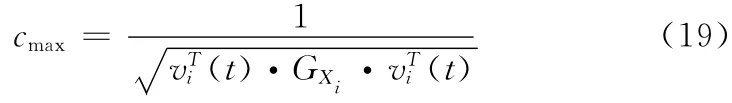
所以，問(wèn)題 （16）的最優(yōu)解為

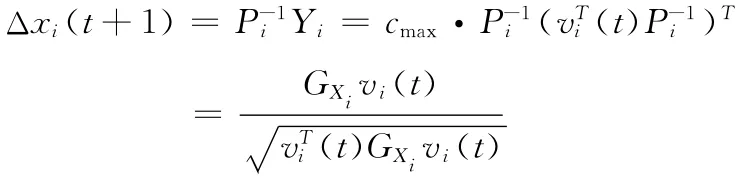
因此，下層優(yōu)化問(wèn)題 （9）的最優(yōu)解

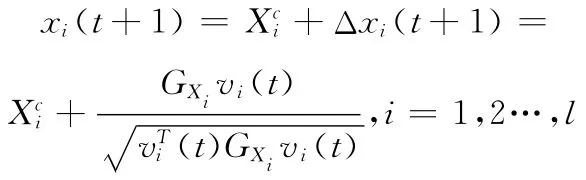
定理1得證。

IUHSVM 求解算法的基本流程如下所示：

步驟1 初始化

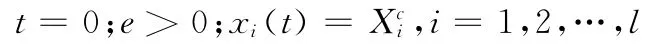
步驟2 計(jì)算上層優(yōu)化問(wèn)題：帶入｛xi（t）｜i＝1，2，…，l｝，求解問(wèn)題 （10）（當(dāng)t＞0時(shí)，設(shè)置搜索初值為λi（t－1），i＝1，2，…，l），得到λi（t），i＝1，2，…，l，并計(jì)算：R（t），a（t），ξi（t）；

步驟3 算法收斂檢驗(yàn)：若‖F(xiàn)（t）‖≤e：算法結(jié)束，輸出R（t），a（t），xi（t）；否則轉(zhuǎn)至步驟4；

步驟4 計(jì)算下層優(yōu)化問(wèn)題，迭代更新：將a（t）帶入式 （11）、式 （12），計(jì)算下層優(yōu)化的近似最優(yōu)解

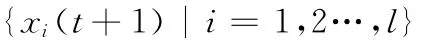
令t＝t＋1，轉(zhuǎn)至步驟2，直至滿(mǎn)足收斂條件。

預(yù)測(cè)分類(lèi)策略為：分別計(jì)算未知類(lèi)別樣本到各超球中心距離與該超球半徑的比值，并將樣本劃分到比值最小的超球所對(duì)應(yīng)的類(lèi)別。

3 實(shí)驗(yàn)及結(jié)果

實(shí)驗(yàn)環(huán)境為Windows 7 操作系統(tǒng)、lntel奔騰E5400（2.7GHz）雙核處理器、2GB內(nèi)存。實(shí)驗(yàn)中的算法都是基于MATLAB R2010a平臺(tái)開(kāi)發(fā)。

3.1 實(shí)驗(yàn)數(shù)據(jù)

本文的所有實(shí)驗(yàn)數(shù)據(jù)均來(lái)自UCI標(biāo)準(zhǔn)數(shù)據(jù)庫(kù)（http：／／archive.ics.uci.edu／ml／datasets.html）。表1中列出了實(shí)驗(yàn)所用數(shù)據(jù)集。由于目前尚未有公開(kāi)的不確定性數(shù)集，針對(duì)不確定性數(shù)據(jù)的實(shí)驗(yàn)都需在確定數(shù)據(jù)集上引入不確定性信息。方法如下：

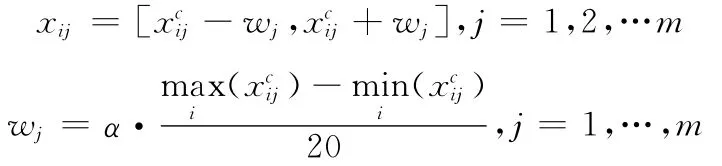
其中，maix與miin的差值表示數(shù)據(jù)集第j維屬性分布區(qū)間的大小，α控制實(shí)驗(yàn)所添加噪聲大小范圍的參數(shù)。

實(shí)驗(yàn)數(shù)據(jù)集見(jiàn)表1。

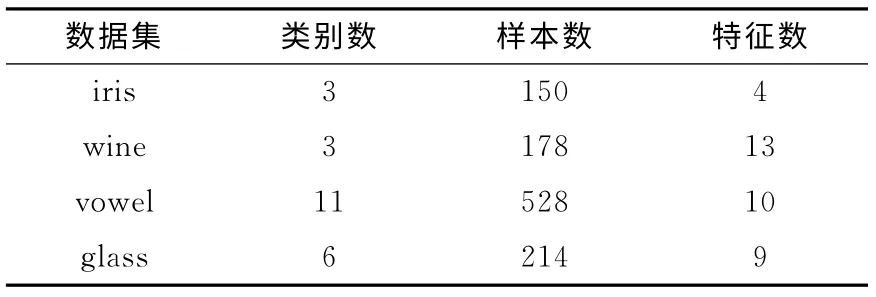
表1 實(shí)驗(yàn)數(shù)據(jù)集

3.2 實(shí)驗(yàn)設(shè)置

為了分析IUHSVM 算法的分類(lèi)精度及訓(xùn)練速度，本文進(jìn)行了3組仿真實(shí)驗(yàn)。

3.2.1 實(shí)驗(yàn)一

實(shí)驗(yàn)一為驗(yàn)證IUHSVM 方法對(duì)區(qū)間不確定性信息的抗干擾能力，實(shí)驗(yàn)采用iris、wine、vowel和glass這4組數(shù)據(jù)集，先測(cè)試SVM 和HSVM 方法對(duì)精確數(shù)據(jù)集的分類(lèi)精度作為比較對(duì)象，接著對(duì)實(shí)驗(yàn)數(shù)據(jù)集添加區(qū)間不確定性信息，驗(yàn)證IUHSVM 算法對(duì)區(qū)間不確定性數(shù)據(jù)的分類(lèi)精度，并與針對(duì)區(qū)間不確定性數(shù)據(jù)的樸素貝葉斯方法 （NBU1［5］和FBC［6］）的分類(lèi)精度進(jìn)行了比較。由于基于隨機(jī)理論的不確定性支持向量機(jī)方法［8，10］在數(shù)據(jù)的獲取、表示及描述模型上與非概率不確定性數(shù)據(jù)有較大區(qū)別，所以實(shí)驗(yàn)并未與該類(lèi)方法進(jìn)行比較。實(shí)驗(yàn)采用徑向基核函數(shù)

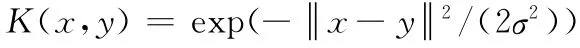
實(shí)驗(yàn)參數(shù)設(shè)定：實(shí)驗(yàn)數(shù)據(jù)集的每個(gè)樣本隨機(jī)設(shè)定區(qū)間不確定參數(shù)α∈［0.5，2］；懲罰參數(shù)取值范圍為C ＝［2－1，20，…，24］；徑向基參數(shù)的取值范圍為σ＝［2－1，20，…，24］。并記錄不同參數(shù)組合下最好的分類(lèi)結(jié)果。為驗(yàn)證算法的穩(wěn)定性，實(shí)驗(yàn)采用5折交叉驗(yàn)證 （5－fold cross validation）估計(jì)算法分類(lèi)精度：對(duì)每一數(shù)據(jù)集，將數(shù)據(jù)集隨機(jī)分為5組，輪流選擇其中一組作為測(cè)試集，其它4組作為訓(xùn)練集，取5次結(jié)果的均值作為最終估計(jì)精度，實(shí)驗(yàn)結(jié)果見(jiàn)表2。

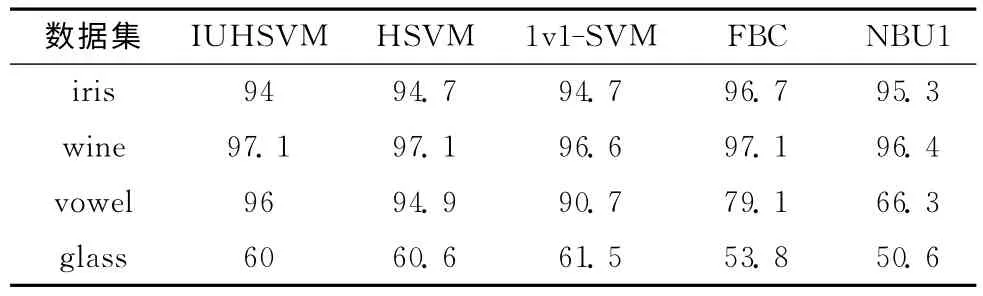
表2 不同算法的分類(lèi)準(zhǔn)確度／%

從表2中可以看出，對(duì)添加不確定性信息的數(shù)據(jù)集分類(lèi)的IUHSVM 方法與對(duì)精確數(shù)據(jù)集分類(lèi)的HSVM 方法分類(lèi)精度較接近，這表明IUHSVM 方法對(duì)非概率不確定性噪聲具有一定的抗干擾能力；同不確定性數(shù)據(jù)的樸素貝葉斯方法相比，IUHSVM 方法具有較優(yōu)的分類(lèi)精度和魯棒性，針對(duì)vowel和glass數(shù)據(jù)集，IUHSVM 方法的分類(lèi)精度比FBC方法分別高16.9%和6.2%；比NBU1分別高29.7%和9.4%。實(shí)驗(yàn)結(jié)果表明：IUHSVM 算法具有一定克服不確定性噪聲的能力，且具有良好的分類(lèi)精度和魯棒性，適用于區(qū)間不確定性數(shù)據(jù)的分類(lèi)問(wèn)題。

3.2.2 實(shí)驗(yàn)二

實(shí)驗(yàn)二測(cè)試IUHSVM 算法在不同迭代次數(shù)下目標(biāo)函數(shù)的收斂情況，實(shí)驗(yàn)數(shù)據(jù)集同實(shí)驗(yàn)一，實(shí)驗(yàn)結(jié)果如圖1所示。

在圖1中，各曲線分別表示構(gòu)造某一類(lèi)別超球面時(shí)，迭代次數(shù)與目標(biāo)函數(shù)的關(guān)系 （如iris數(shù)據(jù)集有3個(gè)類(lèi)別的數(shù)據(jù)，因此有3條曲線）。從圖中可以看出，4個(gè)數(shù)據(jù)集的目標(biāo)函數(shù)全都在第2次迭代時(shí)波動(dòng)較大，之后趨于穩(wěn)定 （部分曲線處于微小波動(dòng)狀態(tài)，其原因是上下兩層子規(guī)劃的交替迭代求解方法屬于非光滑優(yōu)化算法［18］）。實(shí)驗(yàn)數(shù)據(jù)集幾乎都在5次內(nèi)到達(dá)收斂條件，因此可通過(guò)設(shè)置較小的最大迭代次數(shù)來(lái)控制算法的計(jì)算復(fù)雜度。實(shí)驗(yàn)結(jié)果表明，基于超球支持向量機(jī)的IUHSVM 方法具有快速的迭代收斂速度，計(jì)算效率高。

3.2.3 實(shí)驗(yàn)三

圖1 迭代次數(shù)與目標(biāo)函數(shù)收斂情況

實(shí)驗(yàn)三測(cè)試IUHSVM 算法在執(zhí)行時(shí)間上的性能，并與針對(duì)精確數(shù)據(jù)且采用主流多分類(lèi)的1v1－SVM、1vr－SVM 方法進(jìn)行了比較。實(shí)驗(yàn)采用Vowel數(shù)據(jù)集，包含了528個(gè)樣本，共有11個(gè)類(lèi)別，樣本的屬性維數(shù)為10。實(shí)驗(yàn)分別選取Vowel中的m 類(lèi)數(shù)據(jù)進(jìn)行分類(lèi)，并記錄不同類(lèi)別數(shù)下的訓(xùn)練速度，實(shí)驗(yàn)結(jié)果如圖2所示。

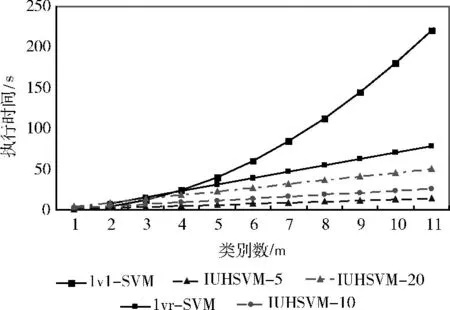
圖2 樣本類(lèi)別數(shù)與訓(xùn)練時(shí)間關(guān)系

從圖2可以看出，隨著樣本類(lèi)別的增加，1v1－SVM 的訓(xùn)練時(shí)間急劇增加，而1vr－SVM 和IUHSVM 方法的訓(xùn)練時(shí)間成正比增加。IUHSVM 方法采用迭代策略，但即使在最大迭代次數(shù)分別為5、10、20的情況下，執(zhí)行時(shí)間都低于其它兩種方法，尤其是設(shè)置最大迭代次數(shù)為5時(shí) （對(duì)應(yīng)圖2中最下面的線段），執(zhí)行時(shí)間的優(yōu)勢(shì)極為明顯。

實(shí)驗(yàn)結(jié)果表明：針對(duì)不確定性數(shù)據(jù)，即使IUHSVM 方法采用了迭代策略，但其執(zhí)行時(shí)間要遠(yuǎn)小于針對(duì)精確數(shù)據(jù)的標(biāo)準(zhǔn)SVM 主流多分類(lèi)器的執(zhí)行時(shí)間，即球結(jié)構(gòu)支持向量機(jī)具有遠(yuǎn)小于標(biāo)準(zhǔn)結(jié)構(gòu)SVM 的主流多分類(lèi)器的計(jì)算代價(jià)，適合不確定性數(shù)據(jù)分類(lèi) （往往具有高于精確數(shù)據(jù)的計(jì)算代價(jià)）的性能要求。

4 結(jié)束語(yǔ)

數(shù)據(jù)分類(lèi)的工程應(yīng)用中，常遇到區(qū)間形式的不確定性數(shù)據(jù)，而支持向量機(jī)是針對(duì)確定數(shù)據(jù)提出的二分類(lèi)方法，不能直接用于不確定性數(shù)據(jù)的分類(lèi)問(wèn)題。因此，提出了一種面向區(qū)間不確定性數(shù)據(jù)的分類(lèi)方法IUHSVM。該方法基于球結(jié)構(gòu)支持向量機(jī)，具有遠(yuǎn)高于基于標(biāo)準(zhǔn)結(jié)構(gòu)支持向量機(jī)的主流多分類(lèi)器方法的計(jì)算效率。仿真結(jié)果表明：針對(duì)區(qū)間不確定性數(shù)據(jù)，同基于樸素貝葉斯的FBC 和NBU1方法相比，IUHSVM 算法具有較優(yōu)的分類(lèi)精度和魯棒性，適用于多類(lèi)別的不確定性數(shù)據(jù)分類(lèi)問(wèn)題。

［1］Aggarwal CC，Yu PS.A survey of uncertain data algorithms and applications ［J］.IEEE Transactions on Knowledge and Data Engineering，2009，21 （5）：609－623.

［2］ZHOU Aoying，JIN Cheqing，WANG Guoren，et al.A survey on the management of uncertain data［J］.Chinese Journal of Computers，2009，32 （1）：1－16 （in Chinese）. ［周傲英，金澈清，王國(guó)仁，等.不確定性數(shù)據(jù)管理技術(shù)研究綜述 ［J］.計(jì)算機(jī)學(xué)報(bào)，2009，32 （1）：1－16.］

［3］REN Shijin.Interval number－based uncertain data mining and its applications ［D］.Hangzhou：Zhejiang University，2006（in Chinese）.［任世錦.基于區(qū)間數(shù)的不確定性數(shù)據(jù)挖掘及其應(yīng)用研究 ［D］.杭州：浙江大學(xué)，2006.］

［4］Tsang S，Kao B，Yip KY，et al.Decision trees for uncertain data［J］.IEEE Transactions on Knowledge and Data Engineering，2011，23 （1）：64－78.

［5］REN Jiangtao，LEE SD，CHEN Xialu，et al.Naive bayes classification of uncertain data［C］／／Ninth IEEE International Conference on Data Mining，2009：944－949.

［6］QIN Biao，XIA Yuni，WANG Shan，et al.A novel Bayesian classification for uncertain data ［J］.Knowledge－Based Systems，2011，24 （8）：1151－1158.

［7］QIN Biao，XIA Yuni，Prabhakar S，et al.A rule－based classification algorithm for uncertain data ［C］／／IEEE 25th International Conference on Data Engineering，2009：1633－1640.

［8］REN Zhiping，WANG Xiaojun，XU Menghui.Engineering structure uncertainty optimization design technology ［M］.Beijing：Science Press，2013 （in Chinese）. ［邱志平，王曉軍，許孟暉.工程結(jié)構(gòu)不確定性?xún)?yōu)化設(shè)計(jì)技術(shù) ［M］.北京：科學(xué)出版社，2013.］

［9］JIANG Chao.Theories and algorithms of uncertain optimization based on interval［D］.Changsha：Hunan University，2008（in Chinese）. ［姜潮.基于區(qū)間的不確定性?xún)?yōu)化理論與算法［D］.長(zhǎng)沙：湖南大學(xué)，2008.］

［10］YANG Jianqiang.Classification under input uncertainty with support vector machines ［D］.Southampton：University of Southampton，2009.

［11］DENG Shifei，QI Bingjuan，TAN Yanhong.An overview on theory and algorithm of support vector machine ［J］.Journal of University of Electronic Science and Technology of china，2011，40 （1）：2－10 （in Chinese）.［鄧世飛，齊丙娟，譚艷紅.支持向量機(jī)理論與算法研究綜述 ［J］.電子科技大學(xué)，2011，40 （1）：2－10.］.

［12］AI Qing，QIN Yuping，LI Yingchun.Multi－subjects text classification algorithm based on hyper－sphere support vector machines［J］.Computer Engineering and Design，2010，31（10）：2272－2275 （in Chinese）. ［艾青，秦玉平，李迎春.基于超球支持向量機(jī)的多主題文本分類(lèi)算法 ［J］.計(jì)算機(jī)工程與設(shè)計(jì)，2010，31 （10）：2272－2275.］

［13］LI Weixiang，LI Bangyi.Research in multiple classifications for interval number based on SVDD ［J］.Journal of Systems Science and Mathematical Sciences，2012，32 （3）：319－326（in Chinese）.［李為相，李幫義.一種基于支持向量域描述的區(qū)間數(shù)分類(lèi) ［J］.系統(tǒng)科學(xué)與數(shù)學(xué)，2012，32 （3）：319－326.］

［14］ZHAO Yinggang，CHEN Qi，HE Qingming.Fast learning algorithm for support vector domain description ［J］.Chinese Journal of Scientific Instrucment，2008 （z1）：798－800 （in Chinese）.［趙英剛，陳奇，何欽銘.基于支持向量域數(shù)據(jù)描述的快速學(xué)習(xí)算法［J］.儀器儀表學(xué)報(bào)，2008 （z1）：798－800.］

［15］Pistikopoulos EN，Dominguez L，Panos C，et al.Theoretical and algorithmic advances in multi－parametric programming and control［J］.Computational Management Science，2012，9 （2）：183－203.

［16］Suvrit Sra，Sebastian Nowozin，Stephen J Wright.Optimization for machine learning ［M］.Cambridge，MA：Mit Press，2012.