呼叫中心智能排班系統關鍵技術

夏正洪，潘衛軍

（中國民用航空飛行學院 空中交通管理學院，四川 廣漢618307）

0 引 言

科學地預測排班周期內的話務量水平和所需坐席數、合理地制定話務員的班次對于充分利用呼叫中心［1］現有資源，提高呼叫中心的服務水平和質量有重要意義。國內外話務量預測的基本方法有基于神經網絡［2，3］和基于支持向量機［4］的算法，坐席數預測通常采用Erlang＿C 公式［1］。牟穎等［5］對比了神經網絡算法和支持向量機算法用于大型呼叫中心話務量預測的有效性，謝傳柳等［1］在牟穎預測的話務量數據的基礎上，使用Erlang－C 公式預測所需坐席數，并選用粒子群算法［6］對坐席數曲線進行擬合，最后采用隊列輪循法生成了總班表和個人班表，基于J2EE開發了基于B/S模式的大型呼叫中心排班系統并得到了驗證和推廣［7］。曾俊［8］建立了話務量預測模型并進行了仿真分析；韓銳等［9］采用微分進化策略更好地預測了話務量；姚世紅［10］基于微正則算法和支持向量機的方法完成了對呼叫中心話務量預測。可見，話務量預測的準確性直接關系到后續坐席數預測的準確性，影響典型班次對應的人數預測結果的可靠性。個人每月上班總時間應體現高規律性和高公平性，總班表和個人班表的合理性是衡量智能排班系統是否有效的唯一標準。

呼叫中心智能排班系統通過對歷史話務量數據的分析，科學預測未來一段時間內的話務量水平及所需坐席數，結合呼叫中心的可用資源進行班次人數的制定，排班過程實質為將話務員進行合理分配的問題。本文闡述了呼叫中心智能排班系統的實現流程，分析了學習率和訓練精度對BP神經網絡的訓練最大次數、收斂時間和話務量預測精度的影響。根據呼叫中心數據日變化特點，提出并驗證了分時間段多次采用神經網絡比整體預測所得話務量結果更加準確。基于話務量預測結果使用Erlang－C 公式進行了坐席數的預測，定義典型班次后使用粒子群算法進行了班次人數的擬合。基于J2EE開發了呼叫中心智能排班系統，并完成對某呼叫中心可用資源的合理配置，實現了成本最小化和利潤最大化。

1 呼叫中心話務量預測

1.1 提高話務量預測精度

科學準確預測話務量是合理進行呼叫中心智能排班的前提，根據話務量預測結果進行所需坐席數的預測，再根據話務員數量、可用坐席數、班次等約束條件進行人員的分配和班表的生成。可見，話務量預測結果的精度直接影響坐席數預測的準確性和班表的可用性，是呼叫中心智能排班系統的核心基礎。根據呼叫中心歷史話務量的周期性特點，本文選用BP神經網絡來進行話務量的預測［4］。影響神經網絡模型預測精度的因素通常有樣本數據是否豐富、模型輸入參數的選擇、隱層層數和節點數的選取、學習率、最大循環次數、訓練精度等。其中，BP神經網絡隱層層數和節點數直接關系到網絡的收斂速度，最大循環次數和精度決定網絡模型的訓練時間，學習率決定神經網絡是否收斂以及收斂速度。因此，合理選擇BP神經網絡模型及其相關參數，提高話務量預測的精度是系統實現中的關鍵問題。

1.2 合理選擇BP神經網絡參數

本文使用某呼叫中心系統2010 年9 月到11 月的話務量作為訓練樣本，以 （00：01－00：29，00：30－00：59，……）半小時為單位的話務總量作為研究對象，得到話務量曲線的變化如圖1所示，其中X 軸是某月以半小時為間隔的時間段個數，如9月數據段個數為2＊24＊30＝1440，Y 軸是X 軸上每半小時的話務總量。可見，3 個月話務量曲線變化幾乎相同，呈現明顯的月周期性和日周期性。同時，每天的話務量數據在早晨10點到11點和晚上19點到20點間出現兩次峰值，且早峰值略大于晚峰值，在凌晨3點到5點話務量達到最低，與人的生理活動特征極為相符。因此，筆者使用BP神經網絡對歷史話務量進行訓練，輸入層、隱層、輸出層節點數分別為6、6、1；待神經網絡訓練完畢后記錄網絡中各層權重和偏倚值，并重現該網絡對12月的話務量數據進行預測。并將預測的話務量數據與12月份真實話務量數據進行比較，統計其預測精度的平均值，從而驗證BP神經網絡模型用于話務量的預測的有效性。

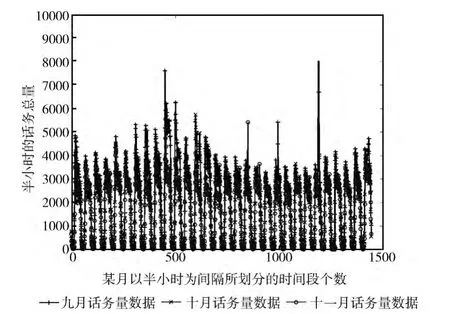
圖1 歷史話務量數據的月、日周期性

本文通過統計神經網絡的實際循環次數、收斂時間來描述訓練精度、學習率對神經網絡訓練收斂情況的影響見表1。可見，學習率大小直接影響神經網絡的實際循環次數和收斂時間，學習率越小，網絡循環次數越大，收斂所需時間越長。當學習率不變而訓練精度變小時，實際循環次數不再發生變化，收斂所需時間幾乎不變；而訓練精度不變的情況下，學習率變小會導致實際循環次數顯著增大，收斂時間顯著增長。從表中可以看出，話務量預測精度跟神經網絡的訓練精度直接相關，而學習率主要影響網絡的訓練次數和收斂時間。為了保證訓練精度的前提下盡量縮短網絡的收斂時間，本文選取BP 神經網絡的學習率為0.01，訓練精度為0.0001。

表1 學習率和訓練精度對神經網絡收斂的影響

1.3 分時間段預測話務量

根據呼叫中心話務量數據日變化特點，筆者提出了將2010年9月至11月的歷史話務量數據按時間段劃分，分別采用BP神經網絡進行訓練和預測。時間段分別為0點到5點、5點到10點、10點到20點、20點到24點。當神經網絡模型達到穩定狀態的時候，分別記錄下各模型中各層權重和偏倚值；然后再按時間段的不同分別重現神經網絡并預測12月第一周 （12月1日到7日）的話務量進行預測，將分段預測結果分別與原始數據和整體預測結果對比如圖2所示。其中，橫軸為12月第一周半小時為間隔的時間段數目即7＊24＊2＝336 個，縱軸為每半小時的話務量總數，數據系列1表示12月原始話務量變化曲線，數據系列2和3分別表示是整體采用神經網絡和分段采用神經網絡預測的話務量結果。

為了比較兩種方法的預測精度，將每半小時話務量預測結果分別減去真實話務量，并除以真實話務量得到每個

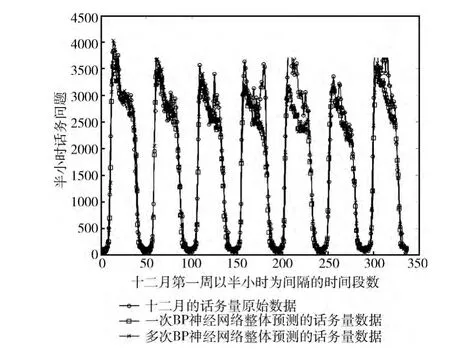
圖2 分段預測結果與整體預測、原始數據對比

數據的誤差errori，再將所有的誤差相加除以數據點個數得到平均誤差AverageError，從而論證分段預測結果和整體預測結果的優劣。其中，i的取值為 （1，2……，336），xi表示第i個時間段的話務量預測結果，而xi0表示該時間點的真實話務量。將單個數據點誤差進行對比如圖3所示，用數據系列1表示的分段預測結果較用數據系列2所表示的整體預測結果偏差小。利用公式 （2）得到整體預測和分段預測結果的平均誤差的絕對值分別為0.299907 和0.206771，即分時間段多次使用神經網絡的預測結果精度提高了9.3%

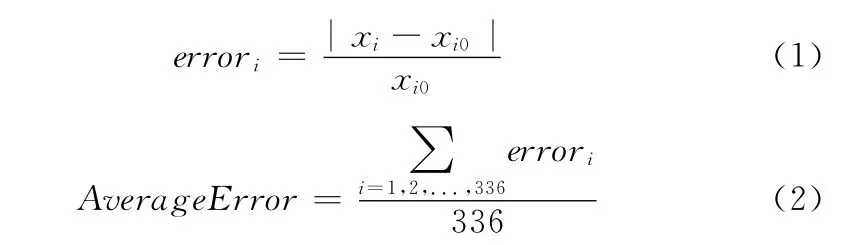
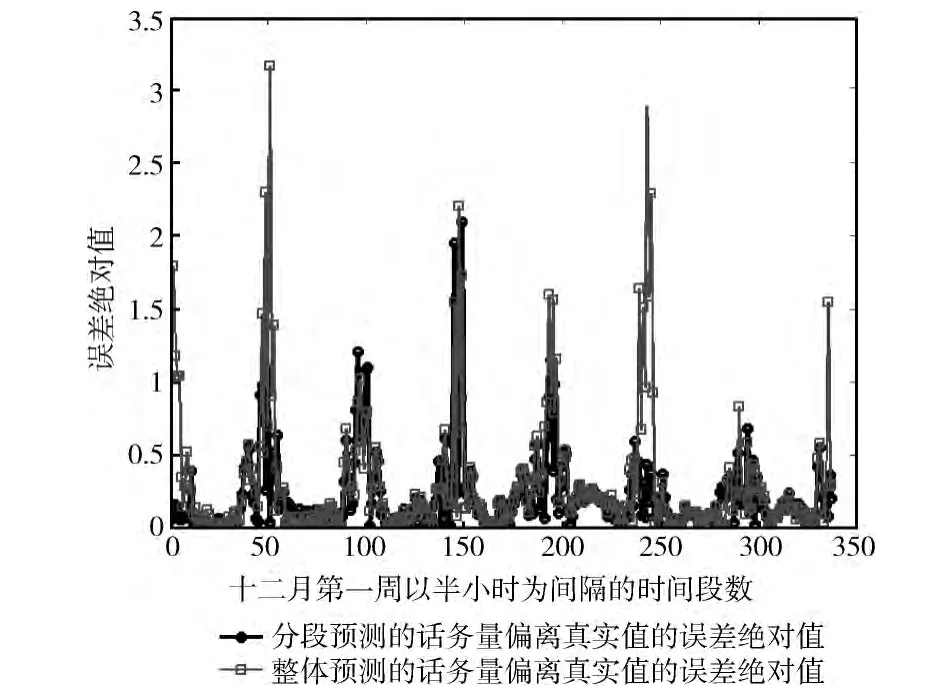
圖3 分段預測和整體預測結果誤差分析

2 呼叫中心班次人數預測

呼叫中心班次人數預測是基于所預測的話務量數據，使用Erlang－C公式預測坐席數［1，4］，并基于所定義的典型班次、規定的服務水平等參數進行坐席數曲線擬合，得到每個典型班次所對應的話務員數量。

2.1 基于Erlang－C的坐席數預測

假設以每半小時為單位的話務量的平均客戶呼入率為λ，平均話務持續時間為Ts，呼叫中心可用客服總人數為m，則半小時的話務流量數據為μ，座席占用率為ρ，Ec（m，μ）表示話務不能馬上被處理而必須等待的概率，話務在目標等待時間內被處理的概率為Wt。根據歷史話務量數據日變化特征，基于分時間段神經網絡模型預測的結果，本文假設呼叫中心可用話務員人數為650，可用坐席數為450，各時間段滿意服務水平分別為0.75，0.8，0.8，0.75；且目標等待時間為20s，每個話務量平均持續時間為160s，坐席占用率均為80%。根據Erlang－C 公式，在最大客服人數范圍內找到第一個滿足該時間段服務水平的坐席數值，即半個小時內所需的話務員數量如圖4中的預測所需坐席數據系列所示

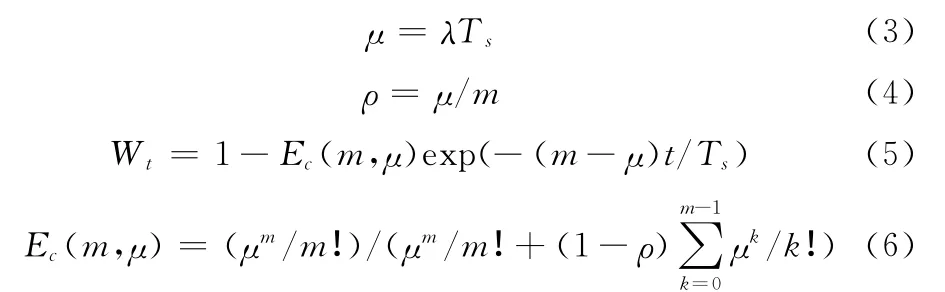
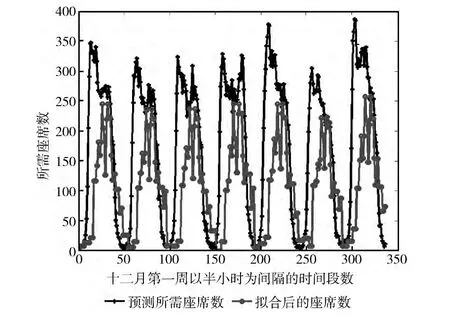
圖4 坐席數曲線擬合

2.2 坐席數曲線擬合

坐席數曲線擬合的原則是保證全局的服務水平達到給定的值，坐席數曲線擬合的實質是一個多約束最優化問題，必須考慮呼叫中心的話務員數量、坐席數，此外還必須考慮員工的休息，上班時長等因素。要對呼叫中心人力資源進行合理配置，單獨考慮坐席數點是沒有任何意義的，因為班次制定不可能以半小時作為員工的工作時長。因此，制定呼叫中心的合理典型班次是進行坐席數曲線的前提根據文獻 ［1］所制定的典型班次，基于坐席數預測結果使用粒子群算法進行坐席數擬合即可得到各典型班次時間段內滿足平均服務水平所需的話務員數量如圖4 所示。其中，數據系列1為預測的所需坐席數，數據系列2為實際分配的坐席數，X 軸為十二月第一周以半小時為間隔的時間段個數，Y 軸為所需的坐席數，擬合之后的坐席數在該排班周期內的平均服務水平位0.805。值得注意的是，如果一個班次的工作時間由兩個及以上的不同時間段組成 （即一個班次中間有間斷的情況），其工作時長不等于結束時間與開始時間之差；若直接運用于粒子群算法中，將導致在班次時間間隔內的服務水平達不到預期的值。同時，雖然這種班次的工作時間不連續，但是上班的人數以及上班人員是不會發生變化的。因此，可以將不同時間段的小班視為獨立的班次帶入粒子群算法中，并且通過標志位來確定相同班次，運算過程中保證班次相同的班有相同的人數和人員，這樣才可能在達到滿意的服務水平的前提下生產合理可用的班表。

3 呼叫中心智能排班系統的實現

呼叫中心排班系統通過科學地預測排班周期內的話務量和所需坐席數，合理安排話務員的數量和班次，實現保障客戶服務水平前提下的完成呼叫中心資源的合理配置［10］。為了保證呼叫中心話務員上班的高規律性和高公平性，本文通過引入 “休息班”到智能排班算法中；考慮到話務員以班組為單位來進行排班安排的，本文采用隊列輪循法來實現總班表和個人班表的生成，將一個班組的員工裝入隊列中，定義N 個班次和隊列，將隊列進行首尾串聯，然后以天為單位將隊列中的員工作一次循環，最終得到排班周期內的總班表和個人班表。如圖5所示，呼叫中心智能排班系統實現流程：根據呼叫中心歷史話務量數據的周期性特點，選用BP神經網絡對歷史話務量進行分時間段多次訓練，待網絡自主學習完畢后保存網絡的權重和偏倚值，并對排班周期內的話務量數據進行預測；結合所設置的項目組服務水平參數，使用Er＿langC 公式進行所需坐席數預測，并計算所求話務量和坐席數對應的平均服務水平、平均通話時長、員工利用率等。通過制定項目組典型班次，結合項目組客服總數、坐席總數等信息采用粒子群算法預測班次所需人數。最后，由于話務員是上班或休息是以班組為單位，因此必須將班次人數預測結果轉換為每個班次所需的班組數，并提供對班組、班組成員關系的管理，最終生成排班周期內的總班表和個人班表分別如圖6 和圖7所示。

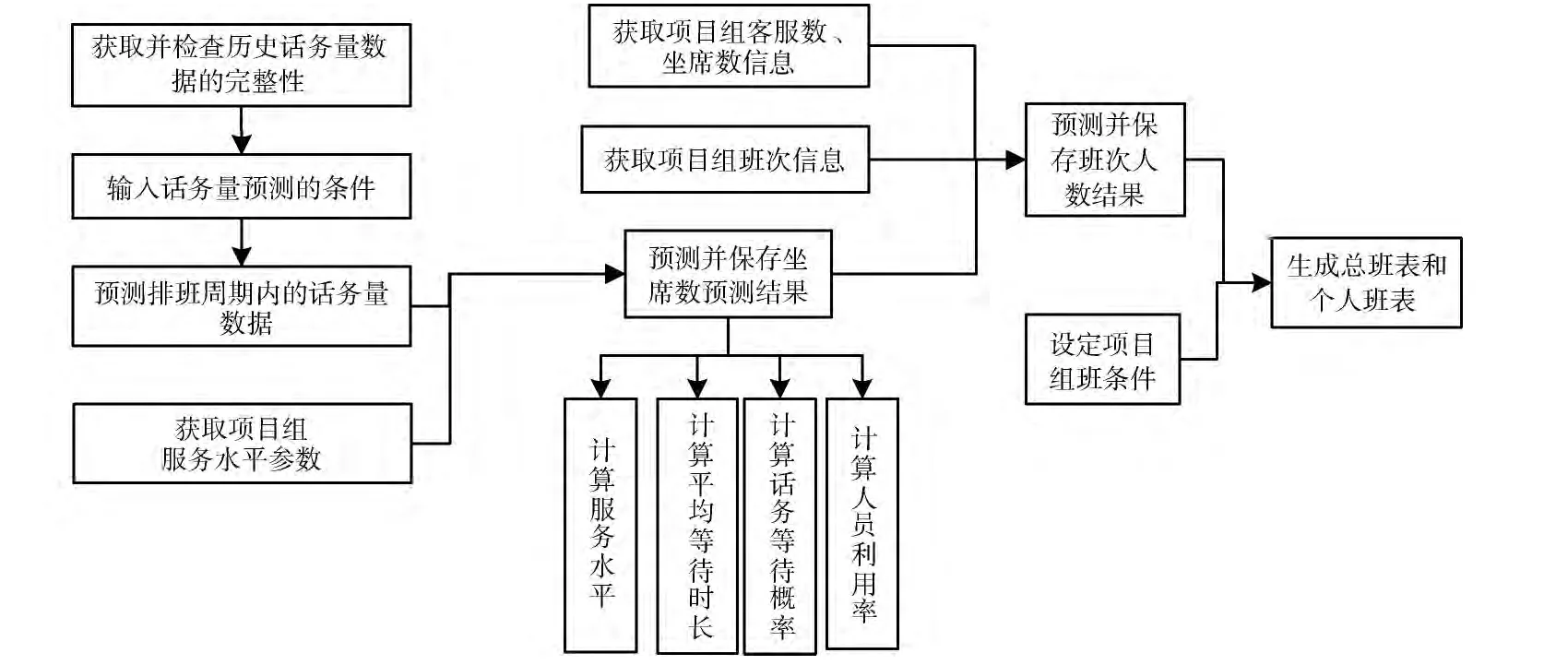
圖5 呼叫中心智能排班系統的實現流程

圖6 排班周期內的總班

圖7 排班周期內的個人班

4 結束語

本文提出了大型呼叫中心智能排班系統設計的關鍵技術問題，著重討論如何提高話務量預測結果的精度和進行坐席數曲線的擬合。根據話務量數據的日周期性和日變化性特點，提出并驗證了分時間段分別采用多次神經網絡模型進行訓練和預測的可行性和合理性。基于話務量預測結果使用Erlang－C公式得到需求的坐席數，定義了呼叫中心的典型班次并使用粒子群算法進行了班次人數曲線的擬合；開發了呼叫中心智能排班系統，結合呼叫中心可用資源進行了合理的排班，在保證服務水平和質量的前提下完成了呼叫中心資源的合理配置。

［1］XIE Chuanliu，WANG Junfeng，XIA Zhenghong.Research on crew rostering algorithm of large－scale call center ［J］.Computer Engineering and Design，2010，31 （23）：5108－5113 （in Chinese）.［謝傳柳，王俊峰，夏正洪.大型呼叫中心排班算法的研究 ［J］.計算機工程與設計，2010，31 （23）：5108－5113.］

［2］MA Man.Application and research of neural network in traffic prediction ［D］.Changchun：Jilin University of China，2009（in Chinese）. ［馬曼.神經網絡在話務量預測中的應用研究［D］.長春：吉林大學，2009.］

［3］YAO Yuehua，NIU Yuanyuan.Consumer price index prediction based on RBF neural network ［J］.Computer Applications and Software，2010，27 （10）：92－94 （in Chinese）.［姚躍華，牛園園.基于RBF神經網絡的CPI預測 ［J］.計算機應用與軟件，2010，27 （10）：92－94.］

［4］CHEN Dianbo.Traffic forecasting methods of support vector machines ［D］.Changsha：Central South University，2008（in Chinese）.［陳電波.基于支持向量機的電信話務量預測方法 ［D］.長沙：中南大學，2008.］

［5］MOU Ying，XIE Chuanliu，XIA Zhenghong.Forecast on traffic of large call center［J］.Computer Engineering and Design，2010，31 （21）：4686－4690 （in Chinese）.［牟穎，謝傳柳，夏正洪.大型呼叫中心話務量預測 ［J］.計算機工程與設計，2010，31 （21）：4686－4690.］

［6］YE Chunming，PAN Deng，PAN Fengshan.Critical chain project management based on chaos particle swam optimization［J］.Application Research of Computers，2011，28 （3）：889－891 （in Chinese）.［葉春明，潘登，潘逢山.基于混沌粒子群算法的關鍵鏈項目進度管理研究 ［J］.計算機應用研究，2011，28 （3）：889－891.］

［7］Xie Chuanliu，Wang Junfeng，Mou Ying.The design and implementation of large－scale call center management system ［C］//3rd International Conference on Computational Intelligence and Industrial Application，2010：116－119.

［8］ZENG Jun.Modeling and simulation on communication traffic forecasting model［J］.Computer Simulation，2012，29 （2）：116－119 （in Chinese）.［曾俊.話務量預測模型的建立和仿真研究 ［J］.計算機仿真，2012，29 （2）：116－119.］

［9］HAN Rui，JIA Zhenhong.Telephone traffic load prediction based on SVR with DE－strategy ［J］.Computer Engineering，2011，37 （2）：178－180 （in Chinese）. ［韓銳，賈振紅.基于SVR 與微分進化策略的話務量預測 ［J］.計算機工程，2011，37 （2）：178－180.］

［10］YAO Shihong，WANG Tao，JIA Zhenhong.Algorithm of microcanonical－SVM based for forecasting traffic load ［J］.Computer Engineering and Applications，2012，48 （3）：105－107 （in Chinese）.［姚世紅，王濤，賈振紅.基于微正則算法和支持向量機的話務量預測 ［J］.計算機工程與應用，2012，48 （3）：105－107.］