MCS自適應算法在非線性結構AMD控制中的應用*

涂建維，張妙嫻，汪伯潮

(武漢理工大學道路橋梁與結構工程湖北省重點實驗室，湖北武漢430070)

0 引言

工程結構在地震、強風等災害荷載作用下，會進入彈塑性階段，結構抗力會發生衰減，呈現出一系列復雜的非線性問題 (秦榮，2006)。當結構遭遇較強地震作用時，結構構件將有可能發生屈服、結構剛度發生退化，從而使結構響應迅速增大，甚至造成結構破壞、倒塌 (韓建平等，2007)。結構AMD主動控制技術使得結構在外部動力荷載作用下，能主動調整結構參數，從而最優地減小結構振動響應。控制算法作為該技術的核心組成部分，決定著振動控制的穩定性和減振效果的好壞。因此，選擇合適的控制算法對AMD系統能否有效減小非線性結構的振動響應是極為重要的。

最小控制綜合 (MCS)算法最早由Stoten和Benchoubane(1990a，b)提出，通過對操縱器、蓄水庫裝置進行仿真、試驗研究，證明了MCS算法在系統參數變化、外部干擾不確定以及系統非線性的情況下也能達到很好的控制效果;Stoten和Gomez(2001)運用MCS算法控制振動臺，證明了MCS算法通過自適應增益的實時調整，可以有效地處理振動臺運行過程中出現的非線性情況，提高振動臺的精度。

基于以上研究成果，本文將MCS算法應用于AMD控制系統中，系統研究了該控制系統對非線性結構的控制效果。本文比較了剛度退化結構與線性結構的地震反應;用MCS算法來控制AMD系統，采用拉格朗日法推導了地震作用下結構自適應控制的基本方程;為了驗證MCS算法控制AMD裝置的有效性，在小型振動臺上對安裝AMD系統的剛度突變結構進行試驗研究。

1 非線性結構的地震反應仿真

本文研究對象是安裝AMD控制系統的單層結構模型，模型簡圖如圖1所示，具體參數如表1所示。

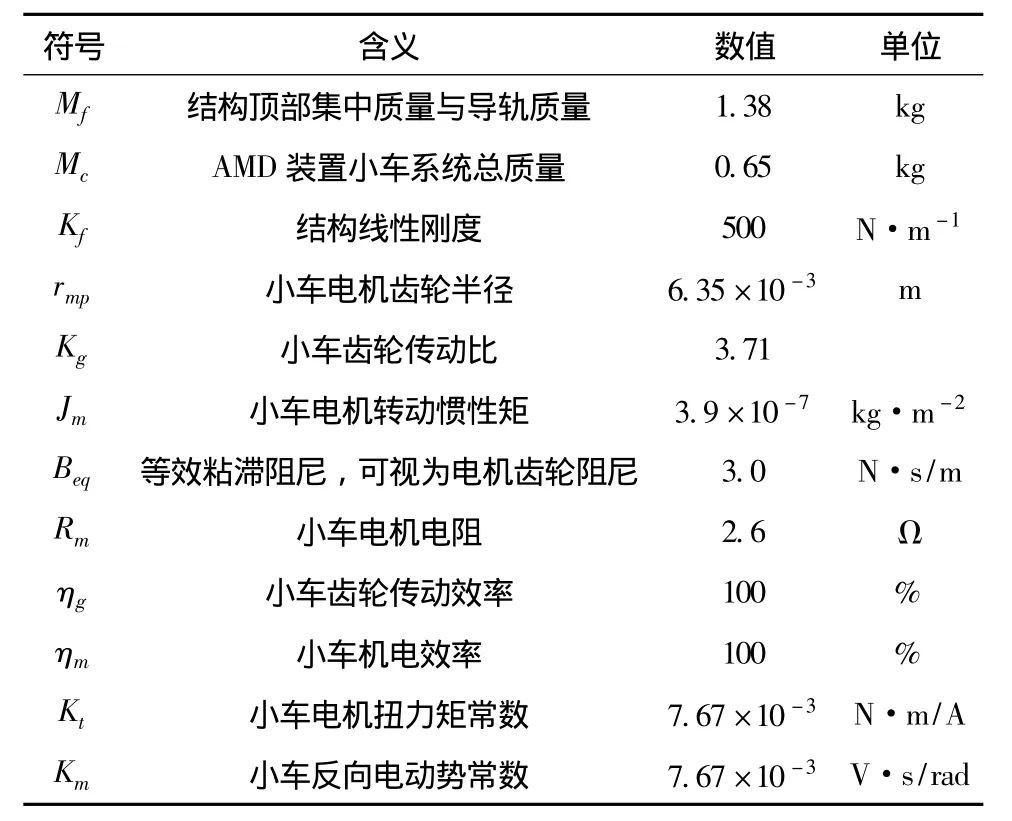
表1 AMD裝置控制的結構模型參數Tab.1 The model parameters of the structure under AMD control

首先采用理想不退化雙線型模型建立結構剛度的退化模型 (彭凌云，2004)，如圖2所示。該模型的加載剛度和卸載剛度均為結構初始剛度，結構初始剛度k1=500 N·m-1，屈服位移xy=10 mm。當結構位移x≥xy時，結構屈服進入彈塑性階段，剛度退化為k2，取k2=0.1，k1=50 N·m-1。在SIMULINK中對無控結構進行非線性仿真分析，地震波選用壓縮后的El Centro波，得到結構的滯回曲線和結構剛度隨時間的變化如圖3所示。

圖1 結構振動的AMD主控控制模型Fig.1 AMD control model of structural vibration

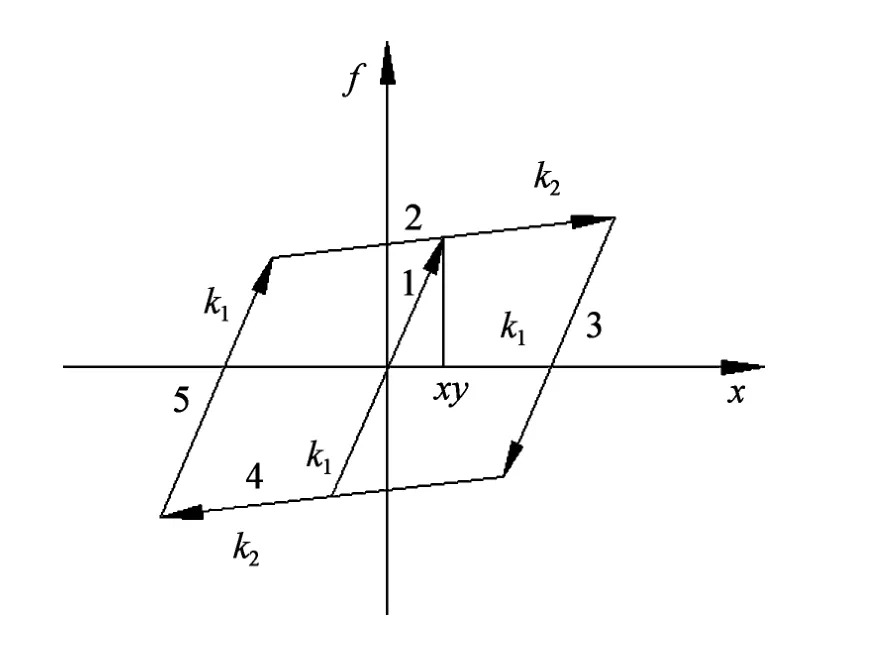
圖2 雙線型模型Fig.2 Double linear model

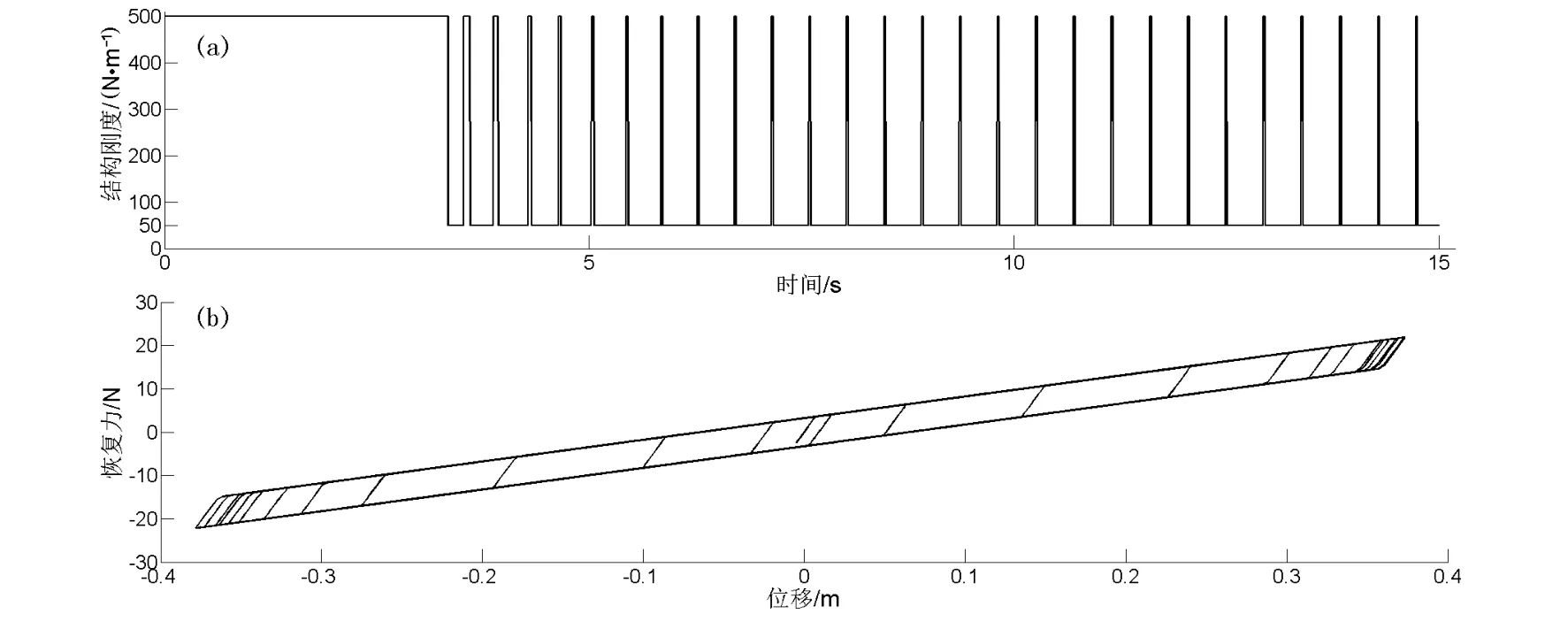
圖3 無控結構剛度的時程曲線 (a)和滯回曲線 (b)Fig.3 The time history(a)and hysteretic(b)curves of uncontrolled structure stiffness

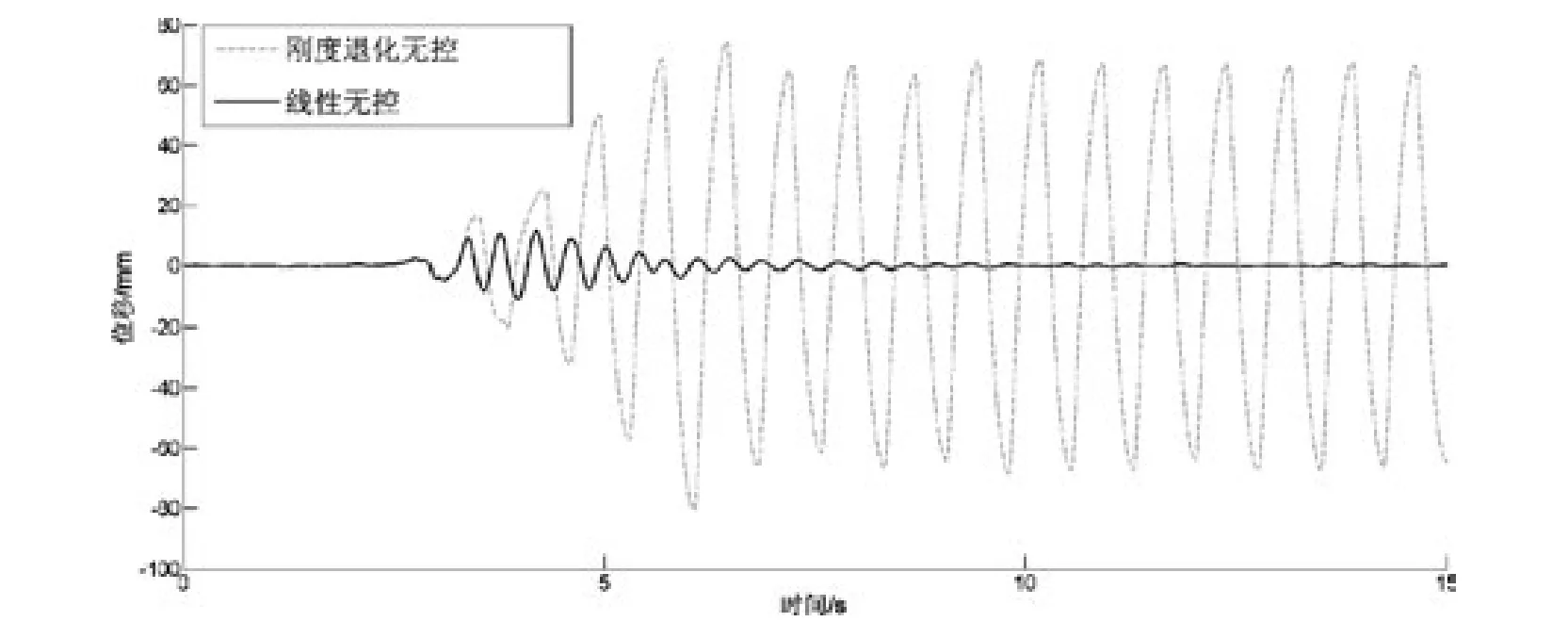
圖4 無控結構位移響應的時程曲線Fig.4 The time history of uncontrolled structural displacement response

從圖3可以看到，結構恢復力與位移之間表現出明顯的不退化雙線型恢復力模型，說明仿真過程是準確無誤的;圖4對比了線性無控與剛度退化時的結構位移響應，從圖中可以看到，由于沒有減振裝置，結構剛度從第三秒開始就處于屈服退化狀態，結構響應迅速增大并持續保持在較大范圍內波動，這會威脅到結構的安全，需要采取減振措施對結構響應進行控制。

2 基于MCS算法的結構AMD系統控制方程

首先闡述AMD系統控制的原理及公式。結構AMD主動控制系統由傳感器、控制器和作動器組成，其原理如圖5所示。在整個控制過程中，需要實現控制力可以實時改變和受控結構的實際振動響應與參考模型響應保持一致這兩個目標 (歐進萍，2003)，參考模型MCS自適應控制算法可以實現上述目標，其原理如圖6所示。受控結構在外部激勵d(t)作用下輸出響應為X(t)，參考模型在外部激勵r(t)作用下輸出響應為Xm(t)。將Xm(t)作為目標響應，Xe(t)為X(t)與Xm(t)產生的偏差，它會驅動自適應控制器，計算當前時刻的自適應增益K(t)和Kr(t)，從而實時計算出主動控制力U(t)。將U(t)將施加到受控結構上，會使得結構實際響應跟蹤目標響應，即X(t)=Xm(t)，從而實現了控制目標。

在地震作用下，結構振動的AMD主動控制模型如圖1所示，其拉格朗日方程為 (盧圣治，2004)

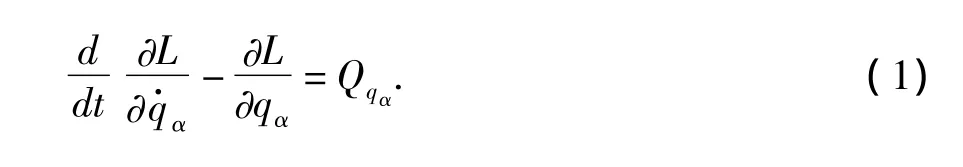
其中，L為系統的拉格朗日函數，L=T-V，V是系統的勢能，T是系統的動能;qα是廣義坐標，本文廣義坐標取xf和xc;Qqα是對應廣義坐標上的廣義力。

在絕對位移坐標系下，地震作用的地面位移為xg(t)，由式 (1)可以得到:

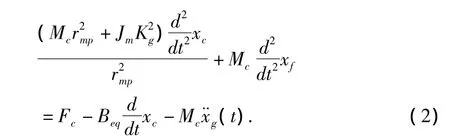
圖5 結構AMD主動控制系統Fig.5 AMD control system of the structure

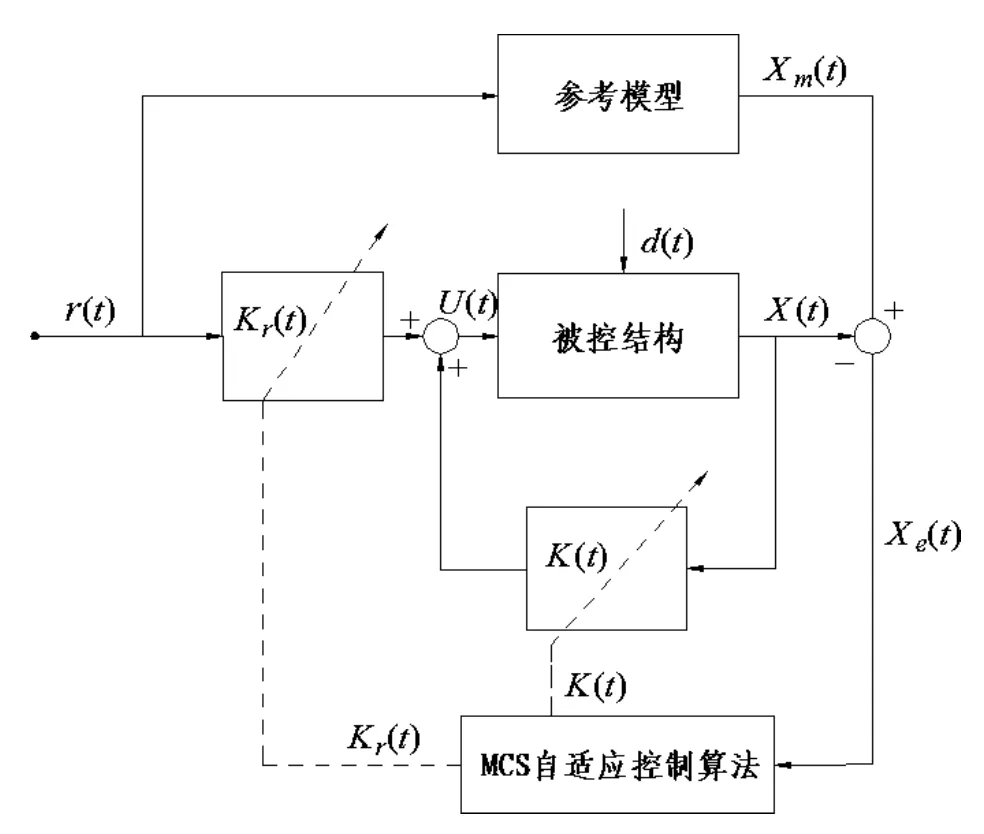
圖6 MCS自適應算法控制流程圖Fig.6 The control flow chart of MCSadaptive algorithm

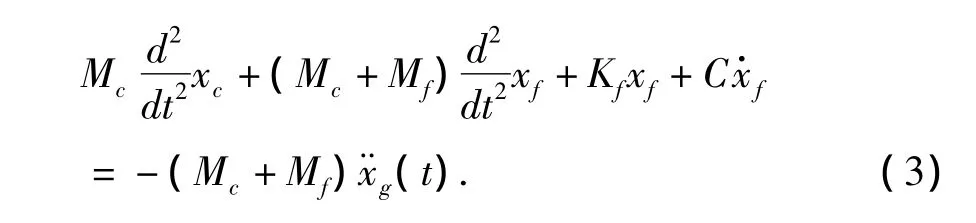
其中，Jm為小車電機轉動慣性矩;Kg為小車齒輪傳動比;rmp為小車電機齒輪半徑;Beq為小車等效粘滯阻尼;C為結構阻尼。

其中，d(t)=x¨g(t)，對于采用MCS控制算法的結構AMD控制系統，主動控制力U可由式 (5)計算得到:

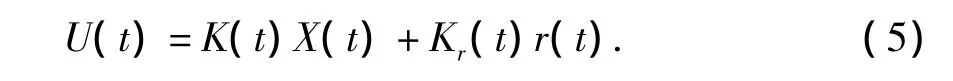
其中，r(t)為參考輸入，取r(t)=Kd·d(t)=Kd·x¨g(t)，0 ＜Kd＜ 1，K(t)、Kr(t)為自適應增益，可通過式 (6)計算得到:

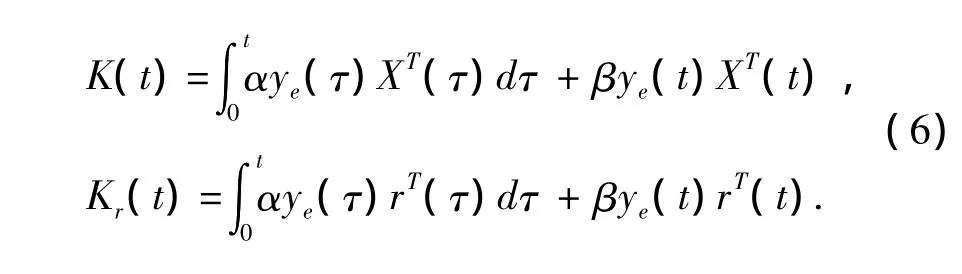
其中，比例因子α＞0，β≥0;ye(t)是系統輸出誤差信號，可由式 (7～8)計算得到:

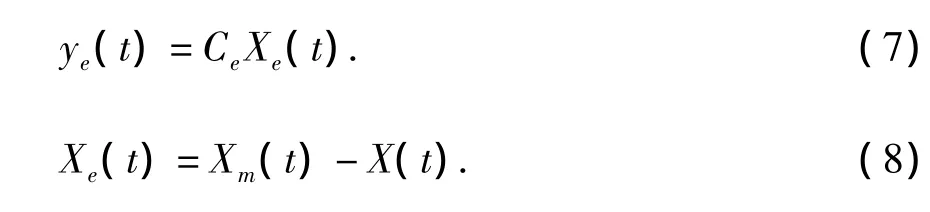
其中，Ce是輸出矩陣;Xe(t)是參考模型輸出與被控模型輸出的誤差;Xm(t)是參考模型的輸出響應。這幾個參數可通過以下參考模型的狀態方程求得:

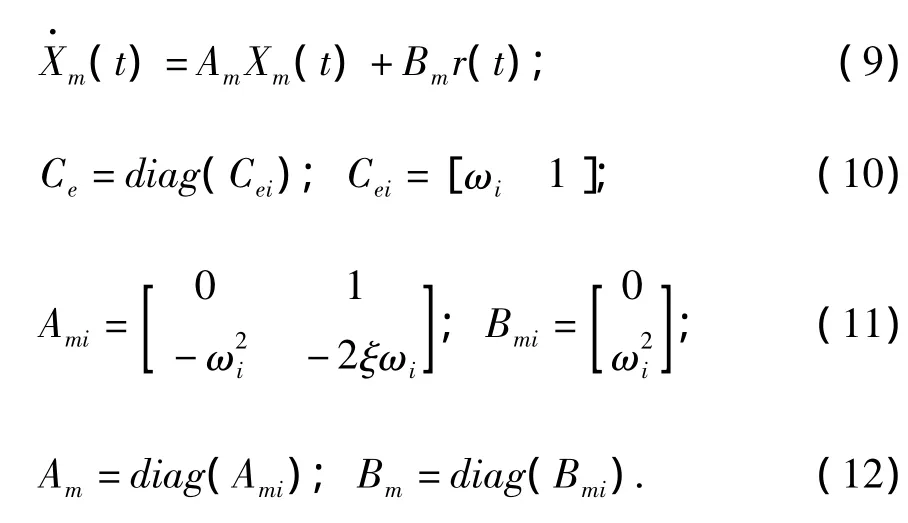
其中，ωi為結構第i階自振頻率 (i=1，2，…，n);ξ為結構阻尼比。

3 MCS算法對剛度突變結構的控制試驗

該試驗在武漢理工大學完成，試驗裝置由小型振動臺、一層剪切型鋼框架結構和AMD控制裝置組成，加拿大Quanser公司研發了該設備。為了實現結構的剛度突變，先對結構采用增加橡皮筋斜撐的方法來增加結構剛度，如圖7所示。當結構在振動過程中突然剪斷張緊的橡皮筋，這樣結構的剛度會突然減小以實現結構的剛度突變。剪斷橡皮筋后的結構剛度以及其余參數如表1所示。

圖7 加橡皮筋的試驗結構Fig.7 Experimental structure of the added rubber bands

使用壓縮后的El Centro波作為地震激勵驅動小型振動臺，地震波的峰值加速度是0.5 g，持續時間是13.4 s，取實測臺面加速度作為d(t)，采用降低地震能量方法建立參考模型 (張凱靜等，2010)，地震能量調節增益Kd=0.75，采用MCS自適應算法對AMD裝置實施控制，輸出矩陣取Ce=［ω11］=［17.8 1］，α =100，β=10。

圖8顯示了剪斷橡皮筋前后結構的位移響應。從圖中可以看出，在地震持續時間為2.8 s時，皮筋被剪斷，結構的剛度從643 N·m-1迅速減小到500 N·m-1，相對于不剪斷皮筋情況結構頂點的最大位移從13 mm增大到20 mm。特別是在剪斷皮筋的瞬間，結構的最大位移從9 mm迅速突變到20 mm，增大了約120%。圖9顯示了剛度突變情況下無控、MCS算法控制的結構的位移響應。從圖中可以看出，采用MCS算法的AMD系統可以有效地減小結構的振動響應，具體如表2所示。其中，xf、x¨f分別是結構頂部相對于地面的位移和加速度;magxf是結構位移傅里葉幅值;xf，RMS是結構位移均方根值，表示在地震作用持續時間內xf各瞬時值的平方的平均值的平方根。在地震持續時間為2.8 s皮筋被剪斷的瞬間，MCS算法可以將結構位移從無控狀態的20 mm減小到7 mm。這是因為MCS自適應算法是根據結構響應與參考模型響應的誤差反饋實時地改變控制增益，因此當結構響應發生突變時，MCS算法也可以迅速增大控制增益來得到較大的控制電壓，從而可以很好地減小結構振動響應。

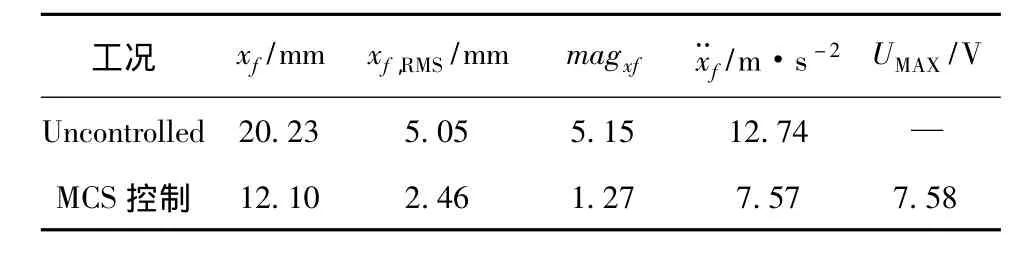
表2 地震作用下的試驗結構振動響應Tab.2 The vibration responses of experimental structure under earthquake

圖10比較了參考模型輸出的位移響應和實際結構的位移響應。從圖中可以看到，即使結構剛度發生突變，實際位移也能夠很好的逼近參考模型的輸出響應，達到預期的減振效果。

4 結論

研究了MCS自適應控制算法對非線性結構的AMD主動控制，并完成了剛度發生突變的單自由度結構的振動臺試驗。仿真和試驗結果表明:MCS算法是一種優良的自適應控制算法，將它應用到結構AMD控制系統中，可以有效地減小結構響應。在結構發生剛度突變時，MCS算法通過自適應參數的實時調整仍能有效地控制AMD裝置，使結構實際輸出響應與參考模型輸出保持一致，達到預期的減振效果。

圖8 剛度突變前后的結構位移時程Fig.8 The time history of structure displacement before and after stiffness mutation

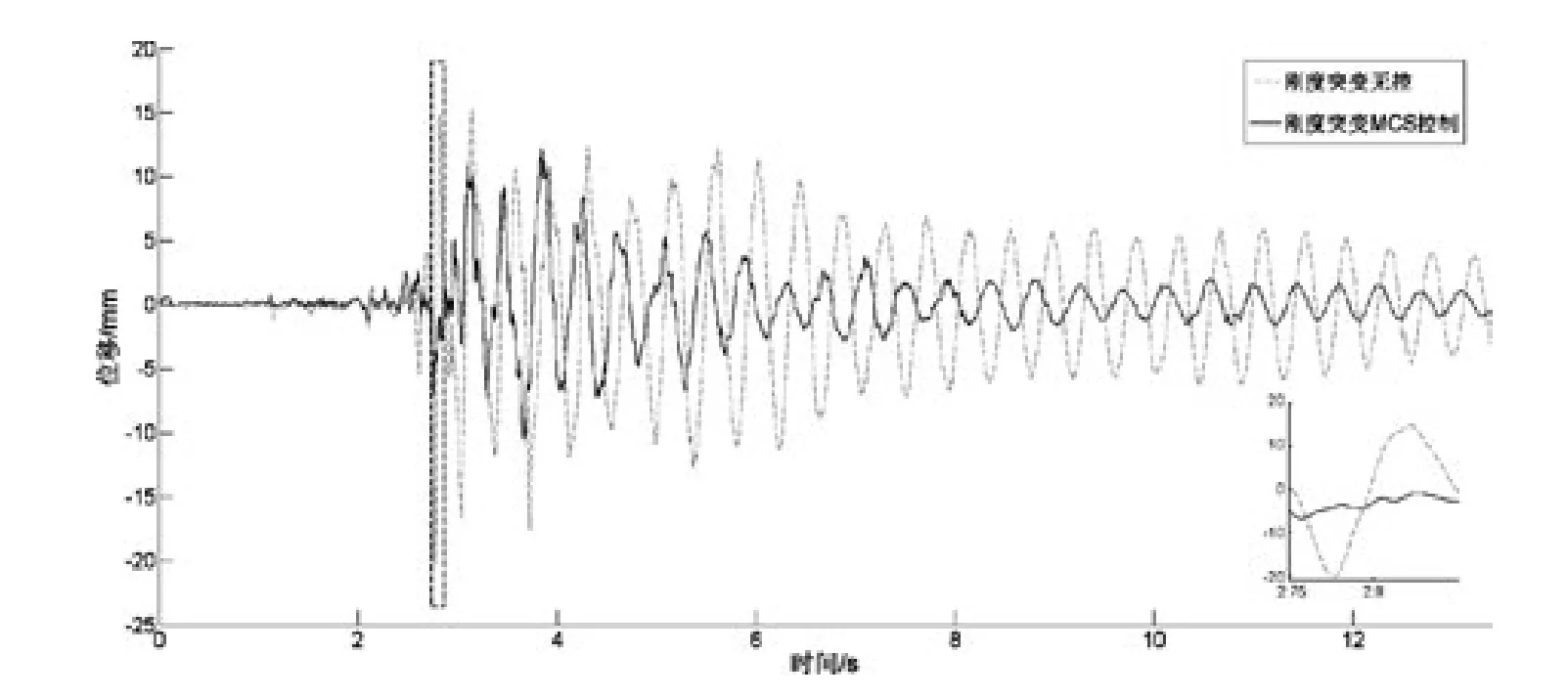
圖9 剛度突變情況下無控和采用MCS算法AMD控制的結構位移時程Fig.9 The displacement time history of structure controlled by AMD using MCSalgorithm or without control in the case of stiffness mutation

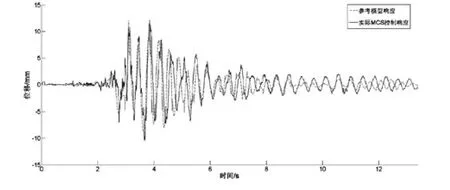
圖10 剛度突變情況下參考模型輸出位移與實際結構位移時程對比Fig.10 Comparison of time histories between output displacement of reference model and displacement of actual structure in the case of stiffness mutation

韓建平，呂西林，李慧.2007.基于性能的地震工程研究的新進展及對結構非線性分析的要求［J］.地震工程與工程振動，27(4):15-23.

盧圣治.2004.理論力學基本教程［M］.北京:北京師范大學出版社.

歐進萍.2003.結構振動控制［M］.北京:科學出版社.

彭凌云.2004.向心式摩擦阻尼器的理論分析及應用研究［D］.北京:北京工業大學.

秦榮.2006.工程結構非線性［M］.北京:科學出版社.

張凱靜，周莉萍，王官磊.2010.最小控制合成算法在結構振動控制中的應用［J］.華中科技大學學報，27(3):76-80.

Stoten D.P.，Beanchoubane H..1990a.Empirical studies of an MRAC algorithm with minimal controller synthesis［J］.International Journal of Control，51(4):823-849.

Stoten D.P.，Beanchoubane H..1990b.Robustness of a minimal controller synthesis Algorithm［J］.International Journal of Control，51(4):851～861.

Stoten D.P.，Gomez E.G..2001.Adaptive control of shaking tables using the minimal control synthesis algorithm［J］.The Royal Society，359:1697-1723.