自仿射接觸點及其在分形接觸理論中的應用

周安安,陳天寧,王小鵬,奚延輝

(西安交通大學機械工程學院,710049,西安)

?

自仿射接觸點及其在分形接觸理論中的應用

周安安,陳天寧,王小鵬,奚延輝

(西安交通大學機械工程學院,710049,西安)

為了深入研究分形方法在接觸理論中的應用,利用數值模擬實驗研究了分形粗糙表面的接觸機理,并提出了自仿射接觸點的概念。該概念充分利用分形函數自仿射的優點,改善了傳統分形接觸理論中微凸體不滿足分形特性的缺陷,去除了接觸理論中微凸體相互作用無法考慮等假設。將自仿射概念應用于分形接觸理論中,建立了新的接觸模型。模型基于粗糙表面均為各向同性的無潤滑表面且可以利用W-M函數模擬的假設,利用接觸中接觸點最大變形量與接觸面積的關系,對分形接觸模型進行修正,得到更符合實際情況的分形接觸理論。與經典的統計及分形接觸模型進行對比,結果表明:G-W模型是一個彈性模型,較少考慮塑性接觸,因此G-W模型在整體上會低估粗糙表面的接觸壓力;M-B模型利用單個余弦函數模擬微凸體,得到的最大接觸變形量偏小,且微凸體尺寸分布函數的使用也不準確,M-B模型高估了接觸壓力;提出的基于自仿射接觸點的分形接觸模型利用自仿射接觸點代替微凸體進行理論推導,能更準確地計算出接觸壓力;在相同的接觸面積下,粗糙表面分形維數越大或分形特征尺度越小,接觸壓力越小。

接觸理論;數值模擬;分形;微凸體

在過去的幾十年中,接觸機理的研究一直貫穿在各個領域中,如物理(包括機械、電、磁和熱等)、化學及生物研究等[1]。在此期間,很多學者提出了不同的接觸模型,文獻[2]創造性地將微凸體的高度分布與赫茲接觸理論結合,推導了整個粗糙表面上的彈性接觸模型(G-W模型)。此后,有很多學者基于G-W模型推導了一系列優化模型[3-5],但值得注意的是,G-W模型所使用的統計參數如表面粗糙度等對測量儀器的分辨率有很大的依賴性,所以不能對粗糙表面進行唯一表征,導致接觸模型也不唯一。因此,在證明了粗糙表面在一定尺度內滿足分形特性后[6-7],文獻[8]將分形理論引入接觸理論的研究中,推導了分形接觸理論(M-B模型)。M-B模型自從被提出后,就引起很多爭議,如很多學者意識到M-B模型中假設每個微凸體都完全變形是不正確的,因此文獻[9]改進了M-B模型,認為每個微凸體的變形量都可以是從0到最大變形量中的任意一個(M-E模型)。但是,M-E模型僅僅是單個微凸體的接觸模型,故文獻[10]利用M-E模型的方法推導了整個接觸表面上的接觸模型。本文研究發現M-B模型中還有一個嚴重的問題未被意識到:M-B模型利用著名的Weierstrass-Mandelbrot函數(W-M函數)模擬粗糙表面,并基于Hertz接觸理論推導接觸點上的壓力和接觸面積的關系,但卻僅僅用W-M函數中波長為l的余弦函數代表微凸體,該做法與分形的理念相違背。事實上,分形粗糙表面的任意接觸點都應該是自仿射的,即經過放大后,會有更多細節被觀察到。特別地,對于由W-M函數模擬生成的粗糙表面,每個接觸點都應該由多個余弦函數疊加而成。另外,在M-B模型中微凸體尺寸分布函數的使用也不準確。

因此,本文采用數值實驗的方法研究粗糙表面的接觸點,并提出一個新的、更加準確的接觸點的概念——自仿射接觸點,并將其應用到分形接觸理論中,推導出更符合分形定義的接觸理論。

1 數值模擬

本文的目的是通過數值仿真研究粗糙表面的分形特性,然后利用此特性修正分形接觸理論。首先采用多種不同的分形曲線驗證經典的Korcak經驗法則,然后進一步研究粗糙接觸表面上各個接觸點的接觸面積與該接觸點最大變形量的關系。

1.1 海島面積與個數的Korcak法則驗證

分形接觸理論的研究中廣泛地應用了文獻[11]中提出的Korcak經驗法則,即面積大于a的島嶼的個數服從以下規律

N(A>a)=Nca-B

(1)

式中:B為和島嶼輪廓有關的參數;Nc為比例系數。

Korcak經驗法則最早由地理學家Korcak在研究島嶼分布時提出,但限于當時的測試水平,只有3組島嶼被用做研究,而且關系式中的指數B被認為恒等于1/2。文獻[11]指出,參數B是一個和島嶼所在海岸線的輪廓有關的參數,B=Dc/2,Dc是海岸線的分形維數。如果轉化為適用于粗糙表面的關系式,則Dc=D-1,D為粗糙表面的分形維數。因此,對于二維粗糙表面B的范圍為[0,1/2],而對于三維表面,B的范圍為[1/2,1]。在M-B模型中,則認為B=D/2。從Korcak法則被提出以來,就不停有學者試圖驗證這種關系,文獻[7]試圖通過實驗的方法驗證Korcak法則,并用來預測粗糙表面微凸體的整體分布。盡管實驗確實證明了接觸點尺寸和個數符合指數關系,但并沒有證明指數B和分形維數D的關系。文獻[12]沒有通過驗證,而是直接利用Korcak法則計算粗糙表面的分形維數。至今為止,Korcak法則盡管被多次使用,但尚未被人明確證明是否普遍適用于任何分形表面,或者是否適用于粗糙表面上微凸體尺寸分布的研究。因此,本文將通過大量的數值實驗驗證Korcak法則及其在粗糙表面研究中的適用性。

1.1.1 模擬分形表面的點數對模擬結果的影響 本文選用分形維數D=1.2的粗糙表面測試數值模擬結果,模擬點數獨立性如圖1所示。之所以要做模擬點數獨立性測試,是因為當模擬點數達不到一定數量時,分形表面就不會表現出自仿射性。換言之,當利用電腦軟件模擬一個確定輪廓時,如果使用的點數不夠,也就是分辨率太低的話,經過多次放大后的輪廓,不會跟原來的相似。因此,在對Korcak法則進行驗證之前,有必要先研究用于分形表面模擬的點數對模擬結果的影響。

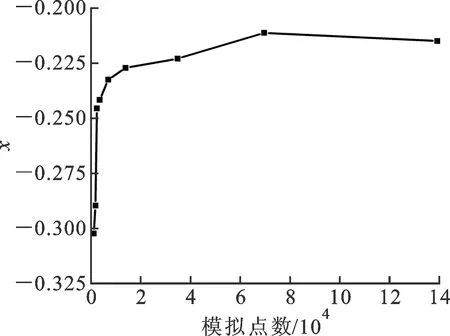
圖1 模擬點數對結果的影響

由圖1發現,隨著模擬點數的增加,模擬結果逐漸趨于穩定,當點數超過70 000后,數值模擬結果基本可以認為跟模擬點數的選取無關。因此,本文選取最優化點數為70 000來模擬粗糙表面輪廓,圖1中的縱坐標指數x將會在后面進一步討論。

1.1.2 Korcak海島實驗數值仿真 本文利用數值仿真的方法驗證Korcak測試海島分布的實驗。首先,用經典的W-M函數生成海底輪廓,而海平面則用一個絕對平面代替,如圖2所示。從圖2可以看到,復雜的海底輪廓被海平面截斷,而截斷的面積就是海島的面積。

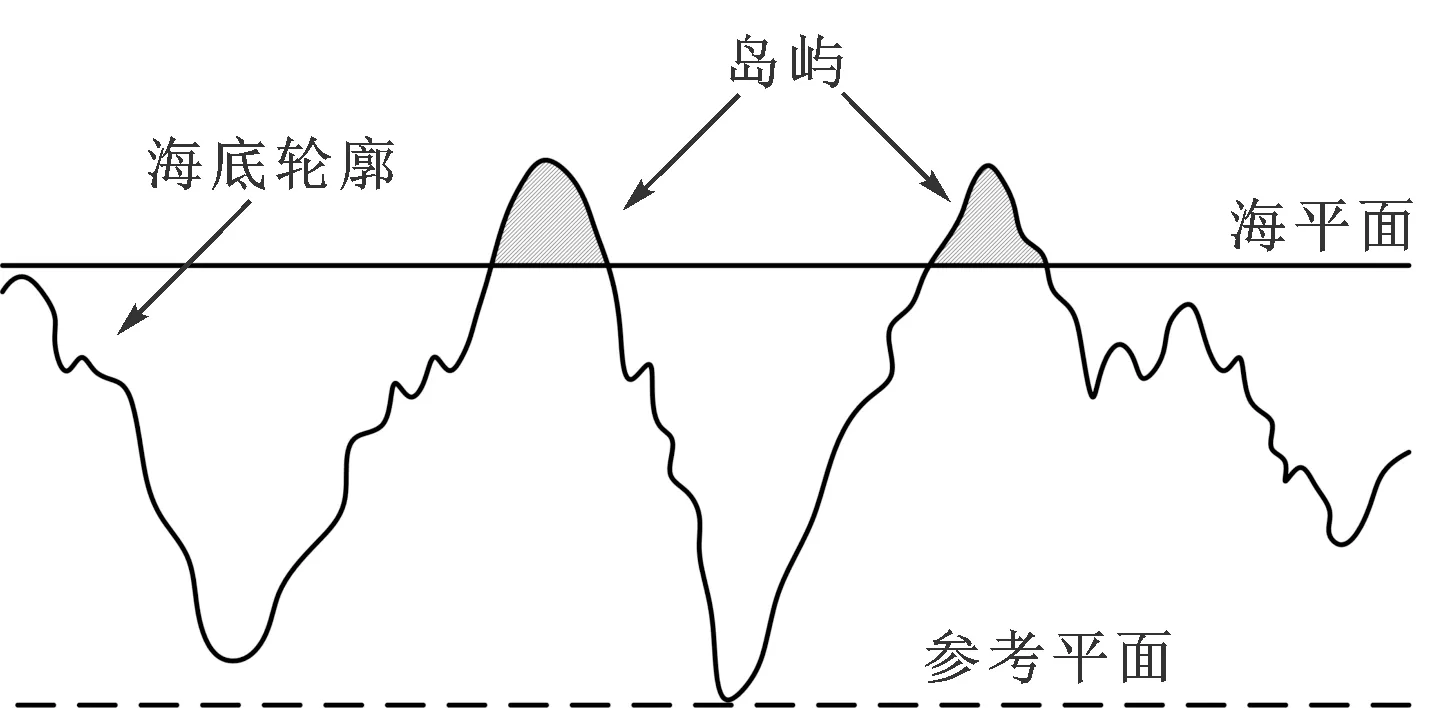
圖2 Korcak實驗示意圖

如同Korcak在實驗中所做的,本文利用軟件對一定取樣長度內的島嶼個數N及島嶼直徑l進行了記錄,即所有被海平面截斷的海底輪廓的長度和個數,結果表明:大于某一確定直徑的島嶼的個數隨此直徑的增大而減小,其在雙對數坐標下的關系如圖3所示。

圖3 島嶼個數N與島嶼直徑l的關系

從圖3可以看出,島嶼個數N與島嶼直徑l滿足指數關系,即

N(L>l)=Ncllx

(2)

式中:Ncl為比例系數。

為了研究指數x與海底輪廓的分形維數D的關系,本文分別選取從1.2到1.8的7組不同分形維數的海底輪廓進行Korcak海島實驗,從而得到了指數x和分形維數D的關系如圖4所示。從圖4中可以看出,指數x和分形維數D的關系可表示為

x=1-D

(3)

因此式(2)可化為

N(L>l)=Ncll1-D

(4)

為了驗證式(4)并非某種特定曲線的特例,除了W-M函數外,本文還選用分形布朗函數模擬分形表面(海洋輪廓),得到的結果如圖4所示。兩種曲線得到的結果基本無差別,從而證明式(4)所示的關系是所有分形表面的固有特性。至此,Korcak的海島實驗已經通過軟件模擬的方法得到了驗證。因為Korcak法則是分形曲線的固有特性,所以在驗證過程中,如果將海底輪廓改為粗糙表面,亦可證明,Korcak法則同樣適用于分形粗糙表面。

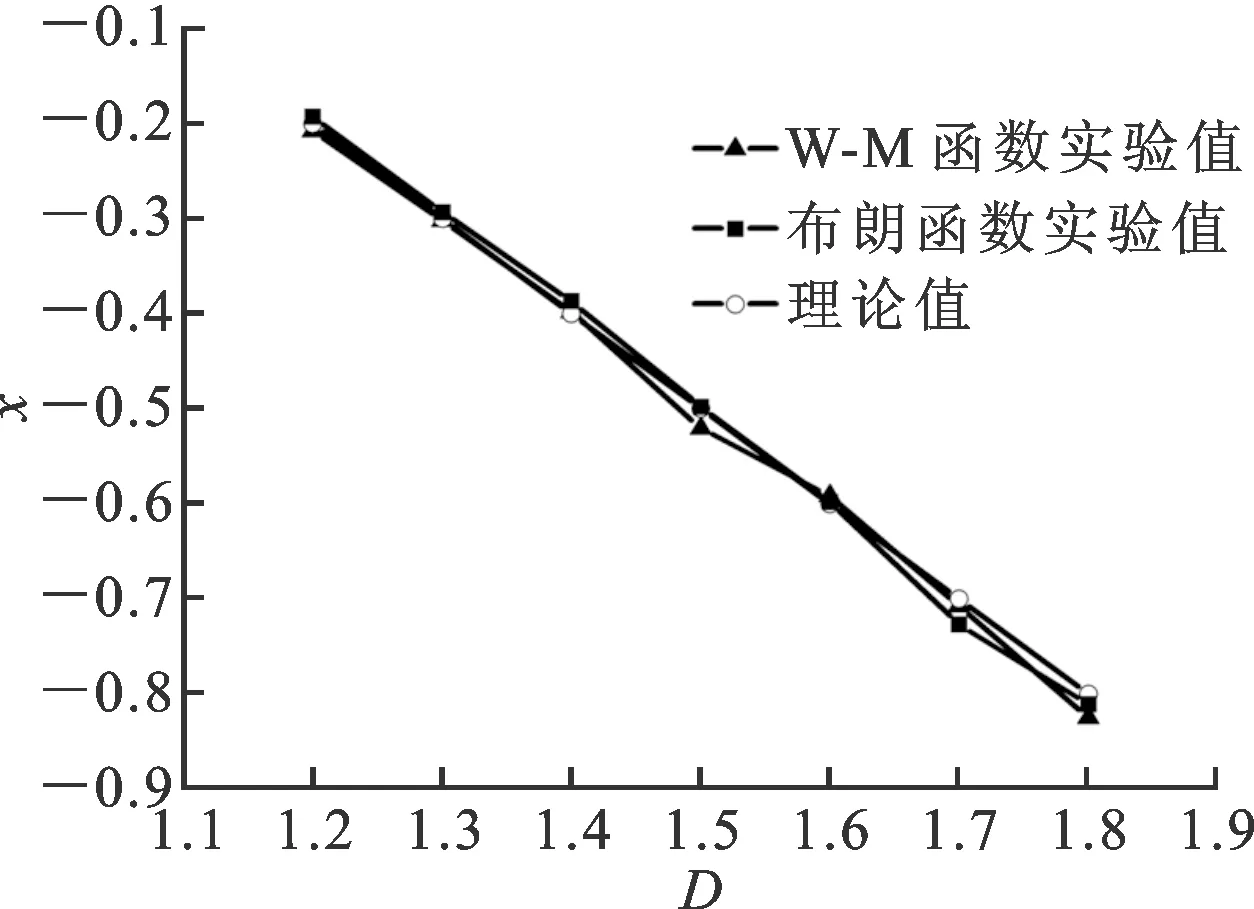
圖4 指數x和分形維數D的關系

1.1.3 不同的海平面高度對實驗結果的影響 現實中,海平面處于不停的波動狀態,每次測量時,海平面高度都是隨機的,因此本文做了一個有趣的數值實驗以研究不同海平面高度對實驗結果的影響,結果如圖5所示。圖中選取的海底輪廓的分形維數為1.3,對于每個海平面高度,本文都分別進行了3次Korcak海島實驗。通過圖5可以觀察到,海平面的輕微波動不會影響實驗結果,但當海平面過高或過低(高于海島輪廓高度的80%或低于海底輪廓高度的30%)時,實驗結果可能出現較大誤差。這在證明Korcak經驗法則的穩定性的同時,也從另一方面證明,Korcak在不同時間內測得的島嶼個數與島嶼面積的關系無太大的差別。

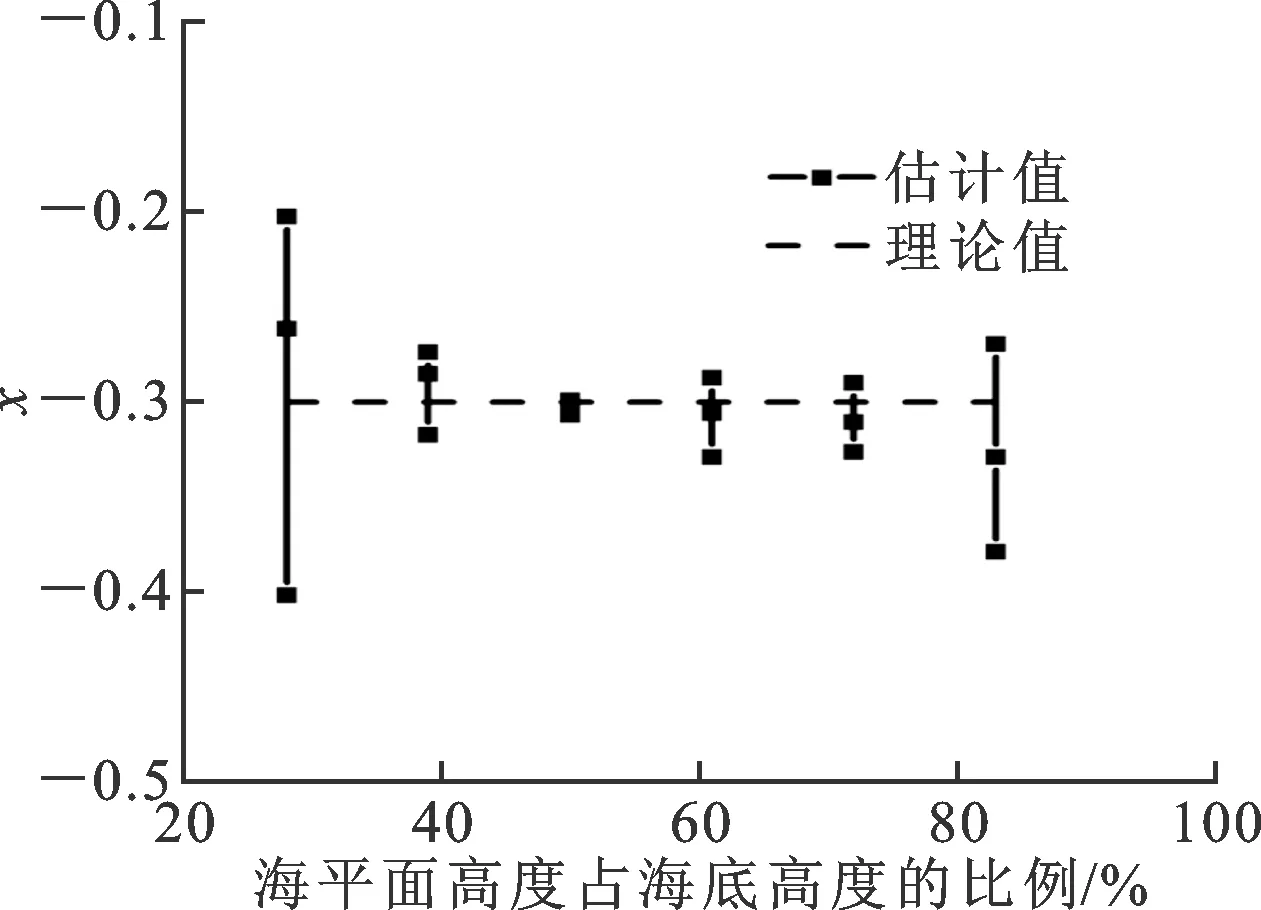
圖5 不同海平面高度占海底高度的比例對實驗結果的影響

1.2 接觸點面積與該接觸點上最大變形量的關系

看上去近乎平面的粗糙表面上其實有很多大小不一的微凸體[13-14]。當兩粗糙表面接觸時,隨著接觸壓力的增加,粗糙表面上接觸到的微凸體會逐漸消失或者結合成為更大的微凸體,所以對微凸體的跟蹤較為復雜。不同于M-B模型,本文將不再研究微凸體如何變形,而僅討論自仿射接觸點(簡稱接觸點)的變化。接觸點和微凸體的區別在于接觸點是一個動態概念,在接觸過程中存在,離開接觸便沒有意義,并且一個接觸點可能由很多微凸體組合而成。因此,接觸點的概念比微凸體更復雜而且更適合用于研究接觸過程。利用W-M函數生成的粗糙表面上的接觸點也應該是很多余弦函數疊加的結果,因為W-M函數本身就是多個余弦函數的疊加,而在M-B模型中,卻利用單余弦函數模擬微凸體,這必然導致計算結果不準確。另外,使用接觸點的概念也可以排除分形接觸模型中的很多假設,如傳統接觸理論中,認為微凸體之間的相互作用可以忽略,這和實際不太相符。利用接觸點的概念后,將不再需要考慮微凸體的相互作用,因為接觸點本身就是微凸體相互作用的結果,如果沒有相互作用,微凸體和接觸點的概念將是一致的。然而,多余弦函數疊加的顯示表達式并不容易獲得,所以從M-B模型被提出到現在,都沒有學者提出改進方案。鑒于以上原因,本文利用數值仿真實驗方法,統計地研究接觸點最大變形量與接觸面積的關系,然后利用此關系對分形接觸模型進行修正,得到更符合實際情況的分形接觸理論。

粗糙表面間的接觸可簡化如圖6所示。首先,利用W-M函數生成一個可變形的分形粗糙表面,然后使剛性平面與該粗糙表面接觸,得到截斷后的表面。在這個過程中,本文記錄了接觸點直徑l與最大接觸變形量zmax關系如圖7a所示,對圖中的點進行擬合并畫在雙對數坐標下如圖7b所示,其中分形特征尺度G=0.12 m1/2,分形維數D=1.7。

圖6 兩粗糙表面接觸的簡化示意圖

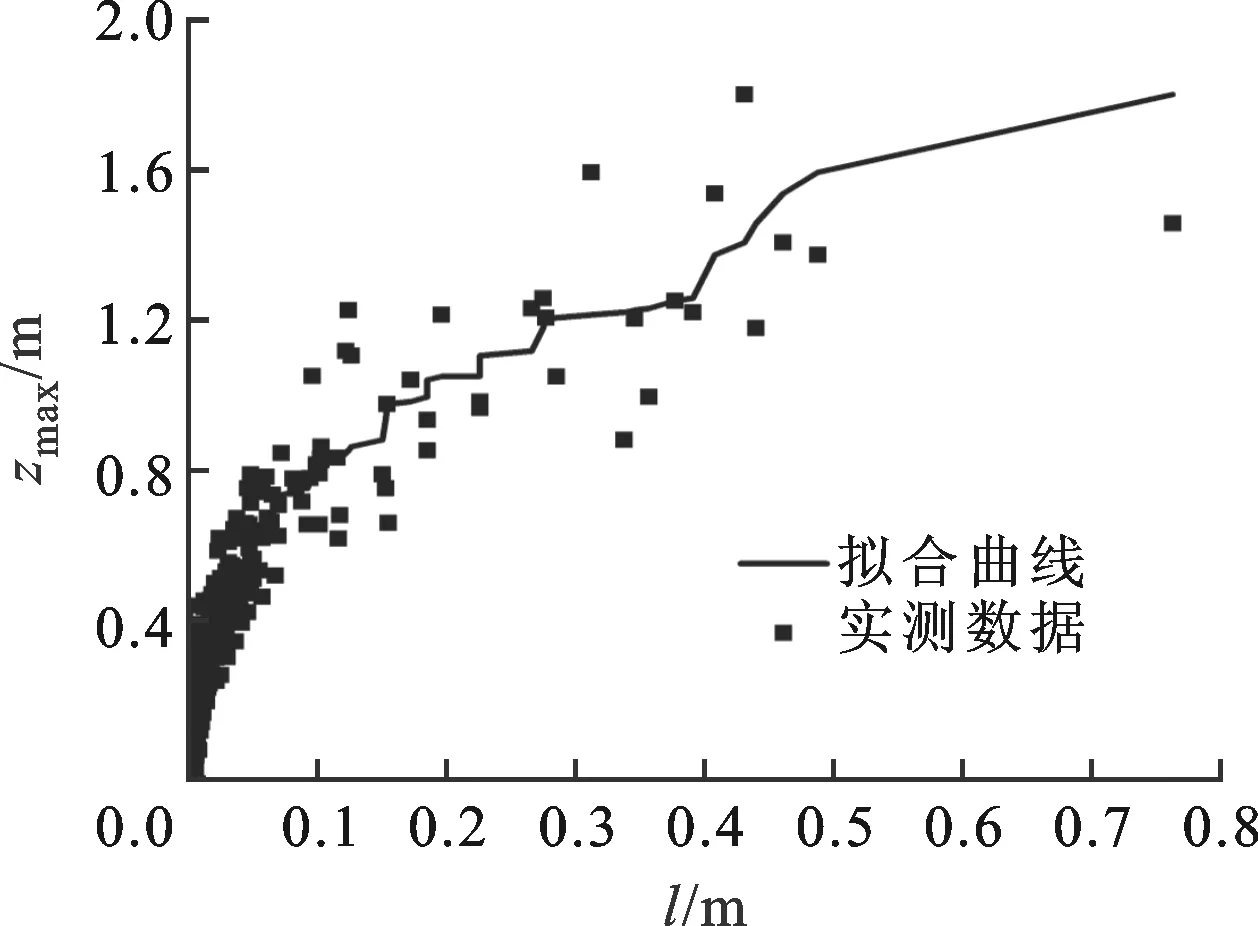
(a)接觸點直徑l與最大變形量zmax的關系

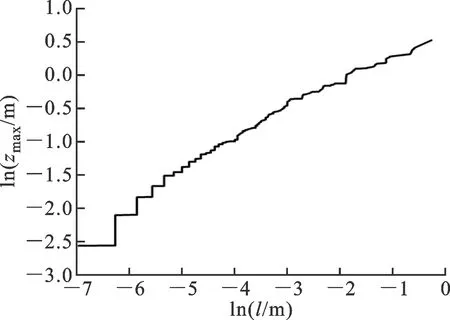
(b)接觸點直徑l與最大變形量zmax關系的雙對數形式圖7 最大變形量與接觸點直徑的關系

通過圖7可以發現,在雙對數坐標下接觸點直徑和最大變形量近似滿足線性關系,因此最大變形量可以假設為

zmax=Imlxm

(5)

式中:Im和xm分別為最大變形量時的乘子和指數。值得注意的是,在傳統的M-B模型中,zmax-MB=GD-1l2-D,G被定義為粗糙表面的分形特征尺度,但這僅僅是利用單余弦函數模擬微凸體而得到的結果。

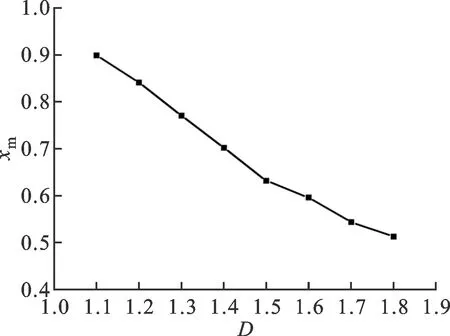
圖8 指數xm和分形維數D的關系

1.2.1 指數xm本文通過W-M函數模擬了不同的分形曲線,從而得到了指數xm和分形維數D的關系如圖8所示。圖8表明,指數xm和分形維數D近似滿足線性關系,即

(6)

對于M-B模型中的微凸體,xm-MB=2-D。本文同樣對不同的分形特征尺度G進行了研究,同時除了W-M函數外,分形布朗函數也被用作模擬粗糙表面輪廓。研究發現,指數xm由分形維數D唯一決定,跟其他參數無關。

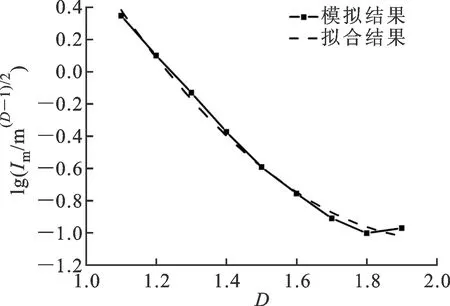
1.2.2 乘子Im比起指數xm,乘子Im的確定更復雜。在不同的分形特征尺度下,乘子隨分形維數的變化情況也不同,如圖9所示。從圖9中可以總結以下兩點。

(a)G=1.2×10-3 m1/2

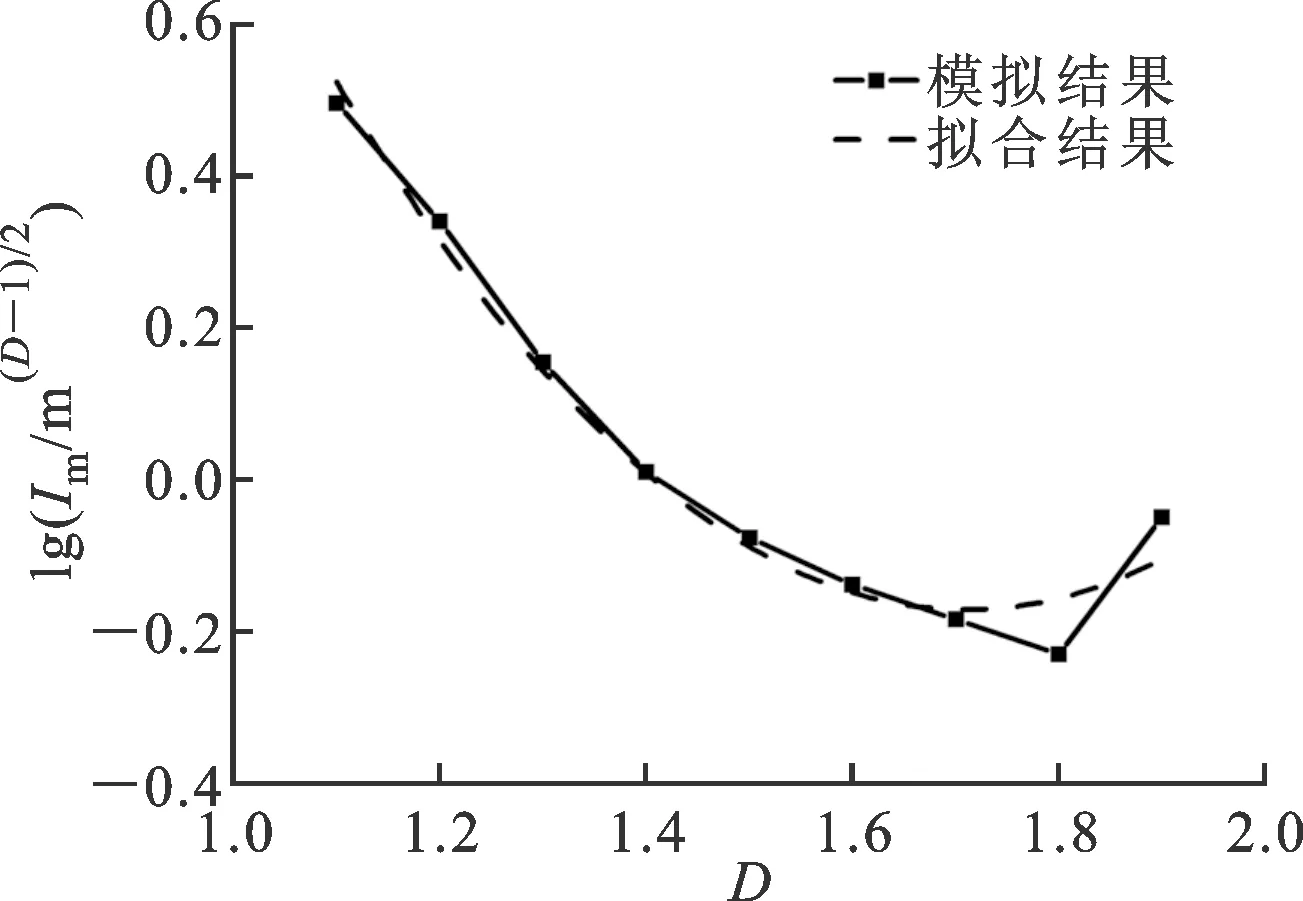
(b)G=1.2×10-2 m1/2

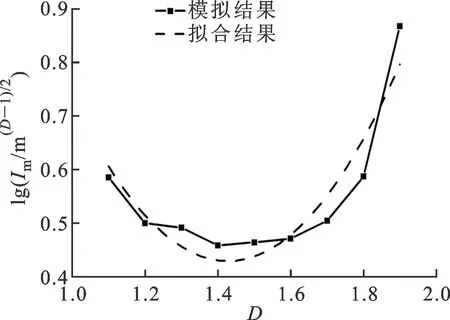
(c)G=1.2×10-1 m1/2

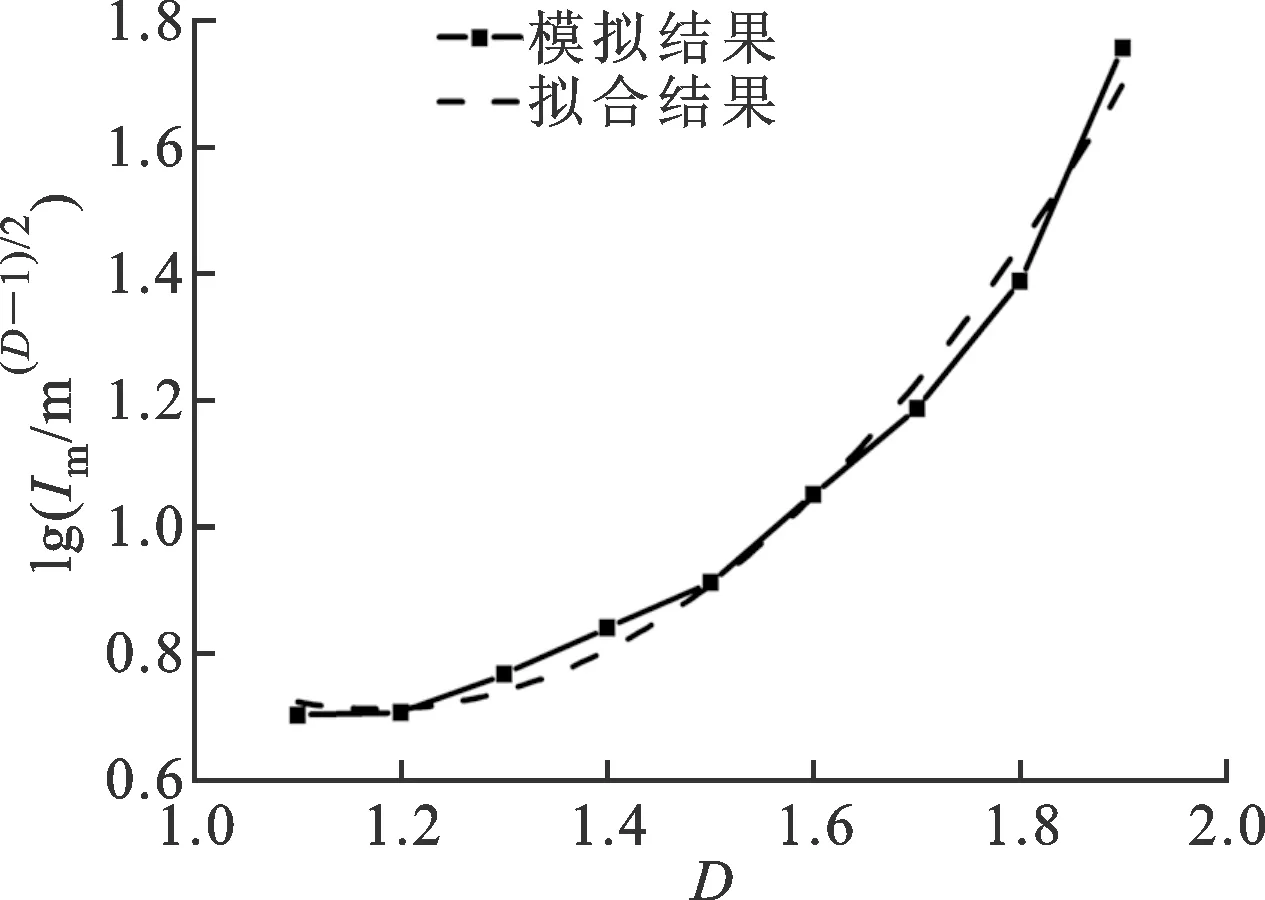
(d)G=1.2 m1/2圖9 不同分形特征尺度G下乘子與分形維數的關系

(1)乘子Im由分形特征尺度G和分形維數D共同決定。在不同的特征尺度G下,乘子隨分形維數的變化規律也不同,圖9中利用多項式擬合了這一關系。

(2)隨著分形特征尺度G的增加,最小乘子所對應的分形維數逐漸減小。

本文利用多項式擬合乘子與分形維數及特征尺度的關系

lgIm=3-lgG+(-4+lgG)D+1.8D2

(7)

Im=GD-1101.8D2-4D+3

(8)

而對于M-B模型,Im-MB=GD-1,兩者之比為

(9)

從式(9)可以發現,隨著分形維數的增加,兩種方法得到的最大變形量的比值也逐漸增加,當分形維數D=1.1時,比值最小。換言之,分形維數越大,多余弦函數疊加的效果也就越顯著。

為了對比單余弦函數和多余弦函數構造接觸點的不同,本文選取參數G=0.12 m1/2、D=1.5來構造接觸點,通過圖10可以發現,單余弦函數所構造接觸點的最大變形量過小。

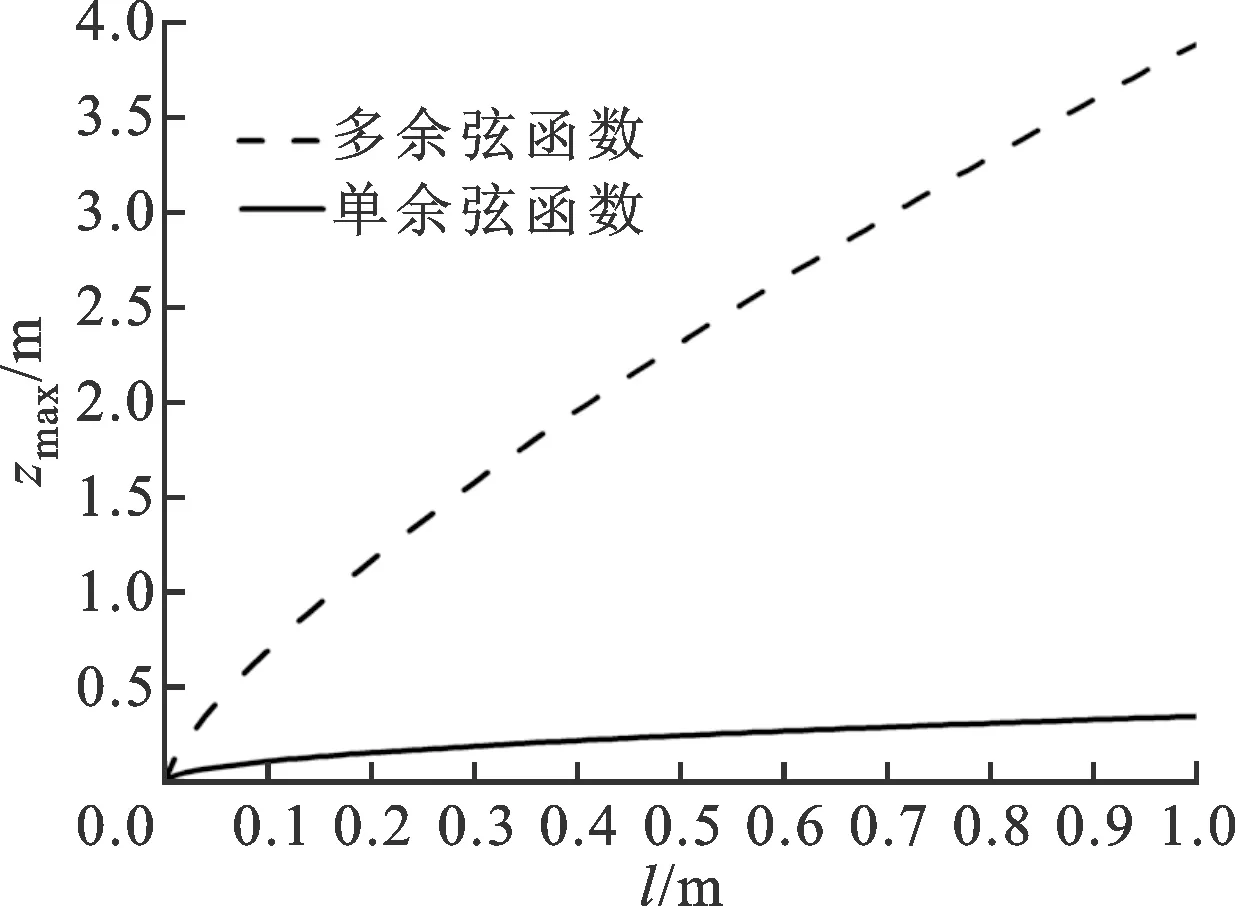
圖10 單余弦函數和多余弦函數構造接觸點的對比

2 基于自仿射接觸點的分形接觸模型

在得到自仿射接觸點的最大變形量與接觸面積的關系后,本文將利用此關系進一步推導新的分形接觸模型。本文推導的分形接觸模型基于粗糙表面均為各向同性的無潤滑表面,并且可以利用W-M函數模擬的假設。如圖6所示,由于所有接觸都不完美,接觸表面由很多個不同尺度的接觸點組成。在經典分形接觸模型M-B中,微凸體概念的使用并不準確,因此在對其進行改正,得到一個全新的、更加準確的接觸點定義后,本文將推導更符合粗糙表面分形特性的分形接觸理論。

在利用W-M函數生成的分形表面上,接觸點表現為由多個余弦函數疊加而成,如圖11所示。

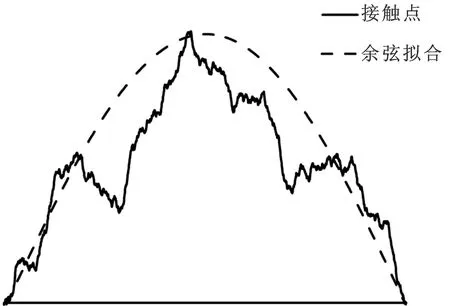
圖11 分形粗糙表面接觸點示意圖

從圖11中可以看出,單一接觸點的形狀與余弦函數很相似。因此,在得到接觸點最大變形量與接觸直徑的關系后,本文假設直徑為l的接觸點的變形量可表示為

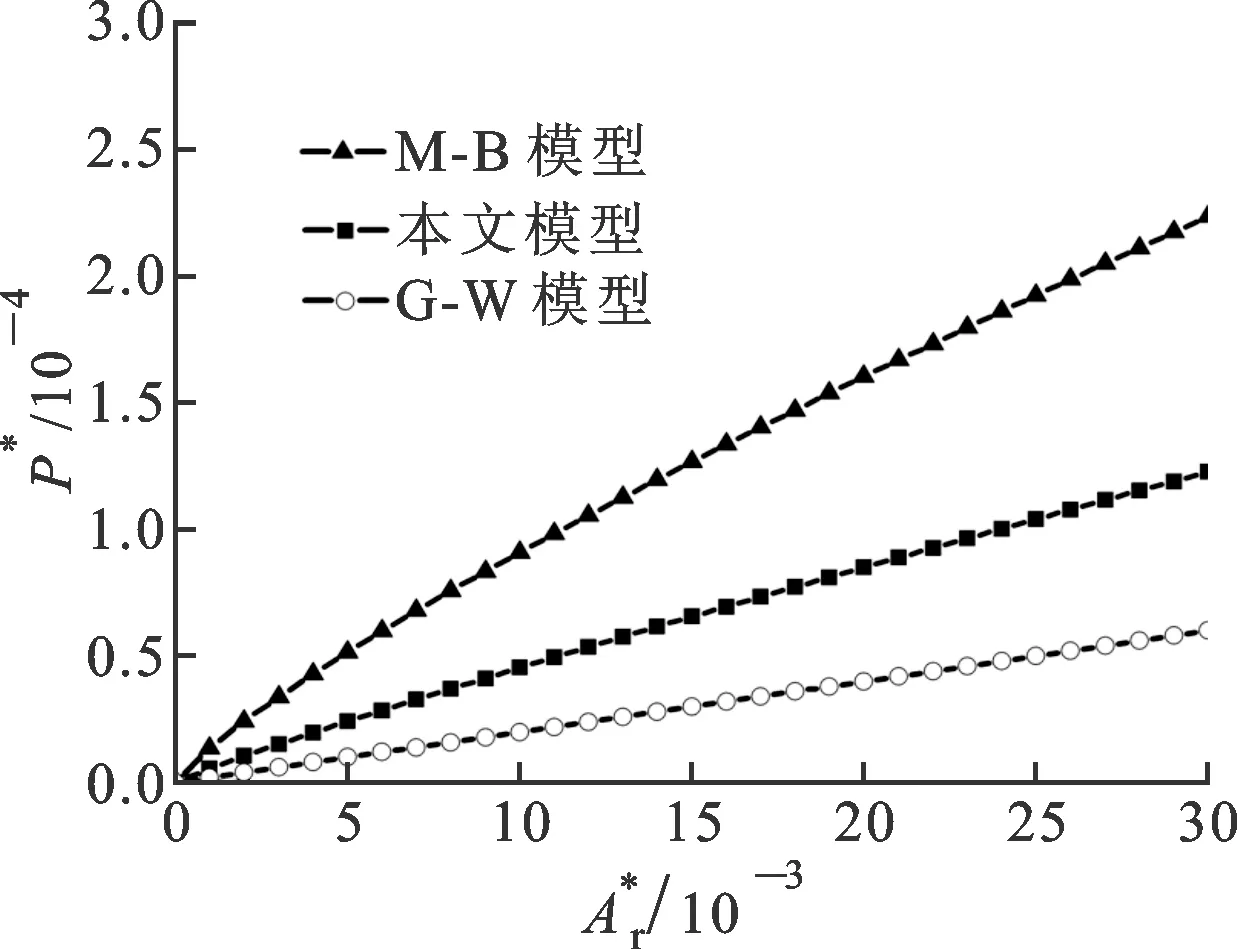
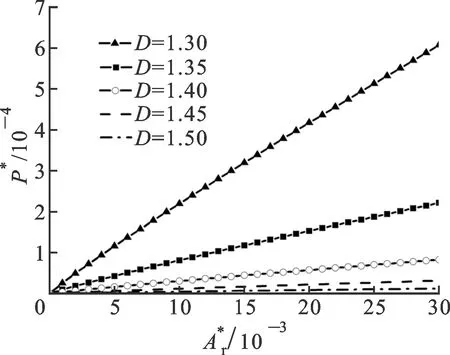
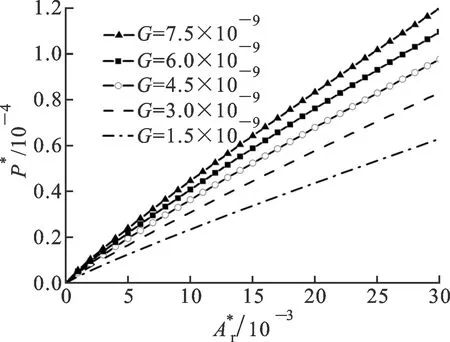
-l/2

(10)

該接觸點在頂點處的曲率半徑為[2]

(11)

在第1節中已經證明經典的Korcak法則適用于粗糙接觸表面,即

(12)

式中:al為接觸點最大接觸面積。因此,接觸點的尺寸分布函數可由式(12)的微分得到

(13)

根據Hertz接觸理論,接觸點的接觸面積和彈性接觸壓力可表示為

a=πRz

(14)

(15)

式中:E為復合彈性模量。

塑性接觸壓力為[8]

pp(a)=Kσya

(16)

式中:K為材料硬度系數;σy為材料屈服強度。

將式(14)和式(11)帶入式(15),得到彈性接觸壓力和接觸面積的關系為

(17)

由于受力的不同,粗糙表面的接觸點將表現為彈性變形或塑性變形的狀態,而彈性變形與塑性變形的臨界變形量為[2]

(18)

利用本文得到的接觸點的最大變形量與接觸面積的關系,可得接觸點的臨界接觸面積為

(19)

式中:φ=σy/E。

正如傳統分形接觸理論M-B模型中發現的一樣,本文接觸點的變形規律同樣為:當接觸點的接觸面積大于臨界接觸面積時,接觸點處于彈性接觸階段;當接觸面積小于臨界接觸面積時,接觸點處于塑性接觸階段。這一特點與傳統的認識相悖,也有學者一直在爭論稱其不合理,因此本文將結合分形表面的特點論述這一規律。

對于分形表面上任意一個接觸點,不論接觸面積大小,其最大接觸變形量與接觸直徑滿足式(5),因此最大接觸變形量與接觸直徑的比值為ζ=zmax/l=Iml(1-D)/2。由于分形維數1

將式(13)帶入單個接觸點的接觸壓力表達式,即可得到整個接觸面上的彈性和塑性接觸壓力

對于不同材料及尺寸的粗糙表面,將總壓力轉換為非量綱形式將更有利于對比研究

3 模型對比結果與討論

3.1 與M-B模型及G-W模型對比

為了驗證推導得到的接觸模型,將本文模型與經典的M-B和G-W模型進行對比,如圖12所示。其中比較關心的參數有D=1.38,G*=10-10,Aa=10-6m2及φ=0.05[8]。

圖12 3種模型結果對比

通過圖12可以看出,由于G-W模型是一個彈性模型,較少考慮塑性接觸,因此G-W模型在整體上會低估粗糙表面的接觸壓力,M-B模型則利用W-M函數中的單個余弦函數模擬微凸體。本文的研究表明,自仿射接觸點比微凸體更適合應用于分形接觸模型的推導中,在接觸中,單個余弦函數模擬微凸體所得到的最大接觸變形量偏小。另外,M-B模型中微凸體尺寸分布函數的使用也不準確。綜上所述,M-B模型高估了接觸壓力。因此,圖12說明本文推導的模型能更加準確地揭示接觸機理。

3.2 分形維數及分形特征尺度對結果的影響

在分形接觸模型中,粗糙表面的分形維數和特征尺度由接觸表面的材料決定,因此有必要研究分形維數及特征尺度對分形模型模擬結果的影響。本文選取了不同的分形維數對比理論推導,結果如圖13所示。在相同的接觸面積下,分形維數越大的表面,接觸壓力越小。究其原因,分形維數和接觸點的分布有直接關系:在一定的面積內,接觸點越多,粗糙面的分形維數越大。因此,分形維數越小的表面,就需要越大的力以使粗糙表面發生相同的變形,從而具有相同的接觸面積。

圖13 分形維數對接觸模型的影響

本文選取不同的分形特征尺度對比理論推導,結果如圖14所示。結果與預想的一樣,為了達到相同的接觸面積,具有較大分形特征尺度的表面需要的變形量更大,因此壓力也必須足夠大。

圖14 分形特征尺度對接觸模型的影響

4 結 論

(1)利用數值實驗方法,通過選用不同的分形曲線驗證了分形研究中廣泛使用的Korcak法則,同時研究了不同的海岸線高度對實驗結果的影響,從而證明Korcak法則是分形曲線的固有特性。

(2)研究了分形粗糙表面的接觸機理,發現在傳統的分形接觸理論中,微凸體概念的使用并不恰當,因此利用自仿射接觸點代替微凸體進行理論推導。

(3)得到了接觸點變形量和接觸點面積的關系。隨后,利用赫茲接觸理論,計算了產生該變形量所需的接觸壓力,結合接觸點的尺寸分布函數得到了整個粗糙表面的壓力分布,從而推導了新的接觸模型。研究表明,不同的分形維數和分形特征尺度對接觸模型的影響較大。

[1]GORYACHEVA I G.Contact mechanics in tribology [M].Berlin, Germany: Springer-Verlag, 1998: 1-3.

[2]GREENWOOD J A, WILLIAMSON J B P.Contact of nominally flat surfaces [J].Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319.

[3]CHANG W R, ETSION I, BOGY D B.An elastic-plastic model for the contact of rough surfaces [J].Journal of Tribology, 1987, 109(2): 257-263.

[4]ZHAO Y W, MAIETTA D M, CHANG L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow [J].Journal of Tribology, 2000, 122(1): 86-93.

[5]YOU J M, CHEN T N.Statistical model for normal and tangential contact parameters of rough surfaces [J].Proceedings of the Institution of Mechanical Engineers: Part C Journal of Mechanical Engineering Science, 2011, 225(1): 171-185.

[6]MAJUMDAR A.Fractal surfaces and their applications to surface phenomena [D].Berkeley, USA: University of California, 1989.

[7]MAJUMDAR A, BHUSHAN B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J].Journal of Tribology, 1990, 112(2): 205-216.

[8]MAJUMDAR A, BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces [J].Journal of Tribology, 1991, 113(1): 1-11.

[9]MORAG Y, ETSION I.Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces [J].Wear, 2007, 262(5): 624-629.

[10]MIAO X M, HUANG X D.A complete contact model of a fractal rough surface [J].Wear, 2014, 309(1): 146-151.

[11]MANDELBROT B B.The fractal geometry of nature [M].London, UK: MacMillan, 1983: 116-119.

[12]RUSS J.Fractal surfaces [M].New York, USA: Springer-Verlag, 1994: 14-16.

[13]張學良, 黃玉美.機械結合部動態特性參數識別的優化方法 [J].太原重型機械學院學報, 1995, 16(4): 314-318.

ZHANG Xueliang, HUANG Yumei.An optimization method for identification of machine joint structural parameters [J].Journal of Taiyuan Heavy Machinery Institute, 1995, 16(4): 314-318.

[14]尤晉閩, 陳天寧.結合面法向動態參數的分形模型 [J].西安交通大學學報, 2009, 43(9): 91-94.

YOU Jinmin, CHEN Tianning.Fractal model for normal dynamic parameters of joint surfaces [J].Journal of Xi’an Jiaotong University, 2009, 43(9): 91-94.

[本刊相關文獻鏈接]

方江龍,王小鵬,陳天寧,等.動理論在預測非阻塞性顆粒阻尼能量耗散中的應用.2015,49(4):12-17.[doi:10.7652/xjtuxb201504003]

田紅亮,趙美云,鄭金華,等.新的柔性結合部法向接觸剛度和接觸阻尼方程.2015,49(1):118-126.[doi:10.7652/xjtuxb201501020]

田紅亮,陳從平,方子帆,等.應用改進分形幾何理論的結合部切向剛度模型.2014,48(7):46-52.[doi:10.7652/xjtuxb 201407009]

李昕,張娟,李全福,等.面向集成電路的大尺寸單晶石墨烯的可控制備方法.2014,48(6):103-109.[doi:10.7652/xjtuxb201406018]

張超,陳天寧,王小鵬,等.顆粒阻尼線性離散元模型參數的選取方法.2014,48(3):96-101.[doi:10.7652/xjtuxb201403 018]

舒歌群,趙文龍,梁興雨,等.約束阻尼結構的振動分析及結構參數優化研究.2014,48(3):108-114.[doi:10.7652/xjtuxb201403020]

歐陽武,陳潤霖,彭林,等.考慮局部固體接觸的滑動軸承主剛度和主阻尼研究[J].2014,48(1):112-117.[doi:10.7652/xjtuxb201401019]

劉石,仲繼澤,馮永新,等.使用磁流變阻尼器的大型汽輪發電機定子端部繞組振動控制.2013,47(4):39-43.[doi:10.7652/xjtuxb201304008]

宿月文,陳渭,朱愛斌,等.分形特征表面接觸磨損模擬.2013,47(7):52-56.[doi:10.7652/xjtuxb201307010]

薛士明,曹軍義,林京,等.分數階阻尼裂紋轉子的非線性動力學特性分析.2012,46(1):76-80.[doi:10.7652/xjtuxb 201201014]

田紅亮,趙春華,朱大林,等.整個螺栓結合部的法向連接動剛度及試驗驗證.2012,46(9):31-36.[doi:10.7652/xjtuxb 201209007]

張學良,溫淑花,蘭國生,等.平面結合面切向接觸阻尼分形模型及其仿真.2011,45(5):74-77.[doi:10.7652/xjtuxb 201105014]

王建偉,徐暉,馬寧.內嵌自主移動鋼球歐拉梁自適應碰撞減振研究.2010,44(11):103-108.[doi:10.7652/xjtuxb201011 021]

劉雅琳,徐自力,上官博,等.時頻域交互法在微滑移干摩擦阻尼葉片振動分析中的應用.2009,43(11):22-26.[doi:10.7652/xjtuxb200911005]

尤晉閩,陳天寧.結合面法向動態參數的分形模型.2009,43(9):91-94.[doi:10.7652/xjtuxb200909020]

曹軍義,謝航,蔣莊德.分數階阻尼Duffing系統的非線性動力學特性.2009,43(3):50-54.[doi:10.7652/xjtuxb200903 011]

(編輯 杜秀杰)

Self-Affine Contact Spot with Applications in Fractal Contact Theory

ZHOU An’an, CHEN Tianning, WANG Xiaopeng, XI Yanhui

(School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The numerical simulation for contact essence between fractal rough surfaces is conducted, and a concept of self-affine contact spot is introduced to propose a new fractal contact model.Compared with the asperity in classical fractal contact model, the self-affine contact spot better describes the process of fractal contact.The self-affine contact spot now gets fractal, and the assumption of no interaction between asperities is unnecessary.Under the assumption that the rough surfaces are all unlubricated isotropic surfaces, this model can be simulated by W-M function.Making use of the relationship between the maximum deformation and contact area of contact spot, the classical fractal contact model is modified to further approach the engineering practice.It is found that G-W model ignores plastic deformation of contact spot thus to underestimate the contact load of rough surfaces; M-B model leads to a smaller maximum deformation to difficultly use size-distribution function and overestimates the contact load.The self-affine contact spot instead of asperity enables to accurately evaluate the contact pressure, The more the fractal dimension (or the less the fractal characteristic scale), the less the contact pressure is needed for same contact area.

contact theory; numerical simulation; fractal; asperity

2014-09-28。 作者簡介:周安安(1987—),男,博士生;陳天寧(通信作者),男,教授,博士生導師。 基金項目:國家科技重大專項資金資助項目(2011ZX04002-031);陜西省科學技術研究發展計劃資助項目(2014SJ-09)。

時間:2015-03-23

http:∥www.cnki.net/kcms/detail/61.1069.T.20150323.1713.004.html

10.7652/xjtuxb201506002

TH113.1

A

0253-987X(2015)06-0008-08