基于邊界元法聲場輻射預測研究
呂國策
長春職業技術學院,吉林長春 130000
基于邊界元法聲場輻射預測研究
呂國策
長春職業技術學院,吉林長春 130000
采用邊界元法預測結構振動的聲場聲壓,已經得到廣泛研究,然而邊界積分方程建立的過程中遇到奇異積分,雖然此時也采用高斯積分,但計算收斂性降低。本文針對奇異積分問題采取廣義極坐標變換,對比了兩種結構網格對邊界元法計算結果的影響,結果表明,采用廣義極坐標變換后,邊界元法可以預測振動輻射聲場聲壓,當頻率升高時,某些頻率結果誤差增加,為此,在提高網格質量后,在低頻情況兩種結果與解析解極為接近,高頻段較好的網格質量度數值計算結果的精度有所提高,但計算時間乘倍增加,不利于工程實際,對于大型問題要綜合考慮,在不影響計算精度的同時,可以適當降低網格數量,以降低計算時間。
邊界元;奇異積分;廣義極坐標變換
由于機械振動產生強烈的噪聲,工程中振動產生的噪聲越來越受到人們的關注,而噪聲對現場工作人員產生極大心理和勝利危害,為解決此問題,各國都相應出臺了相應的措施限制現場噪聲,機械制造商相應的也對其產生的噪聲采取了相應的控制措施。對生產制造商而言,在進行制造前提前預知機械產生的噪聲強度對后續工作有指導意義,所以需要一種有效地計算輻射聲場聲壓方法[1-3]。
1 邊界元方程的建立
聲在介質中傳播,假設介質為理想流體,流體不存在粘滯性,沒有擾動,宏觀上靜止,且介質絕熱,并且聲波是小振幅聲波,聲壓遠小于介質靜態聲壓,由以上假設可以將非線性問題轉化為線性聲輻射問題,而我們關注的多數問題都是脈動振源產生的穩定的簡諧聲波,所以有聲壓輻射公式[4-5]

根據理想流體小振幅聲波輻射的波動方程,可以得到helmholtz等式。

其中k為波數, /k cω= ,其伴隨方程為

伴隨方程的基本解為

我們僅考慮輻射聲壓,所以有B=0,有伴隨方程的基本解

利用第二格林公式建立邊界積分方程
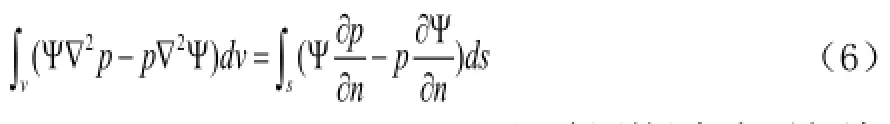
假設基本解和聲壓滿足此方程,得到場點聲壓與邊界信息之間的關系
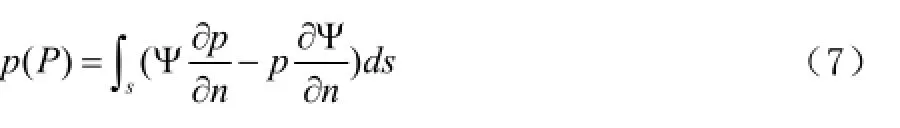
2 邊界奇異積分的處理
對于給定的結構,可能僅了解邊界表面振動部分信息,然而通過以上邊界積分方程可知,要得到場點聲壓,必須要有所有邊界信息,包括表面振動速度和聲壓,當給定邊界條件時,可以將場點p配置到邊界表面上,然而基本解這時存在奇異性,對于奇異積分的處理,本文采用極坐標變換法引進雅克比消除奇異積分的方法。
如圖1所示,將三角主單元轉化為正方形單位單元,由此的到轉化關系[6]
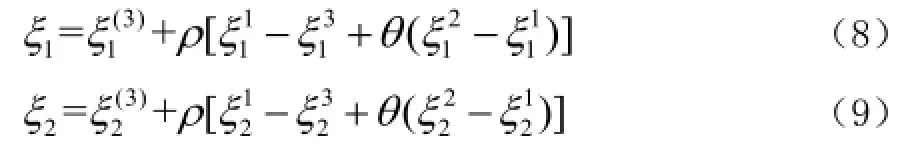
由上式帶入圖坐標點可得

變換后的得到的雅克比


圖1 廣義極坐標變換
3 脈動求輻射聲場驗證
脈動球源是指隨時間在進行均勻振動的球體,表面做簡諧振動,脈動求向它存在的聲場輻射聲壓,滿足本文假設條件,輻射聲場聲壓可以通過解析公式計算解析解,作為驗證邊界元法的一種有效手段,與邊界元法計算得到的數值解進行對比,驗證邊界元法的有效性。
對脈動球半徑r0=0.5(m),介質密度ρ0=1.21kg/m3,脈動求表面振動速度ua=1m/s建兩種單元模型,脈動球聲場輻射聲壓解析解計算公式有
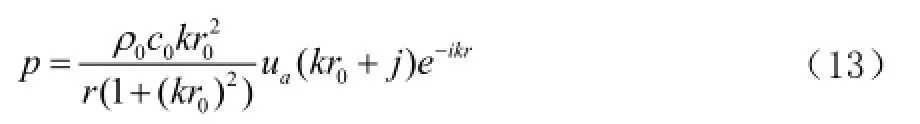
對脈動球邊界離散采用四邊形網格,選用兩種網格尺寸,得到場點網格,第一種為四邊形網格單元,單元尺寸為50mm,節點數為1269,單元數為1267,第二種為單元尺寸30mm,節點數和網格數分別為3164、3162,對比網格質量提高后對計算聲場聲壓精度的影響。
由于Fortran語言計算速度較快,適合大型程序開發與維護,針對大型計算問題,可以將模型分配幾種情況單獨計算,這樣可以縮減計算時間,本文邊界元積分方程程序采Fortran語言編寫。
對于脈動球場聲壓本文分別計算不同場點和不同頻率下聲壓進行對比,表1為場點網格1對應的不同頻率下場點聲壓解析解和數值解對比結果,從表可以的得出,在低頻段,解析解與數值解吻合較好,當頻率升高后,數值解相應誤差增加。
表2為場點網格2對應解析解與數值解對別結果,與表3變化趨勢類似,隨頻率增加后聲壓幅值誤差有所增加,對比表1,在頻率700Hz以上,計算效果明顯改善,分析原因由于脈動球建模劃分網格質量原因造成表4結果更近解析解。
以上結果分別對比了不同網格不同頻率對比結果,表3為網格1計算的到不同場點聲壓對比結果,頻率為50Hz,不同場點得到的聲壓在低頻情況邊界元法計算得到的數值結果與解析結果誤差較小,并且場點與脈動球源距離變化后誤差并沒有明顯變
表4為在1500Hz頻率下計算場點聲壓結果對比,當頻率升高后,場點聲壓解析解與數值解仍相差較小,誤差在1%以下,滿足工程應用需要。
對于兩種網格,計算時間也有所區別,網格1節點較少,單元較少,而網格2節點數和單元數為網格1的2.5倍,兩種網格計算時間分別為277.479 (s)、1568.574(s),網格2的計算時間是1的5.65倍,嚴重增加了計算時間。
4 結論
場點聲壓隨頻率變化數值解與解析解吻合較好,當頻率增加聲壓略微產生波動。場點與脈動球距離變化不大時,聲壓誤差沒有明顯變化。
網格質量提高后對聲場聲壓預測低頻精度沒有明顯提高,高頻誤差減小,但計算時間數倍增長。
存在誤差可能原因是在離散邊界是認為邊界單元為平面單元,造成誤差。在計算過程中考慮到實際問題不可能將邊界離散很多單元,所以本文離散邊界單元較大,也造成誤差。但這不影響對實際問題的分析。

表1 網格1不同頻率對比結果

表2 網格2不同頻率對比結果

表3 網格1場點聲壓結果

表4 網格2場點聲壓結果
[1]高貴兵,張道兵,岳文輝,等.一種具有唯一解的邊界元法計算三維聲散射問題[J].機械科學與技術,2013,32(8):1172-1175.
[2]郭偉,蔡明,馬俊.聲輻射邊界元數值計算[J].船海工程2011,40(1):101-103.
[3]黎勝,趙德有.用邊界元法計算結構振動輻射聲場[J],大連理工大學學報,2000,40(4):391-394.
[4]杜功煥,朱哲民,龔秀芬.聲學基礎[M].南京:南京大學出版社.
[5]Ursell F. On the exterior problems of acoustics[C]//Mathematical Proceedings of the Cambridge Philosophical Society. Cambridge University Press, 1973, 74(01): 117-125.
[6] Boundary element acoustics: Fundamentals and computer codes[M]. Wit Pr/Computational Mechanics,2000.
O29
A
1674-6708(2015)145-0113-02

