一類廣告擴散模型的Hopf分岔分析

2015-12-29 08:59:20丁學利

丁學利

（阜陽職業技術學院基礎教學部，安徽阜陽 236031）

1 引言

對分岔問題的研究可以追溯到十八世紀,人們對天體力學、流體力學、彈性力學和非線性振動中的一些失穩現象的探討，因此分岔問題有著深刻的應用背景.目前在物理學、化學、生物學、工程技術以及經濟學和社會學中都有著廣泛的應用[1,2].

Hopf分岔是一類很重要的分岔問題，它不僅有著重要的理論價值，而且在實際問題中有著廣泛的應用.本文利用分岔理論詳細討論了一類廣告擴散模型平衡點的穩定性和Hopf分岔，并且給出了發生Hopf分岔的參數條件，最后數值仿真驗證了理論推導的正確性.這對研究廣告擴散模型的實際應用，提供了理論依據.

考慮如下的廣告擴散模型[3,4]：

其中β，ε，k均為正常數，設置 α 為分岔參數.系統（1）有唯一的平衡點，在平衡點E0處的Jacobian矩陣為

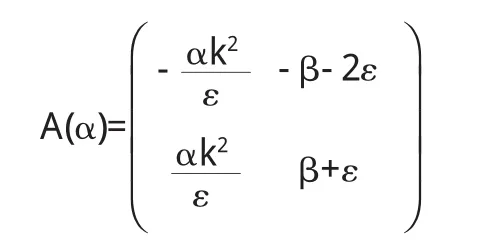
其特征方程為

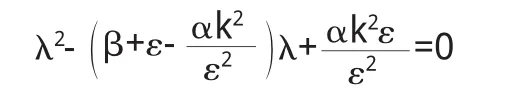
即 λ2-trA(α)λ+detA(α)=0，因此令 μ(α0)=0，得

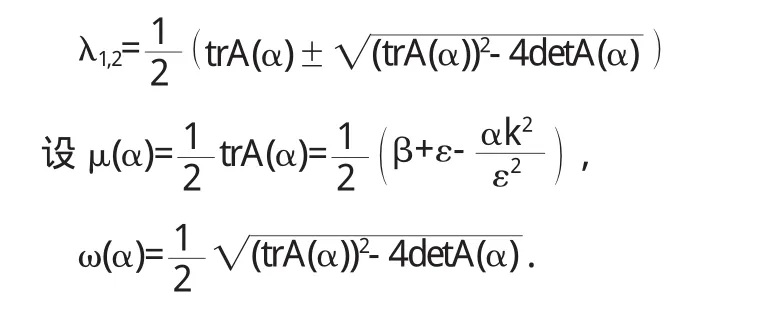
且 ω2(α0)=detA(α0)=(β+ε)ε>0.

定理 1 （1）當 α>α0時，若(trA(α))2-4detA(α)>0(<0)，則特征方程的根為兩個相異的負實根（一對具有負實部的共軛復根），從而系統（1）的平衡點是穩定的結點；

（2）當 0<α<α0時，若(trA(α))2-4retA(α)>0(<0)，則特征方程的根為兩個相異的正實根（一對具有正實部的共軛復根），從而系統（1）的平衡點是不穩定的焦點，即有可能發生Hopf分岔.

定理 2 當0<α<α0時，系統（1）發生Hopf分岔.

證明根據文獻[3]，只需要驗證兩個條件，即μ'(α0)≠0（橫截條件）和 l1(α0)≠0(非退化條件為第一李雅普諾夫系數）.

首先橫截條件很容易證明：

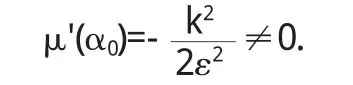
下面計算第一李雅普諾夫系數.

在α=α0處，平衡點E0的坐標為

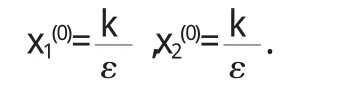
作坐標變換

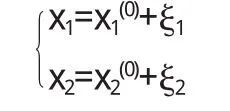
這樣就把平衡點E0變到坐標原點，系統（1）化成：

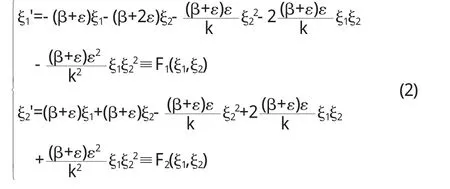
系統（2）可表示為下面的形式：

其中A=A(α0)，多線性函數B和C'是關于平面向量ξ=(ξ1,ξ2)T，η=(η1,η2)T，ζ=(ζ1,ζ2)T的函數，其值為

滿足 Aq=iωq，ATq=-iωq，且〈p,q〉=1.

第一李雅普諾夫系數為

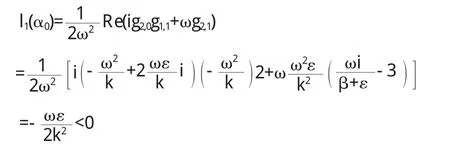
其中

所以滿足非退化條件 l1(α0)≠0.因此，在 0<α<α0處發生Hopf分岔，產生穩定的極限環.由于l1(α0)<0，所以是超臨界Hopf分岔.

下面我們將用Matcont軟件來分析廣告擴散模型的動力學行為，其參數使用為β=0.5，ε=k=9.5，α為分岔參數.

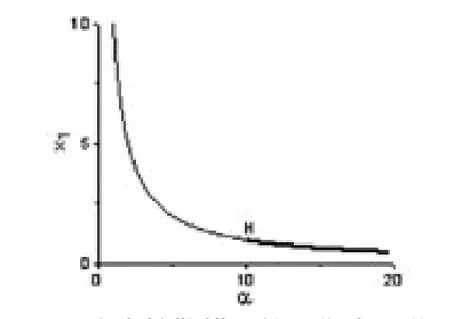
圖1 廣告擴散模型的平衡點分岔圖

圖1是廣告擴散模型的平衡點分岔圖，粗實線表示穩定的結點，細實線表示不穩定的焦點，H表示Hopf分岔點，此時α0=10是發生Hopf分岔的臨界點.

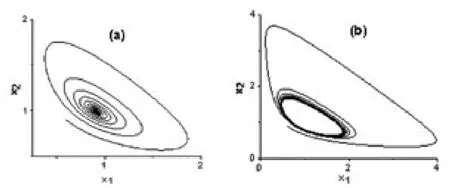
圖2 廣告擴散模型的相圖.（a）α=11>α0；（b）α=9.5<α0

圖2是廣告擴散模型的相圖.當α=11>α0時，系統的平衡點是漸進穩定的（圖 2（a））；當 α=9.5<α0時，系統產生穩定的極限環（圖 2（b）），即發生了 Hopf分岔.

本文對廣告擴散模型平衡點的穩定性進行了研究，并且證明了系統發生Hopf分岔的參數條件.結果表明在一定條件下，系統發生Hopf分岔是超臨界的.最后，數值仿真驗證了理論推導的正確性.此外，系統還有一些性質需要進一步的分析，如極限環如何消失，是否發生同宿軌分岔，以及能否出現混沌等.

〔1〕劉秉正，彭建華.非線性動力學[M].北京：高等教育出版社，2004.

〔2〕張琪昌，王洪禮,等.分岔與混沌理論及應用[M].天津：天津大學出版社，2005.

〔3〕KUZNETSOV.Yuri A.Elements of applied bifurcation theory[M].New York:Springer,1997.

〔4〕FEICHTINGER.G.Chaotic behavior in an advertising diffusion model[J].Internation Journal of Bifurcation and Chaos:1995.