開孔有限平板應力集中問題的有限元分析

譚　林，郭　原

(重慶大學 航空航天學院，重慶　400044)

開孔有限平板應力集中問題的有限元分析

譚林，郭原

(重慶大學 航空航天學院，重慶400044)

摘要：針對中心帶有圓孔的有限寬平板的應力集中問題，利用軟件ABAQUS對其進行有限元分析。定義了孔邊應力集中系數K和描述板寬與孔徑相對尺度的特征參數ξ，研究得到了反映不同板寬下孔邊應力集中程度的ξ-K關系曲線圖，并將其與無限大板寬情形下的解析解進行比較，給出解析解的適用范圍。在此基礎上，數值分析了不同形狀的橢圓孔口應力集中問題，并對橢圓尖端奇異性進行簡要討論。

關鍵詞：開孔有限平板；應力集中；圓孔；橢圓孔；相對尺度

開孔構件在機械、車輛、土木以及航空航天等工程領域中有著廣泛應用。由于開孔，孔口附近的應力遠大于無孔時的應力，也遠大于距離孔口較遠處的應力，這種現象被稱為“孔邊應力集中”[1]。由于孔邊的應力水平較高，開孔構件在承受較小載荷時，孔邊應力集中區域很可能已經產生塑性變形。尤其是當零件受周期性變化的應力或受沖擊載荷作用時，應力集中對零件的強度有嚴重影響，往往是零件破壞的根源[2]。因此，開孔構件的應力集中問題是工程設計中的關鍵問題之一。

工程上通常定義孔邊最大應力與板件遠場應力之比為應力集中系數，用以表征應力集中的程度。應力集中系數與孔的形狀有關[3]。一般而言，圓孔的應力集中程度相對較低，在結構設計中應對其優先考慮。此外，考慮到具有尖角的孔口在尖角處會發生高度的應力集中，工程中通常用近似于圓形的孔——橢圓孔予以代替。因此，研究帶有不同形狀的橢圓孔口的平板應力集中問題具有一定的工程應用價值。此外，帶孔平板應力集中問題作為彈性力學中的經典問題，自德國的G.Kirsch首先得出圓孔附近的應力分布結果以來，引起了眾多中外學者的廣泛關注[4-6]。但他們多采用彈性力學基本理論，借助復變函數和保角變換等數學方法，進而求得無限大板寬的孔邊應力分布的解析解。但工程中的構件常常不能當作“無限大”來處理，而孔邊應力集中系數又會隨著板寬的不同而發生顯著改變，故較為準確地求解帶孔有限寬平板的應力集中問題尤為重要。

本文利用有限元軟件ABAQUS，對受單軸均布拉伸載荷作用下的有限寬中心圓孔板進行有限元分析，并研究不同板寬對孔邊應力集中系數的影響。在此基礎上，探討了固定板寬下，中心帶有不同形狀的橢圓孔口(即不同的長、短半軸)的平板應力集中問題，并與解析解進行比較。

1基于ABAQUS的開圓孔有限平板應力集中問題研究

1.1　開圓孔無限大平板孔邊應力集中問題的理論解答

圓孔應力集中問題的力學模型如圖1所示：一個x方向承受均布載荷q的板寬為L的正方形平板，板中有半徑為r的小圓孔，平板厚度遠小于其寬度。

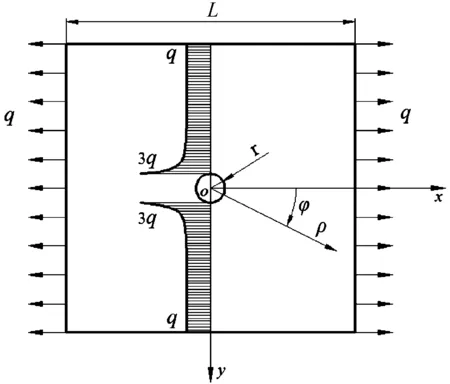
圖1　帶圓孔平板力學模型

由于小圓孔的存在，平板內的應力分布必然會受到影響，但根據圣維南原理，這種影響僅局限于孔的附近區域，在距離孔邊的較遠處，此影響顯著減小。故在經典彈性力學理論中，當平板寬度遠遠大于小孔半徑時，可得如下基爾斯解答[1,7]：

(1)

沿著y軸，即當φ=90°時，環向正應力為

(2)

(3)

稱為應力集中系數(stressconcentrationfactor)，本文K=3。

1.2　基于ABAQUS的不同板寬的圓孔孔邊應力集中問題研究

在工程實際中，有限板寬下的孔口應力集中問題可借助有限元軟件ABAQUS得到近似解答。平板材料采用高純度鎳[8-10]，其彈性模量E=207 000MPa，泊松比ν=0.312。對于圖1所示的力學模型，考慮到平板厚度遠遠小于板寬，故可將其視為平面應力問題。而基于結構和載荷的對稱性，只需取模型的1/4進行分析。邊界條件設定為：x=0，ux=0；y=0，uy=0。平板右端所受均布載荷q=2MPa。由于孔邊附近會出現應力集中，為了保證計算精度，對靠近孔邊的局部區域需細化網格，如圖2所示。

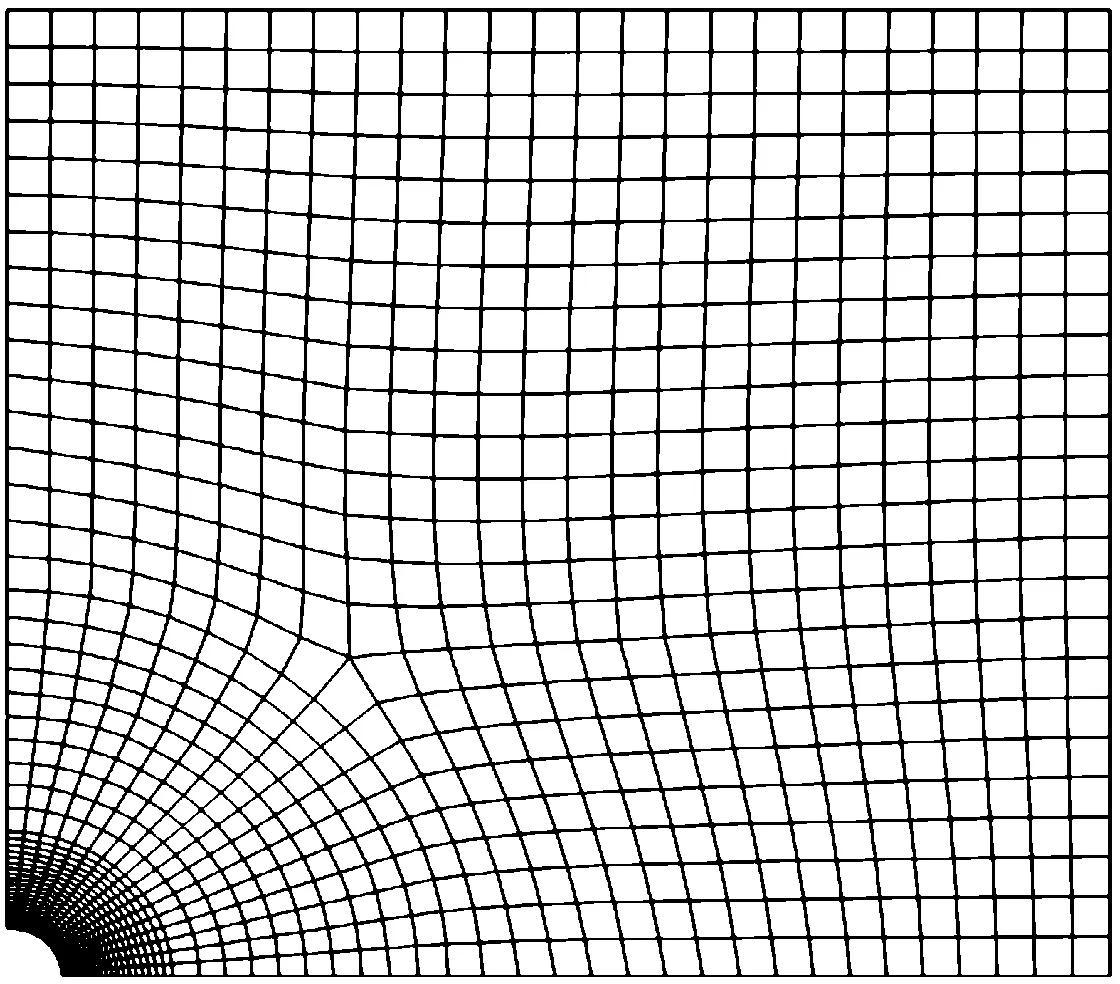
圖2　孔邊附近細化網格

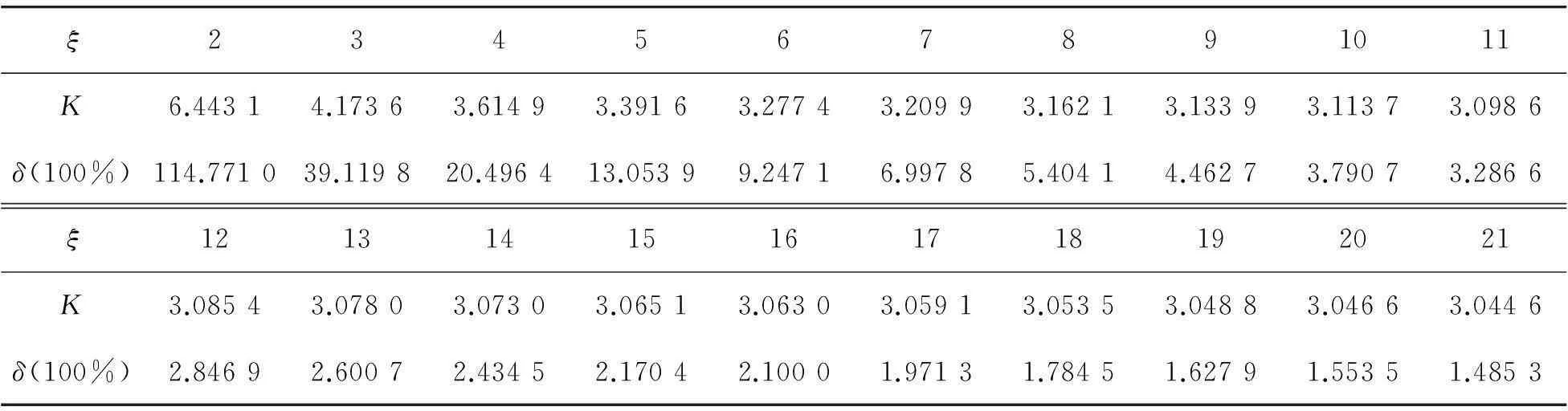
表1　ξ-K關系表

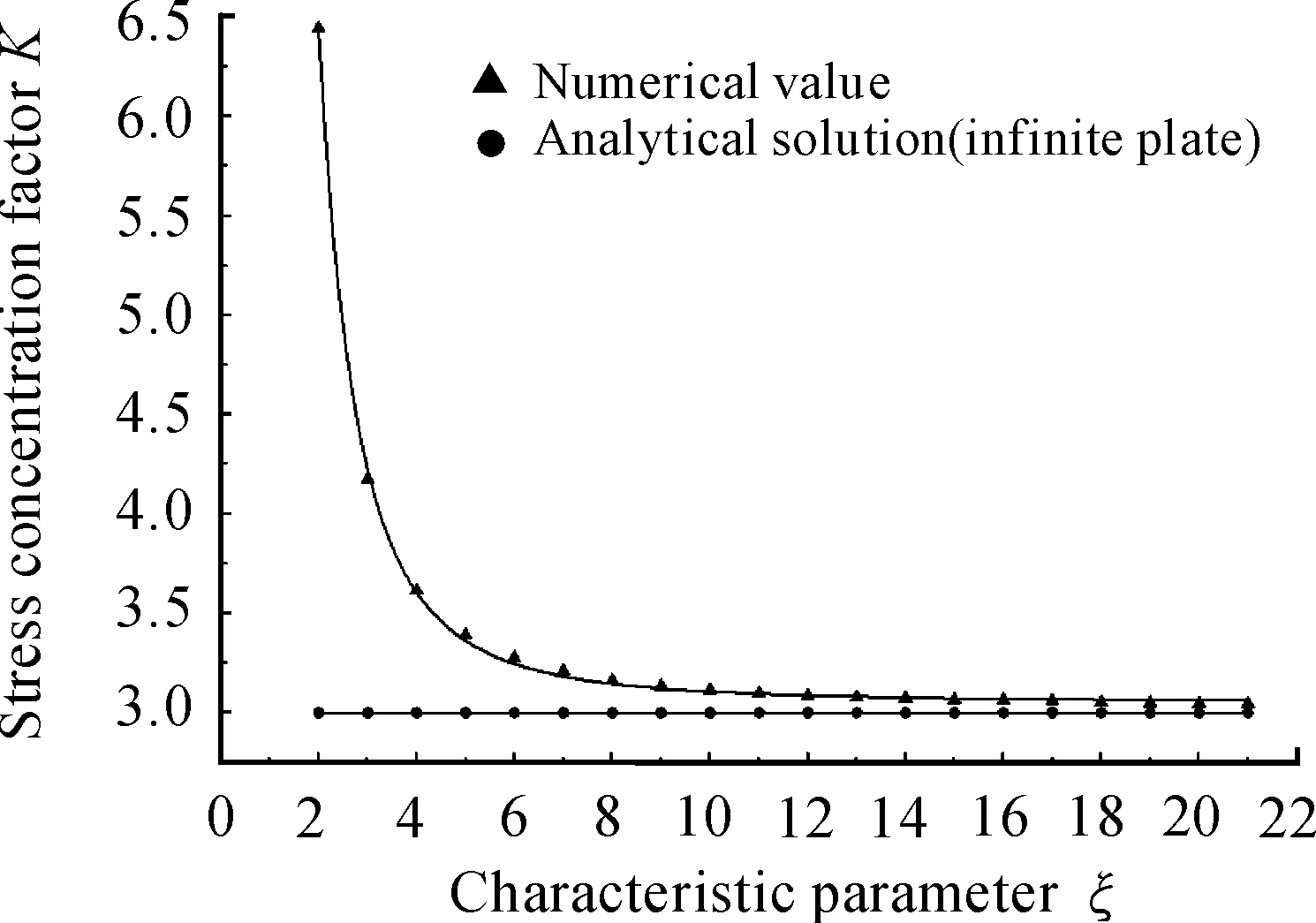
圖3　ξ-K關系曲線

分析表1和圖3可知：當ξ≤8時，孔邊應力的分布情況受到邊界條件的影響，相對誤差較大(最大已超過114.77%)。此時，由于開孔而減少的截面尺寸等因素也會對應力值產生較大影響，已不能稱其為“小孔口問題”，但K會隨著ξ的增大而迅速減小。當ξ≥9時，隨著ξ的繼續增大，K繼續緩慢減小直至趨近于解析值3。若按照工程中常用的相對誤差小于5%的標準考慮，則此時有限寬帶孔平板的孔邊應力集中問題可作為無限寬帶孔平板近似處理。此外，不妨考察當ξ=20時，平板的應力分布情況，如圖4所示。由x方向的應力云圖可知，其應力分布主要有2個明顯特點：一是集中性，孔口附近應力遠大于較遠處應力，且應力最值發生在孔邊上；二是局部性，由于小孔引起的應力擾動，主要發生在距離孔邊1.5d的局部范圍內[1]。這些特點和前文所述的此問題的理論分析吻合較好，從側面論證了本文所建立的有限元計算模型具有較好的適用性及合理性。

圖4　平板σx的應力分布(ξ=20)

2基于ABAQUS的開橢圓孔有限平板應力集中問題研究

考慮到帶有橢圓形孔口的構件在工程中被廣泛應用，而其應力集中程度受到橢圓孔口形狀的影響較大。因此，有必要進一步探討單軸均拉作用下的帶有橢圓孔口的平板應力集中問題。現考慮如圖5所示的力學模型，其中a，b分別為橢圓的長、短半軸。在彈性力學中，借助復變函數和保角變換等數學方法，可求得帶橢圓孔平板的應力分布情況，而且最大周向拉應力出現在橢圓長軸的兩端，橢圓孔口的應力集中系數為[11]：

(4)

結合前文相關研究，出于控制變量的考慮，將板寬L固定為40 mm，長軸2a定為2 mm。另外，平板材料、單元類型以及均布載荷等工況與圓孔問題保持一致。現基于ABAQUS軟件平臺，有規律地改變b，分析對應于不同b/a情況下的平板應力分布情況，求得相應的K值，將其與解析解進行比較并計算其相對誤差，詳見表2和圖6。

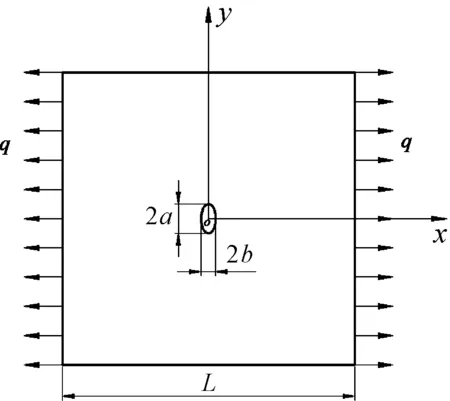
圖5　帶橢圓孔平板力學模型

圖6　b/a-K關系曲線

b/a0.10.20.30.40.50.60.70.80.91K-解析解21117.6667654.33333.85713.53.22223K-數值解15.60569.47697.32965.97605.06574.41353.93453.57053.28483.0466δ(100%)25.687713.84634.39700.40031.31471.84912.00432.01371.94171.5535

由表2與圖6可知：橢圓孔口應力集中系數隨著短軸b的增大而減小，直至b=a時(即橢圓的特殊情況——圓孔)，K趨近于3。觀察其相對誤差，當 b/a≥0.3時，兩者吻合較好(誤差均在5%以內)；但當b/a<0.3時，誤差較大。其原因大于，隨著b的不斷減小，在橢圓長軸兩端會逐漸出現幾何奇異性，進而導致橢圓尖端的高度應力集中，采用的常規單元已經不能較準確地反映橢圓尖端的奇異性。因此，為得到可靠的結果，尖端的網格必須劃分得足夠細(網格尺寸通常為(10-2~10-3)×2a)，或者采用諸如奇異元素法、匯聚參數法等特殊有限元法[12]。

3結論

1) 利用有限元軟件ABAQUS，對受單軸均布拉伸載荷作用下的有限寬中心圓孔板進行數值分析，研究了應力集中系數K隨特征參數ξ的變化規律，并將其與解析解比較得出(詳見表1和圖3)：當ξ≤8時，K會急劇增大；當ξ≥9時，K會隨著ξ的繼續增大而緩慢減小直至趨近于解析值3，其相對誤差均在5%以內。即在工程實際中，只有當ξ≥9時，有限板寬的孔邊應力集中系數才可用無限大板寬下的解析解近似代替。

2) 基于ABAQUS，進一步探討了中心帶有橢圓孔口的平板應力集中問題，數值驗證了孔邊應力集中系數K與橢圓短、長半軸之比b/a之間的關系(詳見表2與圖6)，并將其與解析解比較得出：當b/a≥0.3時，兩者吻合得較好；當b/a<0.3時，誤差較大，即此時再用常規單元已不能較準確地反映橢圓尖端的奇異性。

3) 本文的研究為工程中開孔構件的設計及其力學分析提供一定的參考。值得注意的是：由于本文考慮的是帶孔薄板(厚度遠小于板寬)，故可將其視作平面應力問題處理。在工程中，當沿厚度方向上的應力變化不可忽略時，宜采用三維有限元模型以得到更為精確的結果[13]。另外，若令橢圓的短半軸b趨于零，橢圓孔口則退化為長度為2a的穿透型裂紋，此時裂紋尖端的應力分布將是理論和工程研究的重點[14-16]。

參考文獻：

[1]徐芝綸.彈性力學簡明教程[M].3版.北京:高等教育出版社，2002.

[2]劉鴻文.材料力學[M].4版.北京：高等教育出版社，2004.

[3]航空工業部科學技術委員會.應力集中系數手冊[M].北京：高等教育出版社，1990.

[4]Inglis C E.Stresses in a plate due to the presence of cracks and sharp corners[J].Trans.Roy.Inst.Naval Arch.，1913，66:219-230.

[5]Darwish F，Gharaibeh M，Tashtoush G.A modified equation for the stress concentration factor in countersunk holes[J].European Journal of Mechanics A/Solids，2012，36:94-103.

[6]羅林，向宇，王啟智.拉伸偏心橢圓孔板的應力集中系數表達式[J].應用數學和力學，2012，33(1):113-124.

[7]吳家龍.彈性力學[M].北京:高等教育出版社，2001.

[8]李雷，謝水生，黃國杰.應變梯度塑性理論下超薄梁彎曲中尺度效應的數值研究[J].工程力學，2006，23(3):44-48.

[9]Stolken J S，Evans A G.A microbend test method for measuring the plasticity length scale[J].Acta Mater，1998，46:5109-5115.

[10]成大先.機械設計手冊[M].5版.北京：化學工業出版社，2010.

[11]卓衛東.應用彈塑性力學[M].2版北京：科學出版社，2013.

[12]酈正能.應用斷裂力學[M].北京：北京航空航天大學出版社，2012.

[13]佘崇民，郭萬林，孟波，等.橢圓孔三維應力集中及其對疲勞強度的影響[J].計算力學學報，2007，24(2):215-218.

[14]王發穩，尹明德，呂倩.基于ABAQUS的貨叉三維裂紋應力強度因子有限元分析[J].機械工程與自動化，2014，(3):12-15.

[15]陳帥，于存貴，李宗濤，等.ABAQUS 子程序 UAMP 的應用[J].四川兵工學報，2014，35(1):149-152.

[16]王立清.工程中含接觸問題的孔邊裂紋應力強度因子數值研究[D].哈爾濱：哈爾濱工業大學，2009.

(責任編輯劉舸)

收稿日期：2015-03-16

基金項目：國家自然科學基金資助項目(11372365)；煤礦災害動力學與控制國家重點實驗室自主研究課題重點項目(2011DA105287-ZD201403)

作者簡介：譚林(1990—)，男，重慶萬州人，碩士研究生，主要從事結構振動與控制、沖擊動力學研究。

doi:10.3969/j.issn.1674-8425(z).2015.07.006

中圖分類號：O343.4

文獻標識碼：A

文章編號：1674-8425(2015)07-0035-05

FiniteElementAnalysisofFinitePlatesfor
StressConcentrationofHoles

TANLin,GUOYuan

(CollegeofAerospaceEngineering,ChongqingUniversity,Chongqing400044,China)

Abstract:The stress concentration problem of finite-width plates with a central circular hole were analyzed in terms of finite element method by ABAQUS software. We defined the stress concentration factor K and characteristic parameter ξ used to describe the relative scale between the width of plates and the diameter of the circular hole. By means of a series of numerical experiments, the ξ-K curve was obtained to reflect the stress concentration level around the hole and then compared with the analytical solution to get its scope of application. In addition, the stress concentration phenomena of elliptic holes with various shapes were numerical analyzed. Besides, the singularity of elliptic tip was discussed briefly.

Key words:finite plates with holes; stress concentration; circular hole; elliptic hole; relative scale

引用格式：譚林，郭原.開孔有限平板應力集中問題的有限元分析[J].重慶理工大學學報：自然科學版，2015(7):35-39.

Citationformat：TANLin,GUOYuan.FiniteElementAnalysisofFinitePlatesforStressConcentrationofHoles[J].JournalofChongqingUniversityofTechnology:NaturalScience，2015(7):35-39.